切比雪夫多项式的数字预失真算法及其FPGA实现

袁江南

(厦门理工学院光电与通信工程学院，福建 厦门 361024)



切比雪夫多项式的数字预失真算法及其FPGA实现

袁江南

(厦门理工学院光电与通信工程学院，福建 厦门 361024)

将切比雪夫多项式引入到数字预失真器的设计中，利用其特有的递归生成特性，提出了一种奇偶阶分离的生成方法，避免了高阶幂次操作并节约了资源．仿真表明，切比雪夫多项式预失真器的效果和收敛性能均优于现有的普通以及正交多项式．在现场可编程门阵列(field-programmable gate array,FPGA)上实现了设计，经过定点仿真验证，所设计的预失真器可以有效地抑制带外频谱泄漏，邻道泄漏比(adjacent channel leakage radio, ACLR )比普通记忆多项式有5～10 dB的提升．

数字预失真；切比雪夫多项式；记忆多项式；FPGA

为了提高频谱效率，现代通信系统广泛采用多进制、多载波等高峰均比调制技术．高峰均比信号进入射频功率放大器的饱和区将产生带外频谱泄漏问题，导致ACLR性能下降[1]．若降低功率放大器的静态工作点，避免信号进入饱和区，则其效率将会大大降低．针对这一问题，目前通行的做法是在数字基带部分设置自适应数字预失真器，以期对功率放大器的非线性特性进行补偿．在数字预失真技术中，基于多项式的方法收敛速度快且易于实现记忆特性，从而获得了广泛的应用[2]．然而，多项式预失真器要求对数据进行幂次操作，阶数较高时数据矩阵的条件数增长过快，容易带来数值稳定性问题[3]，算法的收敛速度和辨识精度无法保证．运用正交多项式设计预失真器可以有效地解决这一问题．

目前，有关正交多项式的文献比较偏重正交多项式的提出以及正交性的证明[4-5]，实际的工程应用和定点性能研究鲜有报道．文献[4-5]所提的正交多项式可以在阶数较高时仍保持较小的条件数，但是其生成比较困难，不便于工程应用．相比之下，切比雪夫多项式具有性能优越、形式简单、可递归生成等优点，且便于实现工程应用．因此，本文首先对各种多项式的条件数以及预失真器的性能进行了仿真比较；然后提出了奇偶阶分离的实现方法．定点性能仿真表明，所提的设计方法预失真效果优于现有的多项式，而且具有硬件资源占用率低的优点，便于工程应用.

1　正交多项式数字预失真算法

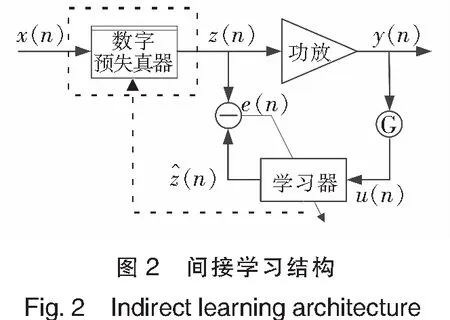
数字预失真原理如图1所示，如果预失真器的非线性特性与功率放大器(简称功放)互逆，则合成系统将呈现线性特性．目前，实用的预失真器一般使用间接学习结构自适应调节其参数，如图2所示．

(1)

(2)

正交多项式预失真器的前向和反馈通道均使用ψk(u(n))进行预失真运算和参数辨识，从而解决了相关矩阵条件数过大的问题．但式(2)仅对某种特定概率分布的数据成立，如果数据的概率分布稍偏离预期，正交性便难以保证，例如文献[4]提出的正交多项式针对的是均匀分布的数据．通常高峰均比的通信信号经过峰值限制操作后服从某种亚高斯分布．在实际运用时，并不要求式(2)严格成立，只要求尽可能缩小相关矩阵的条件数即可[4]．

2　切比雪夫多项式预失真算法

切比雪夫多项式是一种常用的正交多项式[7]，其各阶之间可以借助递推公式生成：

(3)

与式(1)对应，式(3)中仅k为奇数的各阶用于构建预失真器．图3是各种多项式数据自相关矩阵的条件数比较．

从图3(a)可以看出，均匀分布正交多项式在均匀分布信号输入的情况下优势比较明显，而在图3(b)中4载波WCDMA信号输入的情况下，切比雪夫多项式的条件数要小于均匀分布多项式．图3(c)中的普通记忆多项式无论在何种输入的情况下其条件数增长都非常迅速．

图4是采用LMS算法辨识预失真器参数后的预失真效果和算法收敛速度和精度的比较．仿真时预失真器的阶数为7．LMS算法的性能虽不如最小二乘算法，却具有计算简单、易于工程实现的优点[8]．可见，切比雪夫多项式预失真器的收敛速度、精度以及频谱扩展抑制效果均略优于均匀分布多项式．

3　切比雪夫多项式预失真器的设计与实现

近年来，随着28 nm FPGA投入使用，FPGA在通信设备中获得了广泛的应用[9]．赛灵思公司的System Generator工具基于Simulink仿真平台，便于进行算法定点实现过程中的信号剪裁、位宽确定、溢出控制等操作，最终的仿真模型可以直接生成硬件码流并下载实现．

由于定点算法的位宽是有限的，通信信号的动态范围又比较大，小信号经过高阶幂次操作以后近似为零，这将影响预失真器的效果．切比雪夫多项式中包含了各阶普通多项式，其值在一定幅度范围内反复振荡，并不会随着阶数的升高缩减为零，但需要消耗较多的硬件资源．本文利用切比雪夫多项式的特性，设计了一种奇偶价分离的生成方法．首先直接生成偶数阶，然后再利用递推公式生成奇数阶并构造预失真器．仔细观察切比雪夫多项式的各偶数阶，将其因式分解后可以发现，其偶阶之间存在着直接递推规律，如表1所示．

表1　切比雪夫多项式的偶数阶递推关系

如果直接按照切比雪夫多项式的表达式实现，仍然需要对数据进行高阶幂次操作．而当输入模值在0～1之间时，表1中T2～T12各阶在-1～1之间变化，除此以外的最高幂次仅为平方，且包含了公共因子，可以较大幅度地节约硬件资源．获得偶数阶以后，从T1=x开始，其余奇数阶可由式(3)得到，并用于构造预失真器．

图5是使用System Generator实现的7阶切比雪夫多项式预失真器整体结构图，预失真器的记忆深度为3．图5(b)是第6阶切比雪夫多项式内部结构，其中乘4、2等操作可以利用移位实现，从而节约乘法器的使用．最终在赛灵思7序列FPGA中的Artix序列xc7a200tfbg676-2器件实现了设计．布线后时序分析结果表明，设计可以工作在500 MHz以上的时钟频率．表2是奇偶分离法和直接按照切比雪夫各阶表达式实现方法的资源占用比较．由表2可知，本文的奇偶分离实现方法可相对节约52%的信号处理单元的使用量．

表2　布局布线后资源占用比较

资源名称奇偶分离法占用数比例/%直接实现法占用数比例/%资源总数触发器(FF)561561267600查找表(LUT)7666692326.9133800数字信号处理单元(DSP48)841112817.3 740

图6是记忆多项式和切比雪夫多项式预失真效果的定点仿真比较结果．为了提高辨识精度，预失真器参数辨识采用最小二乘算法[10]．从图6(a)中可以看出，记忆多项式预失真器在9阶以后效果基本上达到极限，13阶效果反而比11阶下降．这时由于数值较小的定点数在高阶幂次操作以后缩减为零．定点实现的切比雪夫多项式预失真效果在阶数逐步提高以后性能仍有改善，相比于普通记忆多项式，在不同的频带内ACLR各有5～10 dB的优势．

4　结论

切比雪夫多项式预失真器的带外抑制效果，以及预失真器参数辨识的精度和收敛速度等性能均优于现有的普通和正交多项式，其特有的递归生成特性还有利于预失真器的硬件实现．奇偶阶分离递推的方法可以避免数据直接高阶幂次操作，有利于节约资源，提升性能．硬件设计工具的定点仿真验证表明，相比于普通记忆多项式，切比雪夫多项式预失真器的ACLR性能有5～10 dB的提升．所设计的预失真器可在赛灵思7序列FPGA上实现，下一步研究工作将在硬件平台上测试预失真器的性能．

[1]钟佩琳,王红星,孙小东，等.基于压缩量化的非正弦时域正交调制信号预失真方法[J].电子与信息学报,2013,35(3):658-664.

[2]李波,葛建华,王勇.一种新的分数阶记忆多项式预失真器[J].电子与信息学报,2009,31(8):1 961-1 964.

[3]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

[4]RAICH R,HUA Q,ZHOU G T.Orthogonal polynomials for power amplifier modeling and predistorter design[J].IEEE Transactions on Vehicular Technology,2004,53(5):1 468-1 479.

[5]何华明,唐亮,张春生，等.一种基于正交多项式的自适应预失真方法[J].计算机应用与软件,2013,30(4):97-100.

[6]DING L,ZHOU G T，MORGAN D R.A robust digital baseband predistorter constructed using memory polynomials[J].IEEE Transactions on Communications,2004,52(1):156-162．

[7]MATHEWS J H ,FINK K D.数值方法[M].周璐，陈渝，钱方，译.北京:电子工业出版社，2005.

[8]HAYKIN S.自适应滤波器原理[M].郑宝玉，译.北京:电子工业出版社,2006.

[9]孟宪元,陈彰林,陆佳华.Xilinx新一代FPGA设计套件Vivado应用指南[M].北京:清华大学出版社,2014.

[10]MORGAN D R,MA Z X， KIM J Y， et al.A generalized memory polynomial model for digital predistortion of RF power amplifiers[J].IEEE Transactions on Signal Processing,2006,54(10):3 852-3 860.

(责任编辑雨松)

Digital Predistortion Algorithm Based on ChebyshevPolynomials and its FPGA Implementation

YUAN Jiangnan

(School of Optoelectronic & Communication Engineering,Xiamen University of Technology,Xiamen361024,China )

In this paper,Chebyshev polynomials were drawn into the design of digital predistorters.The recursion generation character was exploited and a generation method of odd even order separation presented, which avoids high order power operations and saves resources.Simulation shows that the effects and convergence performances of Chebyshev polynomials predistorter are superior to that of common and orthogonal polynomials now available.The design is implemented in field-programmable gate array(FPGA).Fix point simulation shows that the predistorter can effectively suppress out-band spectrum leakages.Its adjacent channel leakage radio(ACLR) performance is about 5～10 dB superior to that of memory polynomials.

digital predistortion;Chebyshev polynomials;memory polynomials;FPGA

2015-11-16

2015-12-10

福建省自然科学基金项目(2015J01670)；厦门理工学院高层次人才项目(YKJ14008R)；厦门市科技计划项目(3502Z20153017)

袁江南(1971-), 男,副教授,研究方向为通信信号处理及其VLSI实现.E-mail:jnyuan@xmut.edu.cn

TN713

A

1673-4432(2016)03-0052-05