一道2015年墨西哥数学奥林匹克试题的加强及推广

江苏省姜堰中等专业学校　(225500)

陈　宇



一道2015年墨西哥数学奥林匹克试题的加强及推广

江苏省姜堰中等专业学校(225500)

陈宇

2015年墨西哥数学奥林匹克一道不等式试题：

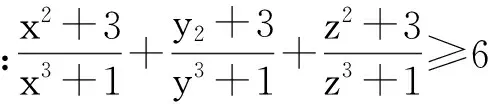
通过探究，笔者发现，沿用文[1]提供的证法，可以将该不等式加强并推广.

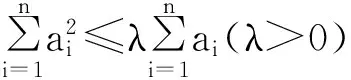
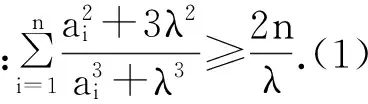
证明：首先给出预备定理：切比雪夫(Chebyshev)不等式(最初形式):

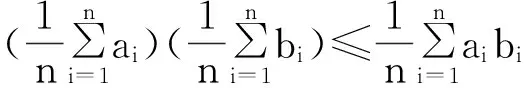
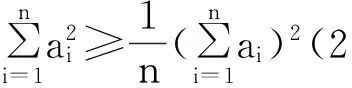
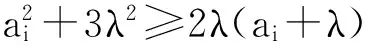
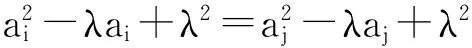
当n=3,λ>0时，令a1=x,a2=y,a3=z，不等式(1)即为原赛题加强式.即

已知x,y,z是满足x2+y2+z2≤λ(x+y+z)(λ>0)的正数.

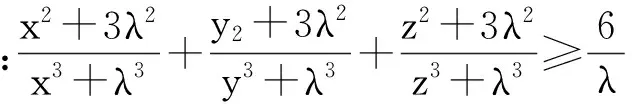
当n=3,λ=1时，令a1=x,a2=y,a3=z，不等式(1)即为原赛题.

[1]王文江.2015年国际数学奥林匹克不等式问题及解答集粹[J].中学数学研究(江西),2016,2.

[2]匡继昌.常用不等式(第四版)[M].山东科学技术出版社(77-79).