一道联赛题的视角转换

江苏省东台市安丰中学　(224221)

徐建华



一道联赛题的视角转换

江苏省东台市安丰中学(224221)

徐建华

1　试题简析

该题是2016全国高中数学联赛江苏初赛第9题，试题简洁朴实，内涵却很深刻，所涉及到的知识、方法十分丰富，而且条件等式的对称性，体现了数学美感，但也由于对称性，学生很容易利用x=y代入条件，解得x=y=2，从而猜想x+y的值只能是4，试题的信度不太很高，有点遗憾！当然，作为一个数学问题，它有很好的研究价值，能够锻炼学生的思维，拓展学生的知识面.

2　初步思考

权方和不等式的特殊情况与柯西不等式是相通的，所以方法2与方法1接近.这道题用排序不等式解决，也比较简洁.

3　视角转换

考试后，有学生问：老师，这道题我是用x=y代入条件，猜出结果x+y=4，严格求解怎么做？这个问题，还使笔者犯难了，参赛的是高二学生，他们没有参加过竞赛培训，还未选修“不等式”课，不知道柯西不等式等知识，上述三个方法，很难在短时间内与学生解释清楚，这促使笔者进一步思考，能不能转换视角，用学生现有的知识解决呢？

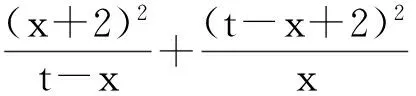
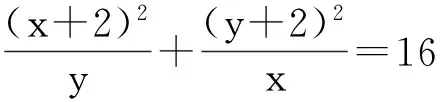
运算虽是繁了点，但对于知识缺乏的学生，却是有意义的思考，而且这里也体现了基本不等式的本质理解，“要用基本不等式，即要研究两个正数x,y的和与积的不等关系”，只要将条件转化为关于基本量x+y,xy的等式就行.而且，还给了笔者一个提醒，上述方程有解的思考，不应急于将y=t-x代入方程运算，先尽可能向x+y,xy上靠，最后再代入化简，可以简化运算，于是得到方法5.

解法5:同法4，得(x+y)3+4(x+y)2+4(x+y)=3xy(x+y+8)，令x+y=t，则y=t-x，所以t3+4t2+4t=3x(t-x)(t+8)，整理得关于x的一元二次方程3(t+8)x2-3(t+8)tx+t3+4t2+4t=0，所以Δ=9(t+8)2t2-12(t+8)(t3+4t2+4t)≥0，所以3(t+8)t-4(t2+4t+4)≥0，整理得t2-8t+16≤0，所以t=x+y=4.

4.试题改编

要真正解决这道题，还是需要学生思考的，但作为填空题，学生迅速猜出答案，失去思考的价值，区分度太低，没有信度.笔者认为，要么把它作为最简单的竞赛解答题，要么做点简单的改编.基于此，笔者把它改编成几道填空题，提高测试信度.

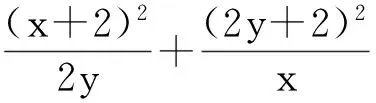
单墫先生曾讲过，不断地、持续地“思之、思之、思之、思之”，定有意想不到的收获.本文中，笔者就学生的疑问作了一点思考，虽没有什么大的发现，但深刻认识了这道简单联赛题的本质，得到了合理有效的多个处理方法.作为中学数学教师，我们要勤于思考，并要教会学生思考，这才是有意义的教学.如本文，教师若回答学生说，这道题要用到柯西不等式，中学阶段不学习，那学生只能望洋兴叹，数学太高深莫测了！反之，教师不急于回答学生，研究出方法4、5之后，再与学生交流研讨，最后说，如果我们到高三选修“不等式”，学习了柯西不等式、排序不等式等，这道题就有更完美的解答了，那就能激发学生的内在潜能了，将来定有很多学生选修“不等式”.