优选直线方程，减少解题长度

福建省闽清高级中学　(350800)

黄如炎



优选直线方程，减少解题长度

福建省闽清高级中学(350800)

黄如炎

直线与圆锥曲线的位置关系是高中平面解析几何的核心问题，是高考的重点，热点和难点．对直线与圆锥曲线的位置关系问题，教师们投入了成倍课时，设计了复习专题，强化了考试练习．学生们倾注了大量学时，经历了艰难思路，进行了繁杂运算，但教学效果却大失所望．主要原因是缺乏算理，导致大运算量使解题半途而废．除了数形结合，回归定义，设而不求，代标相减等方法可减少运算量外，还有影响运算量的一个很重要因素却被人们忽视了．在研究直线和圆锥曲线位置关系时，圆锥曲线方程相对确定，但直线方程的选择是多样的，若能根据题情选取最优直线方程，则可大大简化运算求解过程．

1.优选直线y=kx+b

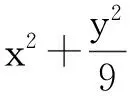
例1已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．

(Ⅰ)证明：直线OM斜率与l斜率乘积为定值．

对(Ⅰ)易证kOM·k=-9,(Ⅱ)解答如下．

解法1:(标准解答)设A(x1，y1)，B(x2，y2)，P(x0,y0)．四边形OAPB为平行四边形等价于AB、OP互相平分，即AB、OP中点重合，∴x1+x2=x0(1).

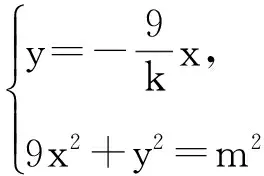
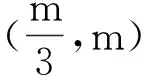
2.优选直线x=ky+b

在研究直线l与圆锥曲线位置关系时，若圆锥曲线方程中含x的项比含y的项简单(x只含一次项或x2系数比y2系数简单),则应选择直线方程为x=ky+b.

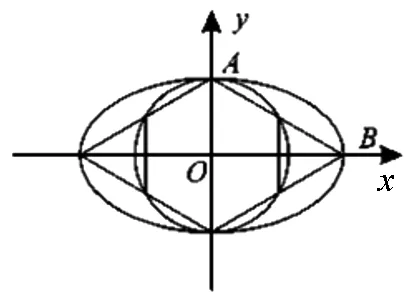
图1

(1)求椭圆M的方程；

(2)若直线l与圆O相切，且与椭圆M相交于P、Q两点，求|PQ|的最大值．

(2016年福建省高中毕业班质检理科数学第20题)

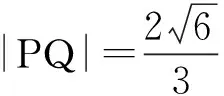
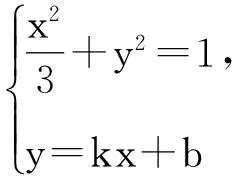
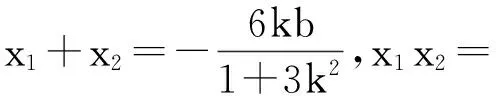
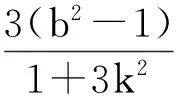
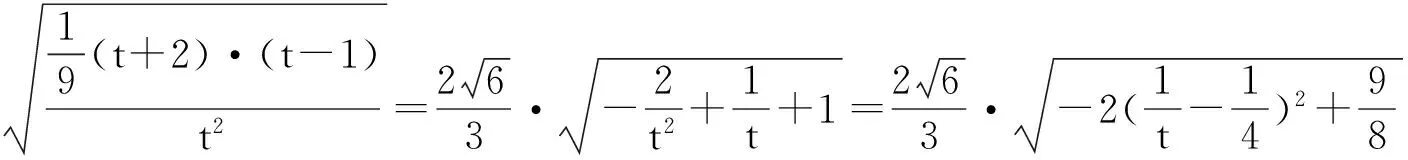
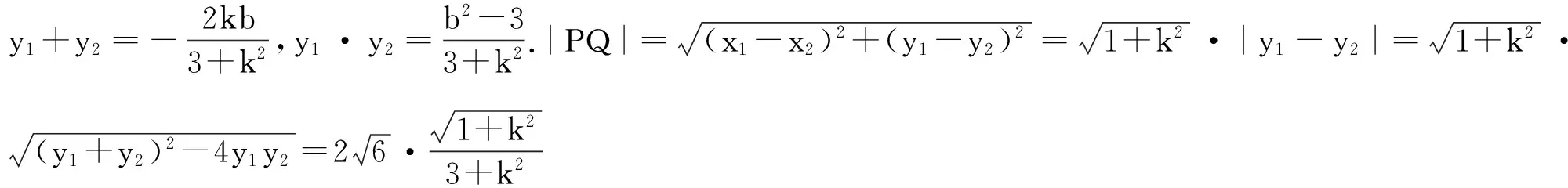
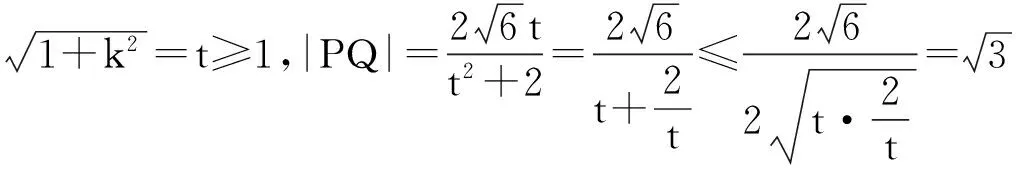
3.优选直线y=k(x-x0)+y0

在研究过点(x0,y0)的直线l与抛物线x2=2py位置关系时，当l不垂直坐标轴时，可设l：y=k(x-x0)+y0，也可设l：x=k(y-y0)+x0．为避免直线方程代入抛物线方程时出现的平方运算，l方程应优选为y=k(x-x0)+y0．

在研究过点A(0,y0)的直线l与圆锥曲线位置关系时，当l不垂直坐标轴时，可设l：y-y0=k(x-0)，即l：y=kx+y0，也可设l：x-0=k(y-y0)，即x=ky-ky0．显然y=kx+y0优于x=ky-ky0(y=kx+y0中仅一个含字母k的项，x=ky-ky0中有二个含k的项)．

4.优选直线x=k(y-y0)+x0

在研究过点(x0,y0)的直线l与抛物线y2=2px位置关系时，l方程应优选为x=k(y-y0)+x0．在研究过点(x0,0)的直线l与圆锥曲线位置关系时，l方程应优选为x=ky+x0．

例3已知点A(-4,0)，直线l：x=-1与x轴交于点B，动点M到A，B两点的距离之比为2．

(1)求点M的轨迹C的方程；

(2)设C与x轴交于E、F两点，P是直线l上一点，且点P不在C上，直线PE、PF分别与C交于另一点S、T，证明：A、S、T三点共线．

(2016年福建省高中毕业班质检文科数学第(20)题)

对(1)易求C的方程为x2+y2=4,(2)解答如下．

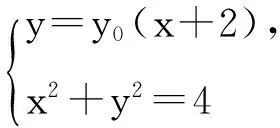
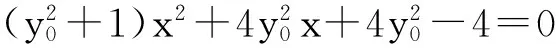
解法2:(优选直线)设E(-2,0)，F(2,0)，P(-1,y0)，S(x1,y1)，T(x2,y2)．设直线PE方程为y=y0(x+2)时，方程中有二个含字母y0的项．

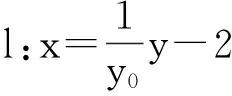
可见在研究直线与圆锥曲线位置关系时，为减少运算量和解题长度，在选择直线方程时，应尽可能减少方程的字母和项数．在直线方程的字母和项数相近情况下，如果圆锥曲线方程中含x的项比含y的项简单，则应选择直线方程为x=ky+b或x=k(y-y0)+x0的形式．否则，选择直线方程为y=kx+b或y=k(x-x0)+y0的形式．