分离产生美
——例谈分离技巧中的数学美
2016-11-09安徽省芜湖市沈巷中学241012
安徽省芜湖市沈巷中学 (241012)
何业亮
分离产生美
——例谈分离技巧中的数学美
安徽省芜湖市沈巷中学(241012)
何业亮
无论是诗人杜牧笔下的“蜡烛有心还惜别,替人垂泪到天明”,还是宋词《雨霖铃》中的“多情自古伤离别,更那堪冷落清秋”.无不体现出人们对“分离”的情感认知——悲愤和伤感.但在数学解题中,“分离”有时不仅能使解决问题变得简单,而且能给人以美的享受.
1.分离常数产生和谐美
分离常数,就是把分子分母中都有的未知数的式子变成分子和分母中有且只有一个含未知数的式子与一个常数的和.
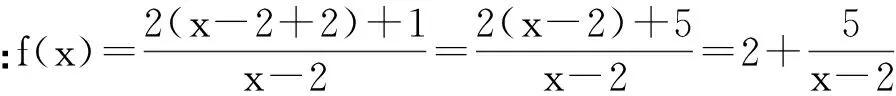
解:∵x>-1,∴x+1>0.∴f(x)=
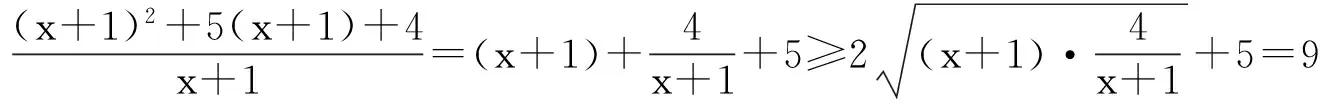

2.分离参数产生简洁美
分离参数,就是在含参数的方程或不等式的变形过程中,将参数分离出来,使方程或不等式的一端化为只含参数的解析式,而另一端化为与参数方程无关的主变元函数.
例3若关于x的二次方程x2+(m-1)x+1=0在区间[0,2]上有解,则实数m的取值范围为.
解法一:(分类讨论)设f(x)=x2+(m-1)x+1,x∈[0,2].
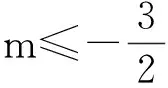
(2)当方程f(x)=0在区间[0,2]上有两解时,
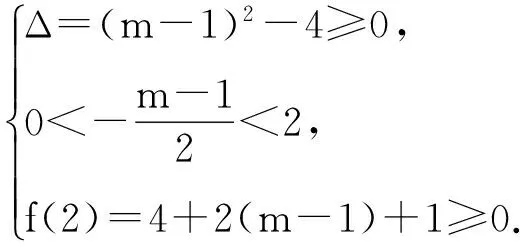
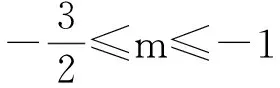
综上所述,实数m的取值范围为(-∞,-1].
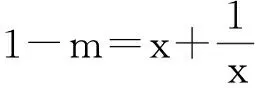
解法一:(分类讨论)f′(x)=

(1)当a≤1时,∵x≥1,∴f′(x)≥0,∴f(x)在[1,+∞)上是增函数.∴f(x)min=f(1)=3+a,∵若对于x∈[1,+∞),f(x)>0恒成立,∴3+a>0,即a>-3,结合a≤1,得-3 综上所述,实数a的取值范围为(-3,+∞) 解法二:(分离参数)∵对于x∈[1,+∞),f(x)>0恒成立,∴对于x∈[1,+∞),x2+2x+a>0,即a>-x2-2x恒成立.∵x≥1,∴(-x2-2x)max=-3,∴a>-3.故实数a的取值范围为(-3,+∞) 赏析:数学家希尔伯特说:“数学中每一步真正的进展都与更有力的工具和更简单的方法的发现密切联系着.”可以说,数学中的简洁美来自于对数学问题深入的分析及恰当的转化.由例3和例4的解答可知,在处理含参数的方程(不等式)有解问题或不等式恒成立问题时,若进行分类讨论,固然能解决问题,但有时显得比较复杂,实践更能证明:对参数进行讨论时,容易出现讨论不全面或运算不准确的错误.若进行分离参数,转化为处理不含参数函数的最值问题,则很容易上手,且计算量较小.细细品味,数学的“简洁美”展现的淋漓尽致,使人由衷地感叹:“分离参数,美哉,妙哉”. 分离函数,就是处理指数函数、对数函数等比较复杂的函数与较为简单的函数的和或商时,将ex或lnx分离出来. (后续工作不再赘述,留给读者完成.不难发现,g′(x)形式非常复杂,即便再次求导,符号也很难判断,问题解决陷入僵局.) 例6设f(x)=(x-1)2ex,判断并证明是否存在区间[a,b](a>1),使函数y=f(x)在[a,b]上的值域也是[a,b]. (若按常规做法,接下来就是构造函数,求导,再构造函数,再求导,过程复杂,计算量大,留给读者完成.下面另辟蹊径——分离函数) 赏析:数学家徐利治教授说过:“奇异是一种美,奇异到极度更是一种美.”从某种程度上讲,数学领域中的一些新的观念、新的方法的产生,就是来自对奇异美的追求.在处理例5和例6时,若按常规解法,面临的是极其繁琐的过程,甚至是无法解答的无奈,势必会导致思维受阻,望“题”兴叹.若巧妙地分离参数,一条“阳光大道”即刻呈现眼前.我们在感慨“山重水复疑无路,柳暗花明又一村”的同时,已然置身奇异的美境之中,为之愉悦,为之赞美,充分感受到数学的奇异美,并为之惊叹,为之陶醉. 亚里士多德曾说过:“虽然数学没有明显地提到善和美,但善和美也不能和数学完全分离.”在多数人认为枯燥的数学解题中,分离小技巧蕴涵丰富的和谐美、简洁美和奇异美.其实,数学美无处不在,正如古希腊数学家普洛克拉斯所言:“哪里有数,哪里就有美.”笔者坚信:数学美不是空谈,而是要去体验、去感受、去欣赏.愿我们都有一双慧眼,能多角度地欣赏到更多的数学美! [1]张奠宙.数学欣赏:一片等待开发的沃土[J].中学数学教学参考(上旬),2014(1/2). [2]文卫星.文卫星数学课赏析[M].上海:华东师范大学出版社,2012. [3]吴成强.例谈一种分离函数技巧的应用[J].中学数学教学参考(上旬),2013(9). [4]新青年数学教师工作室.当代中学数学教育名言解读[M].上海:上海教育出版社,2015. [5]甘志国.证明含“lnx”的不等式的一个小技巧——分离出“lnx”[J].中学数学教学,2015(2). [6]浦静芬.不等式很成立问题的解法探究[J].中学数学月刊,2015(3).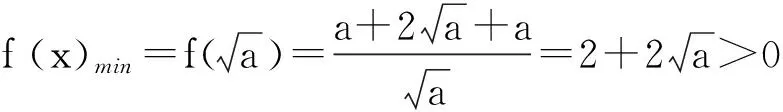
3.分离函数产生奇异美
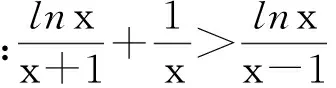

4.结语
