2016年高考江苏卷数学14题的探究与启示

北京市第十二中学　(100071)

刘　刚　赵　毅



2016年高考江苏卷数学14题的探究与启示

北京市第十二中学(100071)

刘刚赵毅

1　试题

(2016年高考江苏，14)在锐角三角形ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是．

试题以人教社B版教材154页第7题“在斜ΔABC中，求证：tanA+tanB+tanC=tanAtanB·tanC．”为依托，考查了三角形中在给定限制条件下代数式最值的问题．试题思维量大，起点高，起到了填空压轴题的作用，有利于区分学生的能力和水平，是一道回归课本的好题．

2　错解及错因

错解:在锐角三角形ABC中，因为tanAtanBtanC=tanA+tanB+tanC，且tanA+tanB+tanC≥

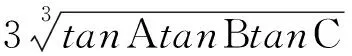
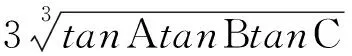
3　解法探究

思路一:利用tanAtanBtanC=tanA+tanB+tanC求解.

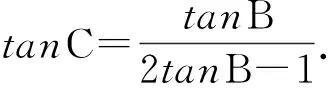
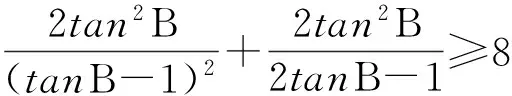
上文已经论述了未经许可演绎作品可依法取得完整著作权，但依然有学者从“应然”的角度认为，未经许可演绎作品取得了著作权后会有损原作品著作权人的利益，即便授予了著作权也应当从权能上予以限制。这都是因为其并未认识到，著作权在行使方式上，在性质上与物权法具有区别。因此，此处将首先探讨著作权与物权所不同的一个特有性质，然后依据该性质来对著作权的行使方式进行分析，最后对部分学者所表现出的担忧予以回应。

点评:解法通过配凑，利用柯西不等式求最值，有一定的技巧性，对于搞竞赛的学生有优势．

点评:导数法是解决最值问题的万能方法，容易操作，是一种不错的选择．上述解法还不严谨，应进一步讨论函数的单调性，但从考试的角度，尤其作为客观题，这样处理显然能节约很多时间．

思路二：消掉角B,C进行求解

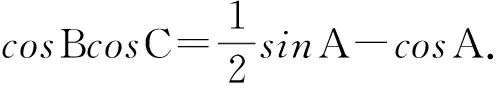
解法3：利用二次函数

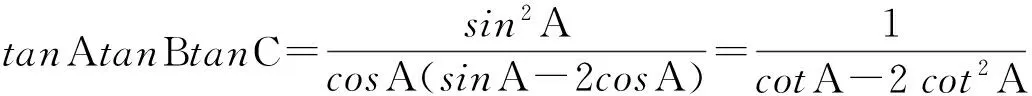
解法4：利用辅助角公式

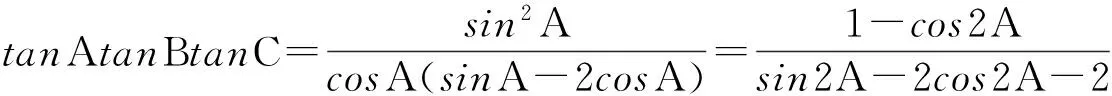
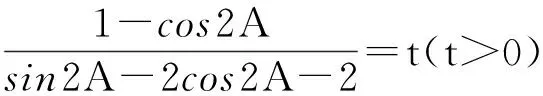
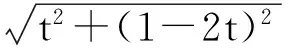
点评:解法通过降幂，使分子、分母变为一次式，通过设参，把分式变为整式形式，然后运用辅助角公式进行解决，这是求最值的一种常用方法．

4　变式

(1)在锐角三角形ABC中，若sinA=2sinBsinC，求tanA+tanB+tanC的最小值；

(2)在锐角三角形ABC中，若sinA=2sinBsinC，求tanA(tanB+tanC)的最小值；

(3)在锐角三角形ABC中，若sinA=λsinBsinC(λ>0)，求tanAtanBtanC的最小值；

(4)在锐角三角形ABC中，若sinA=4cosBcosC，求tanAtanBtanC的最小值；

(5)在锐角三角形ABC中，若sinA=4cosBcosC，求tanAtanB+tanBtanC+tanCtanA的最小值．

解:(1)8；

(2)由sinA=2sinBsinC，得tanB+tanC=2tanBtanC，所以tanA(tanB+tanC)=2tanAtanB·tanC，所以最小值是16；

(3)4λ；

(4)因为sinA=4cosBcosC，所以sin(B+C)=4cosBcosC，即sinBcosC+cosBsinC=4cosBcosC，两边同除以cosBcosC，得tanB+tanC=4．因为tanAtanBtanC=tanA+tanB+tanC=tanA+4=

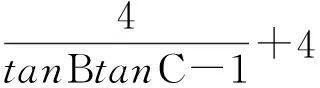
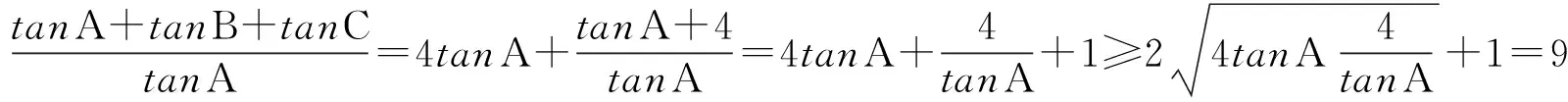
5　启示

教材是集体智慧的结晶，教材中的例习题具有示范性和典型性，是引导与培养学生应用基本理论分析与解决问题的重要参考资料．通过例习题的解决能使学生搞清基本概念，启发学有所用，用有所疑，疑有所思，从而将所学知识融会贯通．所以在复习中，要认真研究每一道例习题，挖掘题目内涵，提倡一题多解、一题多变，形成网络，这样就能少走弯路，复习才会有实效．