与数列有关的不定方程的整数解问题
2016-11-09江苏省丹阳市第五中学212300
江苏省丹阳市第五中学 (212300)
王圣光 李 萍
与数列有关的不定方程的整数解问题
江苏省丹阳市第五中学(212300)
王圣光李萍
所谓不定方程就是未知数个数多于方程个数的方程(或方程组).不定方程解的范围可以是有理数域,整数环,或某一代数数域上的代数整数环.
数列是高中数学的重要内容,又是学习高等数学的基础,在高考中占有极其重要的地位.数列与不定方程知识交汇问题对数学思维能力和探索能力提出了更高的要求,因此在近年来的各省高考试卷(或高考模拟卷)中,这类问题屡见不鲜.
本文拟结合近几年的高考试卷(或高考模拟卷)对与数列有关的不定方程的整数解问题的解法作初步的探讨.
1.利用数论知识
利用数论知识缩小不定方程中未知数的范围是高中阶段求解不定方程的整数解问题的常用方法.
1.1有理、无理分析法
例1(2008·江苏高考19(2))求证:对于给定的正整数n(n≥4),存在一个各项及公差均不为0的等差数列b1,b2,…,bn,其中任意三项(按原来的顺序)都不能组成等比数列.
证明:假设对于某个正整数n,存在一个公差为d的n项等差数列b1,b1+d,…,b1+(n-1)d(b1d≠0).其中三项b1+k1d,b1+k2d,b1+k3d(0≤k1 1.2整数、分数分析法 例2(2009·江苏高考17)设{an}是公差不为零的等差数列,Sn为其前n项和,满足a22+a23=a24+a25,S7=7. (1)求数列{an}的通项公式及前n项和Sn; 解析:(1)an=2n-7,Sn=n2-6n. 例3(2014·江苏高考20)设数列{an}的前n项和为Sn,若对任意的正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”. (1)若数列{an}的前n项和Sn=2n(n∈N*),证明:{an}是“H数列”; (2)设{an}是等差数列,其首项a1=1,公差d<0.若{an}是“H数列”,求d的值; (3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立. 解析:(1)略. (3)略. 1.3正、负分析法 (1)求数列{an}的通项公式; (3)在x轴上是否存在定点A,使得三点Pn(an,2an+5),Pm(am,2am+5),Pk(ak,2ak+5)(其中n,m,k是互不相等的正整数,且n>m>k≥2)到定点A的距离相等?若存在,求出点A及正整数n,m,k;若不存在,请说明理由. (2)存在满足条件的k,k的最小值为5. (3)假设存在定点A,使得三点Pn(an,2an+5),Pm(am,2am+5),Pk(ak,2ak+5)(其中n,m,k是互不相等的正整数,且n>m>k≥2)到定点A的距离相等,不妨设定点A(x0,0).因为n≥2时,an=2n-5,所以Pn(2n-5,22n),Pm(2m-5,22m),Pk(2k-5,22k).因为APn=APm=APk,所以可得 评注:本题判断出不定方程(*)等号左边大于0,右边等于0,从而(*)式不成立,即不存在满足条件的点. 1.4奇、偶分析法 (1)求数列{an}的通项公式; (2)当λ=4时,是否存在互不相同的正整数r,s,t,使得ar,as,at成等比数列?若存在,求出r,s,t满足的条件;若不存在,请说明理由. (3)设Sn为数列{an}的前n项和.若对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,求实数λ的取值范围. 解析:(1)an=(2n+1)λn-1(n∈N*). (2)由(1)知,当λ=4时,an=(2n+1)4n-1(n∈N*).若存在ar,as,at成等比数列,则[(2r+1)4r-1][(2t+1)4t-1]=(2s+1)242s-2,整理得 (2r+1)(2t+1)4r+t-2s=(2s+1)2,由奇偶性知r+t-2s=0.所以(2r+1)(2t+1)=(r+t+1)2,即(r-t)2=0,解得r=t,这与r≠t矛盾,故不存在这样的正整数r,s,t,使得ar,as,at成等比数列. 评注:本题中不定方程(2r+1)(2t+1)4r+t-2s=(2s+1)2等号的右边(2s+1)2为奇数,所以(2r+1)(2t+1)4r+t-2s也为奇数,从而r+t-2s=0,进而得出矛盾. 1.5因式(数)分解分析法 例6(2014·浙江高考19)已知等差数列{an}的公差d>0.设{an}的前n项和为Sn,a1=1,S2·S3=36. (1)求d及Sn; (2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65. 解析:(1)d=2,Sn=n2. (2)由(1)得an=2n-1(n∈N*),所以am+am+1+am+2+…+am+k= 不定方程中未知数的个数多于方程的个数,需要附加另外的条件方程才可解,挖掘题目条件——整数解,所以我们可以利用数论的知识求解不定方程的整数解问题. 当不定方程的实数解集为有界集时,就能用这一必要条件确定整数解的界限,然后逐一检验以确定全部解. (1)求数列{an},{bn}的通项公式; 综上所述,m=1或m=2. 与数列有关的不定方程可以看作以某变量为主元的函数,借助函数的性质,实现不定方程的求解. 例8(2015·江苏高考20)设a1,a2,a3,a4是各项为正数且公差为d(d≠0)的等差数列. (1)证明:2a1,2a2,2a3,2a4依次构成等比数列; (2)是否存在a1,d,使得a1,a2,a3,a4依次构成等比数列?并说明理由; (3)是否存在a1,d及正整数n,k,使得an1,an+k2,an+2k3,an+3k4依次构成等比数列?并说明理由. 解析:(1)(2)略. 评注:本题以不定方程(*)中的未知数m为主元构造出函数f(x),从而将不定方程(*)的解问题转化为函数f(x)的零点问题.利用函数f(x)的性质得出x=1,2,3,4不都是f(x)的零点,即m=1,2,3,4不都是不定方程(*)的解,进而得出结论不存在a1,d及正整数n,k,使得an1,an+k2,an+2k3,an+3k4依次构成等比数列. 高考题在数列与不定方程的交汇处显现的精彩纷呈,解法也是灵活多样的,以上仅列举了几种常见的探求方法,具体情况还应根据题设条件灵活处理.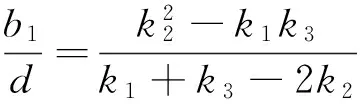
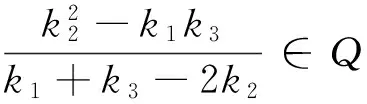
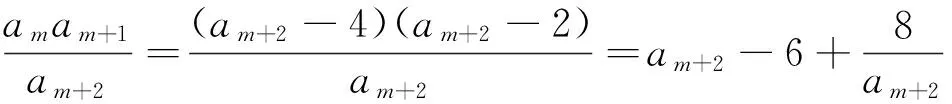
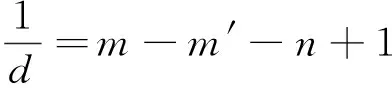
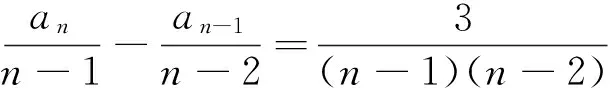
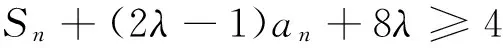
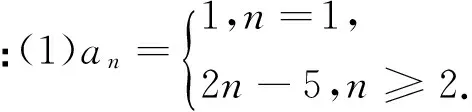
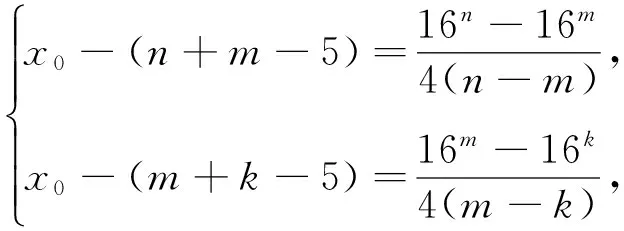
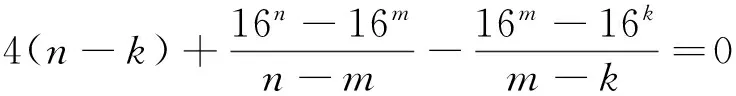
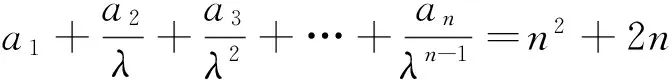
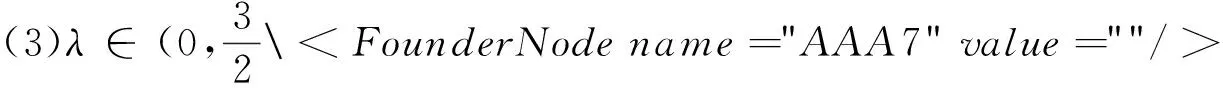
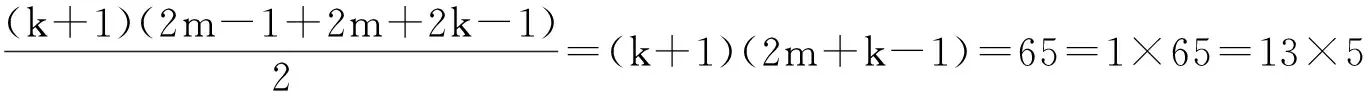
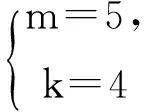
2.利用不等式知识
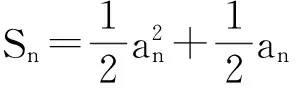
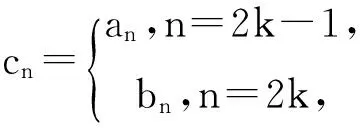
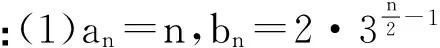
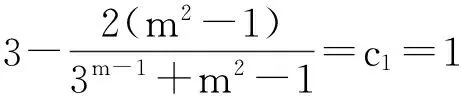
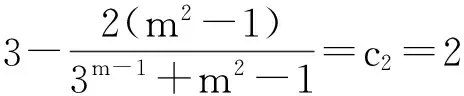
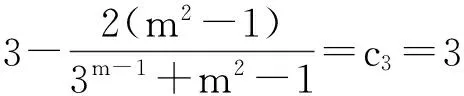
3.利用函数知识