例谈数学解题中的“三等价”

福建省古田县第一中学　(352200)

兰诗全



例谈数学解题中的“三等价”

福建省古田县第一中学(352200)

兰诗全

1　假设的“等价性”

在数学解题中根据解题的需要，合理假设可架起已知与未知的桥梁，达到化繁为简、化难为易的目的．但在运用时一定要注意假设的“等价性”，才能保证解题的准确性、深刻性．

(1)求椭圆C的方程；

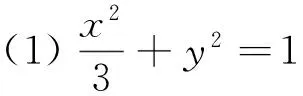
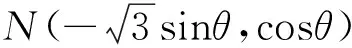
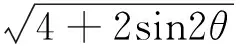
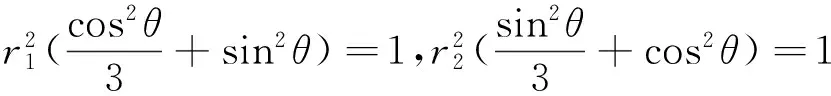
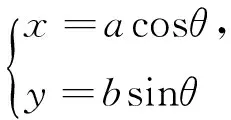
2　解题过程的“等价性”

数学解题过程强调等价性，许多问题需转化，但转化当等价．如何等价地转化，转化是否为等价？这往往决定着解题的成败，值得高度重视．从下例中务必从中“吃一堑、长一智”，补充、完善自己的数学认知结构，努力提高解题完整性、准确性．

例2已知函数f(x)=-x3+ax2+b(x∈R)图像上的任意两点连线的斜率都小于1，求实数a的取值范围．

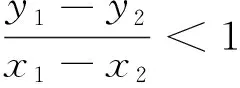
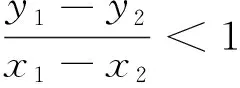
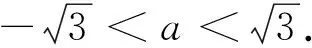
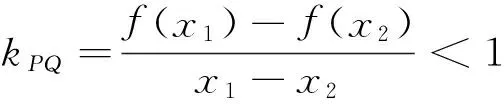
为什么解法1、2与解法3结果不一致呢？我们来细究一番！

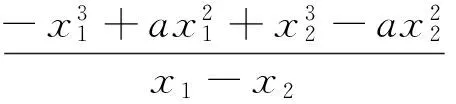
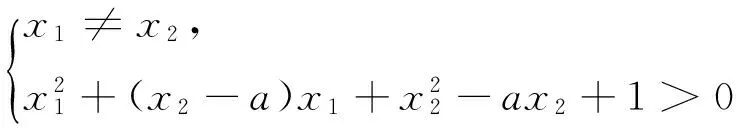
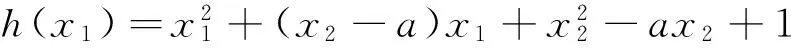
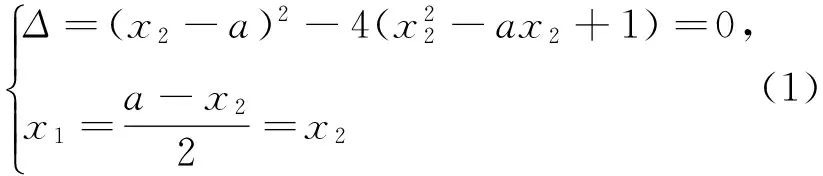
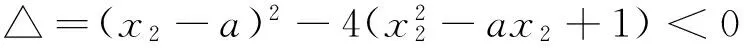
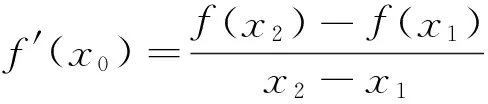
从上可知，满足条件的函数曲线有割线，则必有与割线斜率相等的切线，即{割线斜率}⊆{切线斜率}，但未必有{割线斜率}={切线斜率}．举一反例，根据切线定义，对于函数y=x3图像，在点(0，0)处的切线方程是y=0，但在曲线上找不到割线与切线y=0平行．

解法3突出解题过程的等价性，思路清晰，逻辑严密，为正确解法．

3　结果的“等价性”

为什么求得的结果有的要检验，有的不必检验呢？细究可知，那是因为有的结果只是已知条件的必要条件，有的结果就是已知条件的充要条件．

例3已知关于x的一元二次方程x2+px+q=0两根为p,q．求p,q的值．

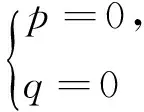
解法2：由已知根据韦达定理得

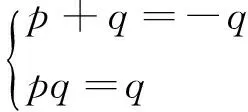
以上解法1、2谁对谁错？循着充分与必要来点击要害．

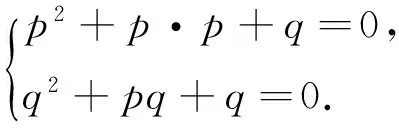
解法2中为什么不要Δ≥0?事实上，对一元二次方程两根为具体存在的数时一定满足Δ≥0．如关于x的一元二次方程x2+px+q=0两根为-1，2，求p,q的值．

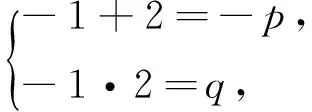
总之，等价转化的思想是解题中最重要的思想之一，要高度重视，细心分析，特别在解方程或不等式中更要注意应用．

*本文系江苏省镇江市教育科学“十二五”规划青年专项课题“在高中数学课堂教学中培养学生思维灵活性的研究”的部分成果，课题主持人：王圣光.