由阿波罗尼斯圆看研读教材的重要性

安徽省合肥市第一中学　(230601)

时英雄



由阿波罗尼斯圆看研读教材的重要性

安徽省合肥市第一中学(230601)

时英雄

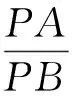
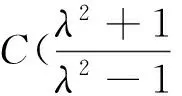
例1(2006高考四川卷)已知两定点A(-2,0),B(1,0),如果动点P满足条件|PA|=2|PB|,则点P的轨迹所包围的图形的面积等于().

(A)π(B)4π(C)8π(D)9π

试题赏析：本题主要考查对阿氏圆的理解，一个比较简单求轨迹问题，求出轨迹是圆，算出半径，进而得到面积.

解：已知两定点A(-2,0),B(1,0)，如果动点P满足|PA|=2|PB|，设P点的坐标为(x,y)，则(x+2)2+y2=4[(x-1)2+y2]，即(x-2)2+y2=4，所以点P的轨迹所包围的图形的面积等于4π，选B.

试题赏析：本题是一道解三角形的问题，一般的思路就是利用余弦定理，再利用面积公式，最后转化成求解最值问题，但如果能利用好阿氏圆的定义，形数结合，就能非常巧妙快速地得出答案.

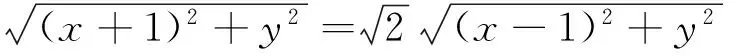
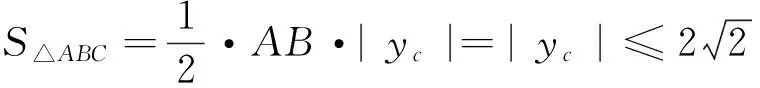
例3(2005高考江苏卷理)如图1,圆O1与圆

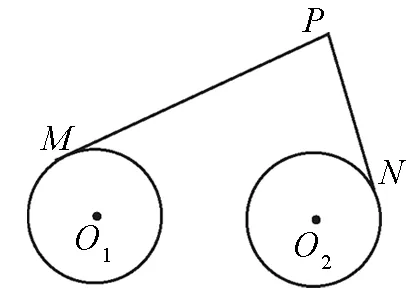
图1

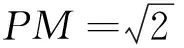
试题赏析：本题其实就是阿氏圆的一个变形，将阿氏圆中的两个定点都膨胀为圆，然后建立平面直角坐标系，利用圆的切线的性质求出动点P的轨迹方程.

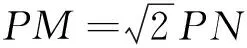
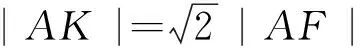
(A)4(B)8(C)16(D)32

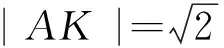
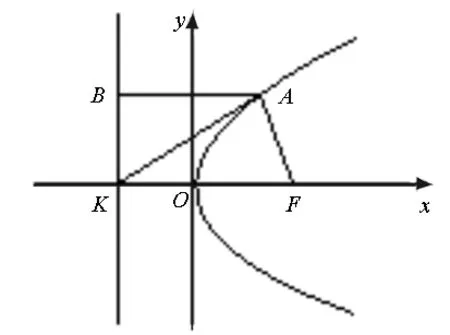
图2

解：如图2，∵抛物线C:y2=8x的焦点为F(2，0)，准线为x=-2，∴K(-2，0).设A(x，y)，由|AK|=

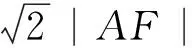
例5(2013高考江苏卷)在平面直角坐标系xOy中，点A(0,3)，直线l:y=2x-4.设圆C的半径为1，圆心在l上.

(1)若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；

(2)若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

试题赏析：注意到第(2)问中MA=2MO，故M点的轨迹是阿氏圆，又M是圆C上的点，所以问题转化为两圆有公共点，即相交或相切，然后由两圆位置关系可顺利解决此题.

解:(1)略.

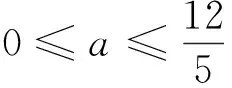
问题溯源

普通高中课程标准实验教科书数学必修2人民教育出版社A版(下称教材)在定义圆的时候就是给出的传统定义，即平面上到一个定点的距离等于定长的动点的轨迹为圆，阿氏圆书本没有直接提出，但是在书中有三处体现，可见其重要性，而且，只要认真研读了教材，就不会陌生，如：

(1)教材第124面习题4.1B组第3题:

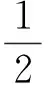
(2)教材第140面信息技术应用,用几何画板探究点的轨迹：圆:

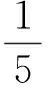
(3)教材第144面复习参考题B组第2题:

已知点M(x,y)与两个定点M1,M2距离的比是一个正数m，求点M的轨迹方程，并说明轨迹是什么图形(考虑m=1和m≠1两种情形).

教学启示

1.立足教材,把握高考.

教材是老师上课之本，学生学习之本，更是高考命题之本，高中数学课本是经过资深专家们深思熟虑、千锤百炼而成，汲取了几十年课程改革的经验.有很多的思考题，探究，习题为学生提供了丰富的具有思想性、实践性、挑战性的反映数学本质的选学材料，拓展了学生数学活动空间，发展学生学好数学、用好数学的意识，重视课本习题潜在功能的挖掘和利用，不仅要弄懂课本提供的知识和方法，还要弄清定理、公式的推导过程和例题的求解过程，揭示例题、习题、复习参考题之间的联系和变换.因为考点在书中，试题在书外，源于课本又高于课本，因此要顺利解答此类题目，必须在掌握课本方法的基础上向外拓展，进行深挖，在教学和复习时不可脱离课本，坚持“以本为纲”，数学教学中，要夯实基础，不要一味的追求解题的难度，以不变应万变.

2.变式探究，提炼思想和方法.

在日常的教学中，需要老师能静下心来，对教材认真研读，深度挖掘，不盲目跟风，课本是试题之源，只要我们能反复研究，在平时的教学中注重变式训练，不仅可以提高学生的数学解题能力，发展不拘一格的意识，而且通过变式来透过现象看清本质，一举切中要害，更重要的是，还可让学生也可从书山题海中解放出来，并使其逻辑思维水平与形象思维水平得到真正的提高，而这也是新课标体系所要求的.课本习题一般都具有典型性、示范性和迁移性，它们或是渗透了某些数学方法，或体现了某些数学思想，或提供了某些重要的结论，因此应充分认识例习题本身蕴含的价值，掌握其中的通性通法.只有平时教学重视思想的渗透，才能让学生在高考选拔中脱颖而出.

3.研习(高中、大学)教材、高考竞赛试题和经典名题，提升教师自身素养.

由试题的背景也可看出，近年来越来越多的命题者在命题时注重了改造经典定理，将数学定理、数学文化、数学史、高等数学知识融入试题中，如最近几年高考题中出现的哥达毕拉斯学派的形数研究、回文数、角谷猜想、斐波那契数列、狄利克雷函数、阿波罗尼斯圆、数书九章中的问题，很多省市高考题用到的高等数学中的伯努利不等式，拉格朗日中值定理，函数拐点，驻点，不动点，凹凸性等背景，“给学生一碗水，自己必须有一桶水”，这些都需要教师在平时的教学中，能够对这些背景有一点了解及给学生灌输这方面的知识，熏陶学生心灵，培养学生对数学学习的兴趣，激发学生对数学学习的热情.也丰富了我们日常教学的内涵.