基于概念本质催生类比思维的本原课堂探究
——以公开课《从圆到椭圆》为例
2016-11-09江苏省南通市天星湖中学226010
江苏省南通市天星湖中学 (226010)
葛建华
基于概念本质催生类比思维的本原课堂探究
——以公开课《从圆到椭圆》为例
江苏省南通市天星湖中学(226010)
葛建华
在对圆和椭圆的系统学习后,我们发现这两种图形存在着许多惊人的相似性,究其原因,其实都缘于它们的“圆”味.基于对两者的研究,笔者设计了这样一堂从探寻联系两者概念本质出发,类比研究相关知识与问题的公开课,体会几何图形的性质都源于其本质,借以提高学生对数学美的鉴赏能力和培养学习数学的兴趣.
1.新课引入,缘于“圆”味
上课伊始,笔者借助几何画板,制作了圆与椭圆的变换动画,让学生感受两者间的某些联系,并进行思考.
师:在我们学习了圆和椭圆,同学们发现它们之间有些相似的地方,那到底有哪些相似之处?
生1:感觉它们都是“圆”的,其他好像只可意会不可言传.
师:很好!它们都有“圆”味.其实这缘于它们的本质属性,我们可以先从两个图形概念本质来研究,看看它们的概念本质上有何相似之处?
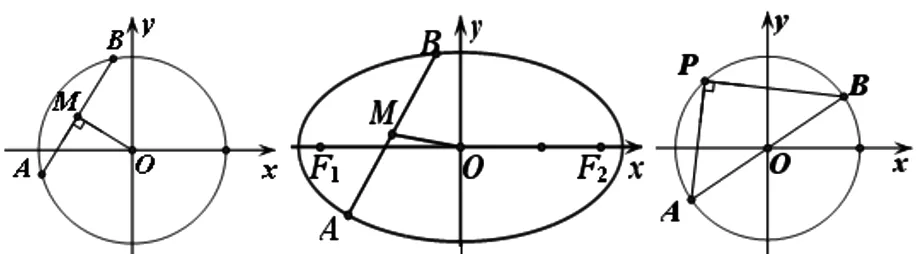
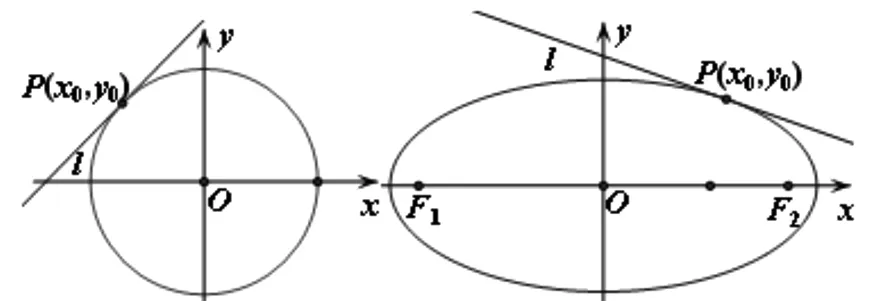
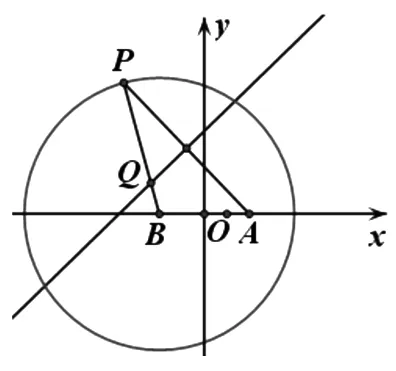
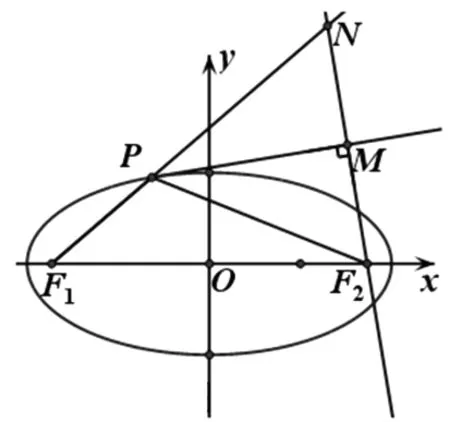
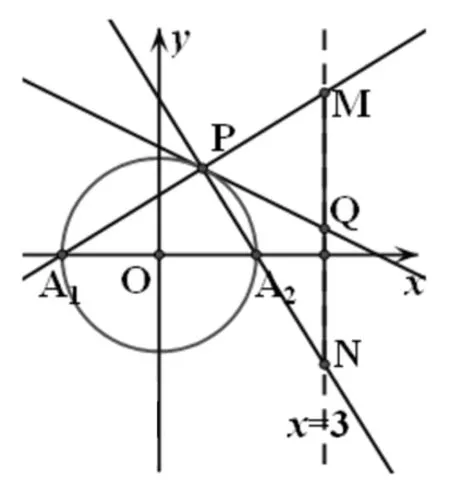
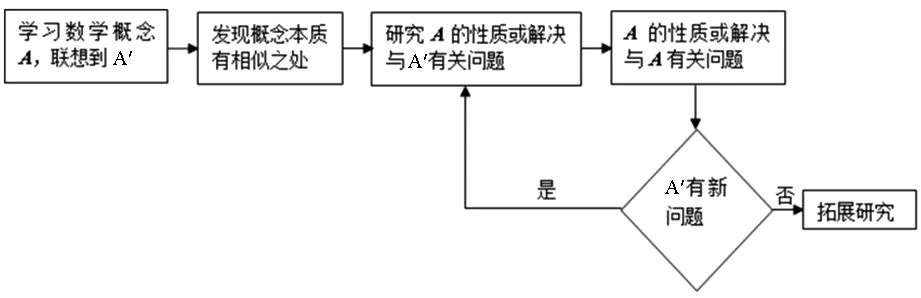
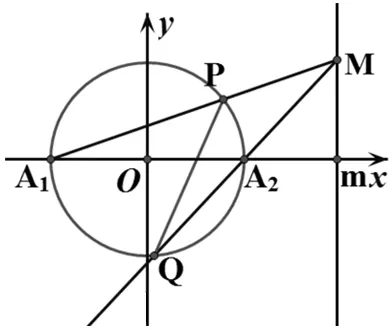
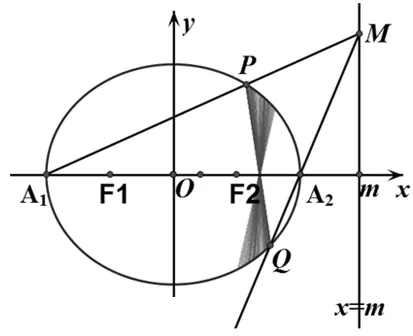
生2:从两个图形的定义看都有两个不同的表现形式.定义1:圆是平面内到定点的距离等于定长的点的轨迹;而椭圆是平面内到两定点F1,F2的距离之和为定长(大于F1F2)的点的轨迹.定义2:圆是平面内到两定点的距离之比为定值λ(λ>0且λ≠1)的点的轨迹(阿波罗尼斯圆);而椭圆是平面内到一定点的距离与到定直线的距离之比为常数e(0 2.1本质联想其他类比 师:还可以从哪些方面来研究它们的联系和统一性呢? 生3:从它们的产生、两图形的变换、方程等角度研究. 引导学生思考,很快发现了圆与椭圆的一些内在的相似性: 2.2结论类比:由圆类比出椭圆中性质 师:既然它们有如此众多的联系,那我们就可以借助类比推理来尝试,看能否将圆中的一些结论推广到椭圆中?从圆中我们比较熟悉的性质开始来研究椭圆,那么圆中有哪些方面的性质? 生4:圆的弦和切线有很多性质. 师:在圆中与弦有关的结论有哪些?(中点弦、相交弦) 生5:(圆中结论1)AB是圆O的弦,点M为弦AB的中点,且AB和OM都不垂直于坐标轴时,则有kAB·kOM=-1.(如图1) 图1 图2 图3 师:如果将弦AB移动,我们会想到移到何处呢?那又有什么样的结论?应怎样得到? 此结论,学生类比运用结论1的做法很快得到了证明. 图4 图5 图6 师:将弦AB所在直线l可以再平移到何特殊位置? 生7:可以平移到使得A、B、M三点重合,那么我们就得到了椭圆的切线,这时椭圆切线有何性质?当然仍然先回到圆中来研究.(圆中结论3)如图5,直线l与圆O相切于点P,且OP与l都不垂直于坐标轴时,则kOP·kl=-1. 师:既然切线有这样的性质,那么我们还会有何发现或想法? 学生的思维似乎活跃起来,都有自己的猜想 生8:椭圆的切线方程与圆的切线方程有相似的地方.(圆中结论4)如图7,点P(x0,y0)为圆x2+y2=r2上一点,则过点P(x0,y0)的圆的切线方程为x0x+y0y=r2. 师:那么,能否类比圆得到椭圆上一点处的切线方程呢?说说怎么得到的?怎样给出严谨的证明?能推广到一般情形吗? 图7 图8 但对于证明似乎学生就无法顺利得到了,于是老师进行了追问:圆中可以通过哪些方法研究得到切线方程,椭圆是否可以借鉴呢? 生10:直接求斜率,不过要分类讨论,利用d=r得到;也可以联立方程组,利用Δ=0来求. 师:很好,注意到了分类讨论,但在椭圆中无法利用这种垂直关系,所以只能从代数角度研究,即分类讨论,联立方程组,消元利用Δ=0来求. 此处我们发现两者在研究方法上具有相似性,都可以借助代数角度来解决,即利用Δ=0来解决,但圆中能借助垂直条件来解决的,在椭圆中则不行,很多时候只能利用方程来解决. 点评:类比是科学研究中常用的一种思维方法,运用此法我们得到了椭圆与圆有如此之多的相似性质.当然椭圆也有其独特性,并非所有的圆的结论都可以类比到椭圆,如相交弦定理,当椭圆中相交弦的倾斜角互补时,相交弦定理在椭圆中才成立.因此在类比时也要注意科学合理,结论的正确与否一定要严谨检验或逻辑证明. 2.3方法类比:由解决圆问题的方法类比研究椭圆问题 根据圆与椭圆的共性,笔者例举两道关联问题(定义法求轨迹). 图9 问题1如图9,P为圆B:(x+2)2+y2=36上一动点,点A坐标为(2,0),线段AP的垂直平分线交直线BP于点Q,求点Q的轨迹方程. 图10 解析:设F2M交F1P延长线于点N,连结OM,则F2N是∠F1PF2外角平分线的垂线,所以PF2=PN,而PF1+PF2=2a,因此PF1+PN=F1N=2a,又OM是三角形F1F2N的中位线,所以OM=a,故可知点M的轨迹是以O为圆心,a为半径的圆,其方程为x2+y2=a2. 点评:注意比较与问题1的联系,其实问题2是问题1的逆向问题,让学生体会到圆与椭圆可能还有其他很多方面的联系,也增强学生继续探索下去的兴趣.两个问题告诉我们遇到轨迹问题首先考虑用定义看轨迹是否为所学图形,否则再考虑用轨迹法,设点解决. 图11 对椭圆问题的解决我们有时会显得力不从心,如果换个角度,先研究解决圆的类似问题,从中探究出解题的出路,再迁移到椭圆上,尝试用解决圆问题的方法来解决椭圆的问题那又会如何呢?因此笔者编了两道拓展研究题让学生亲身体验“圆”的世界,享受缘于“圆”味的快乐. 拓展研究如图11,圆O:x2+y2=1与x轴交于A1、A2两点,P是圆O上异于A1、A2的任意一点,直线PA1交直线l:x=3于点M,直线PA2交直线l于点N,求证:以MN为直径的圆C总过定点,并求出定点坐标. 引导学生分析此题为定点问题,问题的本质就是要求出以MN为直径的圆C的方程,设动直线求交点M、N,还是设动点再表示出直线是两种不同的思路,然后让学生分别用两种不同的思路解题. 拓展探究类比椭圆中也有类似的结论吗?试编出这样一道关于椭圆的一般性问题! 学生类比圆不难得到类似的结论: 图12(1) 图12(2) 图12(3) 点评:从上述研究问题的过程中,发现解决了圆的问题,椭圆的问题似乎就没有什么难度了,再难的椭圆的问题若能运用类似的方法将会柳暗花明. 通过本课的学习让学生总结我们研究问题的一般思维模式: 图13 由于学生的探索热情,还有很多想法,鉴于上课时间关系,所以下面的拓展研究将作为学生课后的微课题研究. 图14 微研究如图14,圆O:x2+y2=r2和直线l:x=m(其中r和m均为常数,且0 图15 微研究类比椭圆中类似可以得到如下问题. 6.1挖掘概念本质利于进行类比思维探索问题 类比思维是将陌生问题转化为熟悉问题的一种创造性思维.要能形成数学中类比两数学知识必须在某些方面尤其数学概念本质上有相同或相似之处,我们才能推出它们在其他方面的相似之处.对数学概念本质的挖掘,我们要能掌握其核心内容,在一定范围内不变的性质,同时也要理解数学概念的不同表现形式及各形式之间的联系,从而深层把握数学概念本质.两个数学概念本质的挖掘能够看清两个数学知识的内在联系,使得类比出的结论更加合理,更切合实际,为研究问题缩短了探索的距离. 6.2类比思维能增强课堂教学的延续性 基于数学概念本质的理解,类比思维中的联想就更有根基.类比思维的运用能够让学生达到举一反三,同时也能激发学生学习数学的兴趣.学生在课堂上对知识的理解与联想将是无穷无尽,然后在教师的适当引导下,课堂教学就变得更具活力,也改变了传统的教学方式,提高了教学的效率.课堂的教学将不再只是讲授知识而是教会学生如何去学习知识,学生感受到知识是自己研究获得的,使得教学能够延续到课后,这种思维能促进学生的终身学习,也增强了学习的延续性. 6.3数学直觉必须科学严谨 类比思维中的联想其实也是一种数学直觉,数学直觉能让我们感知到数学的结论或解决问题的方法,给问题的发现和研究带来一定的帮助,但毕竟只是一种感觉,所以在数学中还需要科学严谨的逻辑验证,如果结论不正确,需要调整分析,重新审视问题直到得出正确的结论.虽然我们不是数学家,但我们应该要用数学家的眼光看问题,需要数学直觉,同时又要有数学家严谨的态度,教学中不断提高学生考虑问题的科学性和严密性. [1]涂荣豹.数学概念本质的把握[J].数学通报,2001(11):18-20. [2]崔宝法.椭圆切线的几个经典性质[J].数学通讯,2006(15):29-30. [3]蔡欣.从类比推理的视角认识椭圆的几个性质[J].中学数学月刊,2014(2):47-48. [4]王新宏.圆的性质在椭圆中的推广及应用[J].中学生数学,2013(11):7-9.2.师生探究,多角度类比
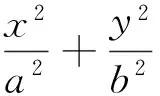
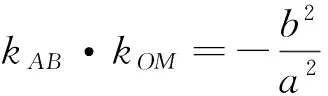
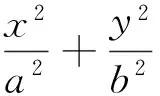
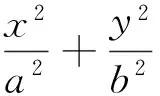
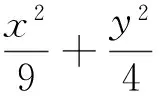
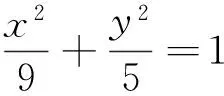
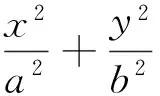
3 拓展研究,多角度解题
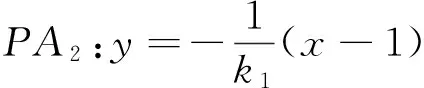
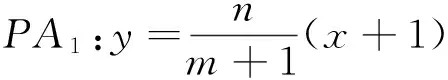
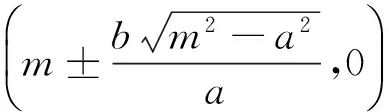
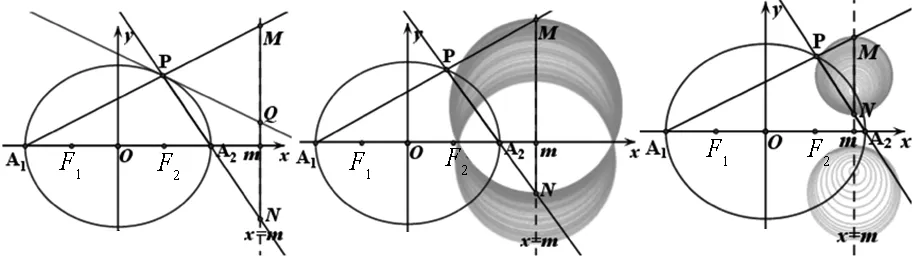
4 反思提升
6 教法感悟
