引入基差影响因素的套期保值模型优化与效用对比分析——以中国大豆加工与经营企业为例

裴勇　刘晓雪

(1. 中国人民大学商学院，100872北京；2. 北京工商大学经济学院，100048北京)



引入基差影响因素的套期保值模型优化与效用对比分析
——以中国大豆加工与经营企业为例

裴勇1刘晓雪2

(1. 中国人民大学商学院，100872北京；2. 北京工商大学经济学院，100048北京)

中国是全球最大的大豆进口国，国内大豆压榨企业在用境外定价中心的期货合约进行套期保值时，面临较大的基差风险。现有套期保值模型中，多将基差作为套期保值模型的不可观测变量，这与大豆压榨企业现实需求不符。为此，将基差影响因素中可解释部分引进套期保值模型，得到基差调整后的套期保值比率和套期保值有效性。运用Copula-GARCH模型实证分析后发现，引入基差影响因素的套期保值模型效果大多数优于原有套期保值模型，这对我国压榨企业的套期保值实践具有重要的指导意义。

基差风险；套期保值比率；Copula-GARCH模型；基差

一、研究背景与研究意义

中国作为全球最大的大豆进口国和需求国之一，我国大豆压榨企业多采取将国外大豆进口至国内压榨成豆油和豆粕后再进行销售的经营模式。 其中，进口大豆原料成本在国际市场上确定，国际市场大豆的现货定价规则是按照芝加哥期货交易所(CBOT)的大豆期货价格加上升贴水来确定的；大豆加工的产品豆粕和豆油则在国内销售。由于国际期货价格和国内产品价格的走势不一致，尤其是当中国买家完成采购，实现从产地向销售地的库存转移，常常出现国外价格上涨而国内市场滞涨的情形，理论界经常使用“定价力缺失”来描述这样的情况。从现实来看，CBOT期货价格和港口现货价格数据表明(见图A)，CBOT期货价格与港口大豆现货价格走势基本一致，其相关性达到0.87，但两者波动都比较剧烈；有时也会出现两者背离情形，如2014年1月至2月曾出现CBOT价格上涨而国内现货价格下滑情形，这种背离给我国大豆加工企业带来极大价格风险。在期货价格和现货价格不出现背离的情况下，进口加工企业套期保值时面临着基差风险，尽管基差波动小于现货价格波动，但波动幅度也比较大，均值为624元/吨，基差均值占现货价格均值(4 054元/吨)的15.39%。这些都表明，基差波动对海外套期保值的企业带来了较大的不确定性，严重时影响着大豆进口加工企业的经营绩效。

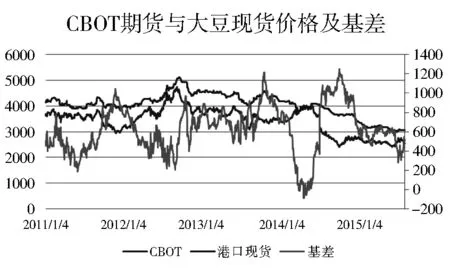
图A　国际市场期货和中国大豆现货价格及基差

注：CBOT为芝加哥交易所近月大豆期货价格，港口现货为中国国内港口进口大豆分销价格，基差为中国现货价格与期货价格之间的价差。

为什么中国是世界大豆最大的买家，而在国际市场的定价势力却与其最大买家的地位难以相称？在套期保值理论中，把期货和现货的差称为基差，基差风险是任何参与期货定价、套期保值都无法回避的风险。在一国之内，现货和期货的基差风险可以通过实物交割进行规避，因此对于美国的大豆贸易商和加工商，由于大豆交割体系在美国国内，他们所面临的基差风险较小。但是对于中国买家，现货市场在中国，期货市场在美国，一旦完成物流运输，进行逆向的期货交割基本没有可能，因此对于中国大豆进口商而言，他们所面临的基差风险远大于美国同行。套期保值的理论研究起源于美国，由于美国国内的现货商面临的基差风险形式和内涵较为简单，所以现代最优套期保值的研究，并没有考虑美国之外的海外套保者如何参与美国期货市场的套期保值。中国作为世界上最大的大宗商品的买家，几乎所有的原料产品定价都在海外期货市场，而生产和销售在中国国内，中国每年进口约8 000万吨大豆，对外依赖度接近90%，因此对中国大豆买家参与CBOT期货套期保值的基差风险研究，是非常重要也是具有现实意义的题目。在基差风险决定因素研究的基础上，才能就定价力、套保策略、最佳套期保值比例等涉及企业套保实践操作的问题，提出分析框架并予以完善。

二、研究方法和文献综述

本文的研究出发点是对国外采购、国内销售的套保者所面临的基差风险进行分析，落脚点是最优套期保值比的改进，即在充分考虑基差风险的前提下，引入了经基差影响因素调整后的套期保值比率模型，以期企业能够最大程度地规避价格风险和基差风险。

本文的研究对象为进口大豆的压榨企业，大豆压榨企业大豆原料成本在境外CBOT期货市场来确定，现货产品销售在国内，主要加工产品分别为豆油和豆粕。因此在CBOT套保的压榨企业面临的基差风险为国内豆油豆粕现货价格和CBOT期货价格之间的差值。但是在实践中，为了规避大豆进口成本和产成品销售价格波动风险，大豆压榨企业往往同时采取在CBOT期货市场买入大豆期货套期保值和大连商品交易所卖出豆油和豆粕期货套期保值，这样的套保方式为联合套保。因此对于压榨工厂的基差分为两部分：一部分是CBOT期货和国内豆油豆粕期货之间的基差，这部分基差主要受到运费、汇率、升贴水、供求关系等因素的影响；第二部分是国内豆油豆粕期货和现货价格之间的基差，这部分基差主要受国内现货供求和交割因素来决定。由于第二部分基差是可以通过交割来进行规避，所以对压榨企业参与CBOT套保面临的基差风险核心是第一部分的基差风险，这也是本文基差因素分解分析的标的。

鉴于此，本文基于中美大豆期货的实际数据，在套期保值比率模型计算中，将第一部分的基差，由不可预测变量转为可观测和不可观测变量两部分，探讨了引入基差风险的套期保值比率和套期保值有效性模型，以期最大程度地规避价格风险和基差波动风险。

关于套期保值比率的计算，经历了“传统套期保值——固定比率套期保值——动态比率套期保值”的发展演变。传统套期保值认为套期保值比率为1，建立与现货头寸数量相同的期货头寸进行套期保值，认为套期保值者参与期货交易的目的是利用期货市场获利弥补现货市场可能的损失，而非通过期货市场获取额外收益。Markowitz(1952)[1]运用投资组合理论来解释套期保值，套期保值比率不再局限为1。Johnson (1960)[2]和Stein(1961)[3]为了规避基差风险，将投资组合理论应用于套期保值研究，并提出以效用最大化为目标的最小方差法(Minimum-Variance，简称MV)模型。即认为套期保值者在期望效用最大化原则下，对现货和期货市场资产进行组合投资。Ederington(1979)[4]在此基础上基于投资组合收益风险最小化、运用最小二乘法(OLS)回归来计算套期保值比率。该方法所得到的回归方程残差往往具有序列相关性，套期保值比率误差可能较大。上述投资组合套期保值方法隐含着现货与期货市场联合分布不变假设，均为静态方法。然而现实中，新信息对市场的冲击以及预期的改变都可能改变现货与期货市场的联合分布，两者之间时变的联合分布便会产生时变的套期保值比率。因此，具有时间依赖性的条件异方差模型(GARCH模型)可较为精确地捕捉现货与期货市场之间联合分布的时变特征，逐步被用来计算动态套期保值比率。Myers(1991)[5]计算并比较了GARCH模型和传统线性模型下的套期保值比率，结果发现，基于GARCH模型条件下的动态套期保值策略效果明显优于传统套期保值法。国内学者大多认为，市场稳定情况下，GARCH模型或者Copula-GARCH的动态套期保值模型策略具有较好效果(朱国华、方毅，2010；张跃军、涂鋆,2010；戴晓凤、梁巨方，2010；王辉、谢幽篁，2011；马超群、王宝兵，2011；邹庆忠、李金林、王贝贝，2011；阎石，2012；史美景、赵永淦，2012；唐韬、谢赤，2015；彭红枫、陈奕，2015)[6-15]，然而，在环境突变期间，根据环境情况可能出现不同情形(付剑茹、张宗成，2014)[16]。此时，简化或静态的套期保值模型，或者将随机冲击、基差滞后期因素考虑进来可能改善套期保值的效果(郑尊信 徐晓光，2009)[17]。

上述研究均通过套期保值将较高的价格风险转化为相对较小的基差风险。此时，基差通常被视为不可预测项，在计算套期保值比率的过程中被视为外生变量。而在实际套期保值中，一方面，在大豆压榨企业国内外多市场的联合套期保值中，基差的波动往往是不容忽视的风险，有时基差波动甚至可能超越价格波动；另一方面，基差并非完全不可预测项，该差值可进一步拆分为运费、汇率、升贴水等确定性成分，对于非确定性成分，也可通过供需状况进行分析。因此，通过期、现货价格分析套期保值比率时，将基差各种可观测影响因素引入套期保值模型中，以期实现在规避价格风险的同时，最大程度地规避基差风险，该做法既贴合企业实践，不是将套期保值停留在理论模型的探讨上，对于指导大豆压榨企业更好进行套期保值交易又具有重要现实意义。

三、引入基差风险的套期保值比率模型的构建

假设期货价格序列为Ft，现货价格序列为St，基差为Bt，则有

Bt=St-Ft

对于不同市场，基差Bt可进一步细分为运费、升贴水等项目，同时也尝试寻找对基差Bt影响较显著的基本面因素，这意味着可以通过运费、升贴水、可获得的基本面数据等，更好地刻画基差，缩小基差中不可捕捉或不可观测的成分。将影响基差的因素分为两类，可解释因素Ct和εt不可解释因素，则有

Bt=εt+Ct=St-Ft

(1)

εt=St-Ft-Ct

(2)

St、Ft、Ct均是可观察部分，通过给予Ft和Ct中可套期保值部分(如海运费、升贴水、汇率等)一定权重，同时结合其他可观察的基本面数据，我们可以得到新的套期保值比例。海运费、升贴水、汇率、基本面因素等对基差波动的贡献率并不相等。我们进一步将可解释因素Ct细分为C0、C1、…、Cn等各种因素，则

Bt=α0C0+α1C1+α2C2+…+αnCn+εt

(3)

其中α0、α1、…、αn分别为C0、C1、…、Cn对基差Bt的影响程度。将基差中的可解释成分与期货价格序列合并，得到新的合成期货价格序列F1t，即

F1t=Ft+α0C0+α1C1+α2C2+…+αnCn

(4)

将合成的期货价格与现货价格序列进行分析，计算相应套期保值比例，假设套期保值比例为h，则意味着最终期货套期保值比例为h；若基差影响因素C0为可套期保值因素(即为升贴水、海运费、汇率等，而非基本面因素)，则C0套期保值比例为α0×h。

在具体的模型形式上，本文选取Copula-GARCH模型。Copula函数主要用来描述随机变量之间的相关性。运用Copula理论，可以将变量的边缘分布和变量间的相关结构分开研究。

在运用Copula函数进行建模分析金融序列时，一般分两步进行：首先，确定单变量金融序列的边缘分布，实际应用中，常采用GARCH族模型计算拟合边际分布，得到标准差和标准残差序列。其次，计算出标准差和标准残差序列后，选取合适的Copula函数来描述各变量之间的相关结构，计算出各变量之间的动态相关系数。在计算期货套期保值比例时，常采用静态和动态的Copula研究，其中基于静态的Copula函数研究方法计算出来的是序列之间的静态相关系数，基于动态的Cpoula函数计算出来的是序列之间的动态相关系数。在选取Copula函数时可根据序列的尾部分布选取正态Copula与tCopula函数，当序列的边际分布是正态函数时选取基于正态Copula函数的分析，当边际分布存在肥尾特征时，选取基于t分布的动态分析。各基于Copula函数的套期保值模型如下。

(一)静态相关正态Copula模型

(5)

其中，δ是随机变量之间的线性相关系数。

(二)静态相关t-Copula模型

(6)

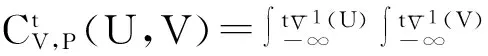
(7)

其中，R12是随机变量之间的静态相关系数。T-copula的密度函数存在对称的尾部相关性，这是它与正态Copula函数的不同之处。

(三)动态相关正态Copula模型

(8)

其中ø-1(·)是标准正态分布的分分位函数，δ是动态相关系数。根据假设，参数δ的变动服从一个类似于ARMA(1，10)的动态过程

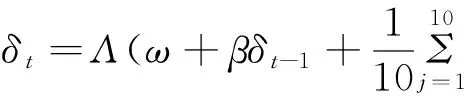
(Vt-j))

(9)

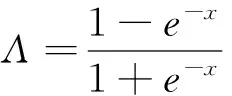
(四)动态相关t-Copula模型

t-Copula相关系数的动态演化方程类似于正态Copula，即

(10)

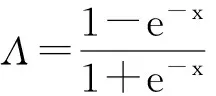
通过上面两步计算出来的序列之间的相关性以及各序列的标准差序列，运用传统的计算套期保值比例方法估算动态套期保值比率。套期保值比率计算公式如下

(11)

其中ρ是变量之间相关系数，Var(ΔSt),Var(ΔFt)是现货和期货序列的方差。

套期保值有效性是通过衡量套期保值后组合的方差相对于未进行套期保值组合的方差降低的百分比。未进行套期保值组合的方差即现货收益的方差，则套期保值有效性的测度公式为

(12)

其中Var(Rst)为现货收益的方差。由公式可知，套期保值有效性越大，Var(Rt)越小，套期保值效果越好。

四、考虑基差影响因素的套期保值模型效果的效用对比分析

(一) 数据选取和处理

国内大豆压榨企业在进口大豆时，通过采购升贴水和运费等、并在芝加哥商品交易所(下称CBOT)点价后完成采购，并在大连商品交易所(下称DCE)按照大豆压榨的出油率和出粕率卖空相应的豆油豆粕实现套期保值。因此本文将选取CBOT大豆价格作为大豆现货价格的估算值，DCE豆油豆粕价格作为期货价格，并将DCE豆油豆粕价格，按照出油率和出粕率折算成大豆价格。国内豆油豆粕期货的活跃合约是DCE的1月、5月、9月合约，导致压榨企业在进行套期保值时只能选择上述3个月份的合约，因此用国内期货合约的连续合约与国外期货合约的连续合约进行分析时，会导致跳跃点较多，不能较好地反映各影响因素对价差的影响。考虑到美豆一般在10月上市，国内企业在采购美豆时一般会选择买入CBOT的11月合约，同时卖出DCE豆油豆粕1月合约进行套期保值。而南美一般是在2月份上市，国内企业一般会选择买入CBOT的3月合约，同时卖出DCE豆油豆粕5月合约进行套期保值。因此本文将分别分析南美作物上市和美国作物上市期间国内压榨企业的套期保值选择，即CBOT大豆11月期货合约对DCE豆油豆粕1月份期货合约、CBOT大豆3月合约对DCE豆油豆粕5月份期货合约。

在对CBOT大豆11月期货合约对DCE豆油豆粕1月份期货合约进行分析时，选取2011年至2014年每年6月份至10月底的期货数据，这是由于6月份开始国外期货市场上的活跃合约逐渐从7月转到11月上，而国内5月期货合约刚刚结束，1月期货合约逐步活跃。这样我们就获得了4段数据(2011、2012、2013、2014)，然后以年份作为截面，各年份序列作为时间序列进行固定效应模型的面板数据回归；CBOT大豆3月合约对DCE豆油豆粕5月份期货合约的样本区间为2012年至2015年每年10月份到次年2月底的期货数据，共四段数据。期货数据均来源于Wind。

汇率分别选取每年11月份、3月的远期汇率报价，数据来源于CME；升贴水采用美湾11月的报价，数据来源于GCD；海运费选取美湾11月的海运费报价，数据来源于贸易商报价；美豆盘面压榨利润为CBOT11月大豆相对于CBOT12月豆油豆粕的压榨利润；猪粮比、港口大豆库存数据来源于JCI，美豆基金净持仓来源于CFTC，国内期货成交持仓比是由豆油和豆粕期货合约的成交量/持仓量，数据来源于Wind。

(二)基差影响因素分析

国内大豆期货价格反映了国内现货的供需状况，因此与国内现货关系较为紧密，但是期货与现货市场还存在一定的基差，主要受持仓成本、远期供需以及期货市场投资者结构等因素影响。本文主要从大豆采购成本、两区域的现货供需状况以及期货市场上的投机因素这三个角度分析两市场基差的波动，其中影响大豆采购成本的选取汇率、升贴水和海运费三个因素，影响国内现货供需的因素选取国内港口的大豆库存和猪粮比两个因素，影响美国市场现货供需的因素选取美豆盘面的压榨利润，影响CBOT期货市场的投机因素选取CBOT美豆基金净持仓，影响国内期货市场的投机因素选取国内期货合约的成交持仓比。

1. 价差影响因素的分析

通过分别对美国新作上市和巴西新作上市时国外期货与国内期货间价差的分析对比，能够更好的体现出影响价差波动的主要因素。在对价差进行建模时，由于影响价差因素较多，需要构建一个多元线性回归模型对其影响因素进行分析。国内大豆与CBOT大豆之间的价差存在一阶自回归，因此在建模时需要加入价差的一阶滞后项，加上价差影响因素，价差影响因素模型构建如下

αt=c+øαt-1+φexchange+φ2fob+φ3freight+αprofit+βratio+λstock+δfund+μvom/int+εt

(12)

bt=c+øbt-1+φ1exchange+φ2fob+φ3freight+αprofit+βratio+λstock+δfund+μvom/int+εt

(13)

其中a,b分别表示美豆3月、11月期货合约与国内大豆期货合约的价差，c是常数项，exchange，fob，freight分别表示汇率，升贴水和海运费，profit表示美豆盘面压榨利润，ratio表示猪粮比，stock表示港口大豆库存，fund表示指数基金持仓净头寸，vom/int表示大连盘期货成交持仓比。φ1，φ2，φ3，ø，α，β，λ，δ表示系数，ε表示随机误差项。

分别对DCE豆油豆粕1月合约与CBOT11月期货价格间价差、DCE豆油豆粕5月合约与CBOT3月期货价格间价差影响因素进行对比分析，结果表明：第一，价差的1阶滞后项在1%的置信水平下对价差影响显著；第二，汇率和升贴水在10%的显著性水平下对价差影响不显著，但在15%的置信水平下显著，且两者的影响系数皆为正，与实际相符，具有一定的参考意义；第三，海运费在1%的置信水平下对价差影响显著，且影响为正，表明海运费确实会增加国内采购企业的成本，从而使得国内期货相对于CBOT期货价格走强；第四，美盘压榨利润在5%的置信水平下对价差影响显著，且影响系数为负，表明美盘压榨利润的高企会对CBOT价格提供支撑；第五，猪粮比在5%的置信水平下对价差影响显著，且系数为正，表明猪粮比的提高对国内大豆需求有益，进而对国内期货价格提供支撑；第六，国内港口大豆库存在5%的置信水平下对价差影响显著，且系数为负，表明库存的增加确实会增加现货的压力，对国内期货价格施压；第七，基金净持仓在1%的置信水平下对价差影响显著，且系数为负，表明基金净持仓的变化确实会对CBOT期货价格带来较大影响，当基金净持仓变大时，CBOT期货价格会走强，反之走弱；第八，连盘成交持仓比在10%的置信水平下对价差影响不显著。

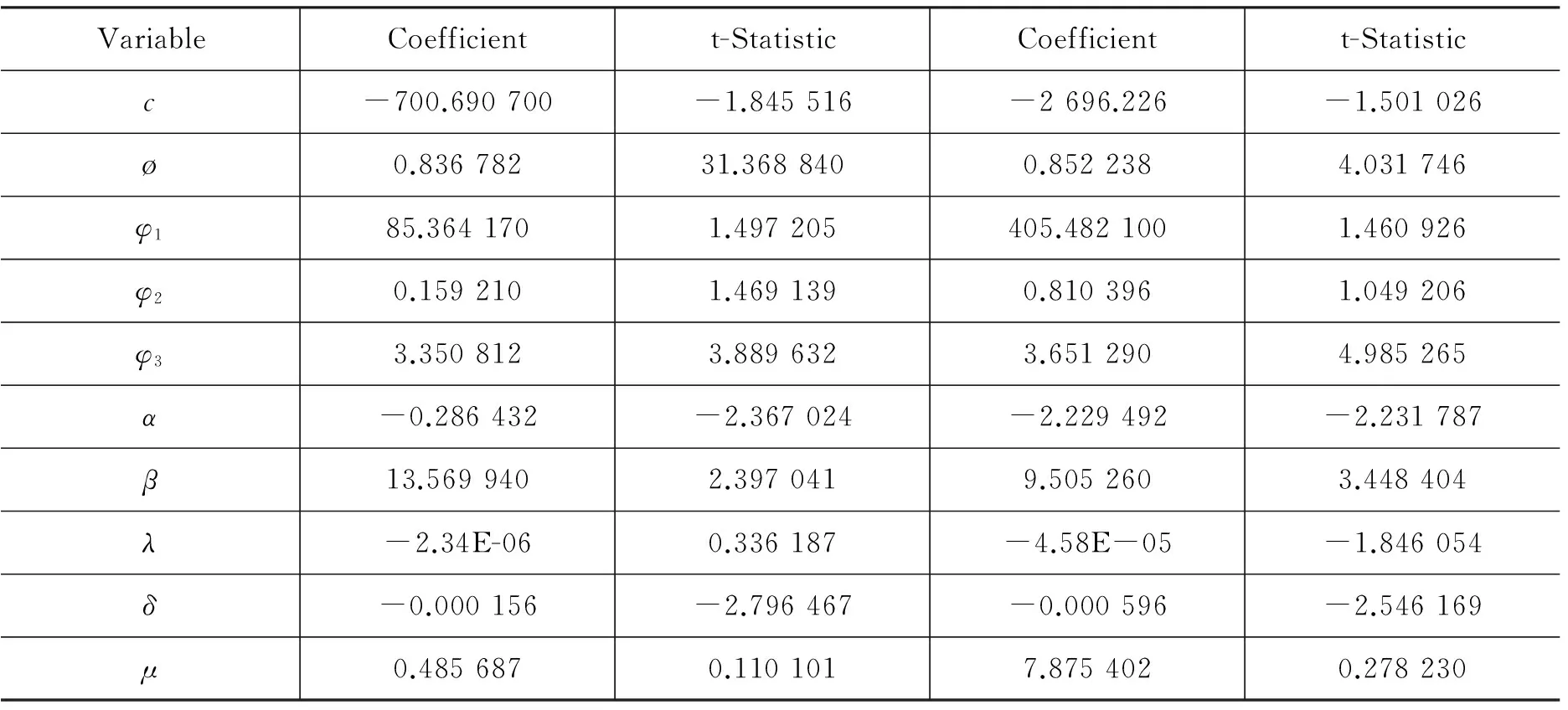
表1　DCE-CBOT价差影响因素分析结果

总体来看，价差一阶滞后项、海运费、美豆盘面压榨利润、猪粮比、港口大豆库存和美豆基金净持仓对DCE和CBOT间价差影响显著，因此在计算套期保值比率时，将这些显著影响因素引入进来考虑。

2. 考虑基差影响因素的套期保值比率的对比分析

考虑到南美大豆和美国大豆的差异性，本文采用面板数据分析方法，分别对CBOT大豆11月期货合约和DCE豆油豆粕1月期货合约、CBOT大豆3月期货合约和DCE豆油豆粕5月期货合约的套期保值比率进行分析，并对比了不考虑基差的影响因素以及考虑基差影响因素下套期保值模型的效果。下文以2011年为例对照了为考虑率基差影响因素和考虑基差影响因素的套期保值比率，其他各年份计算过程和处理方法类似，限于篇幅，仅附上计算结果。

(1)未考虑基差影响因素套期保值比率研究。首先用GARCH模型来拟合国内期货价格和国外期货价格收益率序列的边际分布，其中国内和国外期货序列分别采用GARCH(1，1)模型和GARCH(1，2)模型拟合(见表2和表3)。结果表明：在5%的置信水平下，国内期货价格残差项和波动项均影响显著，在1%的置信水平下国外期货价格残差项和波动项均影响显著。对各模型的残差进行异方差检验，并没有显著的异方差现象，表明模型能够较好的反映序列的波动特征。

表2　国内大豆期货价格收益率波动分析

表3　国外大豆期货价格收益率波动分析

由上述模型得到的期货与现货收益率的条件标准差序列如下图1所示。

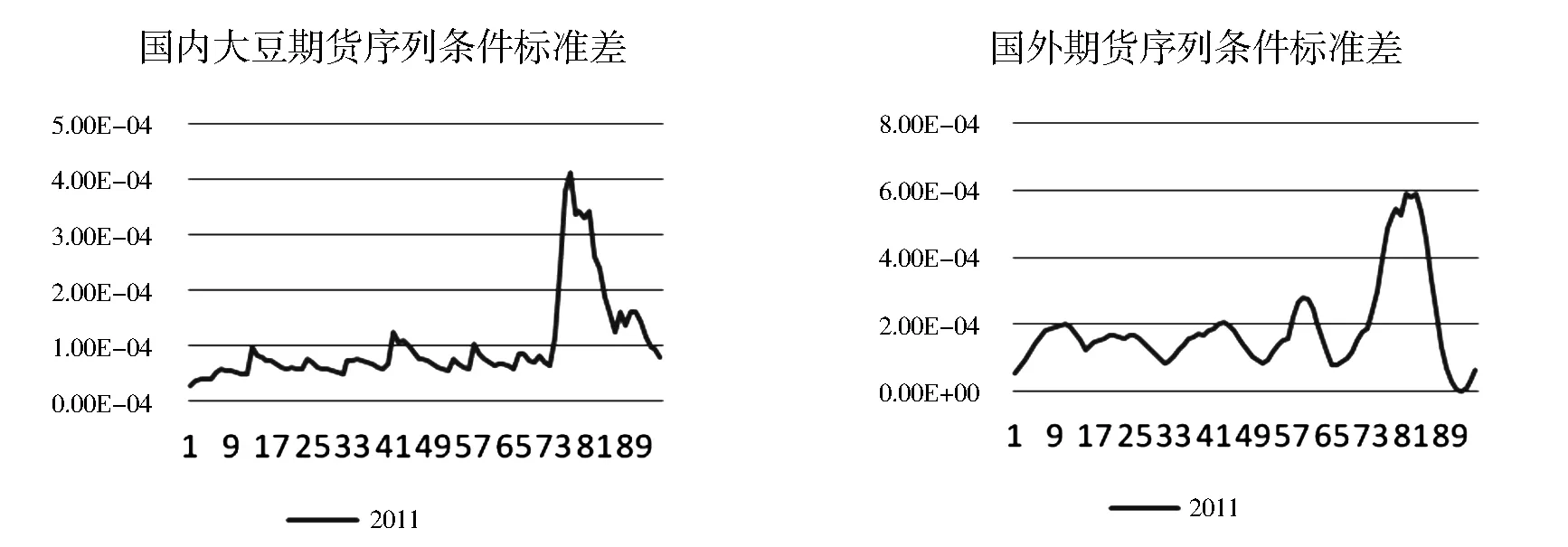
图1　国内期货与国外期货收益率的条件标准差序列

选取二元N-Copula函数描述原始数据的相关结构。通过运行Matlab软件程序，得到两组序列的动态相关系数(见图2)，两组序列相关性主要在0.5-1之间波动，由式(11)计算得到动态套期保值比率(图2)，套期保值比率在0.3到0.9之间波动。

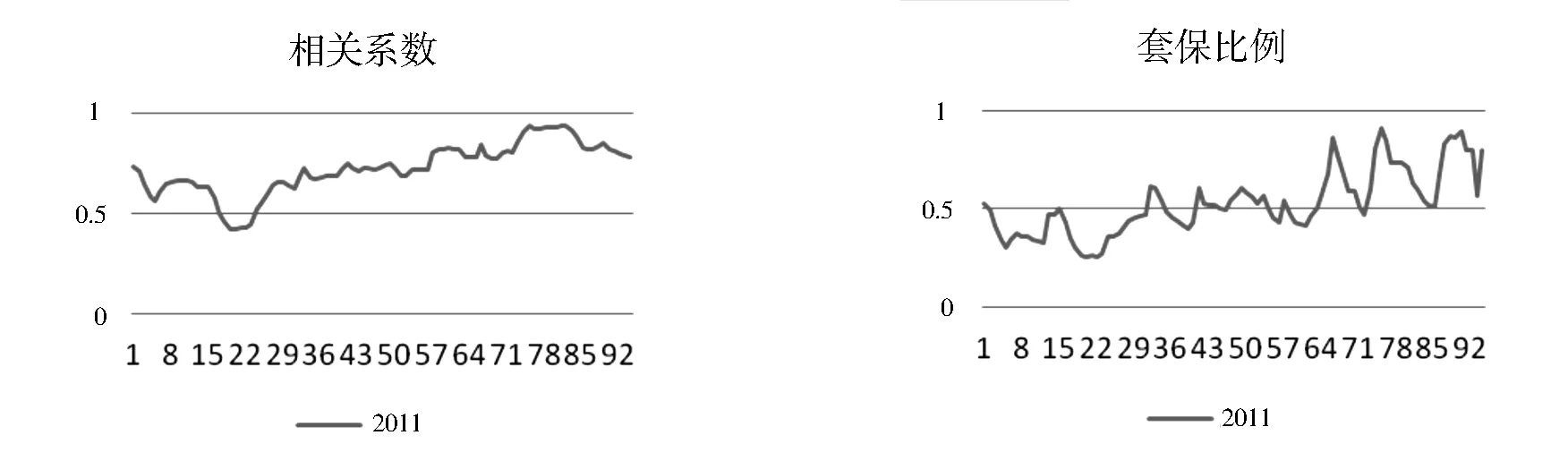
图2　国内期货与国外期货动态相关系数及套期保值比例

运用计算出的动态套期保值比率，通过式(12)计算出考虑基差影响因素的动态套期保值效果，得出该阶段样本区间内套期保值有效性均值为0.551。

(2)考虑基差因素的套期保值比率研究。 运用式(4)对CBOT期货价格序列进行调整，可获得经过价差影响因素调整后的序列。用GARCH(0,2)模型来拟合调整后期货价格序列收益率的边际分布(表3)。结果表明：模型能够较好的拟合，各系数均影响显著，而且对模型的残差进行异方差检验时，并没有显著的异方差现象，表明模型能够较好地反映序列的波动特征。由上述模型得到的调整后的期货序列收益率的条件标准差序列如图3。

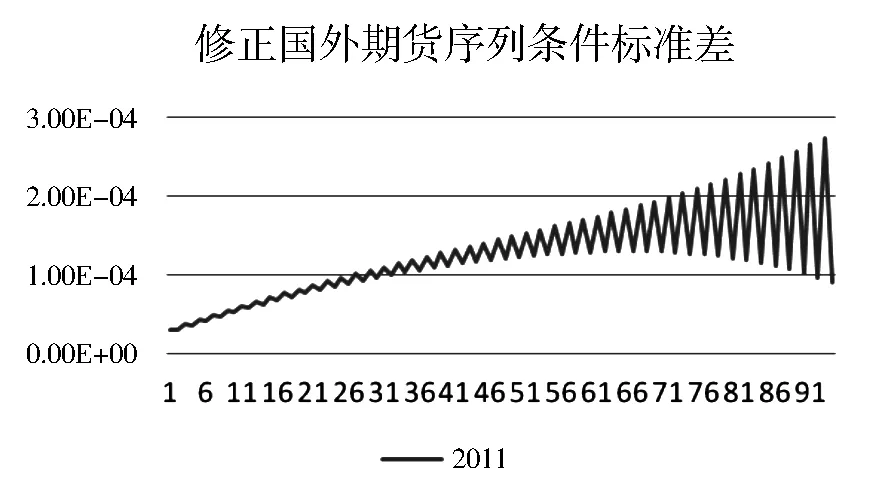
图3　修正国外期货收益率的条件标准差

接下来对现货收益率和修正后的期货收益率序列进行动态套期保值分析，选取二元N-Copula函数描述原始数据的相关结构。通过运行Matlab软件程序，得到了两组序列的动态相关系数(图4左侧)，两组序列相关性基本在0.3～0.8范围内波动。进而测算动态套期保值比率，套期保值比率见图4右侧。套期保值比率在0.3到0.8之间波动，较未通过基差影响因素修正的套期保值比率波动幅度略有降低。

运用计算出的动态套期保值比率，通过式(12)计算出考虑基差影响因素的动态套期保值效果，结果表明：该样本区间内套期保值效果均值为0.811，较未修正的套期保值效果有显著提高。

我们用相同的计算方法对CBOT大豆3月期货合约和DCE豆油豆粕5月期货合约的套期保值比率以及套期保值有效性进行计算，本节实证结果汇总见下表。

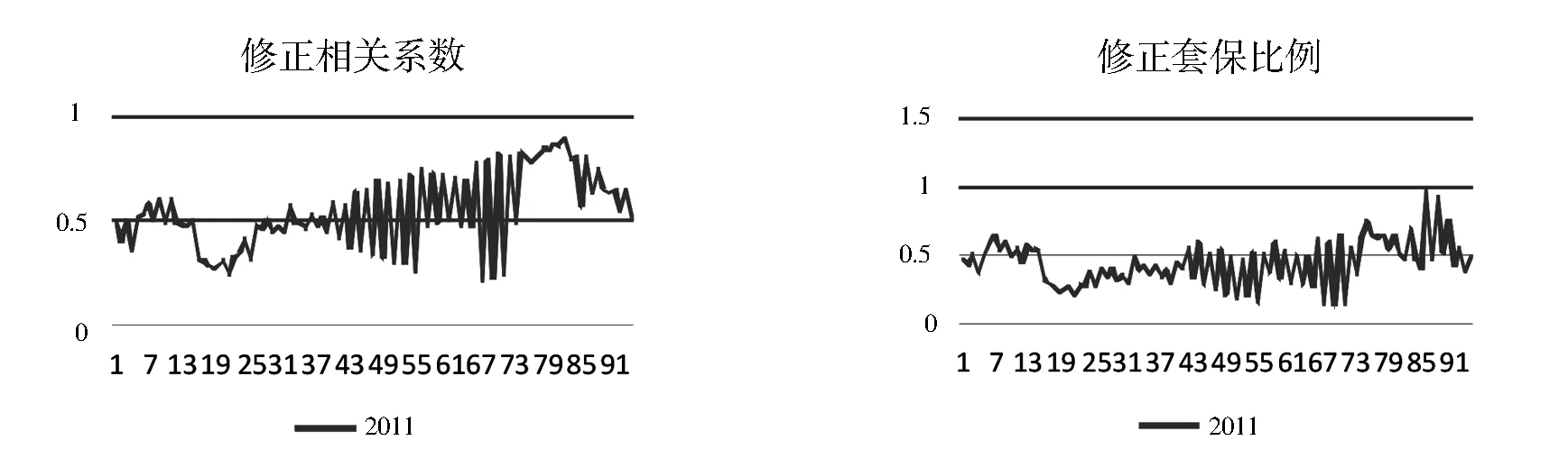
图4　国内期货与修正国外期货动态相关系数及套期保值比例

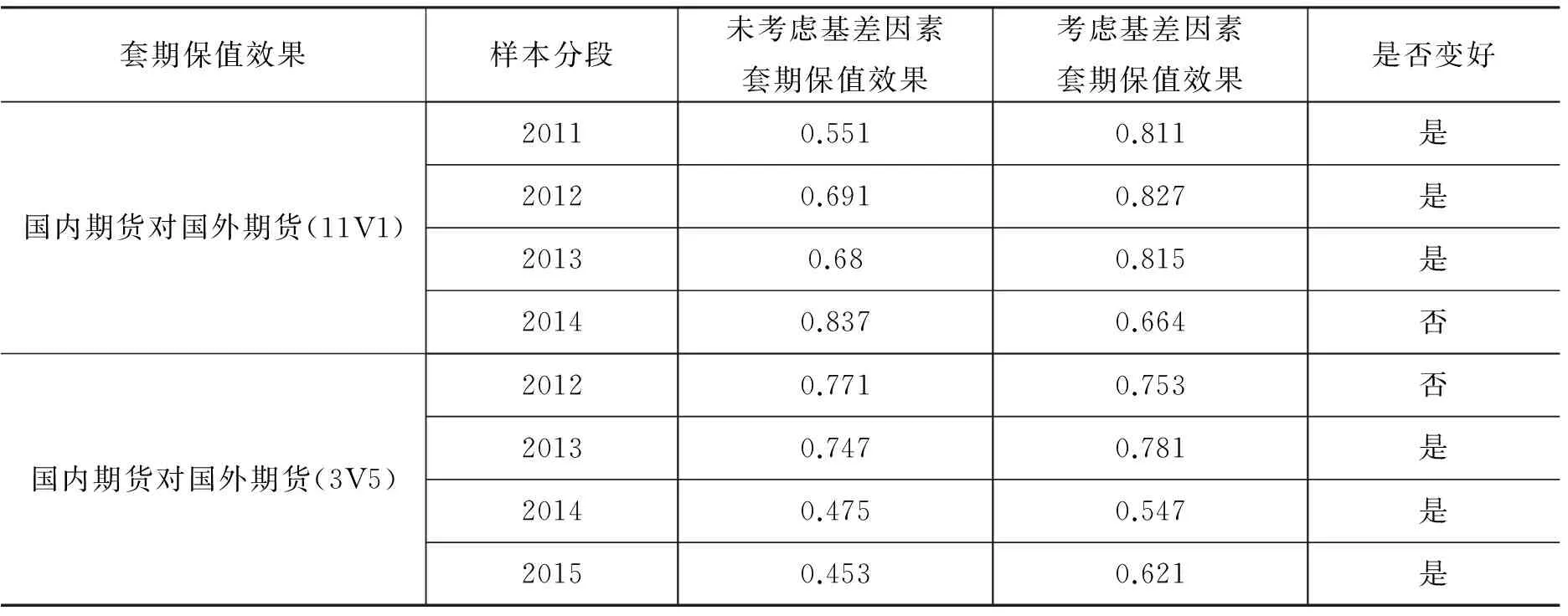
套期保值效果样本分段未考虑基差因素套期保值效果考虑基差因素套期保值效果是否变好国内期货对国外期货(11V1)20110.5510.811是20120.6910.827是20130.680.815是20140.8370.664否国内期货对国外期货(3V5)20120.7710.753否20130.7470.781是20140.4750.547是20150.4530.621是

注：根据本文计算结果整理而成。

上表结果表明，8组国内期货与国外期货之间的价格序列进行套期保值分析后，有6组考虑基差影响因素后的套期保值效果好于未考虑基差影响因素的套期保值效果。

研究结果表明：

第一，总体来看，在套期保值模型中考虑基差影响因素后，企业套期保值效果多数情况下优于不考虑基差影响因素的套期保值模型。

第二，国内期货与国外期货之间的套期保值效果不甚理想，即使考虑基差影响因素后，国内期货和国外期货之间的套期保值组合效果整体上在0.547～0.827之间波动，这是因为，国内期货市场没有能够直接对应美国大豆的标的，因此使用豆油豆粕折算的大豆价格作为国内期货价格，因此，在国外期货与国内期货间基差还包含了压榨利润影响，基差波动相对更为频繁，这在一定程度会影响套期保值效果。

第三，从分月份套期保值来看，11月外盘对国内1月合约的套期保值效果，整体高于3月外盘对国内5月内盘套期保值效果，这可以通过基差进一步解释。CBOT的大豆期货价格，更多代表了美国国内的供需状况，因此与美国供需联系更为紧密。而11月所代表的，是美国新季大豆，因此其基差波动相对较小；3月合约所处时期是南美新豆上市时段，而3月合约价格仍更多的是反映3月时美国国内的大豆供需情况，南美丰收压力也体现在南美当地基差上，这意味着以CBOT大豆期货与大连商品交易所豆油豆粕期货所折算的基差波动将更为剧烈。总而言之，贸易流的改变，进而导致基差波动的改变，是造成11月合约套期保值效率高于3月的原因。

五、主要结论和相关启示

国内大豆压榨企业在进口大豆、销售豆油和豆粕的这种模式下，在海外套期保值时经常面临着基差波动风险，为此，使用国内外期货市场的价格数据，运用Copul-GARCH模型建立了经基差影响因素调整后的套期保值比率模型。即在套期保值比率计算时，不再将基差作为不可解释的变量，而是充分考虑了各因素对基差的影响程度，形成引入基差影响因素的套期保值的模型。将该模型与未经基差影响因素调整的套期保值比率模型运行效果进行比较分析，结果表明：

第一，本文提出的引入基差影响因素的套期保值模型对于大豆压榨企业具有重要的现实意义，套期保值比率和套期保值效果的计算结果表明，经基差影响因素调整的套期保值效果在0.547～0.827之间，未经基差影响因素调整的套期保值效果约在0.453～0.837之间，经基差影响因素调整的套期保值模型的效果多数情况下优于未经基差影响因素调整的套期保值效果，稳定性也高于未经基差影响因素调整的情况。这也意味着，不仅基差的波动会影响套期保值效率，企业在进行套期保值时也需要关注基本面因素对基差的影响，甚至通过一定手段对基差中可套期保值的部分进行套期保值。

第二，基差影响因素的实证分析表明，基差一阶滞后项、海运费、美豆盘面压榨利润、猪粮比、港口大豆库存和美豆基金净持仓对DCE和CBOT之间价差影响显著，能够有效解释价差的部分波动，也成为套期保值比率中价差影响因素的重要可解释变量。

第三，尽管引入基差影响因素的套期保值模型的效果优化了原来的套期保值模型，但是国内期货与国外期货市场之间的套期保值效果仍不够理想，主要因为国内期货市场没有直接对应美国大豆的标的，使用豆油豆粕折算的大豆价格时包含了压榨利润的影响，在一定程度上影响了套期保值效果。

第四，从分月份套期保值来看，11月外盘对国内1月合约的套期保值效果，整体高于3月外盘对国内5月内盘套期保值效果。

第五，在套期保值比率模型的计算中，可得到影响基差的各因素的最优套期保值比率。企业使用得到的最优套期保值比率h在期货上进行套期保值时，也可得到对基差中可套期保值部分的套期保值比例，例如对于可套期保值影响因素(如运费)，动态套期保值比例为×h。

第六，基于基差影响因素来改进最优套保比例，对于企业套保实践的指导意义在于如下两个层面：

一是对于微观层面而言，大豆压榨企业如果使用CBOT期货市场进行套期保值，必须要考虑海运费、美豆盘面压榨利润、猪粮比、港口大豆库存和美豆基金净持仓等因素。企业套期保值，不仅要对冲期货价格的风险，还要对上述因素带来的风险进行对冲管理。上述因素中，海运费、美豆盘面压榨利润均有相应的的期货合约来进行风险管理。对于猪粮比、港口大豆库存和基金持仓的因素，构成企业套保实践中需要密切关注的因素，上诉因素发生变化，企业的套保比例可能就要相应进行调整。

二是中观层面而言，关于提高定价力的启示，要增加中国大豆买家在国际市场的定价力，完善不同层次的基差市场建设对于期货定价和套期保值的意义重大。由于基差对于套期保值效果影响较大，因此，完善基差市场，将整个现货市场定价置于期货市场，会增强期货和现货市场的联系。对于中国现存的商品期货市场(大连、郑州和上海)，应重点推进以本市场期货合约为定价基准的、可标准化基差的市场建设；而各类的远期交易市场或者专业化的交易市场，应重点推进非标准化基差的市场建设，比如上海航运运价交易所目前设计上市交易的非标准化基差合约，就在试图将中国进口商面临的基差中控制的诸多因素，比如运费、汇率等设计为一份可交易的合约，通过参与这个合约的交易，中国进口商就可以控制和对冲基差上述的影响因素影响，从而为控制基差因素、优化最优动态套期保值比例，提供了交易工具，使得理论研究真正能落实在实践中。

[1]Harry M Portfolio Selection. The Journal of Finance, 1952,7(1):77-91

[2]Johnson LL. The Theory of Hedging and Speculation in Commodity Futures[J].Risk Uncertainty &Profit, 1960, 27(2):297-298.

[3]Stein J. The Simultaneous Determination of Spot and Futures Prices[J].American Economic Review,1961,(5):1012-1025.

[4]Ederington L H. The Hedging Performance of The New Futures Markets[J].Journal of Finance, 1979,34(1):157-170.

[5]Myer S R J. Estmating Time-varying Optimal Dynamic Hedging Ratios on Futures Markets[J].Journal of Futures Markets,1991,11:39-53.

[6]朱国华, 方毅. 套期保值的有效性及其评价[J].证券市场导报,2010(11):55-60.

[7]张跃军, 涂鋆.中国燃料油期货市场动态套期保值研究——基于Copula-GARCH模型的实证分析[J].北京理工大学学报,2010(11):55-60.

[8]戴晓凤, 梁巨方. 基于时变Copula 函数的下偏矩最优套期保值效率测度方法研究[J].中国管理科学，2010(12)：26-32.

[9]王辉, 谢幽篁.中国商品期货动态套期保值研究:基于修正ADCC和DADCC-GARCH模型的分析[J].世界经济，2011(12)：120-139.

[10]邹庆忠, 李金林, 王贝贝.基于时变相关copula的最小方差套期保值研究[J].北京理工大学学报，2011(11)：1383-1386.

[11]马超群, 王宝兵. 基于Copula-GARCH模型的外汇期货最优套期保值比率研究[J].统计与决策,2011(12):124-128.

[12]阎石, 邹尔康. 我国大豆期货套期保值比率及策略的有效性检验[J].宏观经济研究，2012(5)：88-104.

[13]史美景, 赵永淦. 基于Copula-TGARCH模型的股指期货最佳套期保值比研究 [J].数理统计与管理，2012(3)：354-362.

[14]唐韬, 谢赤. 基于状态转换动态 Copula 模型的外汇套期保值研究[J].中南大学学报(社会科学版)，2015(2)：104-110.

[15]彭红枫, 陈奕. 中国铜期货市场最优套期保值比率估计——基于马尔科夫区制转移GARCH模型[J].中国管理科学，2015(5)：14-22.

[16]付剑茹, 张宗成.模型的复杂性与期货套期保值效率：基于环境突变样本区间的检验[J].管理工程学报，2014(4)：146-151.

[17]郑尊信, 徐晓光. 基差、随机冲击与不对称相关结构下的期货套期保值——来自亚洲股指期货市场的证据 [J].数量经济技术经济研究，2009(3)：91-104.Empirical Study on Hedging Model Considering the Impact of Basis——Based on the Example of Chinese Soybean Crushers

责任编辑廖筠

PEI Yong1, LIU Xiao-xue2

(1. School of Business, Renmin University of China, Beijing 100872, China; 2. School of Economics, Beijing Technology and Business University, Beijing 100048, China)

China is the largest soybean importer in the whole world, and most of the Chinese soybean crushers are faced with huge basis risk when they hedge in oversea pricing futures market. However, basis is always treated as an unobservable variable in the existing research of hedging models, which cannot satisfy the practical need of soybean crusher. Therefore, it attaches such practical significance to the academic research and soybean transactions that the explicable part of the basis variable is applied to hedging model to obtain the adjusted hedging ratio and hedging effectiveness. Five main conclusions are carried out through the empirical study based on the Copula-GARCH model. Specially, we found the hedging models considering the impact of basis in most cases behave better than the original ones. This conclusion might be helpful for Chinese crusher to reconsider their hedge strategy on oversea futures market.

basis risk; hedging ratio; Copula-GARCH model; basis

2016-02-06

北京市属高等学校创新团队建设与教师职业发展计划项目(IDHT20130505);国家社会科学基金重大项目(14ZDA034)。

裴勇，男，中国人民大学商学院博士生，主要从事期货市场、大宗农产品贸易研究；刘晓雪，女，北京工商大学经济学院副教授，主要从事衍生品市场与农产品市场研究。

F830.9

A

1005-1007(2016)04-0054-11