弹性参数各向异性对页岩井周应力的影响

曹文科，邓金根，蔚宝华，刘 伟，李 扬

(中国石油大学(北京) 油气资源与探测国家重点实验室，北京 102249)



弹性参数各向异性对页岩井周应力的影响

曹文科，邓金根，蔚宝华，刘 伟，李 扬

(中国石油大学(北京) 油气资源与探测国家重点实验室，北京 102249)

为研究层理性页岩地层井周应力分布及其对井壁稳定性的影响，针对页岩力学参数的各向异性特点，建立了基于横观各向同性材料本构关系的弹性理论分析模型，运用该模型计算井周应力，并与各向同性材料下的应力分布进行对比，获取了页岩地层弹性参数各向异性对井周应力分布的影响规律，同时对井壁稳定状况进行了评估。研究表明：井周应力分布对弹性模量各向异性的敏感性强于泊松比各向异性，相同的弹性模量与泊松比各向异性影响下的井周应力分布形态具有相似性，但弹性模量与泊松比各向异性比的增减导致的井周应力增减变化相反，弹性参数各向异性对井壁破裂压力的影响远大于对坍塌压力的影响，显著地影响井眼近井壁地带的破裂压力。

井周；应力分布；横观各向同性页岩；井壁稳定

曹文科，邓金根，蔚宝华，等.弹性参数各向异性对页岩井周应力的影响[J].西安石油大学学报(自然科学版)，2016，31(5):27-35,42.

CAO Wenke,DENG Jin'gen,YU Baohua，et al.Effect of anisotropy of elastic parameters of shale formation on stress distribution around wellbore[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(5):27-35,42.

引　言

随着美国页岩气革命在国际上引发的非常规能源开发热潮，我国的页岩气开发事业正蓬勃兴起[1]，然而四川页岩气的钻井作业表明井壁坍塌与漏失等失稳问题时有发生。页岩井壁失稳问题归根结底是因为在页岩地层钻井之后井周应力状态发生改变，当发生应力集中而重新分布的应力满足岩石的破坏准则时井壁发生破坏。基于页岩的层理性构造，页岩具有各向异性特征，可视为横观各向同性材料。衡帅等[2-3]对页岩的各向异性力学参数进行了测量，崔杰等[4-7]运用解析方法和数值方法对各向异性地层中的井周应力分布进行了求解，卢运虎等[8-13]建立了各向异性地层下的井壁稳定计算模型，然而目前对页岩井眼应力和井壁稳定的分析多针对井壁处，同时井壁稳定计算往往只考虑了强度的各向异性，而对考虑弹性参数各向异性下的井周区域的应力分布尚缺乏研究。本文基于横观各向同性材料本构关系，运用弹性理论对页岩井眼钻开后的应力分布进行研究，通过与各向同性材料下的应力分布进行对比，获取页岩地层弹性参数各向异性对井周应力分布的影响规律。

1　页岩的各向异性

页岩一般为硬脆性泥页岩，图1为重庆龙马溪组页岩，页岩在经历深部地层较高压力和温度的长期作用下，因矿物颗粒的择优取向，黏土矿物形成定向排列，同时黏土矿物多为片状结构，不同层次间矿物发育了不同级次的层间与层内微裂缝，构成微裂缝网络，黏土矿物的定向排列与微裂缝的发育促使页岩具有鲜明的层理性特征(图2)，因而形成了页岩地层的各向异性特征。为便于对页岩力学特性进行分析，运用连续性介质弹性理论，将页岩视为横观各向同性介质(图3)，即页岩层理面方向弹性模量与泊松比为各向同性，均为Eh,νh，层理面法向方向弹性参数为Ev,νv，具体参数的获取可运用室内岩石力学实验法与现场偶极横波测井法[14-15]。

图1　重庆龙马溪组页岩Fig.1　Photo of Longmaxi shale in Chongqing

图2　龙马溪组层理页岩微观结构电镜扫描图Fig.2　SEM scan picture of Longmaxi Formation laminated shale

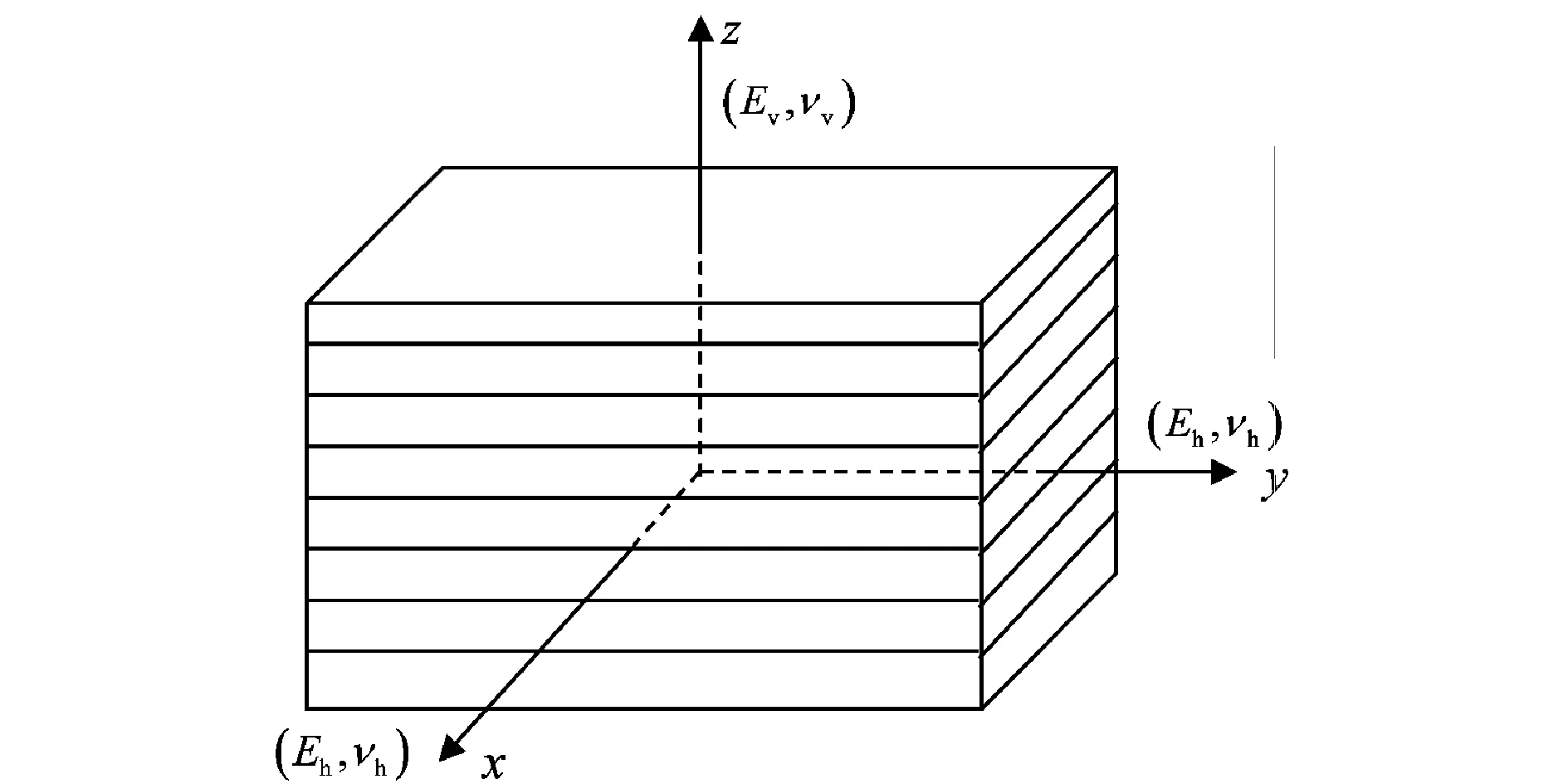
图3　 横观各向同性介质坐标系Fig.3　Coordinate system for transversely isotropic material

2　各向异性地层井周应力分布

根据广义胡克定律，各向异性材料应变-应力关系为：

εij=Cijklσkl。

(1)

式中：εij，σkl分别为应变张量与应力张量，Cijkl为弹性柔度矩阵，横观各向同性材料具有5个独立参数，分别为Eh,Ev,νh,νv,Gv，用独立参数表示的应变-应力关系为

(2)

一般情况下可视上覆岩层压力为垂直向主地应力，地应力坐标系下的3个主地应力分别为σH,σh,σv，按照坐标变换方法可将三主地应力转换到井眼直角坐标系下的应力，即可得到井眼钻开后远场地应力(σx0,σyo,σzo,τxy0,τxz0,τyz0)的表达式，同时将应变-应力系数矩阵Cijkl经一系列坐标变换， 转换至井眼直角坐标系下，根据Lekhnitskii[16]和Aadnoy[13]等推导的解析公式，将远场地应力、井眼钻开形成的地应力与钻井液液柱压力三者叠加，可得横观各向同性页岩井眼直角坐标系下的井周应力分布。

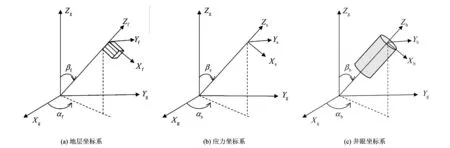
图4　参考坐标系Fig.4　Crustal stress, formation and borehole coordinate systems

(3)

其中：

(4)

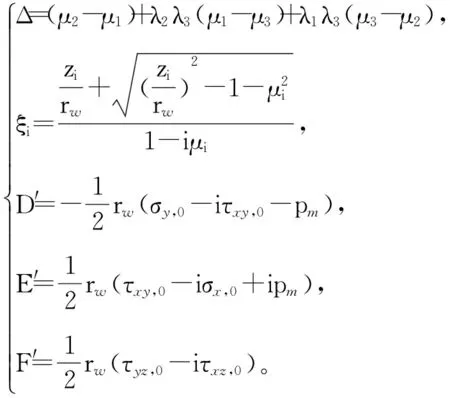
(5)

式中：pm为钻井液液柱压力，MPa；rw为井眼半径，m；μi为与应变协调方程相对应特征方程的特征根；λi为与特征根有关的系数；zi=x+μiy(x=rcosθ,y=rsinθ,i=1,2,3)为复变量；[a]为应变-应力系数矩阵。

为便于井壁应力分析，将井眼垂直坐标系下的应力解(σx,σy,σz,τxy,τxz,τyz)经坐标变换转化为井眼柱坐标系下的应力解(σr,σθ,σz,τrθ,τrz,τθz)，即可得到井周径向应力、周向应力、轴向应力与剪切应力。

3　地层各向异性对井周有效应力分布的影响

基于横观各向同性介质下的井周应力表达式，考虑各弹性力学参数、地应力状态、地层产状和井眼轨迹的影响，编写相应计算程序，可获得任意变化因素下的井周应力分布状态。本文重点分析地层弹性参数各向异性对井周应力的影响，同时将计算结果与各向同性条件下的井周应力进行对比分析。为便于计算，设定页岩地层产状为水平层理，井眼倾斜角为45°，井眼方位角为0°，最大水平地应力为N90°E。Anderson[17]。根据断层类型将地应力状态分为3种，分别为正断层类型地应力(σv>σH>σh)、走滑断层类型地应力(σH>σv>σh)与逆断层类型地应力(σH>σh>σv)，本文以正断层地应力类型为例进行分析。为研究弹性参数各向异性的影响，采用固定层理面法向弹性模量与泊松比而改变层理面方向弹性模量与泊松比的方法进行理论分析(表1)。

3.1井周有效应力分布

3.1.1弹性模量各向异性对井周有效应力分布的影响定义弹性模量的各向异性比为层理面弹性模量与层理面法向弹性模量之比，即RE=Eh/Ev，层理性页岩弹性模量的各向异性比RE≈1～4，因此，取弹性模量各向异性比分别为1、2、3、4。图5为RE=3时的井周应力分布，图中横向为最大水平地应力方位，纵向为最小水平地应力方位。

为分析RE对井周应力的影响，分别对径向、周向与轴向有效应力沿井壁圆周随RE变化的分布与变化幅度进行分析，定义变化幅度为(σRE>1-σRE=1)/σRE=1，因井周正应力沿圆周呈对称分布，只取0°～180°井周方位内的应力数据。同时研究有效应力沿井径方向在不同井周方位(本文选取σH方位与σh方位)处的分布与变化幅度。

表1　页岩地层各计算参数Tab.1　Shale parameters for calculation

因井壁处径向应力等于钻井液液柱压力，故不作特别分析。径向有效应力变化幅度沿井径方向呈增大-减小-增大-减小变化(-3%～10%)(图6(b))，因此，尽管RE对径向有效应力影响较为复杂，但影响幅度较小；周向有效应力在井壁圆周σH与σh方位均随RE增大而减小(图7(b))，其变化幅度在σH方位最大(-145%～-45%)(图7(d))，从而造成当RE≥3时σH方位产生拉伸力，同时，周向有效应力仅在井眼径向方向近井壁(<0.12m)σH方位产生较大影响，远离井壁处应力几乎不变；轴向有效应力沿井壁圆周从σH方位处的随RE增大而增大转变为σh方位处的随RE增大而减小，且σH方位变化幅度稍大于σh方位变化幅度(图8(b))，同时，轴向有效应力变化幅度随距井眼径向距离增大而逐渐减小(图8(d))。因此，RE对井周径向有效应力变化幅度影响最小，对近井壁处σH方位周向有效应力影响最大，表现为随RE增大应力急剧降低，应力状态由压缩变为拉伸。

3.1.2泊松比各向异性影响定义泊松比各向异

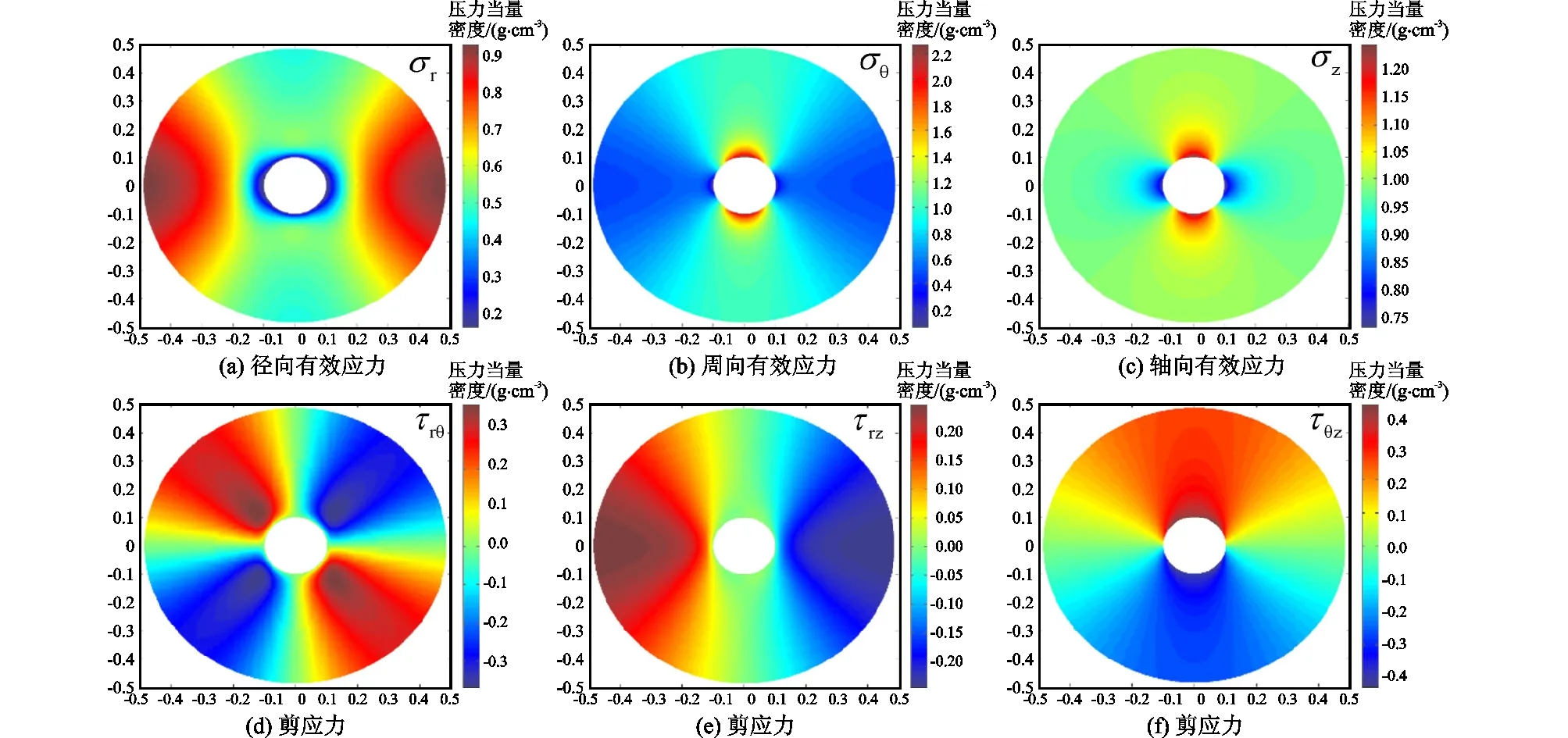
图5　RE=3时的井周有效应力分布Fig.5　Effective stress distribution around wellbore when RE=3

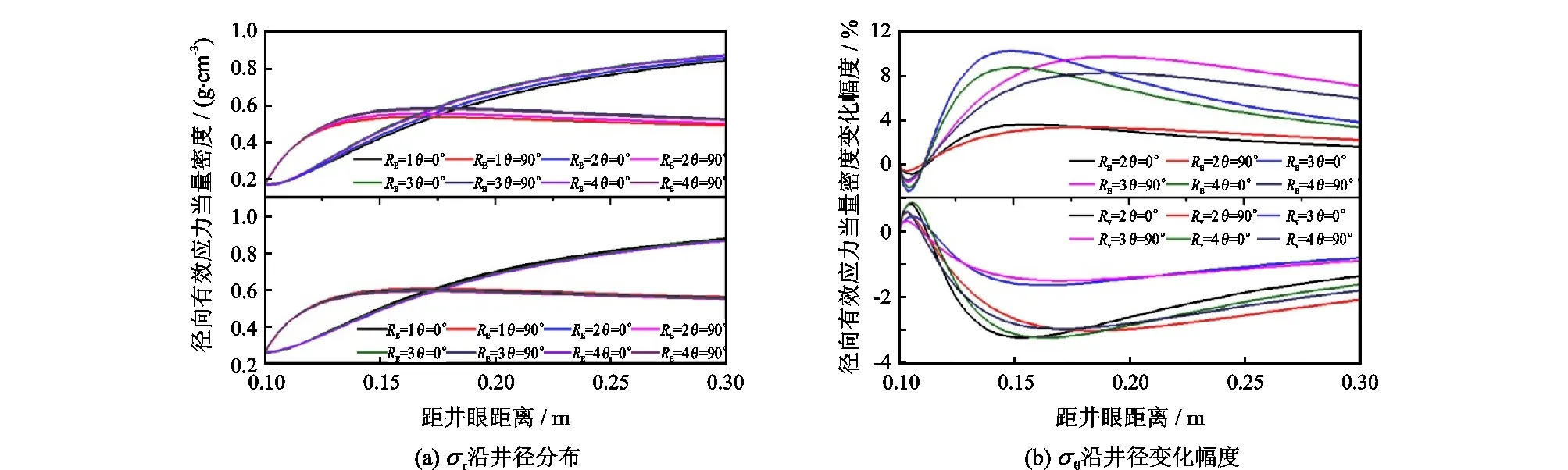
图6　RE与Rv对井周径向有效应力的影响Fig.6　Influences of RE and Rv on radial effective stress distribution around wellbore

性比Rv=νh/νv，取其比值分别为1、2、3、4，井周有效应力随Rv变化规律与RE相似，即Rv对井周径向有效应力影响较小(图6(b))；井周周向有效应力在井眼径向方向近井壁(<0.12m)σH方位产生较大幅度的影响(图7(d))，远离井壁处应力几乎不变，但Rv增减导致的有效应力增减趋势与RE相反。分析表明：径向有效应力和周向有效应力对Rv敏感性弱于RE，而轴向有效应力对Rv敏感性稍强于RE。简言之，RE对井周有效应力分布影响更大。

3.2井周有效主应力分布

页岩井壁稳定性的判断方法是通过分析井周主应力能否满足安全判别准则，井壁失稳包括因剪切作用造成的坍塌破坏与拉伸作用造成的漏失或破裂，因此，本文重点研究井周最大剪切应力与最小有效主应力分布。为直观分析剪切应力大小，运用Tresca准则中的最大剪切应力表达式来描述，即

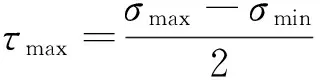
RE=3与Rv=3时的最大剪切应力与最小有效主应力分布分别如图9与图10。其中最大剪切应力发生在σh方位，而最小有效主应力在σH方位处已呈现拉伸状态，σh与σH方位分别对应井壁易坍塌与破裂方位。

3.2.1弹性模量各向异性影响最大剪切应力τmax

沿井壁圆周从σH方位处的随RE增大而增大转变为σh方位处的随RE增大而减小， 其变化幅度在σH方位最大(32%～60%)，而在σh方位较小(-10%～-2%)(图11(b))，但因井壁坍塌首先发生在τmax较大值的σh方位，因此，RE对坍塌压力不会产生较大影响；最小有效主应力σmin在井壁圆周σH方位处随RE增大而急剧减小(图12(d))，应力状态由压缩变为拉伸，易导致形成诱导裂缝，同时，σmin沿井眼径向仅在近井壁(<0.11m)σH方位处产生较大幅度的影响，远离井壁处其变化幅度较小，因此，RE对井壁破裂压力的影响远大于对坍塌压力的影响。

图7　RE与Rv对井周周向有效应力的影响Fig.7　Influences of and RE and Rvon circumferential effective stress distribution around wellbore

图8　RE与Rv对井周轴向有效应力的影响Fig.8　Influences of RE and Rv on axial effective stress distribution around wellbore

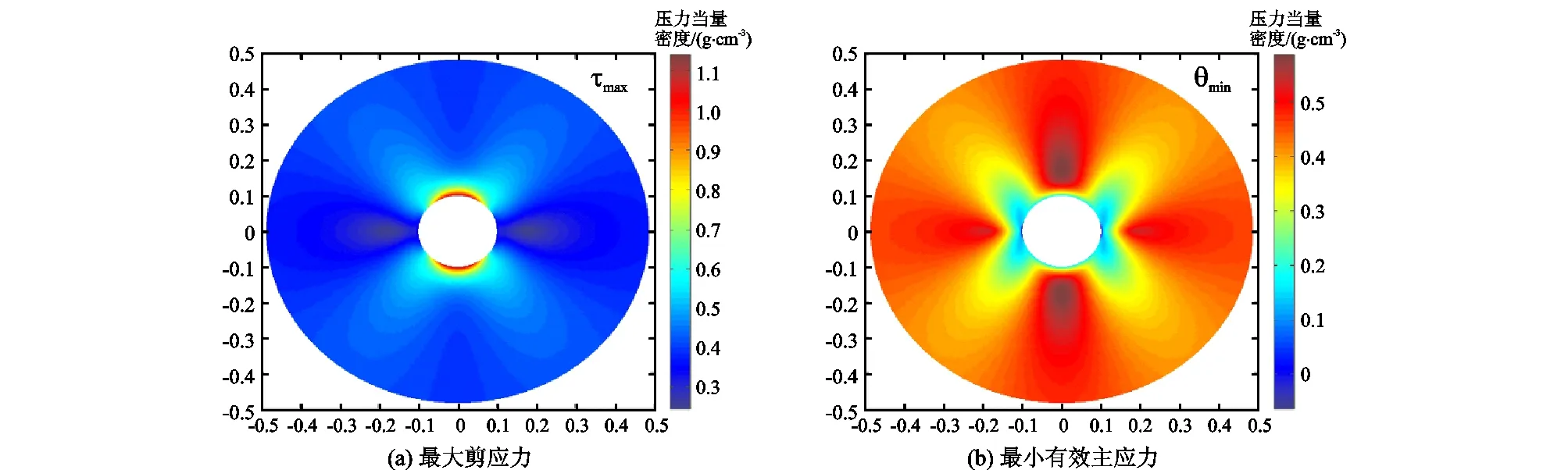
图9　RE=3时最大剪切应力与最小有效主应力分布Fig.9　Max shear stress and min principal effective stress distribution around wellbore when RE=3

图10　Rv=3时最大剪切应力与最小有效主应力分布Fig.10　Max shear stress and min principal effective stress distribution around wellbore when Rv=3

图11　RE与Rv对井周最大剪切应力的影响Fig.11　Influences of RE and Rv on max shear stress distribution around wellbore

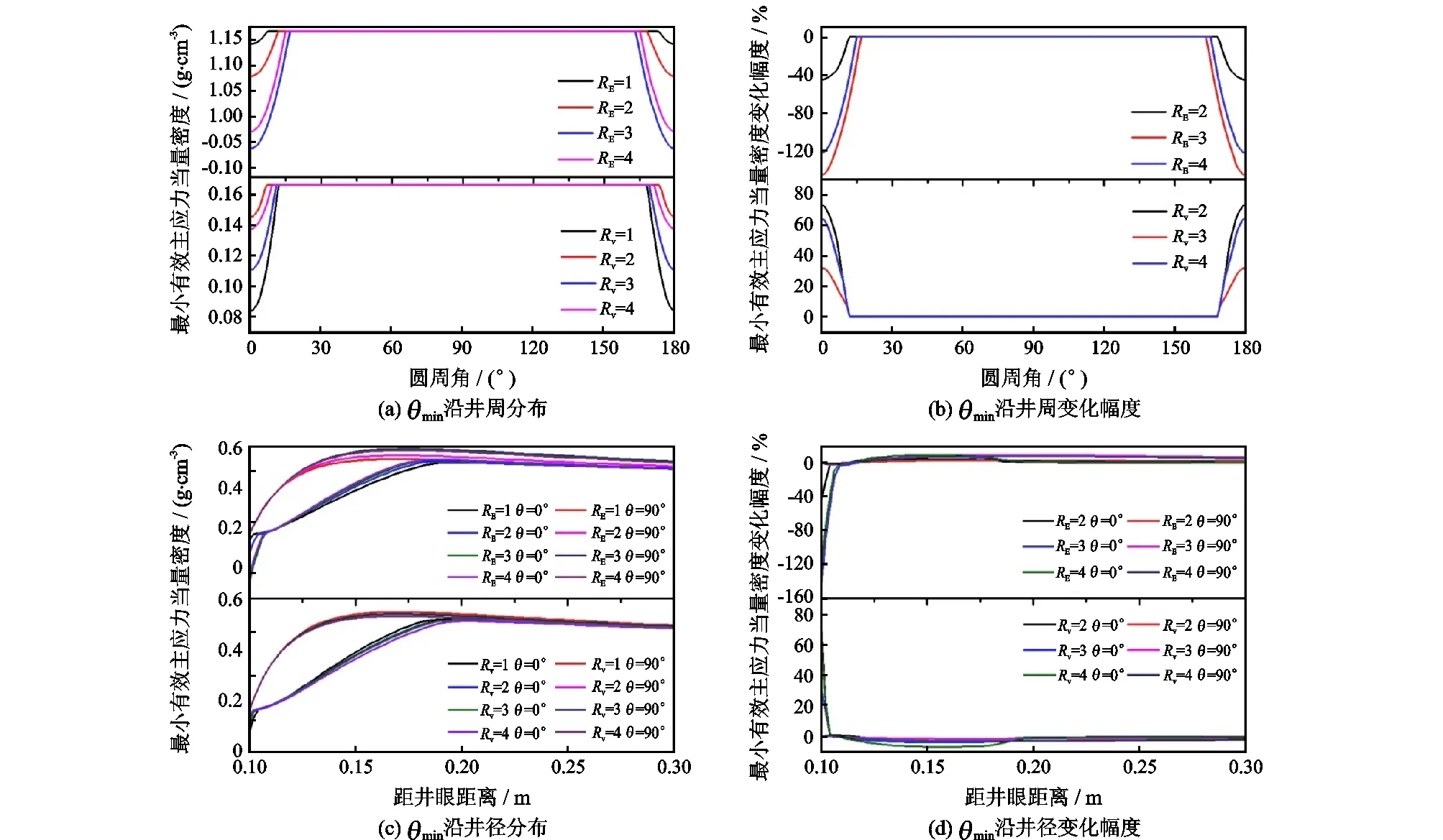
图12　RE与Rv对井周最小有效主应力的影响Fig.12　Influences of RE and Rv on min principal effective stress distribution around wellbore

3.2.2泊松比各向异性影响Rv对井周主应力影响规律与RE的作用具有相似性，即Rv对坍塌压力不会产生明显的影响(图11(d))；Rv仅显著影响近井壁地带σH方位处σmin(图12(d))，但因Rv与RE对最小有效主应力产生的作用相反，Rv增大使最小有效主应力状态由趋于拉伸变为压缩，所以Rv增大不利于井壁发生破裂，反而有利于井壁稳定。因此，坍塌压力与破裂压力受Rv影响均较小，且对Rv敏感性弱于RE。

4　实例分析

CH1井是位于重庆渝东北地区的一口页岩气探井，目的层为水井沱组页岩层，CH1井所在地层为复式向斜构造，地层倾角较大(图1(a))。井壁成像测井表明该井诱导缝较为发育(图13(b))，且通过诱导裂缝产状可判断出钻遇地层最大水平主应力方向主要为近东西向，倾斜角在10°～50°，倾向角以南西西向为主。通过地下岩心力学实验分析，1 295 m处页岩弹性模量Eh为48.89 GPa，Ev为26.31 GPa，泊松比νh为0.29，νv为0.20。测井数据与岩石声发射实验数据表明：地层最大水平主应力为28.6 MPa，水平最小主应力为19.6 MPa，上覆岩层压力为29.9 MPa，取地层倾斜角为45°，倾向角为N105°S。

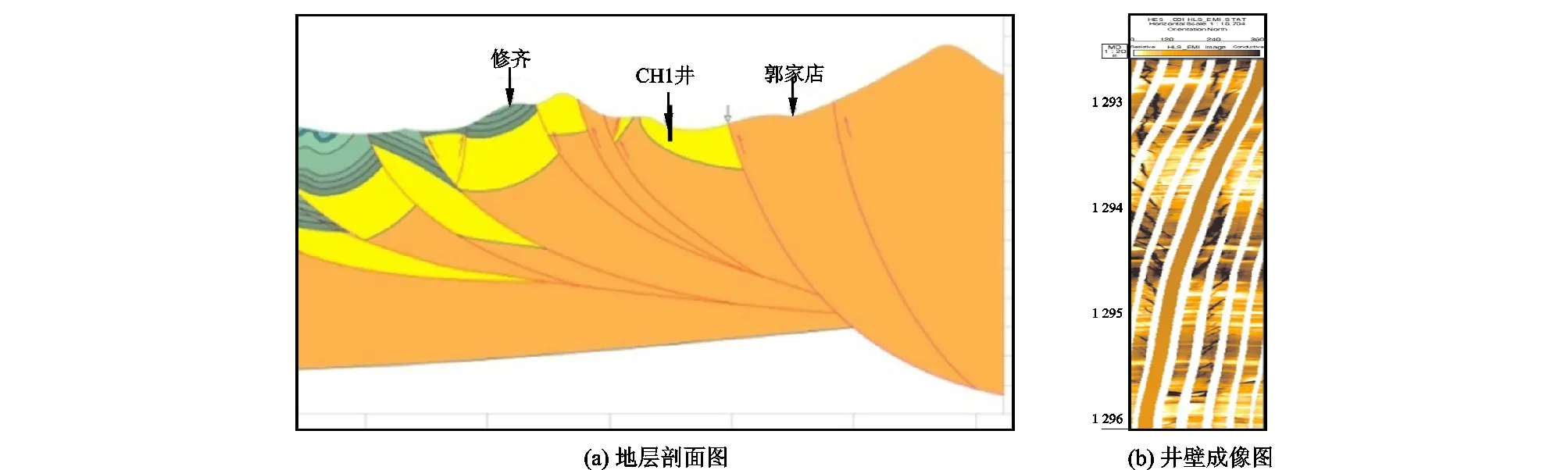
图13　 CH1井地层剖面图与井壁成像Fig.13　Stratigraphic profile and borehole wall logging image of well CH1

运用弹性参数各向异性对井周应力分布影响模型计算CH1井井壁周向有效应力，并与各向同性地层状态下的周向有效应力分布进行对比，图14表明，井周角90°方位附近的周向有效应力为负值，即CH1井井壁承受拉伸应力，而各向同性地层井周周向有效应力均为正值，表明页岩地层弹性参数的各向异性易使井壁形成诱导缝。

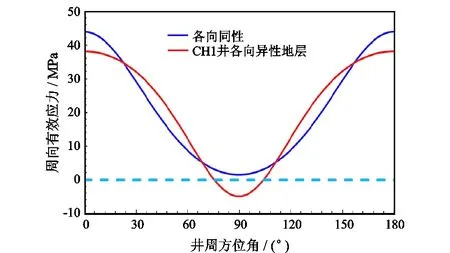
图14　CH1井1 295 m处周向有效应力分布Fig.14　Circumferential effective stress distribution around wellbore of well CH1 at the depth of 1 295 m

5　结　论

(1)井周应力分布对弹性模量各向异性的敏感性强于泊松比各向异性，相同弹性模量与泊松比各向异性比影响下的井周应力分布形态具有相似性，但弹性模量与泊松比各向异性比的增减分别导致的井周应力增减变化相反。

(2)弹性参数各向异性对最大水平地应力方位处应力影响较大，且对周向应力影响最大，致使弹性参数各向异性对井壁破裂压力的影响远大于对坍塌压力的影响，且仅显著影响近井壁处的破裂压力，弹性参数各向异性对井壁坍塌压力影响不大。

[1]赵靖舟,方朝强,张洁,等.由北美页岩气勘探开发看我国页岩气选区评价[J].西安石油大学学报(自然科学版),2011,26(2):1-7.

ZHAO Jingzhou,FANG Chaoqiang,ZHANG Jie,et al.Evaluation of China shale gas from the exploration and development of North America shale gas[J].Journal of Xi'an Shiyou University(Natural Science Edition),2011,26(2):1-7.

[2]衡帅,杨春和,张保平,等.页岩各向异性特征的试验研究[J].岩土力学,2015,36(3):609-616.

HENG Shuai,YANG Chunhe,ZHANG Baoping,et al.Experimental research on anisotropic properties of shale[J].Rock and Soil Mechanics,2015,36(3):609-616.

[3]王倩,王鹏,项德贵,等.页岩力学参数各向异性研究[J].天然气工业,2012,32(12):62-65,130.

WANG Qian,WANG Peng,XIANG Degui,et al.Anisotropic property of mechanical parameters of shales[J].Natural Gas Industry,2012,32(12):62-65,130.

[4]崔杰,焦永树,曹维勇,等.各向异性地层中井孔周围应力场的研究[J].工程力学,2011,28(7):31-36.

CUI Jie,JIAO Yongshu,CAO Weiyong,et al.A study on the stress field around a borehole in anisotropic formation[J].Engineering Mechanics,2011,28(7):31-36.

[5]李军,柳贡慧,陈勉.正交各向异性地层井壁围岩应力新模型[J].岩石力学与工程学报,2011,30(12):2481-2485.

LI Jun,LIU Gonghui,CHEN Mian.New model for stress of borehole surrounding rock in orthotropic formation[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(12):2481-2485.

[6]韩昌瑞,白世伟,张波.正交各向异性岩体钻孔周围应力分布的应力变分法分析[J].岩土力学,2007,28(12):2593-2597.

HAN Changrui,BAI Shiwei,ZHANG Bo.Analysis of stress distribution near borehole in orthotropic rockmass with stress calculus of variations[J].Rock and Soil Mechanics,2007,28(12):2593-2597.

[7]HAKALA M,KUULA H,HUDSON J A.Estimating the transversely isotropic elastic intact rock properties for in situ stress measurement data reduction:a case study of the Olkiluoto mica gneiss,Finland[J].International Journal of Rock Mechanics and Mining Sciences,2007,44(1):14-46.

[8]卢运虎,陈勉,袁建波,等.各向异性地层中斜井井壁失稳机理[J].石油学报,2013,34(3):563-568.

LU Yunhu,CHEN Mian,YUAN Jianbo,et al.Borehole instability mechanism of a deviated well in anisotropic formations[J].Acta Petrolei Sinica,2013,34(3):563-568.

[9]陈平,马天寿,夏宏泉.含多组弱面的页岩水平井坍塌失稳预测模型[J].天然气工业，2014,34(12):87-93.

CHEN Ping,MA Tianshou,XIA Hongquan.A collapse pressure prediction model of horizontal shale gas wells with multiple weak planes[J].Natural Gas Industry,2014,34(12):87-93.

[10] 马天寿,陈平.页岩地层中孔隙热弹性井眼稳定力学模型[J].岩石力学与工程学报,2015,34(s2):3613-3623.

MA Tianshou,CHEN Ping.Porothermoelastic mechanical model of wellbore stability shale formation[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(s2):3613-3623.

[11] TIEN Y M,KUO M C.A failure criterion for transversely isotropic rocks[J].International Journal of Rock Mechanics and Mining Sciences,2001,38(3):399-412.[12] KHAN S,ANSARI S A,HAN H,et al.Importance of shale anisotropy in estimating in-situ stresses and wellbore stability analysis in Horn River Basin[C].Canadian Unconventional Resources Conference.Society of Petroleum Engineers,2011.

[13] AADNOY B S.Modeling of the stability of highly inclined boreholes in anisotropic rock formations (includes associated papers 19213 and 19886 )[J].SPE Drilling Engineering,1988,3(3):259-268.

[14] 裴正林.层状各向异性介质中横波分裂和再分裂数值模拟[J].石油地球物理勘探,2006,41(1):17-25.

PEI Zhenglin.Numeric simulation of S-wave splitting and second splitting in layered anisotropic media[J].Oil Geophysical Prospecting,2006,41(1):17-25.

[15] 祁斌,夏宏泉,房国庆,等.基于偶极横波测井的地层各向异性研究[J].测井技术,2008,32(5):412-415.

QI Bin,XIA Hongquan,FANG Guoqing,et al.On stratum anisotropy based on DSI log information[J].Well Logging Technology,2008,32(5):412-415.

[16] LEKHNITSKII S G.Elasticity Theory of Anisotropic Bodies[M].Moscow :Nauka,1977.

[17] ANDERSON E M.The Dynamics of Faulting and Dyke Formation with Applications to Britain[M].Edinburgh:Oliver and Boyd,1951.

责任编辑：王辉

Effect of Anisotropy of Elastic Parameters of Shale Formation on Stress Distribution Around Wellbore

CAO Wenke,DENG Jin'gen,YU Baohua,LIU Wei,LI Yang

(State Key Laboratory of Petroleum Resource and Prospecting,China University of Petroleum (Beijing),Beijing 102249)

In order to analyze the stress distribution around the borehole in stratification shale and its influence on the stability of the borehole,a model for calculating the stress distribution around the borehole in stratification shale was established based on the anisotropic characteristics of shale mechanical parameters and the constitutive relations of transversely isotropic material,the influence law of the anisotropy of the elastic parameters of shale formation on the stress distribution around borehole is obtained by comparing the calculation result with the stress distribution around the borehole in transversely isotropic shale,and the stability of the borehole in the stratification shale was evaluated.It is shown that,the stress distribution around borehole is more sensitive to the anisotropy of Young's modulus than that of Poisson's ratio;the stress distribution form around borehole is similar under the same anisotropy degree of Young's modulus and Poisson's ratio,but the variation tendency of the stress distribution around borehole is opposite to the variation tendency of the anisotropy ratio of Young's modulus to Poisson's ratio;the influence of the anisotropy of elastic parameters on borehole fracture pressure is much greater than that on borehole collapse pressure,and the anisotropy of elastic parameters significantly influences the rock fracture pressure near wellbore.

stress distribution around borehole;transversely anisotropy shale;wellbore stability

2016-04-16

国家自然科学基金(编号：U1262201)；国家自然科学基金(编号：PRP/indep-4-1311)

曹文科(1984-)，男，博士研究生，主要从事岩石力学与井壁稳定性研究。E-mail:caowenk@hotmail.com

10.3969/j.issn.1673-064X.2016.05.004

TE21

1673-064X(2016)05-0027-09

A