基于蒙特卡洛法的埋地悬空管道结构可靠度分析

白路遥，施 宁，李亮亮，马云宾，蔡永军，姬 江

(1.中国石油管道科技研究中心 油气管道输送安全国家工程实验室，河北 廊坊 065000；2.西北石油管道公司 质量安全环保部，陕西 西安 710018)



基于蒙特卡洛法的埋地悬空管道结构可靠度分析

白路遥1，施 宁1，李亮亮1，马云宾1，蔡永军1，姬 江2

(1.中国石油管道科技研究中心 油气管道输送安全国家工程实验室，河北 廊坊 065000；2.西北石油管道公司 质量安全环保部，陕西 西安 710018)

为了计算埋地悬空管道的可靠度，基于蒙特卡洛统计模拟法，结合受力特征，建立了埋地悬空管道结构可靠度计算模型并计算了某黄土湿陷区埋地悬空管道的可靠度。为了描述不同影响因素对管道可靠度的影响程度，从管道失效概率的角度定义了参数的敏感性指标，对管道设计中经常涉及的管道外径、壁厚、埋深、悬空长度、屈服强度、温度差、管道内压7个随机变量进行了敏感性分析，讨论了参数的变化对管道可靠度的影响。结果表明：建立的埋地悬空管道可靠度计算模型能够对埋地悬空管道的可靠度进行计算；管道的悬空长度对可靠性影响程度最大，最大程度减小管道的悬空长度，适当减小管道埋深，降低管道内压，增大管道壁厚和屈服强度，有助于提高管道的可靠度。

蒙特卡洛法；埋地悬空管道；结构可靠度；敏感性分析；黄土湿陷

白路遥，施宁，李亮亮，等.基于蒙特卡洛法的埋地悬空管道结构可靠度分析[J].西安石油大学学报(自然科学版)，2016，31(5):48-52,59.

BAI Luyao，SHI Ning，LI Liangliang，et al.Structure reliability analysis of buried suspended pipeline based on Monte-Carlo method[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(5):48-52,59.

引　言

长输油气管道沿线地理环境复杂，在地质灾害的影响下，埋地油气管道往往发生管沟侵蚀，甚至出现一定长度的裸露悬空段。此时，在管道自身和内部流体介质的重力作用下，悬空管道会发生变形，较大的变形会导致管道失效，造成严重的事故。 鉴于此，国内外许多学者从不同角度对悬空管道的安全进行了大量研究。魏孔瑞等[1]依据强度理论建立了悬空管道沉降失效评估模型；王峰会等[2]针对穿过黄土高原地区的西气东输管道工程，基于弹性地基梁理论建立了管道在地基塌陷时的力学模型；张鹏等[3]对地表冲沟条件下的悬空管道进行了仿真计算；王同涛等[4]建立了黄土湿陷段悬空管道受力的弹塑性地基模型；杨毅等[5]基于强度理论，对水流冲击作用下输油管道悬空管段进行了应力计算。以上讨论大多依据数值模拟和强度理论对悬空管道的安全状态进行校核，而对悬空管道可靠性研究甚少。

事实上，悬空管道的力学模型以及影响因素都具有较大的不确定性，而现有管道可靠性分析中还缺乏埋地悬空管道结构可靠度的计算方法。近年来，在油气管道行业，可靠度理论已经广泛应用于大型油气管网系统可靠性评价[6-7]、管道腐蚀缺陷的安全评价[8-9]、管道单元可靠性评价[10-11]以及管道线路的结构可靠度评价[12-13]等诸多方面。因此，可以将可靠度理论应用于悬空管道的结构可靠度计算。蒙特卡洛法[14]是目前计算结构可靠度的常用方法之一，该方法计算的收敛速度与随机变量的维数无关，无需将极限状态函数线性化和随机变量“当量正态化”，而且数值模拟的误差也容易确定，常常用来计算结构失效概率，在结构可靠度模拟领域应用广泛[15]。因此，本文基于结构可靠度理论，在悬空管道力学模型的基础上，建立管道的失效功能函数并确定随机变量，采用蒙特卡洛法对埋地悬空管道的可靠度进行评价，为工程设计与管理提供理论依据。

1　埋地悬空管道失效功能函数

1.1力学模型

当黄土湿陷时，管道下方土层下陷或流失，造成管道局部悬空。由于悬空段受均布荷载作用，且管道两段受到未塌陷土层的弹性支撑，根据Winker假设[6]，一般将这种管道的受力模型视为两端受弹性支撑的变形梁模型[4，7]，如图1所示。管道两端为弹性支撑，在均布荷载q的作用下发生变形，且挠曲线关于最大挠度处c-c线对称，同时该悬空管段两端受轴向力N0、管道埋入端弯矩M0、悬空管段均布荷载q作用下而产生的剪力Q0的共同作用。

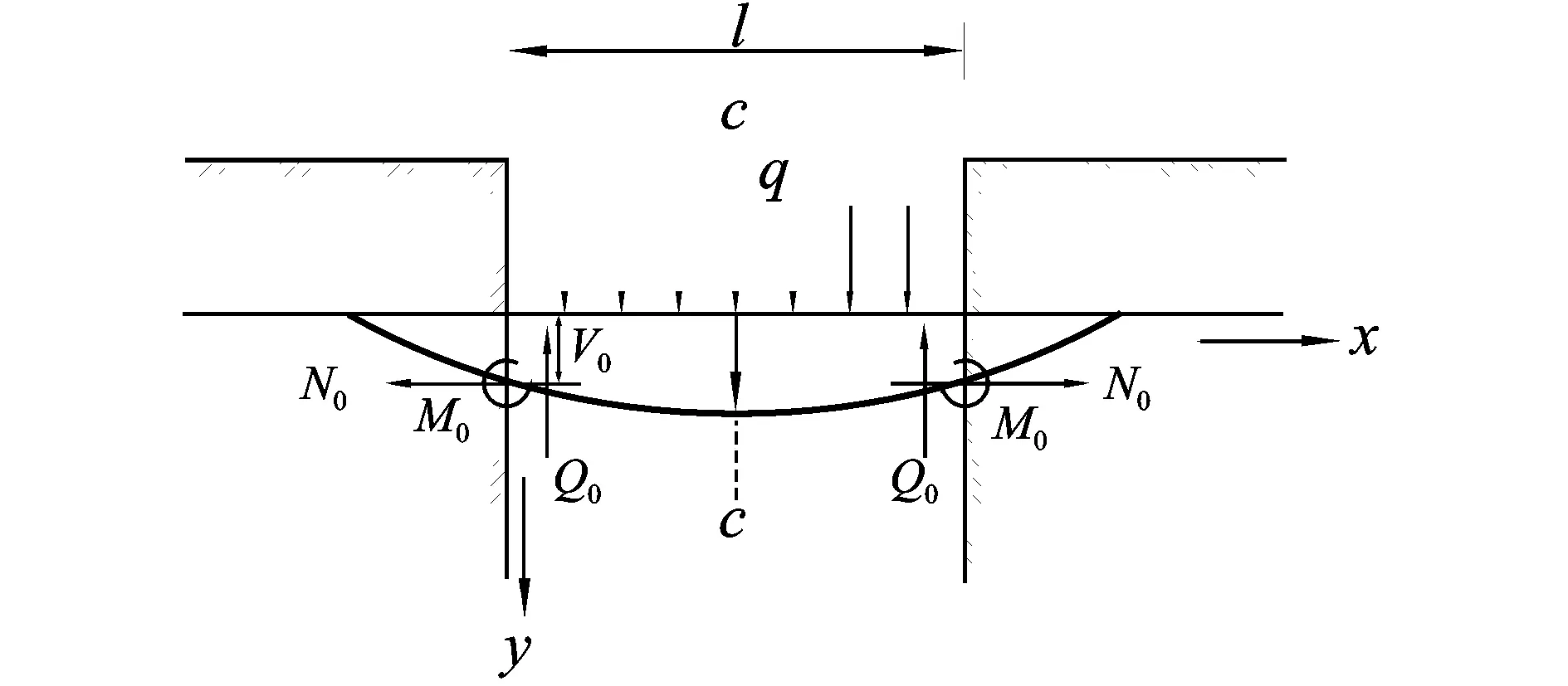
图1　悬空管道的力学模型Fig.1　Mechanical model of suspended pipeline

由图1的力学模型求得管道的挠曲线微分方程为

(1)

管土交界处管道截面弯矩为

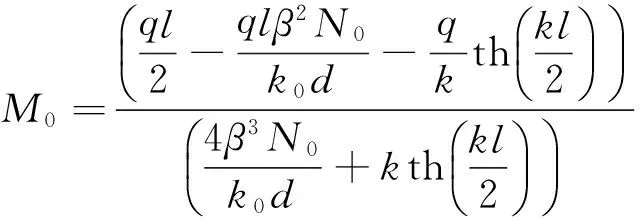
(2)

其中，

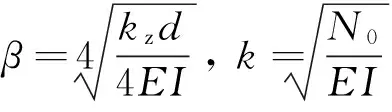
悬空管道任一截面上的弯矩为

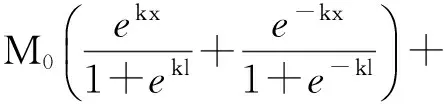
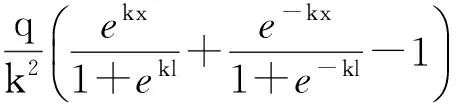
(3)

土中管道对悬空段的水平拉力为

(4)

其中，均布荷载q包括管道自重、输送介质重量和管道上方土层重量。

(5)

式中：E为管材弹性模量，MPa;I为管道截面惯性矩，m4；ν0为管土交界处管道挠度，m；d为管道内径，mm;D为管道外径，m；l为悬空管道长度，m;kz为基床系数；c为土的粘结力，kPa；k0为静止土压力系数；φ为土的摩擦角；γ为土的容重，kN/m3；l′为管道深入土体中的可变形长度，取1.5l，m;ρp为管材密度，kg/m3；pa为管道内压，MPa；h为管道埋深，m；ρs为管道上方覆土密度，kg/m3。

1.2应力模型

悬空管道在多种荷载作用下产生了轴向应力、环向应力与径向应力。其中管道轴向应力为水平拉力所产生的轴向应力与管道内压、均布荷载、温度差引起的轴向应力之和。因此，管道轴向总应力为

(6)

管道的环向应力与径向应力由管道内压引起，一般将管道视为薄壁筒，忽略径向应力，由材料力学可得管道的环向应力为

(7)

式中：t为管道壁厚，mm；W为管道抗弯截面系数，m3；α为管材热胀系数，℃-1；Ss为管壁横截面面积，m2；其他参数同前。

1.3失效功能函数

对于在各种载荷作用下的悬空管道，其结构应力是判断管道可靠与否的重要指标，当管道的等效应力超过管道的屈服应力时管道失效。根据Mises强度理论，悬空管道的失效功能函数可表示为

(8)

式中：σs为管道屈服应力，MPa；σ1为管道轴向总应力，MPa；σ2为管道环向应力，MPa；σ3为管道径向应力，MPa。当G(X)>0时，表示管道能够正常运行，即处于可靠状态；当G(X)<0时，管道不能正常工作，即管道处于失效状态；当G(X)=0时，管道处于临界状态。根据可靠性理论，埋地悬空管道的可靠性就是求G(X)>0的概率。

2　基于蒙特卡洛法的可靠度分析

本文采用蒙特卡洛法对悬空管道结构可靠度进行分析，如图2所示。首先，根据已建立的悬空管道力学模型分析管道所受载荷并根据管道应力失效准

则建立失效功能函数，然后确定功能函数中的随机变量及其概率分布，最后根据随机变量的概率分布随机抽样得出样本值并统计管道安全，如此重复，直到完成预定的次数或达到一定的预定准则，以此计算可靠度。基于蒙特卡洛法计算的悬空管道可靠度可表示为

(9)

图2　基于蒙特卡洛法的结构可靠度分析流程Fig.2　Process of structural reliability analysis based on Monte Carlo method

悬空管道可靠性分析的重要内容之一是确定随机变量及其概率分布。根据悬空管道的受力特征，可靠性分析所涉及的随机变量包括管道的几何参数、材料参数和荷载参数。表1给出了可靠度计算所涉及的随机变量及其概率分布。根据管道的设计参数及设计工况，管道外径、壁厚、埋深、屈服强度、内压均为正态分布。其中，管道悬空长度分布类型的确定相对较难，其影响因素包括地质条件、管道周边环境、气候与水文条件等多种因素，通过管沟黄土湿陷机理计算黄土湿陷概率以及管道悬空长度的概率分布比较困难。因此，在对管道悬空长度分布信息掌握不够的情况下，依据机会均等原则，假定管道的悬空长度是0到可能最大值之间的均匀分布[9]。

表1　随机变量及其概率分布Tab.1　Random variables and their probability distribution types

3　实例分析

3.1可靠度计算

利用上述模型对某湿陷性黄土地区埋地天然气管道进行结构可靠度分析，模型输入参数共有3种分布类型，分别为正态分布、均匀分布和常数。表2和表3分别给出了模型中随机变量与常量的统计参数，虽然统计参数之间可能具有一定的相关性，但目前由于对参数之间的关系认识不够，因此假定模型的随机变量相互独立。基于算例参数，本文利用Matlab软件采用蒙特卡洛法进行106次随机抽样模拟，求得管道可靠度为0.998 33。

表2　算例随机变量Tab.2　Random variables in example

表3　算例常量Tab.3　Constants in example

3.2参数的敏感性分析

根据悬空管道的力学模型可知，管道悬空后轴向拉应力过大是造成管道失效的主要原因，在参数的敏感性分析中应重点考虑轴向应力所含的参数。此外，管道设计过程中，为了满足下游用户需求同时保证管道可靠性，需要确定管道内压、埋深、内径、壁厚等参数。因此，进行这些参数敏感性分析对管道的风险控制具有重要意义。由于根据蒙特卡洛法定义敏感性指标比较复杂，且无法用解析法求解，故本文采用计算基本事件临界重要度的方法进行参数的敏感性分析，将敏感性指标定义为[8,18]

(10)

式中：Ci为基本随机变量；ΔCi为随机变量的变化；Pr为结构的可靠度；ΔPr为对应ΔCi引起可靠度的变化。αi越大，表示随机变量Ci对可靠度的影响越

大，换言之，Ci的微小变化将引起可靠度较大的变化。

根据算例，本文将各随机变量由算例值增大至20%，变异系数保持不变，分析埋地悬空管道可靠度的变化趋势(图3)。由图3可见，增大管道外径、埋深、悬空长度、内压和温度差，管道可靠度呈现逐渐减小的趋势，而增大管道壁厚、屈服强度，管道可靠度逐渐增大。其中，管道悬空长度的变化对可靠度的影响程度最大，当管道悬空长度由30 m增大至36 m时，管道可靠度由0.983下降至0.876。此外，由图3可以看出，可靠度与随机变量变化的关系具有明显的非线性特征。为了进一步确定随机变量对管道可靠度的影响程度，在随机变量的变化过程中，根据式(10)对埋地悬空管道的参数进行敏感性分析，得到参数敏感性指标的最大值(表4)。由表4可见，管道悬空长度的敏感性指标最大，埋深、内压、屈服强度、壁厚和外径等参数的敏感性指标相近，温度差的敏感性指标最小，即悬空长度的变化会引起管道可靠度发生较大变化。因此，最大程度地减小悬空管道长度，增加管道的强度，修建管道保护结构(如管道碳纤维强固结构[3])，将长悬空管道分割为若干短悬空管道，适当减小管道埋深和内压，同时适当增大管道壁厚和屈服强度，则有助于提高管道的可靠度。

图3　随机变量的变化对可靠度的影响Fig.3　Influence of the change of random variables on reliability表4　参数敏感性指标最大值Tab.4　Maximum value of parameter sensitivity indexes

参数名称外径壁厚埋深悬空长度屈服强度内压温度差αmax10.5514.4018.8931.8416.1917.551.67

4　结　论

(1)根据蒙特卡洛统计模拟法，结合埋地悬空管道的受力特征，建立的可靠度计算模型能够对埋地悬空管道的可靠度进行计算，为管道管理者提供决策依据。

(2)模型中各参数的变化对管道可靠性影响程度不同，其中，管道的悬空长度对可靠性影响程度最大。最大程度减小管道的悬空长度，适当减小管道埋深、降低管道内压，同时增大管道壁厚和屈服强度，有助于提高管道的可靠度。

[1]魏孔瑞，姚安林，张照旭，等.埋地油气管道悬空沉降变形失效评估方法研究[J].中国安全科学学报，2014,24(6):68-73.

WEI Kongrui,YAO Anlin,ZHANG Zhaoxu,et al.Study on method for assessing failure of settlement and deformation of buried oil and gas suspended pipelines[J].China Safety Science Journal,2014,24(6):68-73.

[2]王峰会，赵新伟，王沪毅.高压管道黄土塌陷情况下的力学分析与计算[J].油气储运，2004，23(4)：6-8.

WANG Fenghui,ZHAO Xinwei,WANG Huyi.Mechanical analysis and calculation of high pressure pipeline under collapse of loess[J].Oil & Gas Storage and Transportation，2004，23(4)：6-8.

[3]张鹏，魏韡，崔立伟，等.地表冲沟条件下悬空管道的力学模型与延寿分析[J].天然气工业，2014,34(4):142-148.

ZHANG Peng,WEI Wei,CUI Liwei,et al.A mechanical model and life extension analysis of the suspended pipelines under the condition of geological gulch[J].Natural Gas Industry,2014,34(4):142-148.

[4]王同涛，闫相祯，杨秀娟.基于弹塑性地基模型的湿陷性黄土地段悬空管道受力分析[J].中国石油大学学报(自然科学版)，2010,34(4)：113-118.

WANG Tongtao,YAN Xiangzhen,YANG Xiujuan.Force analysis of suspended pipeline loess areas based on elastic-plastic foundation model[J].Journal of China University of Petroleum(Edition of Natural Science),2010,34(4)：113-118.

[5]杨毅，闫宝东，廖柯熹.输油管道悬空管段应力计算[J].石油学报,2011,32(5):911-914.

YANG Yi,YAN Baodong,LIAO Kexi.Computing analysis of the suspended segment stress of oil pipelines[J].Acta Petrolei Sinica,2011,32(5):911-914.

[6]黄维和.大型天然气管网系统可靠性[J].石油学报，2013，34(2):401-404.

HUANG Weihe.Raliability of large-scale natural gas pipeline network[J].Acta Petrolei Sinica,2013，34(2):401-404.

[7]艾慕阳.大型油气管网系统可靠性若干问题探讨[J].油气储运，2013,32(12)：1265-1270.

AI Muyang.Discussion on issues regarding the reliability of large-scale oil and gas pipeline network systems[J].Oil & Gas Storage and Transportation，2013,32(12)：1265-1270.

[8]韩文海，周晶.腐蚀海底管道可靠性分析[J].石油学报，2015,36(4)：516-520.

HAN Wenhai,ZHOU Jing.Reliability analysis of corroded subseapipeline[J].Acta Petrolei Sinica,2015,36(4)：516-520.

[9]邵煜，张土乔，俞亭超.考虑腐蚀的埋地灰口铸铁管失效预测及可靠度分析[J].浙江大学学报(工学版),2010,44(1):160-165.

SHAO Yu,ZHANG Tuqiao,YU Tingchao.Failure prediction and reliability analysis of buried grey cast iron water mains considering corrosion[J].Journal of Zhejiang University (Engineering Science),2010,44(1):160-165.

[10] 张宗杰，谢青青，文江波，等.干线天然气管道运行可靠性评价方法[J].油气储运，2014,33(8)：807-812.

ZHANG Zongjie,XIE Qingqing,WEN Jiangbo,et al.Reliability evaluation method for gas trunk line[J].Oil & Gas Storage and Transportation，2014,33(8)：807-812.

[11] 李俊山.天然气压缩机可靠性分析[D].成都：西南石油学院，2005.

LI Junshan.Reliability Analysis of Natural Gas Compressor[D].Chengdu:Southwest Petroleum Institute,2010.

[12] 温凯，张文伟，宫敬，等.天然气管道可靠性计算方法[J].油气储运，2014,33(7)：729-733.

WEN Kai,ZHANG Wenwei,GONG Jing,et al.Computation of gas pipeline reliability[J].Oil & Gas Storage and Transportation，2014,33(7)：729-733.[13] 李军，秦朝葵，马洪敬.城市高压燃气管道的结构可靠性分析[J].中国安全生产科学技术，2014,10(11)：113-118.

LI Jun,QIN Chaokui,MA Hongjing.Analysis on structural reliability of urban high-pressure gas pipeline[J].Journal of Safety Science and Technology,2014,10(11)：113-118.

[14] 赵国藩，金伟良，贡金鑫.结构可靠度理论[M].北京：中国建筑工业出版社，2000：79-90.

ZHAO Guofan，JIN Weiliang，GONG Jinxin.Structural Reliability Theory[M].Beijing:China Architecture & Building Press,2000：79-90.

[15] 吴迪.基于马尔可夫链蒙特卡洛法的天然气管道腐蚀可靠性研究[D].西安：西安建筑科技大学，2013.

WU Di.Study on Corrosion Reliability of Gas Pipeline Based on Markov Chain Monte Carlo Method[D].Xi'an:Xi'anUniversity of Architecture and Technology,2013.

[16] 龙驭球.弹性地基梁的计算[M].北京：高等教育出版社，1989:6-23.

LONG Yuqiu.Calculation of the Elastic Foundation Beam[M].Beijing:Higher Education Press,1989：6-23.

[17] 罗金恒，赵新伟，王峰会，等.地质灾害下悬空管道的应力分析及计算[J].压力容器,2006,23(6):23-26.

LUO Jinheng,ZHAO Xinwei,WANG Fenghui,et al.Stress analysis and calculation of suspended pipeline due to geotechnical hazards[J].Pressure Vessel Technology,2006,23(6):23-26.

[18] 章国栋，陆延孝，屠庆慈，等.系统可靠性与维修性的分析与设计[M].北京：北京航空航天大学出版社，1990：14-33.

ZHANG Guodong,LU Yanxiao,TU Qingci,et al.Analysis and Design of System Reliability and Maintenance[M].Beijing:Beijing University of Aeronautics and Astronautics Press,1990：14-33.

责任编辑：贺元旦

Structure Reliability Analysis of Buried Suspended Pipeline Based on Monte-Carlo Method

BAI Luyao1，SHI Ning1，LI Liangliang1，MA Yunbin1，CAI Yongjun1，JI Jiang2

(1.National Engineering Laboratory for Oil & Gas Pipeline Transportation Safety,Pipeline Science and Technology Research Center of CNPC,Langfang 065000,Hebei,China;2.Quality Safety and Environmental Protection Department,Northwest Petroleum Pipeline Company,Xi'an 710018,Shaanxi,China)

In order to calculate the reliability of buried suspended pipeline,a structural reliability model for the buried suspended pipeline was established with Monte Carlo method based on the stress characteristics of the buried suspended pipeline.The reliability of the buried suspended pipeline in a loess collapse region was calculated using the model.In addition,in order to study the influences of different factors on the reliability of pipeline,a sensitivity index is defined in the view of failure probability.Meanwhile,the sensitivity of the random variables usually used in pipeline design,such as external diameter,wall thickness,buried depth,suspended length,yield strength,temperature difference,to the reliability of the buried suspended pipeline is analyzed.The analysis results show that the established reliability calculation model can be used for calculating the reliability of buried suspended pipeline.The suspended length of pipeline is the most sensitive parameter,and therefore it should be reduced on the maximum degree.To appropriately reduce buried depth and internal pressure and to appropriately increase wall thickness and yield strength will be helpful to improving the reliability of pipeline.

Monte Carlo method;buried suspended pipeline;structural reliability;sensitivity analysis;loess collapse

2016-03-10

中国石油天然气集团公司科研项目“大型天然气管网系统可靠性研究”(编号：2014B-3411)

白路遥(1986-)，男，工程师，主要从事管道地质灾害评价与防护技术研究。E-mail: bailuyao@petrochina.com.cn

10.3969/j.issn.1673-064X.2016.05.007

TE832.3

1673-064X(2016)05-0048-05

A