随机截尾数据下的液压泵故障分布的两参数威布尔分布模型*

熊申辉，胡良谋，胡　飞，曹克强，景　涛，高　斌

(1. 空军后勤部 司令部，北京　100720；2. 空军工程大学 航空航天工程学院，西安　710038；3. 广州军区 空军装备部，广州　510071)



随机截尾数据下的液压泵故障分布的两参数威布尔分布模型*

熊申辉1，胡良谋2，胡飞3，曹克强2，景涛2，高斌2

(1. 空军后勤部 司令部，北京100720；2. 空军工程大学 航空航天工程学院，西安710038；3. 广州军区 空军装备部，广州510071)

液压泵在使用阶段的可靠性能最真实地反映产品的实际可靠性水平和薄弱环节，其可靠性数据具有随机截尾特性，因此其可靠性数据分析面临着诸多困难。首先提出了一种基于随机截尾数据的两参数威布尔分布的建模方法，并将其应用于某型液压泵的可靠性数据分析，最后进行了仿真试验研究。仿真试验结果表明，基于平均秩次法的液压泵两参数威布尔分布模型比基于残存比率法的两参数威布尔分布模型更为精确，同时验证了威布尔分布的优越性。研究成果为基于随机截尾数据的液压泵提供了一种更为精确的可靠性分析方法。

液压泵；随机截尾数据；两参数威布尔分布；平均秩次法；残存比率法

0　引言

液压泵[1-3]是飞机液压传动与控制系统中的能源部件，它的作用是向系统提供一定压力和流量的油液。从能量转换的观点来说，液压泵是把机械能转换为液压能的装置。为了指导使用维护工作，迫切需要进行液压泵的可靠性分析。

液压泵在使用阶段的可靠性数据分析具有重要的研究意义。这是因为液压泵在使用阶段反映的使用及环境条件最真实，参与评估的液压泵数量较多，因此在该阶段收集的可靠性数据极为珍贵，它能最真实地反映液压泵的实际可靠性水平和薄弱环节，对设计和制造的评价最权威，其可靠性数据分析结果是可靠性工作的最终检验，也是今后开展新型液压泵可靠性设计的最有价值的参考。

在实际工作中，同类型的液压泵投入使用的时间不同；观测者记录数据时除故障时间外，还有一些液压泵统计时仍在完好地工作；以及使用中途液压泵会因某种原因转移他处等，这些原因都导致了液压泵在使用阶段收集的可靠性数据具有随机截尾的特性。随机截尾型可靠性数据由于其独特的数据特征，其可靠性分析面临着诸多困难和难点，相关技术的研究与开发一直都是可靠性工程领域的研究热点和难点。

威布尔分布[4-5]是一种连续分布，它能够描述航空产品各种类型失效数据的分布规律，其优点在于它对各种类型的试验数据具有极强的适应能力，能够充分地描述失效机理。因此在可靠性分析方面，威布尔分布成为近年来研究最为广泛的参数模型。

本文主要研究随机截尾数据下的两参数威布尔分布的建模方法，并将其应用于某型液压泵的可靠性数据分析。

1　两参数威布尔分布模型

两参数威布尔分布的分布函数为[5-10]

(1)

式中：η称为尺度参数，m称为形状参数。

2　随机截尾数据下的两参数威布尔分布模型

两参数威布尔分布的未知参数包括尺度参数和形状参数。只有在确定这两个参数后，才能利用分布模型计算各个可靠性指标。

2.1随机截尾数据下的经验分布函数计算

随机截尾数据下，经验分布函数的计算有两种方法，分别为残存比率法和平均秩次法[6-7]。

2.1.1残存比率法

残存比率法为通用公式，在无删除样品时同样适用。残存比率法是由概率乘法公式得到的，因此它适用于样本量较大的情况。

产品在某时刻ti的可靠度为：

R(ti)=R(ti-1)·S(ti)

(2)

(3)

式中：ξ是指产品从处于完好状态开始直到进入失效状态所经历的时间，也可称之为寿命，是一非负随机变量。

根据样本观测值进行估计，其计算公式为：

(4)

(5)

根据式(2)，经验分布函数的计算公式为：

(6)

2.1.2平均秩次法

平均秩次法是一种在随机截尾数据下经验分布函数的较精确的计算方法，其思想为：对于一组随机截尾的样本数据，可按其失效时间和删失时间的大小排列成一组顺序统计量，其中每一个样品的失效时间都有一个顺序号，此顺序称为秩次。而对于那些尚未失效而中途撤离的样品，什么时间失效无法预计，然而可以估计出它们所有可能的秩次，再求出平均秩次，将平均秩次代入近似中位秩公式，即可求出其经验分布函数。

对于随机截尾数据，统计学家们给出一个计算平均秩次的增量公式，为：

(7)

(8)

式中：Ak为失效样品的平均秩次，下标k代表失效样品的顺序号；Ak-1为前一个失效样品的平均秩次；i为所有产品的排列顺序号，按故障时间和删除时间的大小排列。

然后将平均秩次代入近似中位秩公式计算样本的经验分布函数，为：

(9)

2.2随机截尾数据下的两参数威布尔分布的最小

二乘估计法

对于随机截尾数据，假设失效样品的数量为n1，删除样品的数量为n2，则n1+n2=n。假设失效样品的失效时间的顺序统计量为t1≤t2≤…≤tn1，根据残存比率法或平均秩次法可计算其经验分布函数为Fn(tk)(k=1,2,…,n1)。

式(1)可以表示为线性方程形式，为：

(10)

因此可以根据最小二乘法来估计随机截尾数据下的两参数威布尔分布。

令

(11)

需拟合的回归直线方程为：

y=a+bx

(12)

根据最小二乘法原理，回归系数和相关系数为：

(13)

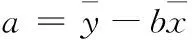
(14)

(15)

式中：

2.3两参数威布尔分布参数的求解

根据回归系数a、b，威布尔分布的参数为：

(16)

2.4线性相关程度检查

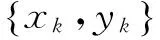
3随机截尾数据下的液压泵的两参数威布尔

分布建模流程

基于两参数威布尔分布的随机截尾数据下的液压泵可靠性数据分析的一般流程如图1所示。

图1　基于两参数威布尔分布的随机截尾数据下

首先收集液压泵的随机截尾型可靠性数据，然后根据残存比率法或平均秩次法计算样本的经验分布函数。假设服从两参数威布尔分布，根据数理统计的基本原理，对液压泵的可靠性数据进行参数估计，并使用假设检验方法来验证寿命分布类型，最后再进行液压泵可靠性参数的计算。

4　液压泵的可靠性分析仿真试验

4.1仿真数据

4.2经验分布函数的计算

采用残存比率法计算失效样品的残存概率S(ti)及经验分布函数Fn(ti)的计算结果如表1所示；采用平均秩次法计算失效样品的平均秩次Ak及经验分布函数Fn(ti)的计算结果如表1所示。

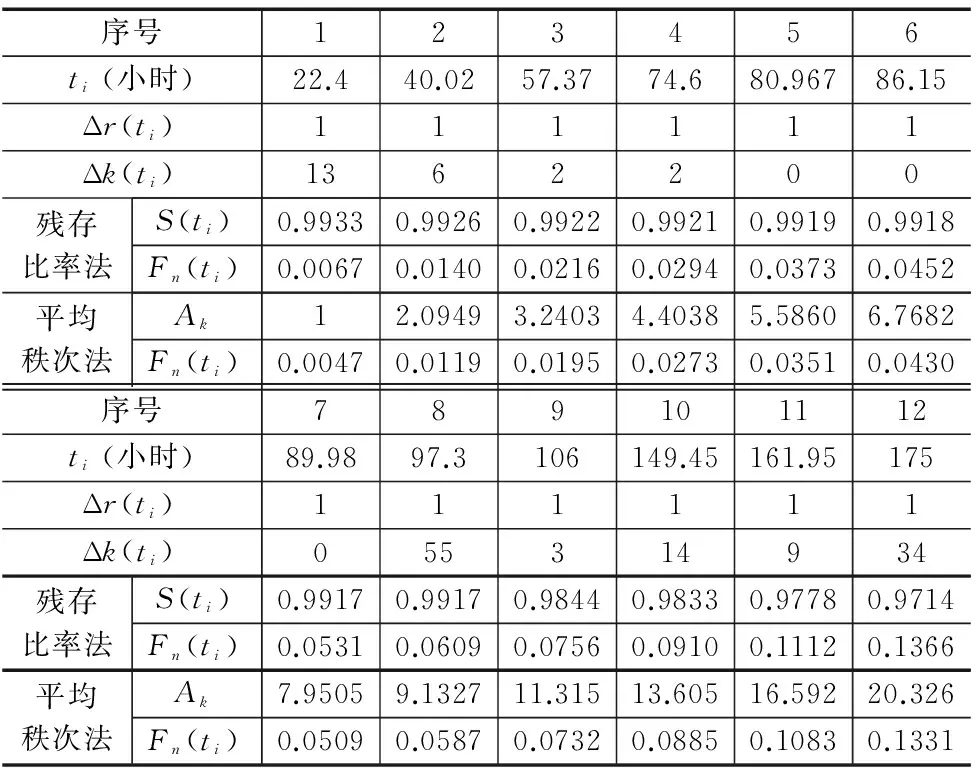
表1　液压泵的外场使用故障数据及平均秩次、

4.3两参数威布尔分布模型的建立

(1)基于残存比率法的两参数威布尔分布模型

在残存比率法计算经验分布函数的基础上，两参数威布尔分布的参数估计(最小二乘法)结果为：尺度参数η1=650.43，形状参数m1=1.52，相关系数rxy1=0.98998。当显著水平为0.01时，相关系数临界值为rα=0.6614，由于rxy1>rα时，则认为回归效果显著。

(2)基于平均秩次法的两参数威布尔分布模型

在平均秩次法计算经验分布函数的基础上，两参数威布尔分布的参数估计(最小二乘法)结果为：尺度参数η2=571.61，形状参数m2=1.6651，相关系数rxy2=0.99207。当显著水平为0.01时，由于rxy2>rα时，则认为回归效果显著。

(3)小结

由于rxy 1< rxy 2，因此基于平均秩次法的液压泵两参数威布尔分布模型比基于残存比率法的两参数威布尔分布模型更为精确。因此对于随机截尾数据，平均秩次法比残存比率法的建模效果更好。

基于平均秩次法的两参数威布尔分布模型的概率图如图2所示。从图2可以看出，数据点大体上是沿一条直线分布的，这直观地说明了该型液压泵的首次失效时间可以用两参数威布尔分布来建模。

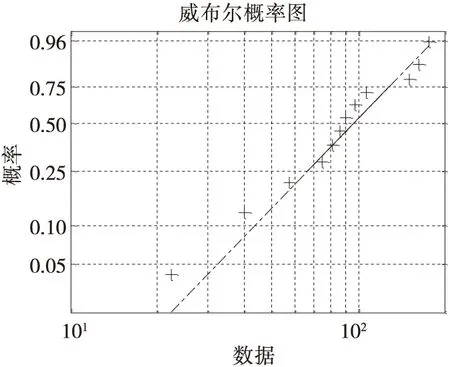
图2　两参数威布尔分布的概率图

4.4基于平均秩次法的液压泵可靠性参数的计算

液压泵首次失效时间的基于平均秩次法的两参数威布尔分布的分布函数为：

分布密度函数为：

失效率函数为：

失效率曲线如图3所示，可以看出，失效率随时间增长呈增长特性，因此液压泵的失效类型为耗损失效，故障原因主要是由于老化、疲劳和耗损引起的。因此通过可靠性定量分析，就可以采取预防维修或更新措施，更换某些元器件，把液压泵上升的失效率降下来。

图3　液压泵的失效率曲线

可靠度函数为：

平均寿命为：

θ=ηΓ(1+1/m)=510.78(h)

5　结论

由于两参数威布尔分布拟合能力强、适用范围广，是可靠性工程中常用的分布之一，对其进行精确的参数估计在可靠性分析中有相当重要的意义。

本文首先提出了一种基于随机截尾数据的两参数威布尔分布的建模方法，并将其应用于某型液压泵的可靠性数据分析，最后进行了仿真试验研究。仿真试验结果表明：①平均秩次法原理清晰，计算过程方便快捷，同时还具有计算机编程方便、拟合精度高等优点，基于平均秩次法的液压泵两参数威布尔分布模型比基于残存比率法的两参数威布尔分布模型更为精确；②两参数威布尔分布拟合能力强，验证了威布尔分布的优越性。研究成果为基于随机截尾数据的液压泵提供了一种更为精确的可靠性分析方法。

[1] 胡良谋，曹克强，任博，等. 飞机液压系统使用故障统计分析[M]. 北京：国防工业出版社，2014.

[2] 王占林. 飞机高压液压能源系统[M]. 北京：北京航空航天大学出版社，2004.

[3] 梁广辉，薛俊杰，胡良谋，等. 基于非对称贴近度的飞机液压系统使用工况模糊综合评判[J]. 组合机床与自动化加工技术，2014(4)：83-86.

[4] Weibull W. A statistical distribution function of wide applicability[J]. Journal of Applied Mechanics, 1951, 18 (3): 293-297.

[5] 凌丹. 威布尔分布模型及其在机械可靠性中的应用研究[D].成都：电子科技大学，2010.

[6] 贺国芳. 可靠性数据的收集与分析[M]. 北京：国防工业出版社，1995.

[7] 赵宇，杨军，马小兵. 可靠性数据分析教程[M]. 北京：北京航空航天大学出版社，2009.

[8] 范晋伟，梁晓霞，郑德荣，等. 基于灰关联度的数控磨床故障间隔时间分布模型决策[J]. 组合机床与自动化加工技术，2014(8)：78-81.

[9] 孟庆东，杨珍.基于MCMC的MTBF值区间估计方法研究[J]. 组合机床与自动化加工技术，2013(2)：67-69.

[10] 董慧敏，刘勇军，张新锋. 镁锭切削机故障分布拟合与MTBF评估研究[J]. 组合机床与自动化加工技术，2014(1)：107-113.

(编辑赵蓉)

Two Parameter Weibull Distribution Model of Fault Distribution for Hydraulic Pump Based on Random Censored Data

XIONG Shen-hui1, HU Liang-mou2, HU Fei3, CAO Ke-qiang2, JING Tao2, GAO Bin2

(1. Command Ministry of Air Force Logistics Ministry, Beijing 100720, China;2. College of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi′an 710038，China)

Operational reliability of hydraulic pump can factually reflect the actual reliability level and weak part. The operational reliability data of hydraulic pump has characteristic of random censored, therefore its operational reliability analysis is very difficult. A modeling method of two parameter Weibull distribution based on random censored data is presented. And then the method is used to establish the two parameter Weibull distribution model of one hydraulic pump. The simulation test is carried out finally. The simulation test results show that the two parameter Weibull distribution model of hydraulic pump based on the mean rank order method is more accurate than the two parameter Weibull distribution model based on the survival ratio method. And the simulation test results show that the Weibull distribution is good. The research work can provide a more accurate method of reliability analysis for hydraulic pump based on random censored data.

hydraulic pump; random censored data; two parameter weibull distribution; mean rank order method; survival ratio method

1001-2265(2016)04-0109-04DOI:10.13462/j.cnki.mmtamt.2016.04.029

2015-06-02；

2015-07-07

中国博士后科学基金特别资助项目(201003788)

熊申辉(1977—)，男，安徽桐城人，空军后勤部工程师，硕士，研究方向为飞机系统可靠性，(E-mail)xiongsh_2015@163.com。

TH137;TG506

A