A simple method for estimating bed shear stress in smooth and vegetated compound channels*

Yu-qi SHAN （单钰淇）， Chao LIU （刘超）， Mao-kang LUO （罗懋康）， Ke-jun YANG （杨克君）

1. College of Mathematics， Sichuan University， Chengdu 610065， China， E-mail: yuqi_shan@qq.com

2. State Key Laboratory of Hydraulics and Mountain River Engineering and College of Water Resource and Hydropower， Sichuan University， Chengdu 610065， China



A simple method for estimating bed shear stress in smooth and vegetated compound channels*

Yu-qi SHAN （单钰淇）1， Chao LIU （刘超）2， Mao-kang LUO （罗懋康）1， Ke-jun YANG （杨克君）2

1. College of Mathematics， Sichuan University， Chengdu 610065， China， E-mail: yuqi_shan@qq.com

2. State Key Laboratory of Hydraulics and Mountain River Engineering and College of Water Resource and Hydropower， Sichuan University， Chengdu 610065， China

Instead of a large number of measurements of the streamwise velocity， a simple method is proposed to estimate the bed shear stress in smooth and vegetated compound channels， based on the Darcy-Weisbach equation. This method contains a dimensionless parameter， to represent the relationship between the bed shear stress and the velocity close to the channel bed， which is determined in each divided domain. This method is verified in two smooth compound channels with different geometries， and in one compound channel with emergent floodplain vegetation. The comparison of predicted and measured bed shear stresses indicates the good predictive capability of this method， particularly in the mixing region. This method is further discussed for a channel with submerged vegetation. Once the values ofin the main channel and the floodplain are determined， this method is a practical tool for estimating the bed shear stress based on a small number of measurements ofin compound channels.

predictive method， bed shear stress， compound channel， vegetation

Introduction

In natural rivers， the bed shear stress is important in determining the local bed erosion， the sediment bedload and the particle resuspension. The sediment deposition enhances the potential of the macrophyte expansion， to reinforce the development of river banks，vegetated islands and floodplains. This is an efficient way to stabilize the channel bed and protect the river bank. The flow often inundates floodplains during the flood period， and thus a compound channel emerges，whose flow characteristics （e.g. the vertical profile of velocity， and the secondary flow） were extensively investigated［1，2］. The geometry of the compound channel can be discretized into several linear elements and the most common type is the trapezoidal compound channel （see Fig.1（a））. Compared to the mainchannel， the floodplains with low velocities provide a more suitable environment for the sediment deposition and the growth of macrophyte. Thus a compound channel with vegetation floodplains is formed， as shown in Fig.1（b）. Particularly， the significant enhancement of the shear stress can be observed in the mixing region （wider than Region 2 in Fig.1） due to the velocity difference between the main channel and floodplain flows［3］. Moreover， a complicated lateral distribution of the bed shear stress can be observed in that region， which is difficult to be accurately predicted.

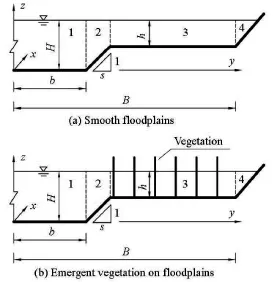
Fig.1 Cross-sections of compound channels. Regions 1， 2， 3 and 4 represent the main channel， the main channel side slope region， the floodplain， and the floodplain side slope region， respectively

Table 1 Experimental parameters in compound channels

Three-dimensional velocities measured by the acoustic Doppler velocimeter （ADV） were related to the bed shear stress［4］. To determine the bed shear stress， a relation between the turbulent kinetic energy（TKE） and the Reynolds shear stresswas proposed with a dimensionless parameter to be separately calibrated in laboratory experiments［5］and natural rivers［6］. However， those methods can only provide accurate predictions of the bed shear stress in single channels. In compound channels， some analytical and numerical methods might be used in predicting the lateral distribution of the bed shear stress［3，7-12］， but the common disadvantage of these models is the fact that one has to determine the effect of secondary flows（specifically， the secondary flow parameter in these models）. To calibrate the secondary flow parameter，detailed measurements of three-dimensional velocities at a transection of a compound channel are needed［8，9］.

The Darcy-Weisbach equation may be used to predict the bed shear stressas

To obtain the accurate lateral distribution ofa large number of measurements forhave to be made， whereis the time-average velocity. The inaccurate measurement formay directly result in a poor prediction ofdue to the relationUntil now laboratory experiments are the most efficient approach to obtain sufficient data at large temporal and spatial scales under a specific flow condition， but it is difficult to make a large number of measurements due to limited resources. In field measurements （particularly in rapidly flowing large rivers）， it is most difficult to ensure the accuracy with a reasonable expense. Therefore， in the current research we propose a simple method to estimate the bed shear stress with a small number of measurements of velocity.

1. Data from published literature

All experimental data in this paper are obtained from the flood channel facility （FCF） in the UK. Different channel geometries and floodplain conditions are considered （see Table 1）. The details of the data acquisition system were described in Knight and Sellin［13］， Knight and Shiono［14］and Rameshwaran and Shiono［3］， and a brief description is as follows.

The UK-FCF consisted of a 56 m long and 10 m wide experimental flume with a maximal discharge capacity of 1.1 m3/s. Six groups of experiments were conducted in a straight compound channel with smooth floodplains （FCF 01， 02， 03， 08 and 10） and vegetated floodplains （FCF 07）. In all cases， the width of the main channelwas the same， but the floodplain condition and the main channel side slopewere different （see details in Table 1）. The measurement section was at a position 36 m downstream from the inlet of the flume. Velocity was measured by a two-dimensional LDA system， and the bed shear stress was measured by the Preston tube. The bed slopewas 0.001027， and the bank heightwas 0.15 m. The surface of those compound channels was smooth， and the Manning coefficient was 0.0099 in smooth channels. The floodplain vegetation was modeled by rigid wooden rods， which were placed vertically on smooth floodplains. The vegetation diameter was 0.025 m and the vegetation density was 12 rods/m2. Cross-sections of both smooth and vegetated compound channels are shown in Fig.1. Regions 1， 2， 3 and 4represent the main channel， the main channel side slope region， the floodplain， and the floodplain side slope region， respectively.

Fig.2 Vertical profile of streamwise velocity on the centerline of main channel， based on the experimental data from FCF02andrepresent the velocity atand， respectively

Fig.3 Sketch for vertical profile of streamwise velocity on the centerline of main channel. The dashed line is the crosssection of compound channel

2. Method for estimating bed shear stress

The velocity at the channel bed surface is considered to be zero for the non-slip boundary. In the near bed region （also called the “inner region”）， the velocity increases rapidly， with a linear relationship between the mixing lengthand the flow depth. In the outer region， if this assumption is still valid， the traditional logarithmic vertical profile of velocity can be obtained. However， the velocity dip-phenomenon observed near the free water surface cannot be described in that velocity profile. The dip-phenomenon of velocity， which is attributed to the secondary flow， is distinct in compound channels［15］. Figure 2 shows the vertical distribution of the streamwise velocity in compound channels under different flow conditions，based on the experimental data from FCF02. Here FCF020701 is taken as an example to introduce the vertical profile of streamwise velocity. The velocityclose to the channel bedis not equal to zero. A stable increase of velocity is observed from， with the occurrence of maximal velocityat. Then， the streamwise velocity decreases with the increase ofz， and the surface velocity， which is smaller than， is observed at. A sketch of the vertical profile of the streamwise velocity on the centerline of the main channel is shown in Fig.3.

For the lateral distribution of the depth-averaged velocity， the detailed measurement for the streamwise velocity is needed in both lateral and vertical directions. Instead of the large number of measurements， we propose only to measure the lateral distribution of the bed velocity. A dimensionless parameteris proposed to show the relationship betweenandas follows

Combing Eqs.（1） and （2）， the bed shear stress may be estimated by

Fig.4 Lateral distributions ofat different flow depths， based on the experimental data from FCF02. The first lateral distribution ofis FCF020201. Each distribution ofis shifted upward by 0.02 from the previous one. Solid lines represent，andin the main channel，the mixing region and the floodplain， respectively. Dashed line indicates the channel bed.indicates the width of the mixing region

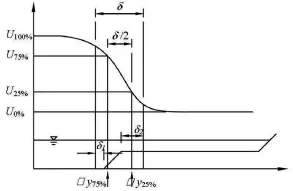
Fig.5 Sketch of velocities and their corresponding positions in a compound channel， based on Fig.3 in Van Prooijen et al.［16］.andare located atand， respectively

Based on the experimental data in Table 1， the value ofat every position across the channel is calculated from Eq.（2）. Then，is laterally integrated fromtoin the main channel， and fromtoon the floodplain， where（as denoted in Fig.5）. Thus， the mean value ofis obtained in the main channel and the floodplain as follows:

Using the experimental data from FCF02， 08 and 10， the values ofandare plotted against the relative flow depthin Fig.6. In the main channel，is a constant， equal to 1.43. However， on the floodplainincreases linearly with， that may be expressed as

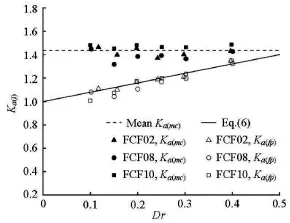
Fig.6 Relationship betweenand relative flow depth. The dashed line represents the mean value of. The side slope of solid line which isin Eq.（6） is equal to 0.8

Table 2 The mean value of absolute relative errorin two compound channels with smooth floodplains （FCF01 and 03）and in one compound channel with vegetated floodplains （FCF07）

Table 2 The mean value of absolute relative errorin two compound channels with smooth floodplains （FCF01 and 03）and in one compound channel with vegetated floodplains （FCF07）

FCF01 　FCF03 　FCF07 % Dr Dr /Φ / Φ % Dr /Φ% 0.092 　5.8 　0.098 　6.8 　0.094 　23.4 0.146 　4.6 　0.153 　6.5 　0.150 　13.0 0.196 　5.1 　0.201 　4.6 　0.193 　6.4 0.246 　9.4 　0.243 　4.2 　0.248 　6.1 0.299 　1.1 　0.301 　6.4 　0.315 　10.0 0.400 　4.8 　0.395 　2.8 　0.400 　10.1 Average （standard deviation） 　5.1 （2.7） 　Average （standard deviation） 　5.2 （1.7） 　Average （standard deviation） 　11.5 （6.4）

However， the determination ofis not straightforward due to the strong shear velocity （i.e.， high） in the mixing region. Van Prooijen et al.［16］proposed a method to predict the width of the mixing regionin a compound channel as follows

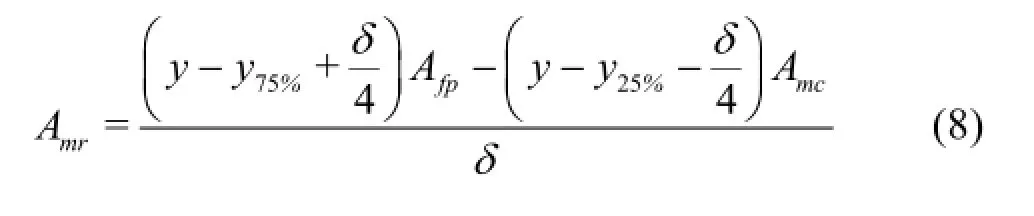
Finally， the bed shear stress in the mixing region may be estimated using Eq.（3）.

3. Applications and discussions

To show the difference between the measured and estimated bed shear stresses， the absolute relative erroris defined as

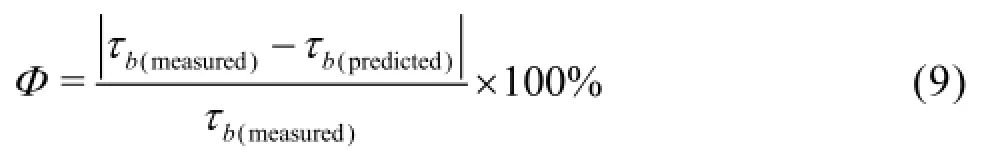
The mean value of is defined as follows

First， this predictive method for the bed shear stress is verified in the cases of two smooth compound channels （FCF01 and 03）. Those two channels differ in the width of the floodplains （specifically， 4.1 m inFCF01 and 0.75 m in FCF03）. The value ofin each run for FCF01 and 03 is shown in Table 2. The largestvalue is 9.4% and the smallest one is only 1.1%. In both cases， thevalue in most runs is about 5%， which is consistent with the mean value ofin all six runs. The predictive error of this method comes from two sources: （1） In this model，the friction factor is considered to be a constant in each divided region （i.e.， Regions 1 to 4 in Fig.1）. Thus， the difference between the measured and predicted friction factors may be due to this kind of error（for the smooth channel: see Fig.13 in Shiono and Knight［9］， for the vegetated channel: see Fig.6 in Rameshwaran and Shiono［3］）. However， for the convenience of calculation， the friction factor has to be assumed to be a constant in each divided domain as in Refs.［3，7，8，17-20］， （2） The difference between the predicted and measuredmay be due to other kinds of error （i.e.， the difference between the line and dots in Fig.6）. In addition， the measurement error formay also result in errors， which are ignored by considering the measurement errors forsmall errorindicates the good predictive capa-. Such a bility of this method for the bed shear stress in smooth compound channels. Shiono and Knight［9］proposed a two-dimensional model for predicting. However， the prediction ofwas not good for the mixing region where the constant friction factor was assumed. Yang et al.［21］proposed a model to predictin compound channels by borrowing the concept of the energy transportation through a minimum relative distance towards the nearest boundary from the single channel， but poor predictions ofwere seen in the mixing region. This may be due to the fact that the strong momentum exchange occurs in the mixing region， which is not considered in that model［21］. Both studies［9，21］indicate that it is difficult to accurately predict the bed shear stress in the mixing region. To further discuss the predictive capability of this method， the lateral distributions of predicted and measuredare shown in Fig.7 at two flow depths （a low flow，， and a high flow，）. The predictedclosely follows the measured one， though small differences occur at some positions. More importantly， the predictions ofin the mixing region are accurate， indicating that the determination ofin Eq.（8） makes sense. In addition， different widths of floodplains in two channels （FCF01 and 03） should be noted. Though we use the values ofthat were determined in three different channels （FCF02， 08 and 10）， good predictions of the bed shear stress are obtained in FCF01 and 03. This indicates that thevalue may be independent of the floodplain geometry. However， the geometry of the main channel in this study remains almost the same， so the effect of the geometry on the value ofcannot be seen.

Fig.7 Comparison of measured and predicted bed shear stresses in smooth compound channels

In the channel with emergent vegetation， the velocity remains to be a constant in the vertical direction［22］. However， the velocity profile varies significantly under the flow condition of submerged vegetation. That profile may be divided into three regions（specifically， the above canopy， the below canopy and the inner region）［23］. Based on the studies of vertical velocity distributions in vegetated channels［23，24］， a sketch of vertical profiles of the streamwise velocity for emergent and submerged vegetations is shown in Fig.8. Note that both pictures in Fig.8 are not in the real scale. For the flow with submerged vegetation，Huthoff et al.［25］proposed a relationship （Eq.（11））between the depth-averaged velocityand the mean velocity in the resistance layer， where the resistance layer is the region below the submerged canopy （see Fig.1 in Huthoff et al.［25］）.

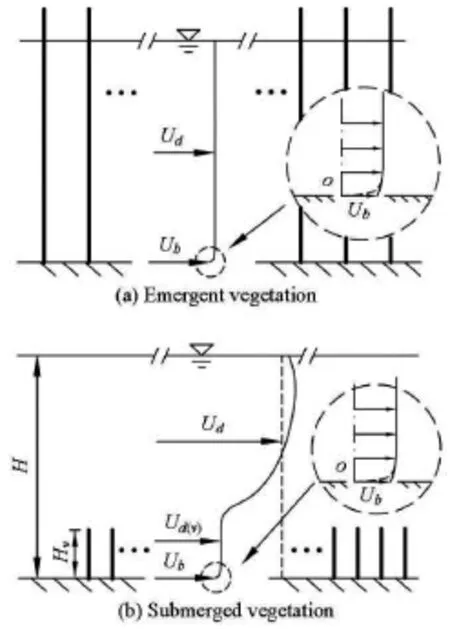
Fig.8 Sketch of vertical profile of streamwise velocities. Black bars indicate vegetation and both pictures are not in the real scale

Combining Eqs.（2） and （11）， Eq.（3） may be rewritten as follows

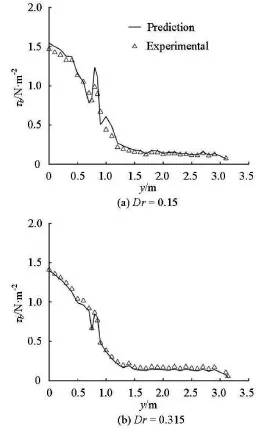
Fig.9 Comparison of measured and predicted bed shear stress in compound channels with emergent floodplain vegetation， based on the experimental data from FCF07

The experimental data from FCF07 is used to verify the proposed method in compound channels with emergent floodplain vegetation. Thevalue in all six runs of FCF07 is shown in Table 2. Compared to the small errors in smooth compound channels（FCF01 and 03）， the increase of errors in vegetated channels （FCF07） has to be noted， particularly in the run with. Generally， the values ofin the vegetated compound channel are twice as large as those in smooth channels. Consistent with this fact， the mean value ofin FCF07is also twice larger than those in FCF01 and 03 （=5.1% and 5.2%， respectively）. This is because under such a high flow condition of floodplains （） the occurrence of vortex street behind individual rigid rods and the presence of horseshoe vortex at the leading edge of each rod may affect the measurement of the bed shear stress. Also， there is not a distinct trend forvalue at different. The standard deviation of（2.7% in FCF01， 1.7% in FCF03 and 6.4% in FCF07， see Table 1） indicates that it is more difficult to accurately predict the bed shear stress in vegetated channels than in smooth channels. For vegetated compound channels， Rameshwaran and Shiono［3］proposed a model to predict the lateral distribution of， but the predictions were not good in the mixing region. Then， Liu et al.［7］managed to accurately model the lateral distribution of the bed shear stress， particularly in the mixing region. However， these two models have the disadvantage that the secondary flow parameter has to be calibrated before predicting. To show the performance of the proposed method in a vegetated compound channel， the lateral distributions of measured and predicted bed shear stresses atand 0.3 are shown in Fig.9. The comparison of predicted and measured bed shear stresses indicates that thismethod is capable of estimating the bed shear stress in the compound channel with emergent floodplain vegetation， particularly， in the mixing region.

However， the vertical velocity distribution in regions of submerged vegetation， as shown in Fig.8（b），is more complicated than that in regions of emergent vegetation［1］. In Fig.8（b）， the velocity above the canopy gradually increases following the logarithmic pattern， with. We can still use Eq.（12） to predict the bed shear stress， butmay vary with the flow depth instead of being a constant. Apparently， the determination ofis necessary before applying Eq.（12） to predict. An extensive review of previous literature does not reveal available data （bothand） in compound channels with submerged vegetation. Thus， the further validation of the proposed method cannot be done. Nevertheless， the predictive capability of this method in compound channels with smooth floodplains and with emergent floodplain vegetation is impressive.

4. Conclusion

Based on the experimental data from UK-FCF，the vertical profile of the streamwise velocity is analyzed. At the position very close to the channel bed， the velocity is not equal to zero （Figs.2 and 3）. A dimensionless parameter（Eq.（2）） is proposed to show the relationship between the depth-averaged velocity and the bed velocity. The value ofis a constant in the main channel， but it linearly varies with the relative flow depth on the floodplain.（see Eq.（3）） is determined in the main channel， the mixing region and the floodplain， respectively. The width of the mixing region is larger than the width of the main channel side slope （see Fig.5）， and it is determined by the concept of van Prooijen et al.［16］（see Eq.（8））. Once the parameteris determined in a new compound channel， this method is a very practical tool for estimating the bed shear stress in that channel. The proposed method is verified in two smooth compound channels with different geometries of floodplains and in one vegetated compound channel with emergent vegetation. The predictive capability of this method for the bed shear stress in both smooth and vegetated channels is good， particularly， in the mixing region.

References

［1］ YANG K.， CAO S. and KNIGHT D. W. Flow patterns in compound channels with vegetated floodplains［J］. Journal of Hydraulic Engineering， ASCE， 2007， 133（2）: 148-159.

［2］ LIU Chao， SHAN Yu-qi and YANG Ke-jun et al. The characteristics of secondary flows in compound channels with vegetated floodplains［J］. Journal of Hydrodynamics， 2013， 25（3）: 422-429.

［3］ RAMESHWARAN P.， SHIONO K. Quasi two-dimensional model for straight overbank flows through emergent［J］. Journal of Hydraulic Research， 2007， 45（3）: 302-315.

［4］ KIM S. C.， FRIEDRICHS C. T. and MAA J.-Y. et al. Estimating bottom stress in tidal boundary layer from acoustic Doppler velocimeter data［J］. Journal of Hydraulic Engineering， ASCE， 2000， 126（6）: 399-406.

［5］ HOPKINSON L.， WYNN-THOMPSON T. Streambank shear stress estimates using turbulent kinetic energy［J］. Journal of Hydraulic Research， 2012， 50（3）: 320-323.

［6］ POPE N. D.， WIDDOWS J. and BRINSLEY M. D. Estimation of bed shear stress using the turbulent kinetic energy approach-A comparison of annular flume and field data［J］. Continental Shelf Research， 2006， 26（8）: 959-970.

［7］ LIU C.， LUO X. and LIU X. et al. Modeling depth-averaged velocity and bed shear stress in compound channels with emergent and submerged vegetation［J］. Advances in Water Resources， 2013， 60: 148-159.

［8］ LIU C.， WRIGHT N. and LIU X. et al. An analytical model for lateral depth-averaged velocity distributions along a meander in curved compound channels［J］. Advances in Water Resources， 2014， 74: 26-43.

［9］ SHIONO K.， KNIGHT D. W. Turbulent open-channel flows with variable depth across the channel［J］. Journal of Fluid Mechanics， 1991， 222: 617-646.

［10］ YANG K.， NIE R. and LIU X. et al. Modeling depthaveraged velocity and boundary shear stress in rectangular compound channels with secondary flows［J］. Journal of Hydraulic Engineering， ASCE， 2012， 139（1）: 76-83.

［11］ HUAI Wen-xin， XU Zhi-gang and YANG Zhong-hua et al. Two dimensional analytical solution for a partially vegetated compound channel flow［J］. Applied Mathematics and Mechanics （English Edition）， 2008， 29（8）: 1077-1084.

［12］ JING H.， GUO Y. and LI C. et al. Three-dimensional numerical simulation of compound meandering open channel flow by the Reynolds stress modelJ］. International Journal for Numerical Methods in Fluids， 2009，59（8）: 927-943.

［13］ KNIGHT D. W.， SELLIN R. H. J. The SERC flood channel facility［J］. Water and Environment Journal，1987， 1（2）: 198-204.

［14］ KNIGHT D. W.， SHIONO K. Turbulence measurements in a shear layer region of a compound channel［J］. Journal of Hydraulic Research， 1990， 28（2）: 175-196.

［15］ CARLING P. A.， CAO Z. and HOLLAND M. J. et al. Turbulent flow across a natural compound channel［J］. Water Resources Research， 2002， 38（12）: 6-1-6-11.

［16］ Van PROOIJEN B. C.， BATTJES J. A. and UIJTTEWAAL W. S. J. Momentum exchange in straight uniform compound channel flow［J］. Journal of Hydraulic Engineering， ASCE， 2005， 131（3）: 175-183.

［17］ LIU C.， SHAN Y. and LIU X. et al. Method for assessing stage-discharge in meandering compound channels［J］. Proceedings of ICE-Water Management， 2016， 169（1）: 17-29.

［18］ LIU Chao， LIU Xing-nian and YANG Ke-jun. Predictive model for stage-discharge curve in compound channels with vegetated floodplains［J］. Applied Mathematics and Mechanics （English Edition）， 2014， 35（12）: 1495-1508.

［19］ SHAN Yu-qi， LIU Chao and LUO Mao-kang. Simple analytical model for depth-averaged velocity in meandering compound channels［J］. Applied Mathematics and Mechanics （English Edition）， 2015， 36（6）: 707-718.

［20］ LIAO H.， KNIGHT D. W. Analytic stage-discharge formulae for flow in straight trapezoidal open channels［J］. Advances in Water Resources， 2007， 30（11）: 2283-2295.

［21］ YANG S.， YU J. and WANG Y. Estimation of diffusion coefficients， lateral shear stress， and velocity in open channels with complex geometry［J］. Water Resources Research， 2004， 40（5）: W05202.

［22］ WANG Wen， HUAI Wen-xin and GAO Meng. Numerical investigation of flow through vegetated multi-stage compound channel［J］. Journal of Hydrodynamics， 2014，26（3）: 467-473.

［23］ HUAI W.， ZENG Y. and XU Z. et al. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation［J］. Advances in Water Resources， 2009， 32（4）: 487-492.

［24］ LIU C.， NEPF H. Sediment deposition within and around a finite patch of model vegetation over a range of channel velocity［J］. Water Resources Research， 2016， 52（1）: 600-612.

［25］ HUTHOFF F.， AUGUSTIJN D. and HULSCHER S. J. M. H. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation［J］. Water Resources Research， 2007， 43（6）: W06413.

July 6， 2015， Revised October 12， 2015）

* Project supported by the National Natural Science Foundation of China （Grant Nos. 11171238， 51539007 and 51479128）.

Biography: Yu-qi SHAN （1988-）， Female， Ph. D. Candidate

Correspondind author: Ke-jun YANG，

E-mail: yangkejun@163.com