A robust WENO scheme for nonlinear waves in a moving reference frame*

Stavros KONTOS， Harry B. BINGHAM， Ole LINDBERG， Allan P. ENGSIG-KARUP

1. Department of Mechanical Engineering， Technical University of Denmark， Denmark，

E-mail: stakon@mek.dtu.dk

2. Department of Applied Mathematics and Computer Science， Technical University of Denmark， Denmark



A robust WENO scheme for nonlinear waves in a moving reference frame*

Stavros KONTOS1， Harry B. BINGHAM1， Ole LINDBERG1， Allan P. ENGSIG-KARUP2

1. Department of Mechanical Engineering， Technical University of Denmark， Denmark，

E-mail: stakon@mek.dtu.dk

2. Department of Applied Mathematics and Computer Science， Technical University of Denmark， Denmark

For robust nonlinear wave simulation in a moving reference frame， we recast the free surface problem in Hamilton-Jacobi form and propose a Weighted Essentially Non-Oscillatory （WENO） scheme to automatically handle the upwinding of the convective term. A new automatic procedure for deriving the linear WENO weights based on a Taylor series expansion is introduced. A simplified smoothness indicator is proposed and is shown to perform well. The scheme is combined with high-order explicit Runge-Kutta time integration and a dissipative Lax-Friedrichs-type flux to solve for nonlinear wave propagation in a moving frame of reference. The WENO scheme is robust and less dissipative than the equivalent order upwind-biased finite difference scheme for all ratios of frame of reference to wave propagation speed tested. This provides the basis for solving general nonlinear wave-structure interaction problems at forward speed.

nonlinear waves， Weighted Essentially Non-Oscillatory （WENO）， finite difference

Introduction

Exploiting the advantages of the high-order finite difference method in solving nonlinear potential flow，wave-structure interaction problems for ships travelling with steady forward speed， requires robust numerical methods. The proposed method extends previous works by Engsig-Karup et al.［1，2］， Lindberg et al.［3］and Afshar et al.［4］on developing robust strategies for efficient modeling of nonlinear waves and linear and nonlinear wave-structure interaction. When the linearized problem is considered， a one-point upwind-biased approximation of the convective derivatives in the free surface boundary conditions is sufficient to ensure stability［5］. For nonlinear problems however， this is not found to be robust for all combinations of ship speed and wave celerity. In this paper， a simplified version of the Weighted Essentially Non-Oscillatory（WENO）［6］finite difference scheme is proposed for stabilizing the solution of the fully nonlinear problem. This scheme is tested using the nonlinear wave propagation problem in a moving frame of reference which mimics a forward speed seakeeping problem. The results of these strenuous numerical experiments indicate that it is robust and accurate.

1. A simplified WENO finite difference scheme for the convective terms

The scheme is presented in one dimension， but for 3-D problems it is applied in the same way to both of the horizontal convective terms. The WENO scheme creates two approximations of the convective derivativeusing a left and a right biased stencil as shown in Fig.1.

These two approximations are combined with an appropriate flux to give the final result. Each of these stencils consists ofsub-stencils. On a left biased stencil， WENO 3computes three third order approximationstobased on each of thesub-stencils. These approximations are combined using non-linear weightsto compute the final result

Fig.1 WENO 3 left and right biased stencils

Following Yamaleev and Carpenter［7］the nonlinear weights are defined as:

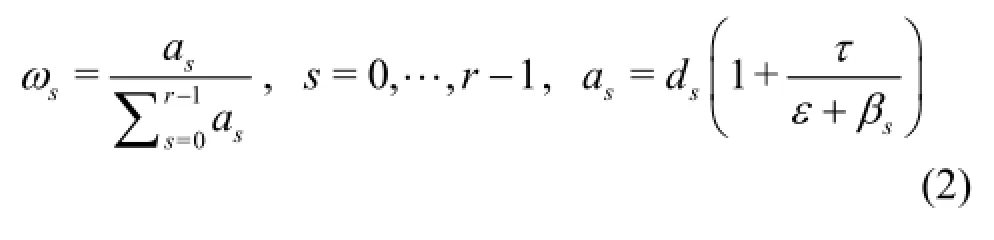
This is a sum of all possible higher derivatives on the stencil， scaled to have units of velocity （m/s） and is thus a measure of the smoothness of the velocity. It becomes large whenever a discontinuity exists in the solution and thus forces the associated weight to become small for that stencil. The factorin Eq.（2） is defined as the squared normalized highest order derivative on the full stencil ofpoints，

This expression for the nonlinear WENO weights（Eq.（2）） is chosen instead of the classical weights by Liu et al.［6］because it is found to introduce less numerical dissipation into the nonlinear wave solution. Forclarification， thecoefficients can be expressed as in Borges et al.［10］

where

Therefore， the relative importance of stencilis larger and the scheme is less dissipative. More detailed analysis can be found in Borges et al.［10］. We note that as the linear weights are derived on a uniform grid， non-uniform spacing is introduced via a transformation between the physical grid and a unit-spaced reference grid.

Test the Performance of the New Smoothness Indicator

The convergence of the simplified smoothness indicator is compared with the tabulated values from the literature for evaluating the derivative of a smooth and a discontinuous function. The smooth test function is given by

And the discontinuous test function is:

where the offset is introduced to avoid any fortuitous cancellation of errors. No flux is used to combine the left and right biased approximations. On the left of the discontinuity the left biased stencil is used and on the right of the discontinuity the right biased stencil is used，which simulates the use of an exact Riemann solver. In the case of the smooth function there is no difference in the choice of right or left stencil. The relative error in each case is defined by

The convergence of the two approximations for the smooth function is shown in Figs.1-4 and we can see that the two smoothness indicators give nearly identical results and converge at the expected order of accuracy in all cases. We note that the accumulation of round-off errors prevents the relative error from dropping below approximately 10¯13as can be seen by the levelling of the high-order errors on refined grids. The results for the discontinuous function are shown in Figs.5-9 and again the two methods give nearly identical results， providing the expected rate of convergence in all cases. These results support the conclusion that the proposed smoothness indicator is able to function as well as the tabulated values in controlling the WENO scheme.

Fig.2 WENO 3 convergence

Fig.3 WENO 4 convergence

Fig.4 WENO 5 convergence

Fig.5 WENO 6 convergence

Fig.6 WENO 3 convergence

Fig.7 WENO 4 convergence

Fig.8 WENO 5 convergence

Fig.9 WENO 6 convergence

2. Application to the forward speed problem

The 2-D， non-linear， potential flow gravity wave problem written in a moving coordinate system with constant velocityin thedirection， is expressed by the kinematic and the dynamic free-surface boundary conditions which can be written as:

To apply WENO on the free surface boundary conditions， they have to be expressed in Hamilton-Jacobi form［12］

For the spatial discretization the Lax-Friedrichs scheme is used［13］

The free surface boundary conditions can be expressed in the WENO formulation as:

where

The right hand side terms， namelyand， are considered to be source terms.

The dissipation coefficients are given by

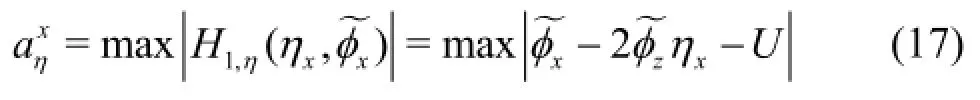
and

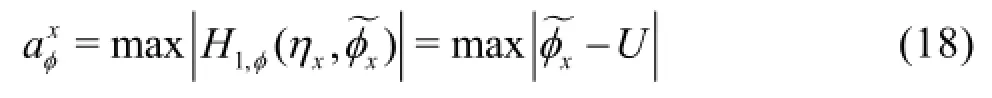
3. Representative test cases

In a general seakeeping problem， waves will travel in all directions at a range of different speeds relative to the ship speed， and the numerical scheme must be able to handle all the possible ship speed to wave celerity ratios. Thus， we test the scheme using a set of deep water waves with， over a range of different ship speed to wave propagation speed ratios. The wave height is 90% of the stable limit，. The different test cases are visualized in Figs.10-15. The wave is propagated for ten periods with a fixed Courant number ofand energy conservation is monitored. The WENO 6 scheme is compared with both centered and upwinded 6th order finite difference schemes. When， upwinding is achieved by shifting the stencil one point to the left. Forthe stencil is shifted one point to the right， whereis the ship speed. The energy conservation is monitored for each simulation and the results are presented in Figs.16-21. The centered scheme is always unstable for convective problems （and therefore not plotted for clarity）. The upwind-biased scheme can handle most cases， but will always become effectively down-winded， and hence unstable， for waves which travel faster than the frame of reference and in the same direction as the frame of reference. In contrast， the WENO scheme is stable in all the tested cases. The dissipation introduced by the WENO scheme is generally as low or lower than the upwindbiased scheme， though for high-accuracy， very highorder schemes may be desirable. It should be noted that the WENO scheme was also tested with the nonlinear weights of Jiang et al.［6］and Borges et al.［10］but both were found to be significantly more dissipative than the ones of Yamaleev and Carpenter［7］. This provides the basis for solving general nonlinear wavestructure interaction problems at forward speed.

Fig.10

Fig.11

Fig.12

Fig.13

Fig.14

Fig.15

Fig.16

Fig.17

Fig.18

Fig.19

Fig.20

Fig.21

4. Conclusion

A new way of deriving finite-difference WENO coefficients has been presented together with a new smoothness indicator that adds flexibility to the schemes and is straight-forward to implement numerically without the need for tabulated coefficients. The method has been tested on the non-linear wave propagation problem in a moving frame of reference which mimics a forward speed seakeeping problem. The proposed high-order WENO scheme remains upwinded and stable under all combinations of wave speed and frame of reference speed. A massively parallel implementation of the method in 3-D in the library of Glimberg et al.［14］and testing with ship geometries is in progress and will be reported on in the near future.

［2］ ENGSIG-KARUP A. P.， MADSEN M. G. and GLIMBERG S. L. A massively parallel gpu-accelerated model for analysis of fully nonlinear free surface waves［J］. International Journal for Numerical Methods in Fluids，2012， 70（1）: 20-36.

［3］ LINDBERG O.， BINGHAM H. B. and ENGSIG-KARUP A. P. Towards real time simulation of ship-ship interaction-Part III: Immersed body boundary condition and double body ship-ship interaction［C］. Proceedings of the 29th International Workshop on Water Waves and Floating Bodies. Osaka， Japan， 2014.

［4］ AFSHAR M. A.， BINGHAM H. B. and READ R. A highorder finite-difference solver for the linearised potential flow wave resistance problem on curvilinear overset grids［C］. Proceedings of the 29th International Workshop on Water Waves and Floating Bodies. Osaka，Japan， 2014.

［5］ BINGHAM H. B.， AFSHAR M. A. and READ R. et al. Stable finite difference discretizations of the forward speed seakeeping problem［C］. Proceedings of the 29th International Workshop on Water Waves and Floating Bodies. Osaka， Japan， 2014.

［6］ JIANG G. S.， PENG D. Weighted ENO schemes for Hamilton-Jacobi equations［J］. SIAM Journal on Scientific Computing， 2010， 21（6）: 2126-2143.

［7］ YAMALEEV N. K.， CARPENTER M. H. A systematic methodology for constructing high-order energy stable WENO schemes［J］. Journal of Computational Physics，2009， 228（11）: 4248-4272.

［8］ JIANG G. S.， SHU C. W. Efficient implementations of Weighted ENO schemes［J］. Journal of Computational Physics， 1995， 126（1）: 202-228.

［9］ BALSARA D. S.， SHU C. W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy［J］. Journal of Computational Physics， 2000， 160（2）: 405-452.

［10］ BORGES R.， CARMONA M. and COSTA B. et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws［J］. Journal of Computational Physics， 2008， 227（6）: 3191-3211.

［11］ BINGHAM H. B.， ZHANG H. On the accuracy of finite difference solutions for nonlinear water waves［J］. Journal of Engineering Mathematics， 2007， 58（1）: 211-228.

［12］ OSHER S.， FEDKIW R. Level set methods and dynamic implicit surfaces［M］. New York， USA: Springer-Verlag，2002.

［13］ CRANDALL M. G.， LIONS P. L. Two approximations of solutions of Hamilton-Jacobi equations［J］. Mathematics of Computation， 1984， 43（167）: 1-19.

［14］ GLIMBERG S. L.， ENGSIG-KARUP A. P. and NIELSEN A. S. et al. Development of software components for heterogeneous many-core architectures. Designing scientific applications on GPUs［M］. Boca Raton， USA: Chapman and Hall/CRC， 2013， 73-104.

References

［1］ ENGSIG-KARUP A. P.， BINGHAM H. B. and LINDBERG O. An efficient flexible-order model for 3D nonlinear water waves［J］. Journal of computational physics，2009， 228（6）: 2100-2118.

November 2， 2015， Revised January 13， 2016）

* Biography: Stavros KONTOS （1985-）， Male，

Ph. D. Candidate