Theoretical study of novel B-C-O compounds with non-diamond isoelectronic

Chao Liu(刘超) and Pan Ying(应盼)

1College of Rare Earths,Faculty of Materials Metallurgy and Chemistry,Jiangxi University of Science and Technology,Ganzhou 341000,China2State Key Laboratory of Metastable Materials Science and Technology,Yanshan University,Qinhuangdao 066004,China3Hebei Key Laboratory of Microstructural Material Physics,School of Science,Yanshan University,Qinhuangdao 066004,China

Two novel non-isoelectronic with diamond(non-IED)B—C—O phases(tI16-B8C6O2 and mP16-B8C5O3)have been unmasked. The research of the phonon scattering spectra and the independent elastic constants under ambient pressure(AP)and high pressure(HP)proves the stability of these non-IED B—C—O phases. Respective to the common compounds,the research of the formation enthalpies and the relationship with pressure of all non-IED B—C—O phases suggests that HP technology performed in the diamond anvil cell(DAC)or large volume press(LVP)is an important technology for synthesis.Both tI16-B8C6O2 and tI12-B6C4O2 possess electrical conductivity.mP16-B8C5O3 is a small bandgap semiconductor with a 0.530 eV gap. For aP13-B6C2O5,mC20-B2CO2 and tI18-B4CO4 are all large gap semiconductors with gaps of 5.643 eV,6.113 eV, and 7.105 eV, respectively. The study on the relationship between band gap values and pressure of these six non-IED B—C—O phases states that tI16-B8C6O2 and tI12-B6C4O2 maintain electrical conductivity, mC20-B2CO2 and tI18-B4CO4 have good bandgap stability and are less affected by pressure. The stress-strain simulation reveals that the max strain and stress of 0.4 GPa and 141.9 GPa respectively, can be sustained by tI16-B8C6O2. Studies on their mechanical properties shows that they all possess elasticity moduli and hard character. And pressure has an obvious effect on their mechanical properties, therein toughness of tI12-B6C4O2, aP13-B6C2O5, mC20-B2CO2 and tI18-B4CO4 all increases,and hardness of mP16-B8C5O3 continue to strengthen during the compression. With abundant hardness characteristics and tunable band gaps,extensive attention will be focused on the scientific research of non-IED B—C—O compounds.

Keywords: stability analysis,pressure,formation enthalpy,property

1. Introduction

Since non-stoichiometric ratio B—C—O ternary compounds have been synthesized via high pressure (HP) experiments in multianvil apparatus with high temperature,[1—3]due to the formation of rigid covalent bonds, the scientific research on design of B—C—O ternary system with high hardness has attracted great enthusiasm.[4—7]As a typical representative (isoelectronic with diamond, short as IED, also the simplest ternary B—C—O compounds), B2CO compounds have become the first to be of concern among all the B—C—O ternary system compounds. After pioneering research,Liet al.exposed two superhard B2CO structures with high hardness about 50 GPa (tP4-B2CO and tI16-B2CO).[4]In fact, more ternary compounds exist in B—C—O systems including B2CXO(X=2,3,4,...),are IED.As the increase of C content will result in the stacking of C in the structure, and forming shorter and stronger sp3C—C bonds. Hence, Liet al.believe that B2CXO (X=2,3,4,...) are extremely likely to have higher hardness than B2CO.[4]

Encouraged by Li’s research, Zhanget al.focused the theoretical research on the B2CXO (X ≥2) system and foretold three new superhard phases:[5]B2C2O with space group(SG)I41/amdis denoted as tI20-B2C2O, B2C3O with SGdenoted as tI12-B2C3O,and tP8-B2C5O for B2C5O with.[5]Based on the theoretical calculation model of hardness proposed by Gaoet al.,[8]tI20-B2C2O,tI12-B2C3O and tP8-B2C5O all have superhard nature with Vickers hardness value significantly exceeding 40 GPa (57 GPa, 62 GPa,and 68 GPa, respectively).[5]The relationship between carbon ratio via mechanical properties of B2CXO was established,and high carbon content improves both the elastic moduli and hardness,[5]which is well confirmed by Li’s conjecture.[4]

Afterward, the B2CXO (X ≥1) series of compounds as the IED B—C—O have received constant attention. Different from those B2CXO (X ≥1) phases with tetragonal structures reported by predecessors,Liuet al.firstly proposed one superhard B2CO phase (oP8-B2CO) with an orthorhombic system,[9]which opens a new structural system for the design of high hardness materials of B—C—O system. Whereafter the physical properties of oP8-,tI16-,and tP4-B2CO under HP have been investigated by Qiaoet al.[10]Inspired by the structural characteristic of newly predicted B—C—O, both tP4-B2CO and tI16-B2CO have diamond-like structures,[4]oP8-B2CO possesses a lonsdaleite-like structure,[9]even tI20-B2C2O, tI12-B2C3O and tP8-B2C5O all share the diamondlike structures and can be derived from different tP4-B2COsupercells with partial B and O replaced by C.[5]Two orthorhombic B2CO phases(oP16-B2CO and oC16-B2CO)with superhard property have been predicted by four-step manual construction,[11]and they share the similar structures to Cco-C8 and Bct-C4,respectively.

Even with great success in structure design,the most stable structure of B2CO in the ground state remains a mystery.To this end, Yanet al.carried out in-depth research and finally identified a novel orthorhombic structure oI16-B2CO as the B2CO thermodynamic ground-state phase via an unbiased structure searching method.[12]Different from these previously proposed phases,oI16-B2CO is formed by covalent sp2—sp3B—C and B—O bonds,and has a considerably lower energy than that of all others.[12]Encouraged by the first sp2and sp3hybridization coexist B2CO structure,a new metastable phase for B2CO (tP16-B2CO) with sp2—sp3coexisted was explored by Chenet al.[13]The calculation of mechanical properties indicates its hard properties with high hardness of 23.19 GPa and anisotropy with the max stress along[001]far larger than that along[100].[13]

However, there are few studies on B—C—O compounds as non-IED. In 2016, Wanget al.initiated the study of nonisoelectronic system among B—C—O compounds and predicted a new superhard phase B4CO4with a body-centered tetragonal structure;[6]here we denoted it as tI18-B4CO4. tI18-B4CO4is metastable under ambient pressure (AP), but thermodynamically stable at HP above 23 GPa.[6]And the thermodynamic stability,mechanical and electronic properties of tI18-B4CO4were systematically studied by Qiaoet al.[14]and Nuruzzamanet al.[15]Also two low-enthalpy metastable compounds(B6C2O5with primitive triclinic structure, B2CO2with (0.5,0.5, 0) centered monoclinic) have been discovered.[6]For unification and ease of description, here named these two as aP13-B6C2O5and mC20-B2CO2, respectively. They can stably exist to HP as 20 GPa, and the hardness of aP13-B6C2O5is 29.6 GPa, which is relatively softer and more easily machinable compared to mC20-B2CO2(41.7 GPa).[16]Two years later, only one non-IED (tI12-B6C4O2) has been reported.[17]And the research about the mechanical properties reveals that tI12-B6C4O2possesses hard nature with hardness of 21.9 GPa.[17]Since then, there has none report of B—C—O compounds with non-IED.

Previous theoretical studies have made good progress in predicting high-performance structures,but have not provided theoretical guidance for experimental synthesis. And then due to stoichiometric ratios B—C—O compounds have not been synthesized experimentally,the research of B—C—O compounds is limited to difficulties. In this paper,we focus on the non-IED B—C—O compounds. Undergoing rigorous structural stability analysis including mechanical and dynamical stabilities, two novel phases were discovered. Together with these previously reported structures,the optimized reactants and HP conditions were obtained based on the formation enthalpies calculation,which will provide guidance for HP experimental synthesis.Based on density function theory, the mechanical and electronic properties of all non-IED B—C—O compounds have been systematically studied,and the regulatory effect of pressure on properties has also been further investigated.

2. Computational methods and details

The potential structures of non-IED B—C—O compounds have been generated through evolutionary simulation methods CALYPSO[18—20]and USPEX.[21—23]The following full relaxation geometry optimizations were performed in CASTEP models.[24]The gradient-corrected functionals adopted the Perdew—Burke—Ernzerhof(PBE)form.[25]The ultrasoft pseudopotentials were adopted with energy cutoff as 380 eV andKpoints were generated by separation as 8π×10−3nm−1.[26]During the geometry optimizations,[27]iterations were continued until the energy did not change beyond 5×10−3meV per atom;force tensor on atoms was less then 0.1 eV/nm;displacement on atoms was no more than 5×10−5nm and stress did not exceed 20 MPa. The phonon calculation was implemented via the finite displacement method[28]and the elastic constants were calculated with 9 patterns generated for each strain and max strain amplitude as 0.009.

The unit cells were adopted within the following research,and the symmetry points and their path for the Brillouin zone are displayed in Table S1. For the body-centered tetragonal(Bct) system as tI12-B6C4O2and tI18-B4CO4, all belongs share the same symmetry points and the path for the Brillouin zone.

3. Results and discussion

3.1. Optimized structure

Two newly discovered B—C—O structures have been proposed and their crystal structures schematic at AP are shown in Fig.1. For the first compound with space group(SG)is a Bct structure containing 16 atoms per unit cell,hence denoted as tI16-B8C6O2. tI16-B8C6O2possess the same symmetry points with tI12-B6C4O2and tI18-B4CO4,as displayed in Table S1. The lattice parametersaandcare 3.650and 7.899,respectively. All B atoms share the equivalent atomic Wyckoff positions 8i(0.243, 0.243, 0.378); and all O atoms occupy 2b(0.5, 0.5, 0), while for C atoms, C1 2a(0, 0, 0);C2 4d(0.5, 0, 0.25). All the atoms formed covalent bonds with heteroatom by sp3hybridization, however O is not directly bonded to C. That is to say, only B—C and B—O bondsformed in tI16-B8C6O2. There are three different kinds of B—C bonds: type I bonds formed by B and C1 atoms with length of 1.578and type II bonds are formed by B and C2 atoms and length of 1.642. The B—O bonds share the uniform length of 1.640. The theoretical densityρof tI16-B8C6O2at AP is 3.007 g/cm3.

Fig.1.Structure graphs for novel non-isoelectronic B—C—O:(a)tI16-B8C6O2 unit cell and(b)mP16-B8C5O3 (2×2×2)supercell at AP.

For the second compound, it belongs to the primitive monoclinic due to the SG asPm, and the unit cell contains 16 atoms, hence denoted as mP16-B8C5O3. The lattice parametersa,bandcare 9.977, 2.638and 4.404, respectively. And the angelβis about 89.16°. Because the symmetry is extremely low, no class of atomic positions are equivalent(Table S2),hence the formed bonds are all different lengths ranging from 1.423to 1.701.For mP16-B8C5O3,it is also a typical structure with sp2and sp3hybridization coexisting. Thereinto,all C atoms are sp3hybridization with 4 B atoms or 3 B atoms and 1 C atom, all O atoms are sp2binding with 3 B atoms, while B atoms can be divided into two categories: sp3hybridized with 2 C atoms and 2 O atoms or 3 C atoms and 1 O atom, sp2binding with 3 C atoms or 2 C atoms and 1 O atom or 2 O atoms and 1 C atom. In addition, due to the high carbon content, there is also C—C bonds in mP16-B8C5O3, which is quite different from the sp2and sp3hybridization coexisting structures as oI16-B2CO[12]and tP16-B2CO.[13]The calculated densityρis 2.791 g/cm3at AP.

3.2. Stability analysis at ambient pressure

The elastic stabilities of tI16-B8C6O2and mP16-B8C5O3at AP are evaluated by the calculation of the independent elastic constantsCijs,as presented in Table 1.

For tI16-B8C6O2, it belongs to tetragonal system with Laue class 4/mmm,Born criteria are listed as[29]

For mP16-B8C5O3with Laue class as 2/m,belonging to a monoclinic system, it has 13 independent elastic constants.The generic necessary and sufficient criterion that all eigenvalues of the elastic matrix are positive is easy to check with simple linear algebra routines.[29]

The elastic matrices are symmetric about the main diagonal, and this symmetric nonzero data is represented by the apostrophe symbol “...”, and the blank cell represents data that is 0. There is no doubt that from the above elastic matrix in Table 1, theCi js satisfy the criteria above, indicating tI16-B8C6O2and mP16-B8C5O3are elastic stable.

Here theCijs of other four previously reported non-IED B—C—O phases at AP have also been calculated,and the corresponding matrices are listed in Table S3. Both mC20-B2CO2and aP13-B6C2O5have low symmetry, the generic necessary and sufficient criterion that all eigenvalues of C be positive is easy to check with simple linear algebra routines.[29]For tI12-B6C4O2, which belongs to tetragonal system with 4/mmmLaue class, the necessary and sufficient conditions for elastic stability are shown as Eq. (1). For tI18-B4CO4, which possess the tetragonal crystal system and Laue class as 4/m, its criterion for elastic stability can also be evidenced by[29]

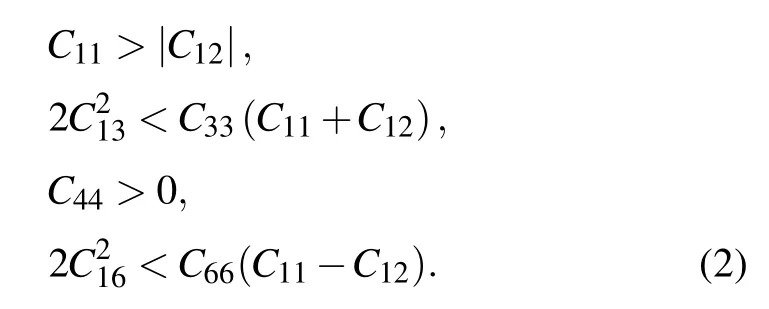
All the independent elastic constants Cijs in the matrices have successfully verified the stability of their elastic, which agree well with the previous research,[6,14,15,17]therefore also proved the accuracy of our calculation methods and parameters.

Table 1. The elastic matrices of two newly non-IED B—C—O phases at AP,the numerical unit is unified with GPa.

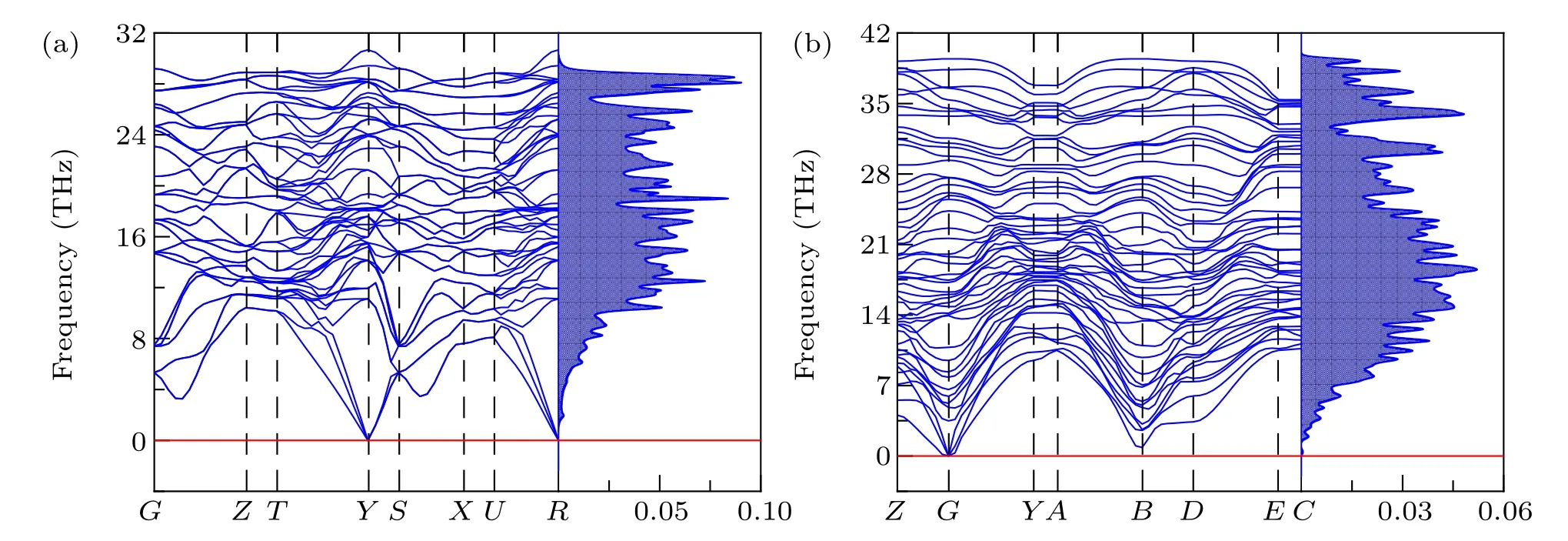
Fig.2. Phonon dispersion spectra and phonon DOS of(a)tI16-B8C6O2 and(b)mP16-B8C5O3 at AP.

Fig. 3. Calculated formation enthalpies ΔHf via the pressure of six non-IED B—C—O compounds, (a)—(c) represent aP13-B6C2O5, mC20-B2CO2 and tI18-B4CO4,respectively. (d)The schematic diagram of LVP and DAC.

The imaginary frequency will lead to crystal distortiom,indicating the dynamical instability. Phonon dispersion spectrum and the related phonon density of states (DOS) of two newly predicted and four reported non-IED B—C—O phases at AP are researched and plotted in Fig. 2 and Fig. S1, respectively. There are no negative phonon modes in the entire Brillouin zone of their unit cell, suggesting they are dynamically stable.

The stability of the newly predicted structures as tI16-B8C6O2and mP16-B8C5O3was further confirmed by molecular dynamics(MD)simulation with a thermostat to maintain a constant temperature of 273 K and with a barostat to maintain a constant AP.The total simulation time is 3 ps and time step as 6 fs. The simulation results are shown in Fig.S2 and there was no significant change in the structure during the whole simulation process. That is,tI16-B8C6O2and mP16-B8C5O3maintain their structural integrity and immutability.

3.3. Potential synthesis reaction

For providing guidance of experimental synthesis,it is of great significance and extremely urgent to deploy the potential synthesis of novel non-IED B—C—O phases. Based on the common reactants such as boron carbide B4C,boron trioxide B2O3, boron-rich oxide B6O, graphite C, andα-boronα-B,constructing different reaction path,then balancing the synthesis equations of these novel non-IED B—C—O phases,therefore the relationships between formation enthalpy ΔHfand pressure are revealed according to the following Eqs. (3)—(13).The ΔHf1and ΔHf2represent the formation enthalpy via path 1 and path 2,respectively. For better comparison and description, these six non-IED B—C—O phases are divided into three groups: tI16-B8C6O2, mP16-B8C5O3; tI12-B6C4O2, aP13-B6C2O5; mC20-B2CO2(treat as B4C2O4), tI18-B4CO4due to the same B ratio.

Figure S3 summarizes the relationships between formation enthalpy (normalized on a per formula) and the pressure of six non-IED B—C—O compounds. The enthalpy of formation is less than zero, indicating the likelihood that the target non-IED B—C—O compounds will be synthesized by the selected reaction, and more negative more possible to be synthesized. Hence the critical pressure for formation enthalpy reaching zero is the key to determining the HP synthesis.

As shown in Fig. S3, the critical pressures of these six non-IED B—C—O compounds have been listed. For tI16-B8C6O2and mP16-B8C5O3, the critical pressures decrease with the C content decrease and O content increase. By comparing the reaction path 1 and path 2,it was found that B6O as one reactant will benefit the decrease of pressure required to react. For tI12-B6C4O2and aP13-B6C2O5, the critical pressures also have similar relationships of C/O content. For the group of mC20-B2CO2and tI18-B4CO4, the conclusion that the critical pressures decrease with the C content decrease are also very well illustrated. Among all the six non-IED B—C—O phases,the max critical pressure is just slightly over 100 GPa.As the working pressure and temperature of the diamond anvil cell (DAC) can reach hundreds of GPa and thousands of degrees centigrade, and the high temperature will benefit to reduce the reaction barrier, hence synergistic high temperature and HP experiments in DAC maybe a potentially efficient synthesis technology for the target B—C—O product at a lower pressure than the theoretical critical pressure value at zero temperature.

For aP13-B6C2O5, mC20-B2CO2and tI18-B4CO4, they all have critical pressures lower than 30 GPa. The relationship between formation enthalpy and pressure in the working pressure range of large volume press (LVP) has been studied in detail. As shown in Fig. 3, for aP13-B6C2O5, mC20-B2CO2and tI18-B4CO4, their critical pressures are 16.5/19.7 GPa,21.4/28.8 GPa, and 4.9 GPa, respectively. This shows that these three non-IED B—C—O structures can be obtained via HP experiments on LVP devices. Of course,special technologies need to be combined,such as rapid pressure relief,rapid cooling and so on,which will help to preserve the new phases.

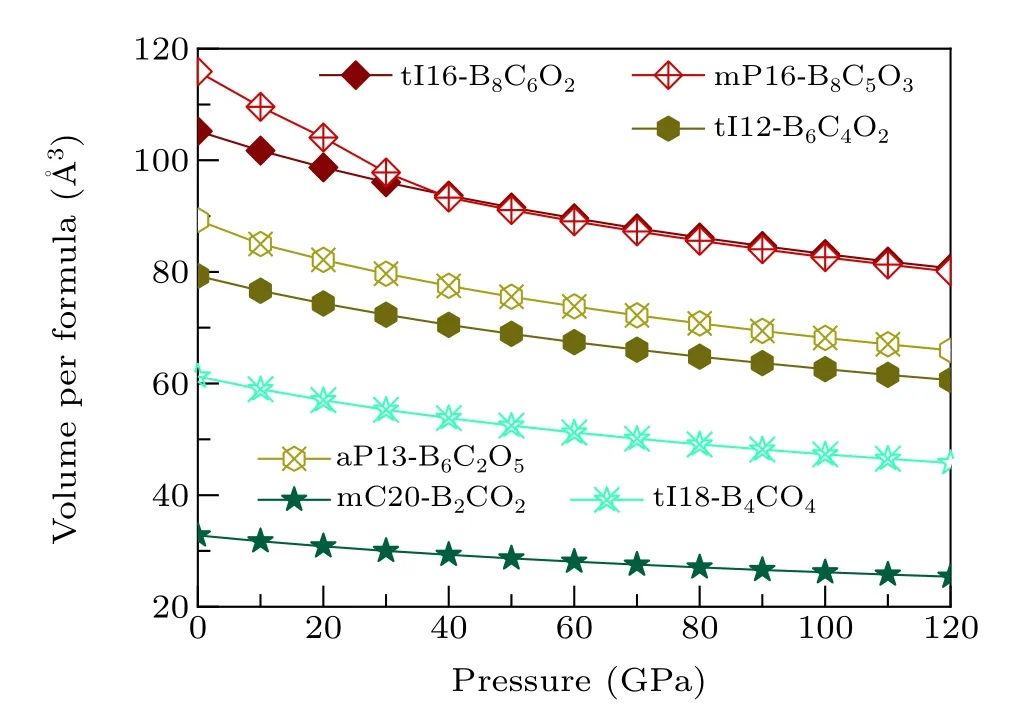
Fig.4. The relationship of pressure and volume per formula of six non-IED B—C—O phases at AP to 120 GPa.

3.4. Stability analysis at high pressure

It is well known that pressure is an important parameter to regulate the state of matter. In general, solid materialsundergo a continuous densification during HP compression.As exhibited in Fig. 4, for these six non-IED B—C—O phases we studied, during the pressure from AP to HP of 120 GPa,the volumes per molecular formula of these phases decrease monotonically. Detailed research has revealed that with the same B proportion,tI16-B8C6O2has the smaller volume drop(24.63/formula) and volume compressibility (23.4%) than mP16-B8C5O3(35.83/formula, 30.9%); tI12-B6C4O2also has a smaller volume decrease (18.73/formula) and volume compressibility (23.6%) than aP13-B6C2O5(23.33per formula, 26.1%); mC20-B2CO2also shares the advantage of resisting volume change(7.43/formula)and volume compressibility (22.6%) than tI18-B4CO4(15.53/formula,25.3%). For mP16-B8C5O3,the volume varies with the pressure in two intervals,with a rapid decline before 40 GPa and a continuous slow decline after 40 GPa.

Fig.5. Calculated phonon and DOS of serval non-IED B—C—O phases at 100 GPa HP;(a)—(e)represent tI12-B6C4O2,aP13-B6C2O5,mC20-B2CO2,tI18-B4CO4 and mP16-B8C5O3,respectively.

As the HP technology is a potential way to synthesize these non-IED B—C—O phases,it is necessary to analysis their stability at HP. The elastic matrix of six non-IED B—C—O phases at HP of 100 GPa are shown in Table S4. All the independent elastic constantCi js satisfy the criteria as Eqs. (1)and (2), or all eigenvalues of elastic matrix are positive, indicating tI16-B8C6O2, mP16-B8C5O3, tI12-B6C4O2, aP13-B6C2O5,mC20-B2CO2and tI18-B4CO4keep elastic mechanical stability at 100 GPa HP.

Their phonon scattering at HP also have been investigated. Figure 5 shows the phonon scattering spectra and DOS of tI12-B6C4O2, aP13-B6C2O5, mC20-B2CO2, tI18-B4CO4and mP16-B8C5O3. No negative frequency is found in the entire Brillouin zone,indicating that these five non-IED B—C—O phases remain stable at 100 GPa. However, as the phonon scattering spectrum and DOS at different pressure exhibited in Fig. S4, for tI16-B8C6O2, when pressure surpasses 80 GPa,negative frequency appears in the phonon spectrum,resulting in HP instability of tI16-B8C6O2. While the pressure is within 80 GPa,tI16-B8C6O2is still stable(no virtual frequency).The independent elastic constant Ci js of tI16-B8C6O2at HP of 40 GPa and 80 GPa have been researched(Table S5),and the related research results show the elastic mechanical stability of tI16-B8C6O2under HP less than 80 GPa. Hence, combining the study of phonon spectrum and elastic constants, the stability of tI16-B8C6O2at HP un-beyond 80 GPa is thoroughly proved.

In fact,the phonon vibration frequency is affected by the strength of chemical bonds. That is the max phonon vibration frequency is an indication of the strength of the chemical bond. Furthermore, zero-point energy is the energy that a quantum will vibrate under the zero point of absolute temperature. The max phonon frequency tells you how strong the bond is. The amplitude of zero-point vibration increases with increasing temperature, and the lighter the atom (that is, the smaller the element number), the more pronounced the zero point vibration. Based on the phonon scattering spectrum and its DOS, zero-point energy can be calculated. Hence, the relationship of max vibration frequency(zero-point energy)and pressure are further researched based on the phonon scattering spectrum and the related DOS at series pressures.

As displayed in Fig. 6, both tI16-B8C6O2and mP16-B8C5O3have max vibration frequency larger than 30 THz,and their max vibration frequencies increases monotonically with increasing pressure. Therein, tI16-B8C6O2has a larger growth range (8.003 THz) and the growth rate (26.1%) than mP16-B8C5O3(6.649 THz, 16.9%). By the comparison of zero-point energy, it was found that even with similar molecular molar mass, the zero point energies of tI16-B8C6O2and mP16-B8C5O3are significantly different, which may be mainly contributed by the structural difference including the density, porosity, and so on. The zero-point energies of tI16-B8C6O2and mP16-B8C5O3continuously increase with the pressure increasing, and the increase range and growth rate of these two phases are 0.578 eV/31.3%and 0.437 eV/20.3%,respectively.

Fig.6. The relationship of pressure and(a)max vibration frequency and(b)zero-point energy of tI16-B8C6O2 and mP16-B8C5O3 at AP to 80 GPa.

3.5. Electrical property

Based on the GGA-PBE functional, the electronic band structures of these six non-IED B—C—O phases along the symmetry points of the Brillouin zone at AP are quickly calculated and displayed in Fig. S5. For tI16-B8C6O2, mP16-B8C5O3and tI12-B6C4O2, there are energy bands that pass through the Fermi level, which indicates that they all possess electrical conductivity. As for the other three, there is no band across Fermi level, and the forbidden bands are formed by valence band max(VBM)and conduction band min(CBM). Hence, for aP13-B6C2O5, mC20-B2CO2, and tI18-B4CO4, they all have semiconductor properties with the gap of 3.927 eV,4.650 eV,and 5.434 eV,respectively.

Although based on the GGA-PBE functional, the electronic band structure can be quickly calculated. However,based on the GGA-PBE functional, the calculated band gap trend to be underestimated. Hence, the more accurate but more time-consuming calculation based on the hybrid functionals HSE06[30,31]is adopted. As shown in Fig. 7, after the rigorous testing of HSE06, both tI16-B8C6O2and tI12-B6C4O2show good electrical conductivity due to the distinct bands cross the Fermi level. For aP13-B6C2O5,mC20-B2CO2and tI18-B4CO4,they all keep semiconductor properties. The max value points in VBM and the min value point in CBM of aP13-B6C2O5are located at high symmetry pointsFandQ, respectively. Hence, aP13-B6C2O5is an indirect bandgap semiconductor with 5.643 eV. For mC20-B2CO2, max VBM locates atZpoint and min CBM does not occupy high symmetry points. It is also an indirect bandgap semiconductor with a gap of 6.113 eV. For tI18-B4CO4, max VBM occupiesGpoints,min CBM locates atMpoint and the value of indirect band gap is as high as 7.105 eV. While, for mP16-B8C5O3,it is an indirect semiconductor with a small gap as 0.530 eV,which is quite different from the conclusion based on GGAPBE. The max VBM and min CBM are located atBandE,respectively.

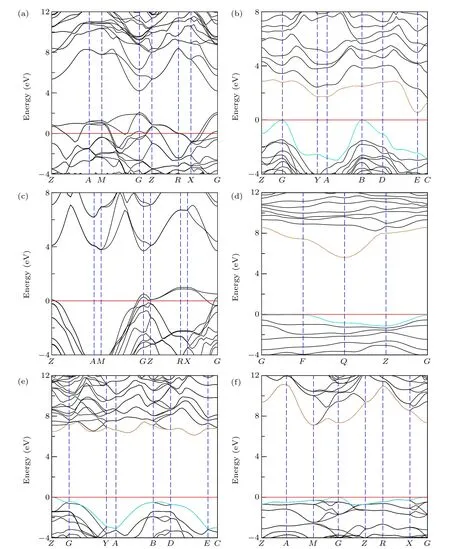
Fig.7.Calculated electronic band structures via HSE06 of non-IED B—C—O phases at AP;(a)—(f)represent tI16-B8C6O2,mP16-B8C5O3,tI12-B6C4O2,aP13-B6C2O5,mC20-B2CO2 and tI18-B4CO4,respectively. The horizontal red line,dark cyan curve and gold curve represent the Fermi energy level,VBM and CBM,respectively.

The relationship between the band gap values and pressure of these six non-IED B—C—O phases was researched.Considering the high computational cost of HSE06 and the research purpose is to reveal the trend of band gap variation with pressure,GGAPBE calculation is adopted here. Both tI16-B8C6O2and tI12-B6C4O2maintain electrical conductivity over the entire pressure range which they are dynamics and elasticity are stable. For the others four phases,the relationship in the range of 0—100 GPa is plotted in Fig.8. For mP16-B8C5O3,it keeps a zero gap until 28 GPa,then the gap rapid increases,however after 36 GPa(gap as 1.113 eV),the band gap sluggishly increases to 1.206 eV with the pressure to 100 GPa. For aP13-B6C2O5,its gap increasessignificantly in the range of AP (3.927 eV) up to 6 GPa (4.227 eV), then the gap increases slowly to 4.330 eV at 100 GPa.However,for mC20-B2CO2and tI18-B4CO4,their gap values both have very slight change during the entail pressure range,the gap value of mC20-B2CO2first goes uphill to 4.695 eV at 10 GPa then downhill to 4.454 eV at 100 GPa,and the gap value of tI18-B4CO4slight increases to 5.496 eV at 50 GPa and then negligible decreases to 5.472 eV at 100 GPa.

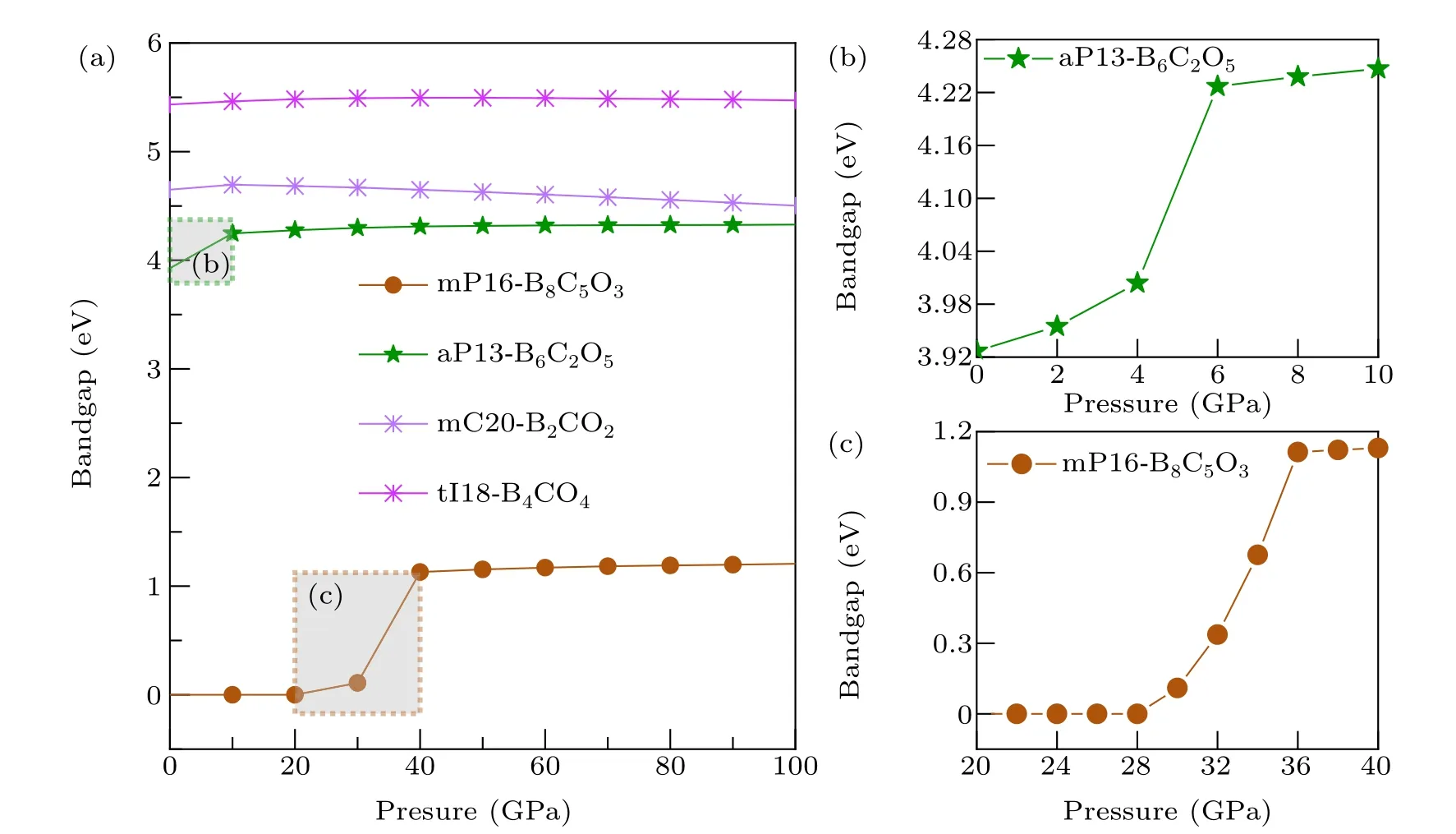
Fig.8. (a)Calculated band gaps as a function of pressure for mP16-B8C5O3,aP13-B6C2O5,mC20-B2CO2 and tI18-B4CO4 based on GGAPBE.Panels(b)and(c)correspond to the dotted areas in(a)with more smaller intervals samples.

3.6. Mechanical property

The material’s ideal strength,which is defined as the critical stress when a perfect crystal lost its elastic stability,equal to the upper limit for material strength. The atomistic mechanism for structural deformation and failure models can be clearly interpretated with the investigation of strain—stress relations and bond-breaking processes.[32]

Figure 9 presents the simulated of tensile stress—strain relationships along the specific directions including[100],[110]and [001] for tI16-B8C6O2. It can be seen that tI16-B8C6O2has the max tensile stress of 141.9 GPa in the [001] direction with the strain at 0.4,which is larger than the max tensile stress (123.1 GPa at strain 0.4) in the [100] direction and the max tensile stress(92.1 GPa at strain 0.275)in the[110]directions. When the strain exceeds 0.4 in the[100]and[001]directions,the tensile tI16-B8C6O2will be destroyed,while for the[110]direction,the largest strain is only about 0.275. For tensile in the[001]direction,the stress and strain increase synchronously,however for[100]and[110]directions,there is a phenomenon of rising first and then falling in the low strain region;then stress and strain increase synchronously in the high strain region. As shown in Table S6,the B—O bonds continue to get longer until the bonds break in any direction we studied,the B—C bonds also get longer monotonous in[001]direction. However,for the[100]and[110]directions,the change of B—C bond is quite complex. In general, with the increase of strain, some B—C bonds continue to get longer, and some B—C bonds experience the process of combination of longer and shorter. During stretching, the bond length changes due to the presence of strain,and the population of the bonds also changes until they break and then the structure will collapse.The calculated strain-stress relations reveal the anisotropy of tI16-B8C6O2.

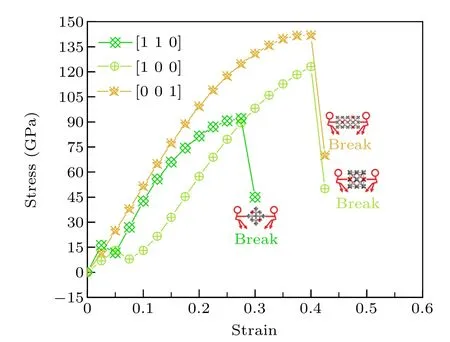
Fig.9. The simulation of tensile stress—strain relationships along the specific direction for tI16-B8C6O2.

As is well-known,bulk modulusB,shear modulusG,and Young modulusEare important parameters to reflect the mechanical properties about the resistance deformation of condensed materials. Generally,Bindicates the ability to resist volume deformation by loading pressure,Grepresents the ability to resist deformation upon shear stress.[33]BandGcanbe acquired by an independent elastic parameter, thenEcan be obtained byBandG. The value ofErepresents the rigidity of the condensed material; the greaterEis,the more difficult it is to deform.

Here the mechanical properties, asB,G, andEof these six non-IED B—C—O phases and their relationship with pressure,are studied in detail. As shown in Fig.10,tI16-B8C6O2has larger elasticity moduli than mP13-B8C5O3at AP. The elasticity moduli of tI16-B8C6O2changes constantly and regularly,the increments ofB,G,andEare 256.6 GPa,139.0 GPa,and 353.9 GPa, respectively. According to data fitting, the modulusBof tI16-B8C6O2and pressurePsatisfies a linear relationship asB=289.54+3.171P. However, as the structure of mP13-B8C5O3changes under pressure, the moduli vary with the pressure also fall in two portions divided by the mutations during 30 GPa to 40 GPa. The moduli’ increments of mP13-B8C5O3are 324.8 GPa (B), 221.7 GPa (G),and 542.0 GPa(E). At 80 GPa HP,the moduli asEandGare an advantage rather than that of tI16-B8C6O2.

Fig. 10. The relationship of pressure and mechanical properties including bulk modulus B, shear modulus G and Young’s modulus E of tI16-B8C6O2 and mP13-B8C5O3. The unit of modulus B,G,and E is unified as GPa.

For the relationship between elasticity moduli and pressure of tI12-B6C4O2and aP13-B6C2O5are plotted in Fig. S6(a), and for mC20-B2CO2and tI18-B4CO4are presented in Fig. S6(b). For modulusEof tI12-B6C4O2go through first rapidly rise then slightly descend, and the max value is 653.5 GPa at pressure of 90 GPa.Except theEof tI12-B6C4O2,all the elasticity moduli of these four B—C—O phases increase monotonically. Compared with the reported bulk modulus of tI18-B4CO4in the range of 0—50 GPa,[15]the similarity of the data and the consistency of the variation indicate the reliability of our calculation. Among all the relationships between moduli and pressure,the linear relationships between moduliBof these four non-IED B—C—O phases and pressurePare more obvious, therein, tI12-B6C4O2:B= 283.90+3.245P;aP13-B6C2O5:B=236.42+3.386P;mC20-B2CO2:B=296.16+3.407P;tI18-B4CO4:B=247.85+3.190P.

The hardness is extensively adopted to evaluate the mechanical properties of condensed matter. Here, the Vickers hardness(HV)of six non-IED B—C—O phases were calculated based on Eq. (14).[34]As reflect the brittleness or toughness of materials,Poisson’s ratioµis also an important mechanical property of materials and can be calculated by Eq. (15). We also studied in detail the effect of pressure on their hardness and Poisson’s ratioµ.

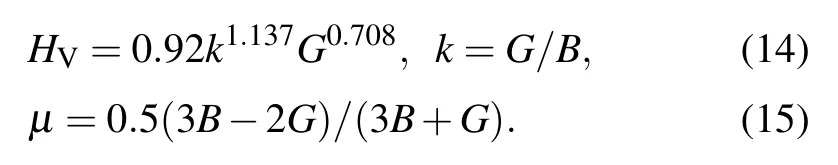
As listed in Table S7,tI16-B8C6O2has high hardness as 21.774 GPa at AP,which is higher than that of mP16-B8C5O3(17.034 GPa). With the increase of pressure, the hardness of tI16-B8C6O2generally increases first and then decreases,and the max value ofHVis 31.808 GPa at 50 GPa. For mP16-B8C5O3,the hardness continues to increase with the pressure increasing. With the increase of pressure, the Poisson’s ratioµof tI16-B8C6O2first decreases and then increases, the min value is 0.223. For the Poisson’s ratioµof mP16-B8C5O3,except for 40 GPa, it also experienced a descent followed by an ascent during the pressure increasing. In the whole pressure range we studied, Poisson’s ratioµof tI16-B8C6O2and mP16-B8C5O3did not exceed the critical value of 0.333,indicating that they both are hard and brittle materials.

For the other four non-IED B—C—O phases, the effects of pressure on Vickers hardnessHVand Poisson’s ratioµare shown in Fig. 11. With loading pressure,HVof mC20-B2CO2and tI18-B4CO4both decrease from 37.919 GPa to 23.809 GPa, and 36.226 GPa to 28.986 GPa, respectively.Based on Eq. (14) and the reported bulk and shear modulus data of mC20-B2CO2under pressure,[16]the effects of pressure on Vickers hardnessHVof mC20-B2CO2can be further developed, and the same downward trend confirms the accuracy of our calculations. The Poisson’s ratioµof mC20-B2CO2and tI18-B4CO4continues to increase.Compared with tI18-B4CO4,mC20-B2CO2has greater variation of Poisson’s ratioµand hardnessHV.

For aP13-B6C2O5,except for the oddity point at 10 GPa,the general trend is either regularly down(HV)or up(µ)with the process of increasing pressure. Based on Eq. (14), it is found that aP13-B6C2O5decreases first and then rises within AP to 20 GPa,[16]this is consistent with the conclusion of our research as the same region,which also proves the complexity of the non-IED B—C—O system and the reliability of the calculation. For tI12-B6C4O2, with the pressure increasing, its hardness first increases from 23.121 GPa(AP)to 25.107 GPa(10 GPa) and then decreases to 16.018 GPa (100 GPa), its Poisson’s ratioµalmost remaining the same at first,and then increase to 0.323, which is closed to the critical value 0.333,indicating that with the increase of pressure,the brittleness of tI12-B6C4O2is weakened and the toughness is strengthened.Our study not only shows their properties at AP, but also explains the law of their mechanical properties effected by pressure.

Fig.11. The relationship of pressure and(a)Vickers hardness HV, (b)Poisson’s ratio µ of tI12-B6C4O2, aP13-B6C2O5, mC20-B2CO2, and tI18-B4CO4.

4. Conclusion

Through the candidate structures generated by evolutionary simulation methods and structural stability analysis by first-principles, two novel non-IED B—C—O phases (tI16-B8C6O2and mP16-B8C5O3) have been unmasked. The research of the phonon scattering spectra and the independent elastic constants under AP and HP also proves the stability of these non-IED B—C—O phases. Respected to the common compounds containing carbon, boron and oxygen, the formation enthalpies and the relationship with pressure of all known(tI12-B6C4O2,aP13-B6C2O5,mC20-B2CO2and tI18-B4CO4) and two newly discovered non-IED B—C—O phases have been systematically studied, and the negative formation enthalpies at specific pressures indicate that HP technology performed in DAC is an important means of synthesizing all non-IED B—C—O phases. Especially, aP13-B6C2O5, mC20-B2CO2and tI18-B4CO4have the possibility of HP synthesis in LVP.

Both tI16-B8C6O2and tI12-B6C4O2possess electrical conductivity.mP16-B8C5O3is an indirect semiconductor with a small bandgap as 0.530 eV. For the aP13-B6C2O5, mC20-B2CO2and tI18-B4CO4are all indirect semiconductors with the gap of 5.643 eV,6.113 eV,and 7.105 eV,respectively. The relationship of band gap values and the pressure of these six non-IED B—C—O phases are researched. Both tI16-B8C6O2and tI12-B6C4O2maintain electrical conductivity. For mC20-B2CO2and tI18-B4CO4,their gap values both have very slight change during the entail pressure range. mP16-B8C5O3and aP13-B6C2O5varies gaps in multiple stages. The stress-strain simulation found that the max stresses for tI16-B8C6O2are 141.9 GPa in the[001]direction with strain 0.4,123.1 GPa in the[100]direction at strain 0.4,and 92.1 GPa in[110]directions at strain 0.275. When the strain/strain exceed this, the tI16-B8C6O2will be destroyed. Studies on their mechanical properties show that they all possess elasticity moduli and hard character. And pressure has an obvious effect on their mechanical properties,therein toughness of tI12-B6C4O2,aP13-B6C2O5, mC20-B2CO2and tI18-B4CO4all increases and hardness of mP16-B8C5O3continue to strengthen during the compression. The enriched mechanical and electronic properties of non IED B—C—O compounds are very likely to attract extensive attention in scientific research and industrial applications.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 12064013), the Natural Science Foundation of Jiangxi Province, China (Grant No. 20202BAB214010), the Open Funds of the State Key Laboratory of Metastable Materials Science and Technology(Grant No.201906),Ganzhou Science and Technology Project(Grant No.202060), and the Program of Qingjiang Excellent Young Talents,Jiangxi University of Science and Technology.