一类新型计算机病毒最优控制模型†

赵夫群

(陕西咸阳师范学院 教育科学学院, 咸阳　712000)



一类新型计算机病毒最优控制模型†

赵夫群†

(陕西咸阳师范学院 教育科学学院, 咸阳712000)

计算机病毒的存在,使得很多计算机无法正常运行,并造成巨大的损失.针对这种情况,提出一类新型计算机病毒的最优控制.控制首先对原有的计算机病毒模型进行改进,加入控制项,提出最优控制问题,并证明最优控制的存在性,然后利用庞德里亚金的极小值原理进行理论分析,最后进行数值模拟.数值模拟结果表明,在没有控制的条件下,原模型得出基本再生数大于1, 说明存在地方病平衡点,并且最终会导致病毒爆发,而数值模拟揭示,运用有效的控制策略能够更好地抑制计算机病毒的传播.

计算机病毒模型,极小值原理,最优控制,数值仿真

引言

计算机病毒是指编制者在计算机程序中插入的破坏计算机功能或者破坏数据,影响计算机使用并且能够自我复制的一组计算机指令或者程序代码.计算机病毒和医学上的“病毒”不同,计算机病毒不是天然存在的,是某些人利用计算机软件和硬件所固有的脆弱性编制的一组指令集或程序代码.它能通过某种途径潜伏在计算机的存储介质或者程序里,当达到某种条件时即被激活,通过修改其他程序的方法将自己的精确拷贝或者可能演化的形式放入其他程序中.从而感染其他程序,对计算机资源进行破坏,所谓的病毒就是人为造成的,对其他用户的危害性很大.计算机病毒的破坏性及传染性对社会造成极大的伤害,仅2008年,计算机病毒在全球造成的经济损失就高达85亿美元.

计算机病毒的传播类似于生物学中病毒的传播方式,通过各种渠道从已被感染的计算机扩散到为被感染的计算机,导致硬盘数据被清空.计算机病毒具有自我复制并传播给其他计算机的功能,同时又有很大的破坏性,一旦计算机被感染上病毒,将可能面临着计算机瘫痪,更严重的甚至会造成社会巨大的经济损失,因此有效预防和控制计算机病毒的传播就显得尤为重要. 生物病毒的最优控制在理论研究方面已经取得很大的成就.比如,艾滋病病毒的最优控制,乙肝,丙肝病毒的最优控制[1-6],由于计算机病毒和生物病毒很相似,很多学者将生物学病毒和杀毒软件结合起来研究计算机病毒模型[7-14]. 虽然控制理论被广泛应用到流行病传播模型中,但是很少学者有研究将控制理论应用到计算机病毒模型中,因此有必要研究一下计算机病毒的最优控制模型.

本文在文献[14]的基础上进行了改进,将之前的常数参数变量变成时变的控制变量,并为新模型建立了最优控制系统. 首先给出控制系统的目标泛函;然后用Pontryagin极小值原理[15-17]推导出最优控制;最后数值仿真验证了所得结论.

1　计算机病毒模型

1.1计算机病毒模型的提出

考虑计算机网络由若干个节点组成的,并且所有的未感染的计算机都可能受到恶意软件的攻击.当恶意软件攻击计算机网络时,一部分节点会被感染.这些感染的节点又会继续感染健康的节点,因此被感染的节点的数目会大量增加.杀毒软件的使用,能够有效的防治计算机病毒的传播,所以文献[14]提出了如下的计算机模型:

(1)

1.2改进的计算机病毒模型

由于现实生活中计算机之间也可以进行病毒传播,所以本文在文献[14]的基础上增加一项β1SI,得到的改进模型如下:

(2)

系统(1)由四部分组成: S表示没有感染病毒但很容易感染病毒的节点; I表示已经感染病毒的节点; M表示网络中恶意对象; P表示杀毒软件. 系统中参数含义: A表示计算机的输入率,β1表示计算机之间病毒感染率,β2表示恶意对象入侵计算机的感染率,γ表示杀毒率,d表示断网率,α表示大量病毒入侵计算机瘫痪率,δ表示病毒复制能力,μ表示病毒入侵率,μ0表示杀恶意对象的效率,η表示杀毒软件的增长率,η0表示杀毒失败率,P0表示计算机现有的杀毒能力.

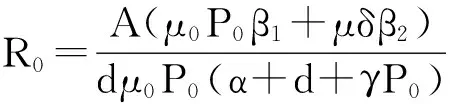
2　最优控制问题

系统(1)中γ和μ0是个常数,本文对此再次改进,将γ和μ0改成控制变量函数θu(t)和u(t).因为γ和μ0是常数的话,会使得控制的成本大大增加,变成时变的控制变量,可以保证在控制计算机病毒减少到很低甚至到零的成本远远低于常数变量.带有控制变量的控制模型如下:

(3)

其中0≤u(t)≤1,θ表示杀毒率调节系数,u(t)表示杀毒率,这里假设杀毒率和购买和更新的杀毒软件的数量成正比.

首先,为了建立最优控制系统,对于给定的整数T>0,给定下列集合作为控制集:

U={u(t)∈L2(0,T): 0≤u(t)≤1,0≤t≤T}

(4)

其次,目标泛函定义如下:

(5)

这样的目标函数是为了通过控制使得感染的计算机和恶意对象的数量达到最小,并且系统的消耗最少,从而达到最优控制的目的,这也是符合我们最优控制的初衷.

初始条件为:

S(0)=S0, I(0)=I0, M(0)=M0,

P(0)=P0.

(6)

下面给出最优控制问题的Lagrangian函数,

L(I,u)=b1I2+b2M2+b3u2,

(7)

其中I,M表示t时刻I和M的数目,u表示为了减少I和M所付出的系统消耗.例如我们用于购买和更新杀毒软件所需要的金钱.

为了寻找目标泛函式(5)的最小值,先定义Hamiltonian函数如下:

H=b1I2+b2M2+b3u2+λ1(A-β1SI-β2SM+

θu(t)IP-dS)+λ2(β1SI+β2SM-

θu(t)IP-dI-αI)+λ3(δμI-u(t)MP)+

λ4(ηI-η0(P-P0)).

(8)

3　最优控制存在性

最优控制的存在性证明:

由文献[15],且方程(3),(4), (6)满足如下条件:

1) 控制集和相对应的状态变量集为非空集合.

2) 可测集U是闭的凸集.

3) 系统(3)方程的右边关于u的线性函数,并且是连续有界的.

4) 目标泛函的被积函数L(I,u)在U上式凹函数.

综述,系统(2)存在最优控制.

利用Pontryagin的极小值原理[16],极小值原理的必要条件如下:

7) S(0)=S0,I(0)=I0,M(0)=M0,P(0)=P0.

9) λi(T)=0, i=1,2,3,4.

得出使目标泛函式(4)到达最小值的一个最优控制为

(9)

4　数值模拟和分析

根据前面的理论分析,本文通过实验来验证使用适当的控制策略之后,计算机病毒传播将得到有效控制.并将杀毒率分别是常数和变量函数进行比较,从图中看出控制模型能够更加有效地抑制病毒的传播.

给定初始条件如下:

S(0)=0.2,I(0)=0.3,M(0)=0.3,P(0)=0.2,经过对模型的初始条件及相关参数进行多次试验后,选取了如下参数:

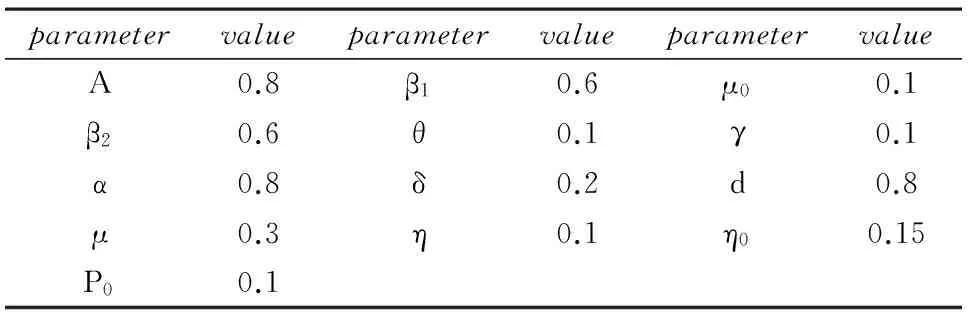
表1　数值模拟参数

图1　控制前后易感电脑S的趋势变化

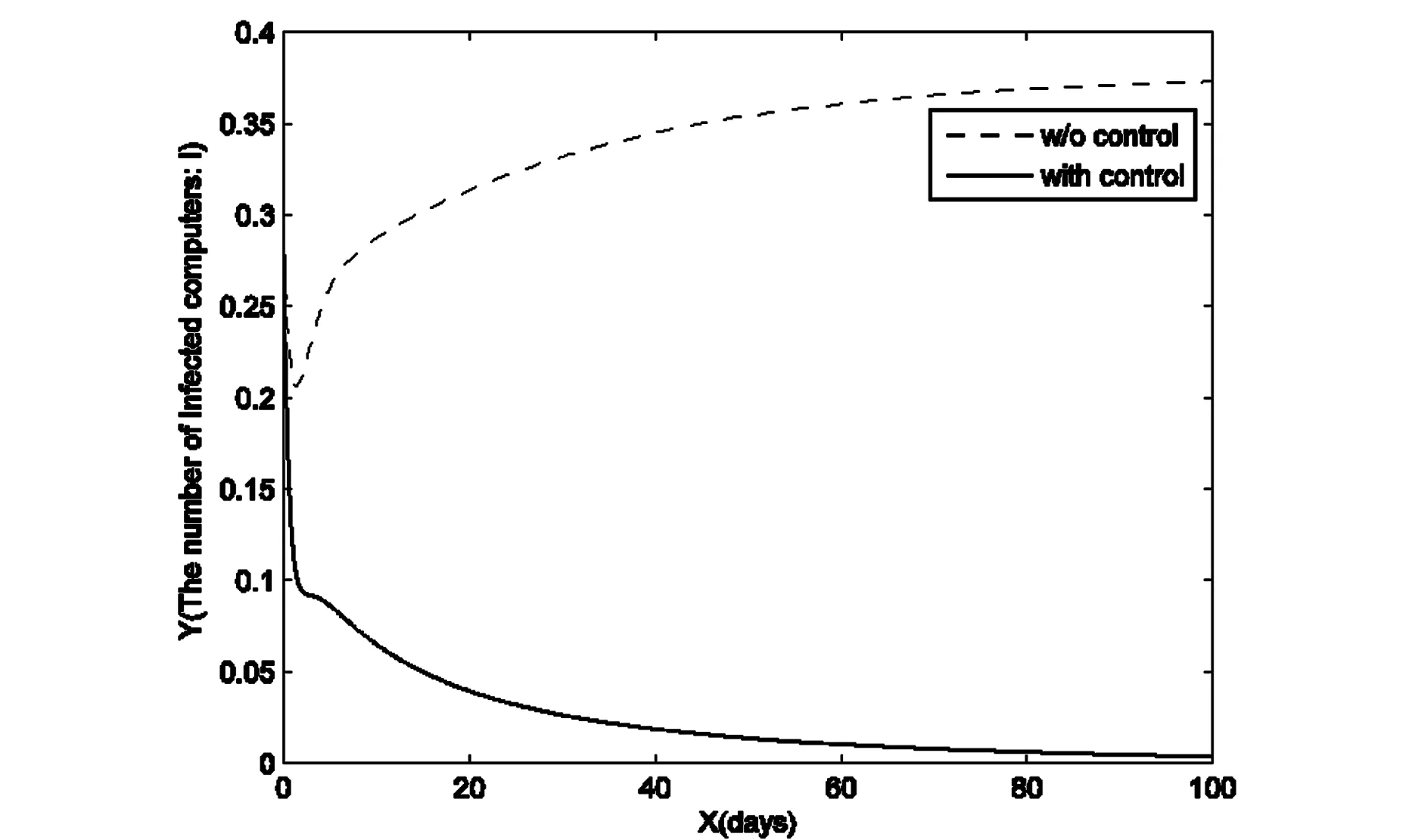
图2　控制前后被感染的电脑I的趋势变化Fig.2　The number of infected computers with control and without control

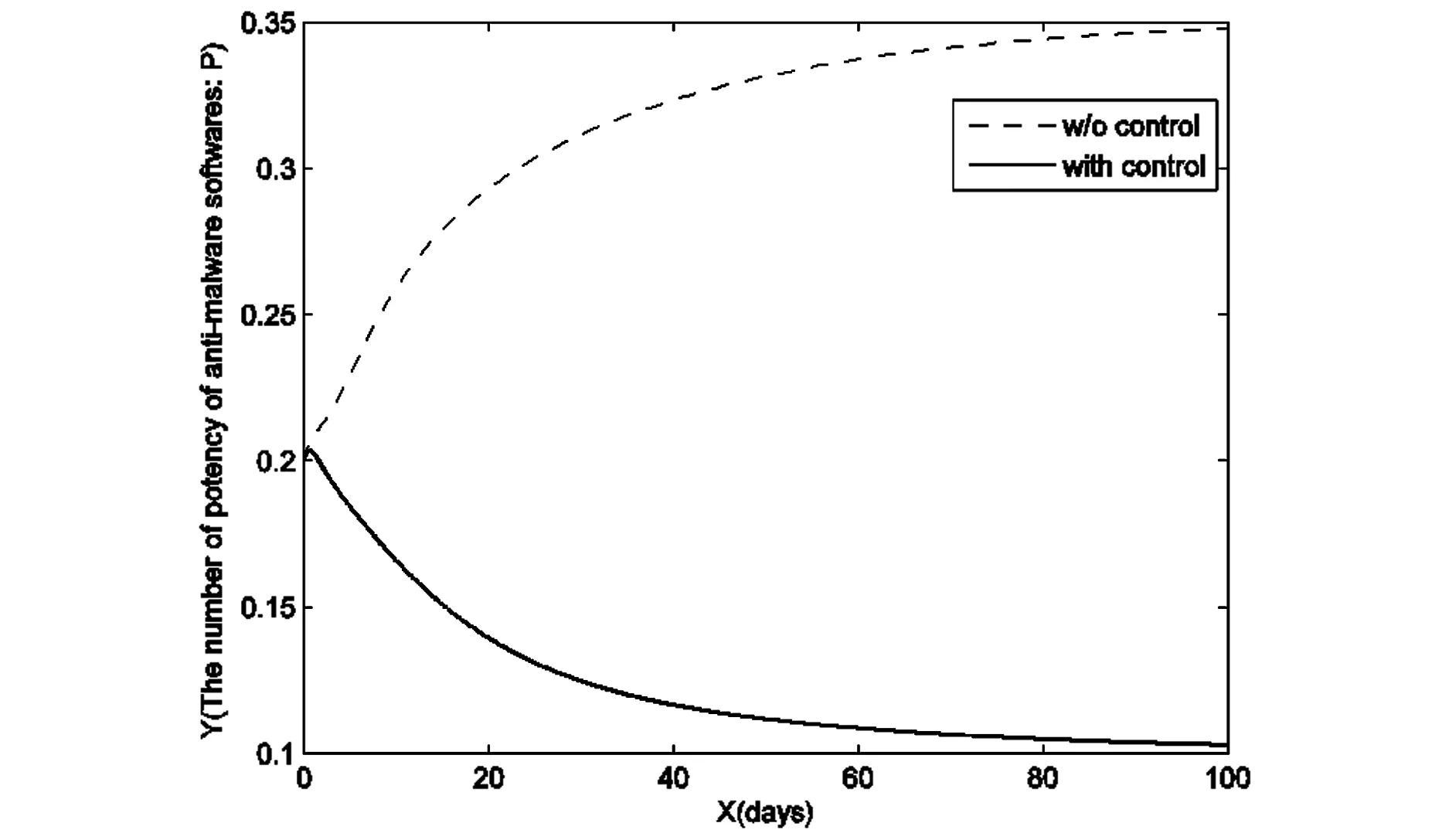
图4　控制前后杀毒软件P的趋势变化Fig.4　The number of anti-malicious software with control and without control

图5　控制变量曲线

5　结语

通过上面的数值模拟可以很明显的看到,在有最优控制条件下,易感染的计算机的数量和被感染的计算机的数量趋势是符合目标函数的预期,而在没有控制的条件下,计算机病毒的传播无法被控制.从控制量的走势也可以明显看到,并不需要一直持续的最大效力就可以将计算机病毒的传播控制住,这也是符合最优控制的目标:在费用最小的前提下,被感染的计算机的数量最少.研究计算机病毒模型是为了更好地控制计算机病毒的传播,在此目的上,本文建立一个新的计算机病毒最优控制模型,通过有效的控制策略,成功地将感染病毒的节点控制在一个较低的水平,利用数值模拟进一步揭示了使用适当的控制方法之后,能够有效控制计算机病毒的传播,并且在有控制的条件下得到的效果比没有控制的条件下的模型的效果好,这也说明研究带有控制的计算机病毒模型更具有实际意义.

1PachputeG,ChakrabartySP.DynamicsofhepatitisCunderoptimaltherapyandsamplingbasedanalysis. Communications in Nonlinear Science and Numerical Simulation, 2013,18(8):2202～2212

2MouofoPT,TewabJJ,MewoliB,BowongS.Optimalcontrolofadelayedsystemsubjecttomixedcontrol-stateconstraintswithapplicationtoawithin-hostmodelofhepatitisvirusB. Annual Reviews in Control, 2013,37(2):246～2593CostanzaV,RivadeneiraPS,BiaforeFL.OptimizingthymicrecoveryinHIVpatientsthroughmultidrugtherapies. Biomedical Signal Processing and Control, 2013,8(8):90～974LashariAA,ZamanG.Optimalcontrolofavectorbornediseasewithhorizontaltransmission. Nonlinear Analysis: Real Word Applications, 2012,13(1):203～212

5BlaynehKW,CaoY,KwonHD.Optimalcontrolofvector-bmediseases:treatmentandprevention. Discrete and Continuous Dynamical Systems-Series B, 2009,11(3):587～611

6JungIH,KangYH,ZamanG.OptimaltreatmentofanSIRepidemicmodelwithtimedelay. Biosystems, 2009,98(1):43～50

7MishraBK,JhaN.Fixedperiodoftemporaryimmunityafterrunofanti-malicioussoftwareoncomputernodes. Applied Mathematics and Computation,2007,190(2):1207～12128YangLX,YangXF.Thespreadofcomputervirusesundertheinfluenceofremovablestoragedevices. Applied Mathematics and Computation, 2012,219(8):3914～3922

9FengLP,HanQ,WangHB,etal.EffectiveimmunemeasuresonP2Pbotnets. Journal of Computer Application, 2012,32(9):2617～2619,2623

10BillingsL,SpearsWM,SchwartzIB.Aunifiedpredictionofcomputervirusspreadinconnectednetworks. Physics Letters A, 2002,297(6):261～266

11MishraBK,SainiD.Mathematicalmodelsoncomputerviruses. International Journal of Applied Mathematics and Computer Science, 2007,187(2):929～936

12YangLX,YangXF,ZhuQY,etal.Acomputervirusmodelwithgradedcurerates. Nonlinear Analysis: Real World Applications, 2013,14(1):414～422

13陈方方,洪灵.一类具有时滞和非线性发生率的SIRS传染病模型稳定性与Hopf分岔分析.动力学与控制学报,2014,12(1):79～85 (ChenFF,HongL.StabilityandhopfbifurcationanalysisofadelayedSIRSepidemicmodelwithnonlinearsaturationincidence. Journal of Dynamics and Control, 2014,12(1):79～85 (inChinese))14MisraAK,VermaM,SharmaA.Capturingtheinterplaybetweenmalwareandanti-malwareinacomputernetwork. Applied Mathematics and Computation, 2014,229:340～349

15KamienMI,SchwartzNL.Dynamicsoptimization:thecalculusofvariationsandoptimalcontrolineconomicsandmanagement.Netherland:ElseverScience, 2000

16QiXH,HuangJQ,DongHR,YangZJ.Moderncontroltheoryandapplications.Beijing:NationalDefenceIndustryPress, 2007:186～191

17张旭龙,杨小帆.计算机病毒的最优控制模型.计算机应用研究,2011,28(8):3040～3043 (ZhangXL,YangXF.Optimalcontrolforcomputerviruses. Applied Research of Computers, 2011,28(8):3040～3043 (inChinese))

*Researchon3DreservoirdataprocessingbasedonArtificialIntelligence

†CorrespondingauthorE-mail:13240766843@163.com

29July2014,revised19May2015.

ANOPTIMALCONTROLMODELFORANEWTYPEOFCOMPUTERVIRUS†

ZhaoFuqun†

(Xianyang Normal University, College of Education Science, Xianyang712000, China)

Duetotheexistenceofcomputervirus,largenumbersofcomputerscannotrunnormally.Itusuallyresultsinhugeloss.Tothisend,ancontrolmodelforanewtypeofcomputervirusbasedonageneralcomputervirusmodelisproposedinthispaper.Firstly,anewtypeofcomputervirusmodelisimproved,andthecontrolistakenintoaccount.Theoptimalcontrolproblemisthenproposed.Meanwhile,theexistenceofoptimalcontrolisproved.Pontryagin’sminimalprincipalisemployedtoanalyzetheoptimalcontrol.Finally,thetheoryanalysisisalsosupplementedasacomparisonwork.Thesimulatingresultsshowsthatundertheconditionwithoutcontrol,thebasicreproductivenumberisobtainedfromtheoriginalmodel,anditisbiggerthan1.Moreover,aboveconclusionindicatesthatthereexiststheendemicequilibrium,anditleadstotheoutbreakofthecomputervirusfinally.Thenumericalmodelingshowsthatthroughtheoptimalcontrolstrategy,thespreadofcomputerviruscanbepreventedeffectively.

computervirus,minimumprincipal,optimalcontrol,numericalsimulation

E-mail:13240766843@163.com

10.6052/1672-6553-2015-036

2014-07-29收到第1稿,2015-05-19收到修改稿.

*基于人工智能的三维油藏数据处理研究(07XSYK224)