长短波相互作用方程组的无穷序列新解†

阿如娜　套格图桑

(内蒙古师范大学数学科学学院, 呼和浩特　010022)



长短波相互作用方程组的无穷序列新解†

阿如娜†套格图桑

(内蒙古师范大学数学科学学院, 呼和浩特010022)

本文对长短波相互作用方程组作行波变换后转化成第一种椭圆方程,利用第一种椭圆方程的解和Bäcklund变换,构造了长短波相互作用方程组的无穷序列新解.这里包括了椭圆函数解、双曲函数解、指数函数解和有理函数解.

第一种椭圆方程,无穷序列新解,Bäcklund变换

引言

(1)

这里ψ(x,t)便是长波的振幅,v(x,t)表示短波包络.

一直以来,有许多关于长短波相互作用方程组的研究.如,文献[2]中利用F-展开法获得了方程(1)的由Jacobi椭圆函数表示的周期波解;文献[3]中推广了Jacobi椭圆函数展开法[4]得到了长短波相互作用方程的准确包络周期解;文献[5]中利用多项式完全判别系统方法[6-12]得到了方程(1)的所有单行波解的分类,这些解包括三角函数、双曲函数和椭圆函数解.

文献[5]获得了长短波交互系统的由三角函数、双曲函数和椭圆函数组成的有限多个解.本文通过行波变换,将方程(1)转换成了第一种椭圆方程,进而利用第一种椭圆方程的解和Bäcklund变换构造了方程(1)的无穷序列新解.

1　第一种椭圆方程的解和Bäcklund变换

1.1第一种椭圆方程(2)的解

(2)

文献[13]给出第一种椭圆方程(2)的下列解.

情况1.当A=1,B=-1-k2,C=k2时,(3)～(4)式是第一种椭圆方程(2)的解：

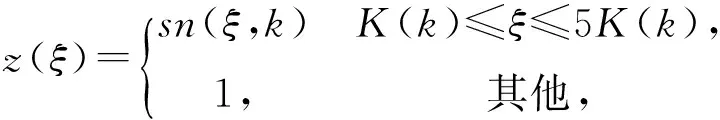
(3)

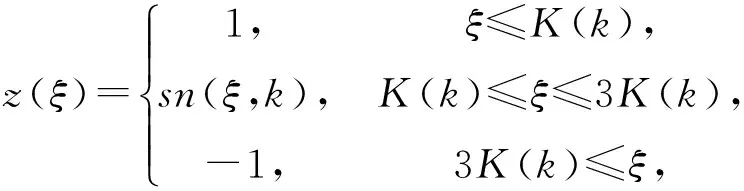
(4)

情况2.当A=1-k2,B=2k2-1,C=-k2时,得到第一种椭圆方程(2)的如下解：

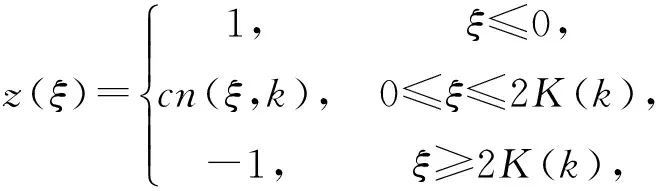
(5)

情况3.当A=-1+k2,B=2-k2,C=-1时,获得了第一种椭圆方程(2)的下列解：

(6)

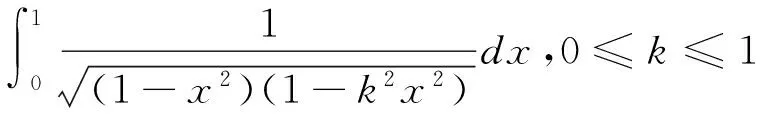
情况4.当A=0时,获得了第一种椭圆方程(2)的如下形式的解：

(7)

(8)

(9)

情况5.当B2-4AC=0时,得到第一种椭圆方程(2)的如下解：

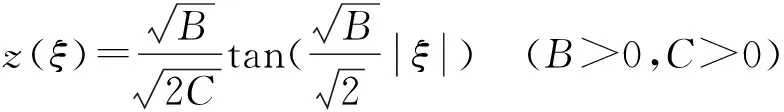
(10)

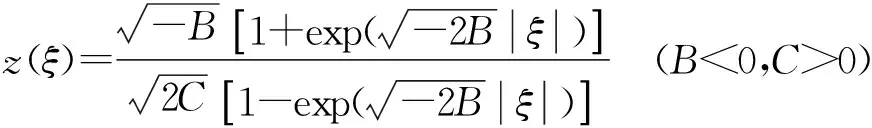
(11)

情况6.当A=B=0时,(12)式是第一种椭圆方程(2)的解：

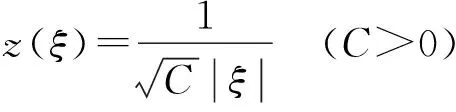
(12)

1.2第一种椭圆方程的Bäcklund变换

若zn-1(ξ)(n=1,2,…)是第一种椭圆方程(2)的解,则下列zn(ξ)(n=1,2,…)也是第一种椭圆方程(2)的解.

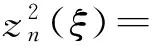
(13)

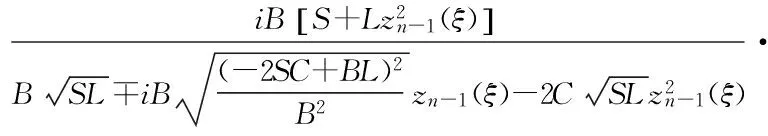
(B2-4AC=0),

(14)

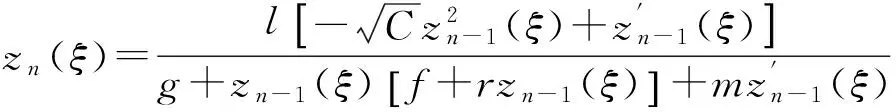
(A=B=0).

(15)

其中SL<0,l,m,g,f,r是任意常数,A,B和C是方程(2)的系数.

2　方程(1)的无穷序列新解

对方程(1)作行波变换

(16)

后,得到如下方程

c=2p,

(17)

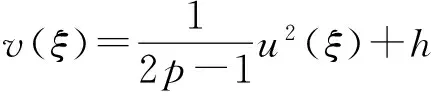
(18)

u″(ξ)-u(ξ)v(ξ)-(p+q2)u(ξ)=0,

(19)

这里p,q和c是待定常数,h是积分常数.

将式(18)代入式(19),化简后用u′(ξ)乘以方程的两边,并对ξ积分一次后得到下列方程

(u′(ξ))2=a+bu2(ξ)+du4(ξ),

(20)

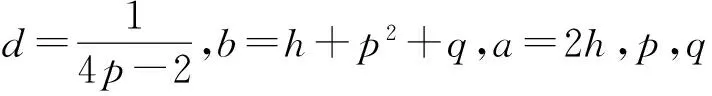
观察方程(20)后得知,方程(20)是第一种椭圆方程.由上面提到的第一种椭圆方程(2)的解和Bäcklund变换可得到方程(20)的无穷序列新解.

情况1.长短波相互作用方程组(1)的椭圆函数型无穷序列解

通过下列迭代公式可得到长短波相互作用方程组(1)的椭圆函数型无穷序列解.

(21)

情况2.长短波相互作用方程组(1)的双曲函数型无穷序列解

利用以下公式,可构造长短波相互作用方程组(1)的双曲函数型无穷序列解.

(22)

情况3.长短波相互作用方程组(1)的指数函数型无穷序列解

由式(11),(14),(16)和(17),可得到长短波相互作用方程组(1)的指数函数型无穷序列解.

(23)

情况4.长短波相互作用方程组(1)的有理函数型无穷序列解

通过下列叠加公式,可获得长短波相互作用方程组(1)的有理函数型无穷序列解.

(24)

SL<0,l,m,g,f,r,p,q,h,c是任意常数,a,b和d是方程(20)的系数.

3　结论

文献[5]得到了长短波相互作用方程组(1)的三角函数、双曲函数和椭圆函数解,也包含了文献[1]中获得的解.本文利用行波变换将长短波相互作用方程组(1)转化成了第一种椭圆方程,进而利用第一种椭圆方程的解和Bäcklund变换构造了长短波相互作用方程组(1)的椭圆函数型、双曲函数型、指数函数型和有理函数型的无穷序列新解.

1Bekir A, Ayhan B, Ozer M N. Explicit solutions of nonlinear wave equation systems.ChinesePhysicsB,2013,22(1):010202～010208

2聂慧,王明亮. 长短波相互作用方程组的周期波解.河南科技大学学报(自然科学版),2005,26(1): 0087～0090 (Nie H, Wang M L. Periodic wave solutions for long-short wave interaction equations.JournalofHenanUniversityofScienceandTechnology(NaturalScience),2005,26(1):0087～0090 (in Chinese))

3周国中,郭冠平. 长短波相互作用方程Jacobi椭圆函数新的展开法求解. 浙江师范大学学报(自然科学版),2005,28(1):25～28 (Zhou G Z, Guo G P. The new Jacobi elliptic function expansion method by the long-short wave interaction equation.JournalofZhejiangNormalUniversity(NaturalScience), 2005,28(1):25～28 (in Chinese))

4高翔,化存才. 时变系数下耦合KdV和Burgers方程组的孤波解, 动力学与控制学报,2014,12(4):295～303 (Gao X, Hua C C. Solitary wave solutions for coupled kdv-burgers equations with variable coefficients.JournalofDynamicsandControl,2014,12(4):295～303 (in Chinese))

5Fan H L, Fan X F, Li X. On the exact solutions to the long-short-wave interaction system.ChinesePhysicsB,2014,23(2):25～28

6Liu C S. Classification of all single travelling wave solutions to Calogero-Degasperis-Focas equation.CommunicationsinTheoreticalPhysics, 2007,48(4):601～604

7Liu C S. All single traveling wave solutions to (3+1)-dimensional Nizhnok-Novikov-Veselov equation.CommunicationsinTheoreticalPhysics, 2006,45(6):991～992

8Liu C S. The classification of travelling wave solutions and superposition of multi-solutions to camassa-holm equation with dispersion.ChinesePhysics, 2007,16(7):1832～1837

9Liu C S. Representations and classification of traveling wave solutions to sinh-GSrdon equation.CommunicationsinTheoreticalPhysics, 2008,49(1):153～158

10Liu C S. Solution of ODEu″+p(u)(u′)2+q(u)=0 and applications toclassifications of all single travelling wave solutions to nonlinear mathematical physics equations.CommunicationsinTheoreticalPhysics, 2008,49(2):291～296

11Liu C S. Travelling wave solutions of triple sine-gordon equation.ChinesePhysicsLetters,2004,21(12):2369～2371

12Liu C S. Exact travelling wave solutions for (1+1)-dimensional dispersive long wave equation.ChinesePhysics,2005,14(9):1710～1715

13套格图桑. 论非线性发展方程求解中辅助方程法的历史演进. 北京：中央民族大学出版社,2012:328～331 (Taogetusang. Historical evolution of auxiliary equation method for solving nonlinear evolution equations. Beijing: The press of the minzu university of China, 2012,328～331(in Chinese))

*Project supported by the Natural Natural Science Foundation of China(11361040),the Science Research Foundation of Institution of Higher Education of Inner Mongolia Autonomous Region, China(NJZY16180) and the Natural Science Foundation of Inner Mongolia Autonomous Region,China(2015MS0128)

† Corresponding author E-mail: 369708905@qq.com

09 December 2014,revised 10 August 2015.

NEW INFINITE SEQUENCE SOLUTIONS OF LONG-SHORT-WAVE INTERACTION EQUATIONS†

Aruna†Taogetusang

(CollegeofMathematicalScience,InnerMongoliaNormalUniversity,Huhhot010022,China)

The paper firstly obtained the first kind of elliptic equation for the long-short-wave interaction equations through travelling wave transformation. Based on the solutions and Bäcklund transformation of the first kind of elliptic equation, the new infinite sequence solutions of the long-short-wave interaction equations were constructed, including the Jacobi elliptic function, hyperbolic function, exponential function and rational function.

the first kind of elliptic equation,new infinite sequence solutions,Bäcklund transformation

E-mail: 369708905@qq.com

10.6052/1672-6553-2015-076

2014-12-09收到第1稿,2015-08-10收到修改稿.

*国家自然科学基金资助项目(11361040)、内蒙古自治区高等学校科学研究基金(NJZY16180)和内蒙古自治区自然科学基金资助(2015MS0128)