用谐波-能量平衡法求解单摆方程†
2016-10-17李银山李彤韦炳威李欣业
李银山 李彤 韦炳威 李欣业
(1. 河北工业大学机械工程学院力学系, 天津 300130) (2. 华东理工大学承压系统与安全教育部重点实验室, 上海 200237)
用谐波-能量平衡法求解单摆方程†
李银山1*李彤2韦炳威1李欣业1
(1. 河北工业大学机械工程学院力学系, 天津300130) (2. 华东理工大学承压系统与安全教育部重点实验室, 上海200237)
应用谐波-能量平衡法求解了强非线性单摆方程,谐波-能量平衡法与经典的摄动法和谐波平衡法不同,不是把微分方程和初始条件分离处理;而是把微分方程和初始条件同时处理.用谐波平衡,将描述动力系统的二阶常微分方程,化为以角频率、振幅为变量的非线性代数方程组,考虑能量平衡,构成角频率、振幅为变量的封闭方程组求得解析解.谐波-能量平衡法将谐波平衡与能量平衡相结合,克服了二者的缺点吸取了二者的优点.实例表明,谐波-能量平衡法方法简单,取较少谐波就可以达到较高的精度.
强非线性,单摆,谐波-能量平衡法
引言
角频率是描述周期振动的最主要因素,采用通常的摄动法[1-2]不能求解强非线性振动问题.近三十多年来,强非线性振动研究所取得的一系列成果,其突破点一般最终都可导出振动频率的瞬变性.比如时间变换法,椭圆函数法,频闪法,推广L-P法,等效线性化方法,改进的多尺度法 ,FFT快速Galerkin法,增量谐波平衡法和摄动增量法等[3-6].
张琪昌[7]等将待定固有频率法与规范性方法相结合研究强非线性振动问题的求解.

李银山2005年提出了求解强非线性振动问题的谐波-能量平衡法[13],其关键是采用谐波平衡加能量平衡构成封闭的非线性代数方程组进行求解.文献[14-15]研究了采用谐波-能量平衡法求解对称强非线性动力系统问题.文献[16]研究了采用谐波-能量平衡法求解非对称强非线性动力系统问题.
本文采用谐波-能量平衡法对强非线性单摆方程进行求解研究,并与KBM法进行了对比.
1 谐波-能量平衡法
谐波-能量平衡法的基本思想是把非线性微分方程组的解,用等效的线性微分方程组的解来解析逼近.首先采用谐波平衡,得到以振幅,角频率为未知数的不完备非线性代数方程组(方程数小于未知数);然后利用能量守恒原理,增加关于初始条件、振幅,角频率之间协调的补充方程,从而构成了关于振幅,角频率为未知数的完备非线性代数方程组;对这个非线性代数方程组进行求解,就可以得到近似解析解.
研究形如

(1a)
的振动系统.这里,f(x)是其变量的非线性奇函数.初始条件为:
(1b)
强非线性自由振动微分方程(1),如用一个等效的线性微分方程
(2a)
来代替.保持初始条件相同

(2b)
保持轨道的周期相同,能量相同.即
(2c)
H是系统的哈密顿能量函数,h=const.设方程(1)的近似解析解为
(3)
将方程(1)式中的函数f(x)展开成傅里叶级数
(4)
其中傅里叶系数为:
(5a)
(5b)
(5c)
其中ψ=ωt.
1.1单项谐波-能量平衡法
设对称性方程(1)的解为
x=a1cosψ+b1sinψ
(6)
用Ritz-Galerkin平均法:
(7a)
(7b)
根据能量平衡式(2c),得初始条件的约束方程为
(8)
由(7),(8)联立可解得ω,a1,b1.
1.2两项谐波-能量平衡法
设对称性方程方程(1)的解为:
x=a1cosψ+b1sinψ+a3cosψ+b3sinψ
(9)
令ψ=ωt用Ritz平均法便有:
(10a)
(10b)
根据能量平衡式(2c),得初始条件的约束方程为:
(11)
由(10),(11)联立可解得ω,a1,b1,a3,b3.
2 单摆振动的周期解
2.1振动问题分类
单摆也称为数学摆,其运动方程为
(12)
初始条件为:
(13)
其中固有角频率和周期
(14)

(15)

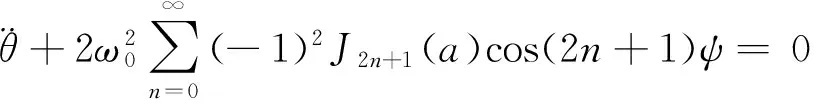
ψ=ωt-φ
(16)
其中Jk(a)为贝塞尔函数.

(17)
这是线性振动方程.方程(17)的解为
θ=acosψ
(18a)
其中:
(18b)
振动周期为
(18c)
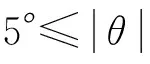
(19)
这是弱非线性振动方程(一般要求0<ε≪1,这里ε=1/6),即著名的软弹簧Duffing方程.


ψ=ωt-φ
(20)
这是不需要考虑小参数的振动方程,称为强非线性振动方程.
KBM法第一次近似解[1]
θ1=acosψ,ψ=ω1t-φ
(21a)
幅—频关系
(21b)
KBM法第二次近似解[1]
(22a)
幅—频关系
(22b)
通常的振动问题按近似程度不同的工程要求可以分为:线性振动方程、弱非线性振动方程和强非线性振动方程.


图1 单摆运动分类Fig. 1 Classification of the pendulum motion
由上分析可知:单摆运动由线性变为非线性,其运动形态由单一的周期运动变为多样化的运动了.
2.2精确解
2.2.1单摆方程定性分析
(23)
哈密顿函数为(取最低点为零势能点)
(24)
其中h=const为积分常数.方程(23)就可写成
(25)
因此,非线性单摆系统(12)是一个保守系统或Hamilton系统.qn=nπ是系统的平衡点(n为整数).当n为偶数时,qn为椭圆型不动点坐标;当n为奇数时,qn为双曲型不动点坐标.从实际情况看,这样的平衡位置只有两个:一个是(0,0),中心点,若给它以微小的位移,单摆作周期振荡,平衡位置是稳定的,它是单摆下垂,摆球位于下方的位置.另一个是(±π,0),鞍点,若给它以微小的位移,单摆不再在平衡位置附近振荡,而是旋转起来,平衡位置是不稳定的,这是单摆摆球位于最上方的位置.

图2 单摆运动的相图Fig. 2 The phase diagram of the pendulum motion
2.2.2捕获轨道、非捕获轨道和界轨的解
为了给出单摆方程(12)一般相轨道的运动解,引进能量参数
(26)
显然,k<1对应于捕获轨道,k>1对应于非捕获轨道,k=1对应于界轨.
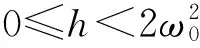
中心在(0,0),这是单摆振动的情况,设a是振幅,这时
(27)
而作用I的计算公式为
(28)
其中
(29)
引入变量α来代替q
(30)
表达式(28)可以改写成
(31)
其中K(k)和E(k)分别是第一类和第二类完全椭圆积分.
等式(31)确定了k的函数I.将它两边对k微分得
(32)

(33)
显然,哈密顿函数H只依赖于I,由(26)和(31)确定,得到
(34)
其中k=k(I)是I=I(k)的反函数,由(31)确定.
由(33)和(34)求得单摆振动角频率
(35)
单摆振动的周期
(36)
正则变换q,p→ψ,I的母函数,在变量替换(31)下为
(37)
其中F(α,k)和E(α,k)分别是第一类和第二类椭圆积分,α由等式(30)确定,而k=k(I)由(31)确定.角变量为
(38)
又由(30)得
(39)
由(37)得
(40)
考虑到(35)和(40),由公式(38)得出
(41)
由(29), (30)和(41)可得单摆振动情况下引入作用—角变量的正则变换
(42a)
(42b)
其中sn()和cn()分别为Jacobi椭圆正弦和余弦函数,且方程(12)的精确周期解为
(43)
将式(36)与线性单摆运动的周期式(14)比较有
(44)
将精确解(43)的右端[冯·卡门(Karman T V,1881~1963)]展开成Fourier级数,可得
(45)
其中
(46)

这是单摆旋转的情况,方程(12)的精确解为
(47)
单摆旋转的周期
(48)

这是单摆的同宿轨道.方程(12)的精确解为
(49)
2.3谐波-能量平衡法解
考察方程(16),设两项谐波解为
θ=a1cos(ωt)+a3cos(3ωt)
(50)
令ψ=ωt用Ritz平均法:
(51)
① 单项谐波解幅—频关系为
(52a)
初始条件的约束方程为:
(52b)
由(52)联立可解得ω,a1.
② 两项谐波解幅—频关系
(53a)
(53b)
初始条件的约束方程为:
(53c)
由(53)联立可解得ω,a1,a3.
2.4数值结果
图3给出了谐波-能量平衡法与精确解周期随振幅变化的关系T/T0~θmax的对比.

图3 周期变化关系(°°°本法;——精确解)Fig. 3 Period-amplitude relationship(°°°:the present method's results; —— :the exact results)
表1给出了谐波能量平衡法与其它方法的数值结果的比较.单项谐波法、两项谐波法和精确解的振幅完全相同θmax=a,KBM渐近法对方程(22)的二次近似解振幅为θmax2,Karman对精确解的两项级数展开法(45)振幅为θmaxii.

表1 谐波-能量平衡法与其它方法的数值结果比较

图4 相图a=π/3(°°°本法,——精确解)Fig. 4 Phase diagram a=π/3(°°°:the present method's results; —— :the exact results)

图5 相图a=π/2(°°°本法,——精确解)Fig. 5 phase diagram a=π/2(°°°:the present method's results; —— :the exact results)

图6 相图a=2π/3(°°°本法,——精确解)Fig. 6 Phase diagram a=2π/3(°°°:the present method's results; —— :the exact results)
图4~图9分别给出了a=π/3,a=π/2,a=2π/3,a=5π/6,a=2.8和a=3时单项谐波法、两项谐波法与精确解的相图比较.
以a=2.8为例,精确解为:

单项谐波能量平衡法解:
θ=2.8cos(0.54097ω0t),
两项谐波能量平衡法解:
θ=3.0236cos(0.52058ω0t)-
0.22361cos(1.5617ω0t),
KBM渐近法二阶近似解:
θ=2.8cos(0.5699ω0t)-0.242cos(1.7097ω0t),
Karman级数展开法二项近似解:
θ=3.0246cos(0.5610ω0t)-
0.25231cos(1.6830ω0t)
将近似解与精确解按角频率比较,可知当a在160°附近时,单项谐波解与精确解的误差为9.320%,两项谐波解与精确解的误差为5.200%,KBM法第二次近似解与精确解的误差为15.17%,Karman法二项近似解与精确解的误差为13.37%.

图7 相图a=5π/6(°°°本法,——精确解)Fig. 7 Phase diagram a=5π/6(°°°:the present method's results; —— :the exact results)
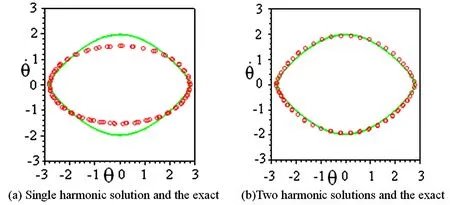
图8 相图a=2.8(°°°本法,——精确解)Fig. 8 Phase diagram a=2.8(°°°:the present method's results; —— :the exact results)

图9 相图a=3(°°°本法,——精确解)Fig. 9 Phase diagram a=3(°°°:the present method's results; —— :the exact results)
3 结论
1)本文应用谐波-能量平衡法求解了强非线性单摆问题,分别给出了单项谐波解和两项谐波解与精确解的比较.由图4~图9可见,当a>57°时,属于强非线性,单项谐波解与精确解定性拓扑一致,而两项谐波解与精确解相当一致.这表明谐波-能量平衡法既简单,又精确.
2)表1给出了谐波-能量平衡法、KBM渐近法、Karman级数展开法和精确解的比较,结果表明,对a≤57°的弱非线性情况,KBM渐近法、Karman级数展开法可以得到很好的结果.对a>57°的强非线性情况,KBM渐近法、Karman级数展开法与精确解的偏离都比较大,而两项谐波解与精确解相当一致.这表明谐波-能量平衡法对强非线性系统可以得到很高的精度.
3)谐波-能量平衡法引入了能量平衡得出的初始条件约束方程,仅用两项谐波就可得到较高的精度.克服了传统的谐波平衡法需要取比较多的谐波数量才能得到较高精度的缺点.
4)谐波-能量平衡法考虑了非线性等效特征.克服了传统的等效线性化方法精度较差的缺点.
1陈予恕.非线性振动.北京:高等教育出版社,2002 (Chen Y S. Nonlinear Vibration. Beijing: Higher education press, 2002 (in Chinese))
2Nayfeh A H, Mook D T. Nonlinear oscillations. New York: Wiley 1979
3戴世强,庄峰青.一类非线性振动系统的渐近解.中国科学A辑,1986,29(1):34~40 (Dai S Q, Zhuang F Q. Asymptotic solution for a class of nonlinear oscillatory systems.TheScienceofChinaA, 1986,29(1):34~40 (in Chinese))
4李骊.强非线性振动系统的定性理论与定量方法.北京:科学出版社,1997 (Li L. Qualitative theory and quantitative method for strongly nonlinear vibration system. Beijing:Science Press, 1997 (in Chinese))
5陈树辉,刘世龄,张佑启,徐兆.强非线性振动的定量方法.广州:广东科技出版社,1997 (Chen S H, Liu S L, Zhang Y Q, Xu Z. Quantitative method for strong nonlinear vibration. Guangzhou: Guangdong Science and Technology Press, 1997 (in Chinese))
6李银山,郝黎明,树学锋.强非线性Duffing方程的摄动解.太原理工大学学报,2000,31(5):516~520 (Li Y S, Hao L M, Shu X F. Asymptotic solution of strongly nonlinear Duffing equation.JournalofTaiyuanUniversityofTechnology, 2000,31(5):516~520 (in Chinese))
7Leung A Y T,Zhang Q C. Complex normal form for strongly nonlinear vibration systems exemplified by Duffing-van der Pol equation.JournalofSoundandVibration,1998,213(5):907~914
8李银山,李欣业,刘波.分岔混沌非线性振动及其在工程中的应用.河北工业大学学报,2004,32(3):80~83 (Li Y S, Li X Y, Liu B. Bifurcation chaos nonlinear oscillations and their application in engineer.JournalofHebeiUniversityofTechnology, 2004,32(2):96~103 (in Chinese))
9李银山,陈予恕,吴志强.正交各向异性圆板非线性振动的亚谐分岔.机械强度, 2001,23(2):148~151 (Li Y S, Chen Y S, Wu Z Q. Subharmonic bifurcation of nonlinear vibration of orthotropic circular plates.JournalofMechanicalStrength, 2001,23(2):148~151 (in Chinese))

11Li Y S, Zhang N M,Yang G T. 1/3 Subharmonic solution of elliptical sandwich plates.AppliedMathematicsandMechanics, 2003,24(10):1147~1157
12李银山,张善元,张明路等.材料非线性圆板的1/2⨁1/4亚谐解.振动与冲击,2006,25(3):115~120 (Li Y S, Zhang S Y, Zhang M L. 1/2+1/4 Subharmonic solution of a circular plate from nonlinear of material.JournalofVibrationandShock, 2006,25(3):115~120 (in Chinese))
13李银山,张善元,董青田,曹俊灵.用两项谐波法求解强非线性Duffing方程.太原理工大学学报,2005,36(6):690~693 (Li Y S, Zhang S Y, Dong Q T, Cao J L. Two harmonics method for strongly nonlinear Duffing equation.JounalofTaiyuanUniversityofTechnology, 2005,36(6):690~693 (in Chinese))
14李银山,张善元,李欣业,罗利军.强非线性动力系统的两项谐波法.太原理工大学学报, 2005,36(6):694~696 (Li YS, Zhang S Y, Li X Y, Luo L J. Two-harmonic method for strongly nonlinear dynamic systems.JournalofTaiyuanUniversityofTechnology, 2005,36(6):694~696 (in Chinese))
15李银山,张善元,刘波等.各种板边条件下大挠度圆板自由振动的分岔解.机械强度, 2007,29(1):30~353 (Li Y S, Zhang S Y, Liu B. Bifurcate solutions of free vibration of a circular plate under various boundary conditions.JournalofMechanicalStrength, 2007,29(1):30~35 (in Chinese))
16李银山,潘文波,吴艳艳,李欣业.非对称强非线性振动特征分析.动力学与控制学报,2012,10(1):15~20 (Li Y S, Pan W B, Wu Y Y, Li X Y. Asymmetric strongly nonlinear oscillation characteristic analysis.JournalofDynamicsandControl, 2012,10(1):15~20 (in Chinese))
*The project supported by the National Natural Science Foundation of China(10872063).
† Corresponding author E-mail: liyinshan@eyou.com
01 May 2015,revised 08 June 2015.
HARMONIC-ENERGY BALANCE METHOD FOR SOLVING PENDULUM EQUATION†
Li Yinshan1†Li Tong2Wei Bingwei1Li Xinye1
(1.DepartmentofMechanics,CollegeofMechanicalEng.,HebeiUniversityofTechnology,Tianjin300130China)(2.KeyLaboratoryofPressureSystemsandSafety,MinistryofEducation,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)
A harmonic-energy balance method is put forward to solve the strong nonlinear pendulum equation. The difference from the classical perturbation method is that the harmonic balance method does not account the differential equation and initial conditions separately, but it considers both simultaneously. Through the harmonic-balance method, two-order ordinary differential equations describing dynamic systems become a set of nonlinear algebraic equations with the variables of angular frequency and amplitude. Considering the balance of energy, the close equations with angular frequency and amplitude as the variables can be solved. The harmonic-energy balance method is a combination of harmonic-balance and energy balance. It overcomes the shortcomings of both methods and takes their advantages. A case study also shows that the harmonic-energy balance method is simpler with higher precision although it takes less harmonics.
strong nonlinear,pendulum,harmonic-energy balance method
E-mail: liyinshan@eyou.com
10.6052/1672-6553-2015-047
2015-05-01收到第1稿,2015-06-08收到修改稿.
*国家自然科学基金资助项目(10872063)
