微型Mindlin板非线性动力学模型的建立†

赵猛　陈丽华*　张伟

(1.北京工业大学机电学院, 北京　100124) (2.机械结构非线性振动与强度北京市重点实验室, 北京　100124)



微型Mindlin板非线性动力学模型的建立†

赵猛1,2陈丽华1,2*张伟1,2

(1.北京工业大学机电学院, 北京100124) (2.机械结构非线性振动与强度北京市重点实验室, 北京100124)

随着MEMS技术工艺的发展,微型结构在工程领域的应用越来越广泛.对于微型结构,经典连续介质力学理论的本构关系中不包含任何特征长度尺度,不能反映结构在微米尺度下的尺寸效应.本文基于Von Karman大变形理论和一阶剪切变形理论,把考虑尺寸效应的应变梯度理论推广至微型Mindlin板的非线性问题.分别计算微结构的应变能,包括宏观变形应变能和微观变形应变能两部分,结合微型Mindlin板结构的动能及外力功,代入Hamilton原理,得到了微型Mindlin板在大变形情况下的非线性动力学方程及边界条件.

非线性,Mindlin板,应变梯度,尺度效应,Hamilton原理

引言

近些年,微机电系统(MEMS)的迅速发展,使得整个业界都呈现出了微型化的特点,此类结构的尺寸都非常小,而实验结果表明:在微尺度下,结构会出现明显的尺度效应.然而由于经典连续介质力学理论中并不包含特征长度参数,因此并不能预测在微尺度下板结构所表现出来的尺度效应.

从Cosserat兄弟提出偶应力理论开始,许多学者针对微结构的尺度效应提出了一系列的理论,1964年,Mindlin[1]给出了弹性全应变梯度理论,除了通常的两个拉梅常数以外,还引入五个新的材料常数;1992年,Aifantis和Altan在本构方程中引入了应变张量的二阶梯度,提出了一种梯度弹性理论.1992年,Aifantis[2]构建了一种简单的应变梯度理论,采用了经典线性各向同性弹性理论所采用的拉梅常数;该理论中只使用了一个长度尺度参数.2003年,Lam[3]等引入了相同的高阶平衡约束,提出了一种有三个额外材料参数的弹性应变梯度理论.

与此同时,许多学者利用应变梯度理论对微型结构进行了研究,2008年,Papargyri-Beskou和Beskos[4]运用应变梯度理论分析了弹性梯度弯曲Kirchhoff微型板结构的静态变形、稳定性和线性固有频率;2010年,Papargyri-Beskou[5]等用他们以前得到的基本方程分析了固定和简支圆形弹性梯度薄板的静态变形;2011年,Wang[6]等基于Lam等提出的弹性应变梯度理论提出了一种线性Kirchhoff微型板结构模型,并研究了该结构的静态变形、固有频率和屈曲;2012年,Ramezani[7]提出了基于标准弹性应变梯度理论的一阶剪切变形微型板结构模型,主要研究了结构的静态弯曲和线性固有频率;2014年,Li[8]对基于应变梯度理论的双层简支Kirchhoff微型板进行了研究,得出尺寸效应对板的偏转、轴向应力以及零应力面的位置有较大的影响.

以上各位学者针对微型结构进行的是线性研究,而在大变形非线性研究方面:2004年,Lazopoulos[9]基于Aifantis提出的弹性应变梯度理论,结合von Karman几何非线性建立了Kirchhoff微型板结构的方程;2011年,Reddy[10]研究了微结构Euler-Bernoulli和Timoshenko功能梯度材料梁的非线性振动问题;2012年和2013年,Ramezani和Rajabi[11]利用应变梯度理论研究了微型梁结构的非线性问题,并发现非线性是提升结构固有频率的主要原因,但在某些特殊的长厚比情况下,尺度效应也有明显提升固有频率的效果.2013年,Ramezani[12]基于应变梯度理论对微型薄板结构进行了非线性振动的研究.

综上所述,针对微型结构的线性问题已进行了深入的研究,而应用应变梯度理论进行非线性研究工作目前还主要集中在梁结构和薄板结构,所以本文针对微型Mindlin板,综合考虑一阶剪切变形、Von Karman大变形和尺寸效应的影响,把应变梯度理论推广到Mindlin板的非线性问题,分别计算微结构的势能,动能及外力功,代入Hamilton原理,得到了微型Mindlin板在大变形情况下的非线性动力学方程及边界条件,该方程及边界条件可应用于MEMS结构中微型Mindlin板结构,进行非线性动力学分析,同时也可应用于微型机械结构、微型太阳能帆板等微型Mindlin板结构的振动控制的研究.

1　应变梯度理论

应变梯度理论在本构关系中引入了材料的特征长度尺寸,并考虑了应变梯度高阶张量对应变能密度函数的影响,能够描述和解释微构件力学性能的尺寸效应现象.应变梯度理论建立了连续介质框架下考虑应变梯度影响的新的本构模型,成为刻划微米尺度效应的有力工具,也是联系经典力学与原子力学之间现实可行的桥梁,它们是一种广义连续介质力学理论.

应变梯度理论有三种形式:

Ⅰ型应变梯度ηijk=uk,ij;

Ⅱ型应变梯度ηijk=εjk,i;

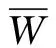
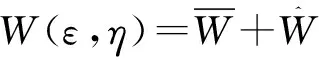
(1)

其中:

(2)

a4ηijkηijk+a5ηiikηkji

(3)

aJ(J=1,2,3,4,5)为材料的尺度参数.

根据(3)式可以得到高阶应力的表达式:

a2(ηpiiδqr+ηqiiδpr)+2a3ηiirδpq+

2a4ηpqr+a5(ηrqp+ηrpq)

(4)

δij为克罗内克函数.

2　模型的建立

针对微型Mindlin板,尺寸为a×b×h,

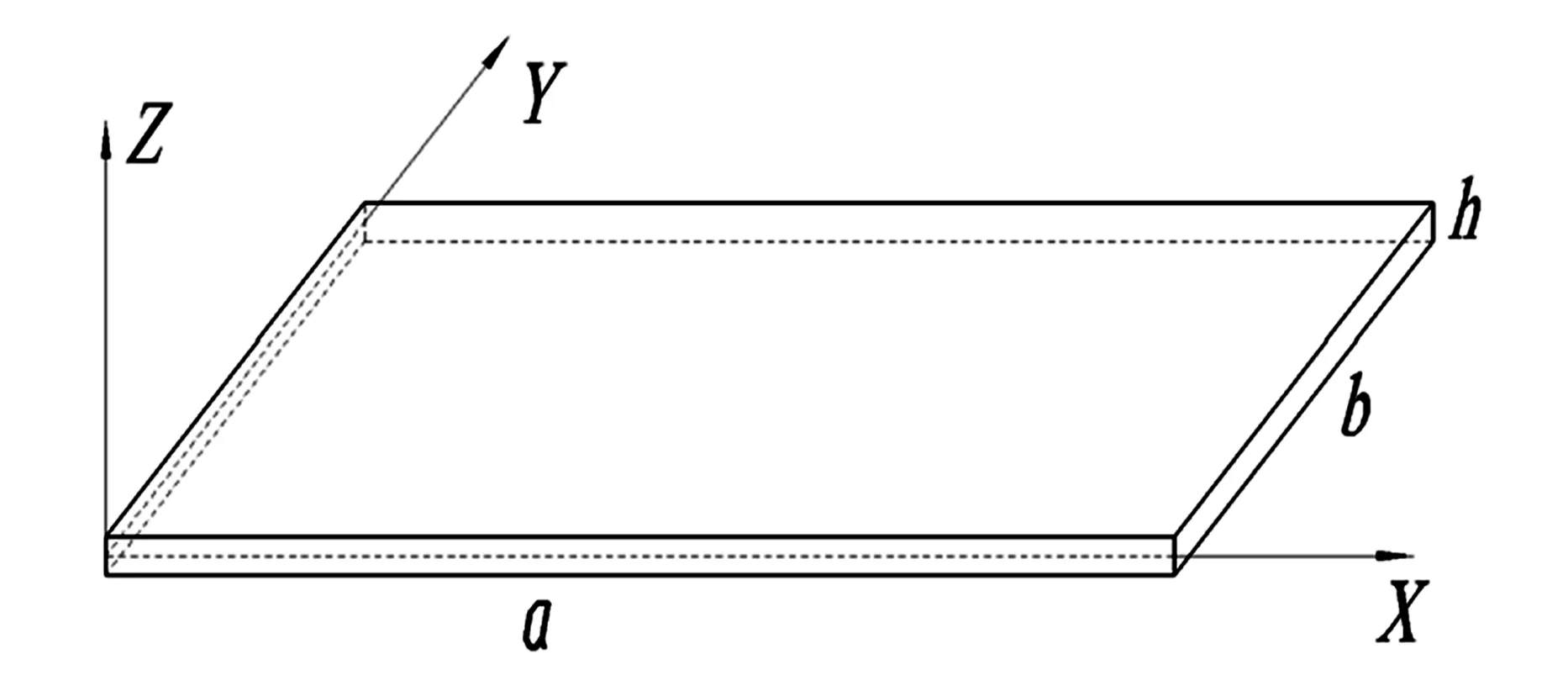
图1　结构示意图Fig. 1　The illustration of the Mindlin plate

综合考虑一阶剪切变形、VonKarman大变形和尺度效应的影响,利用Hamilton原理建立板结构的非线性动力学模型.

对于Mindlin板,板结构内任意一点沿X、Y、Z方向的位移分别为:

(5)

其中u0,v0,w0为中面上任意点在X、Y、Z方向的位移,φx,φy分别为绕Y轴和X轴的转角.

由VonKarman大变形理论,可以得到非线性应变表达式:

(6)

由本构关系得到应力表达式为:

(7)

E,υ分别为材料的弹性模量和泊松比.

设:

(8)

其中:h为板结构厚度.

基于经典连续介质力学,微型板结构宏观变形的应变能表达式为:

(9)

把由VonKarman大变形理论得到的非线性应变表达式(6)代入Ⅱ型应变梯度理论表达式ηijk=ηikj=εjk,i=εkj,i(i,j,k=x,y,z),得到非线性应变梯度表达式如下:

ηxzz=ηyzz=ηzzz=ηzxz=ηzzx=ηzyz=ηzzy=0

(10)

代入(4)式,得到非线性高阶应力表达式:

τxxx=2(a1+a2+a3+a4+a5)ηxxx+

(a1+2a2)ηxyy+(a1+2a3)ηyyx

τxxy=(a1+2a5)ηyxx+(a1+2a3)ηyyy+

2(a3+a4)ηxxy

τxyx=2(a4+a5)ηxxy

τxyy=(a1+2a2)ηxxx+(a1+2a5)ηyyx+

2(a2+a4)ηxyy

τxxz=(a1+2a5)ηzxx+2(a3+a4)ηxxz+

a1ηzyy+2a3ηyyz

τxzx=2(a4+a5)ηxxz

τxyz=2a4ηxyz+2a5ηzxy

τxzy=2a4ηxyz+2a5ηyxz

τxzz=(a1+2a2)ηxxx+a1ηyyx+2a2ηxyy

τyxx=(a1+2a5)ηxxy+(a1+2a2)ηyyy+

(2a2+2a4)ηyxx

τyzy=(2a4+2a5)ηyxy

τyyx=(a1+2a3)ηxxx+(a1+2a5)ηxyy+

(2a3+2a4)ηyyx

τyyy=(a1+2a3)ηxxy+(a1+2a2)ηyxx+

(2a1+2a2+2a3+2a4+2a5)ηyyy

τyxz=2a4ηyxz+2a5ηzxy

τyzx=2a4ηyxz+2a5ηxyz

τyyz=(a1+2a5)ηzyy+(2a3+2a4)ηyyz+

a1ηzxx+2a3ηxxz

τyzy=(2a4+2a5)ηyzy

τyzz=(a1+2a2)ηyyy+a1ηxxy+2a2ηyxx

τzxx=(a1+2a5)ηxxz+(2a2+2a4)ηzxx+

a1ηyyz+2a2ηzyy

τzxy=2a4ηzxy+2a5ηyxz

τzyx=2a4ηzxy+2a5ηxyz

τzyy=(a1+2a5)ηyyz+(2a2+2a4)ηzyy+

a1ηxxz+2a2ηzxx

τzzx=(a1+2a3)ηxxx+a1ηxyy+2a3ηyyx

τzzy=(a1+2a3)ηyyy+a1ηyxx+2a3ηxxy

τzzz=(a1+2a3)ηxxz+(a1+2a3)ηyyz+

(a1+2a2)ηzxx+(a1+2a2)ηzyy

τzxz=τzyz=0

(11)

同时设:

(12)

则微观变形部分的应变能为:

(13)

由此考虑尺度效应微型板结构的总应变能为:

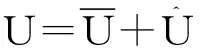
(14)

结构的动能和外力功分别为:

(15)

WE=∫Ω(qw)dxdy

(16)

其中:τijk为高阶应力,ηijk为高阶应变,ρ为材料密度,q(x,y)为结构所受横向分布力.

将(14)、(15)、(16)三式代入Hamilton原理:

(17)

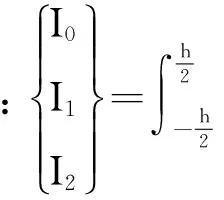
整理得到微型Mindlin板的非线性动力学方程:

(18)

(19)

(20)

(21)

(22)

同时得到了微型Mindlin板的边界条件:见表1、表2:

表1　x=0, a边界条件

表2　y=0, b边界条件

分别把(7)、(11)代入(8)和(12)式,再代入到动力学方程(18)～(22)和边界条件中,得到由位移表示的非线性动力学方程和边界条件.限于篇幅有限,本文并未列出.

3　结论

本文基于VonKarman大变形理论和一阶剪切变形理论,将应变梯度理论推广到Mindlin板的非线性问题,采用能够反映大变形的Ⅱ型应变梯度理论,分别计算微结构宏观变形的应变能和微观变形的应变能,结合微型Mindlin板结构的动能及外力功,基于Hamilton原理,得到了微型Mindlin板大变形情况下的非线性动力学方程及边界条件,方程和边界条件中分别包含宏观变形项和微观变形项,为MEMS结构中微型Mindlin板结构的非线性动力学分析提供了理论基础,同时方程可应用于微型机械结构、微型太阳能帆板等微型Mindlin板结构的振动控制的研究.

1MindlinRD.Micro-structureinlinearelasticity. Archive for Rational Mechanics and Analysis, 1964,16(1):51～78

2AifantisEC.Ontheroleofgradientsinthelocalizationofdeformationandfracture. International Journal of Engineering Science, 1992,30(10):1279～1299

3LamDCC,YangF,ChongACM,WangJ,TongP.Experimentsandtheoryinstraingradientelasticity. Journal of the Mechanics and Physics of Solids, 2003,51(8):1477～1508

4Papargyri-BeskouS,BeskosDE.Static,stabilityanddynamicanalysisofgradientelasticflexuralKirchhoffplates. Archive of Applied Mechanics, 2008,78(8):625～635

5Papargyri-BeskouS,GiannakopoulosAE,BeskosDE.Variationalanalysisofgradientelasticflexuralplatesunderstaticloading. International Journal of Solids Structures, 2010,47(20):2755～2766

6WangB,ZhouS,ZhaoJ,ChenX.Asize-dependentKirchhoffmicro-platemodelbasedonstraingradientelasticitytheory. European Journal of Mechanics A-Solids, 2011,30(4):517～524

7RamezaniS.Asheardeformationmicro-platemodelbasedonthemostgeneralformofstraingradientelasticity. International Journal of Mechanical Sciences, 2012,57(1):34～42

8LiAQ,ZhouSJ,ZhouSS,WangBL.Asize-dependentmodelforbi-layeredKirchhoffmicro-platebasedonstraingradientelasticitytheory. Composite Structures, 2014,113:272～280

9LazopoulosKA.Onthegradientstrainelasticitytheoryofplates. European Journal of Mechanics A-Solids, 2004,23(5):843～852

10ReddyJN.Microstructure-dependentcouplestresstheoriesoffunctionallygradedbeams. Journal of the Mechanics and Physics of Solids, 2011,59(11):2382～2399

11RajabiF,RamezaniS.Anonlinearmicrobeammodelbasedonstraingradientelasticitytheory. Acta Mechanica Solida Sinica, 2013,26(1):21～34

12RamezaniS.Nonlinearvibrationanalysisofmicro-platesbasedonstraingradientelasticitytheory. Nonlinear Dynamics, 2013,73(3):1399～1421

*TheprojectsupportedbytheNationalNaturalScienceFoundationofChina(11472019).

†CorrespondingauthorE-mail:chenlihua@bjut.edu.cn

09June2015,revised08July2015.

NONLINEARDYNAMICSMODELOFTHEMICRO-MINDLINPLATEBASEDONTHESTRAINGRADIENTTHEORY†

ZhaoMengChenLihua†ZhangWei

(Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures College of Mechanical Engineering,Beijing University of Technology, Beijing100124, China)

WiththedevelopmentofMEMSfabricatingtechnology,MEMSstructurenowhasawideapplicationinmanufacturingindustry.Meanwhile,becauseofnoanycharacteristiclengthscaleparametersinconstitutiverelationship,theclassicaltheoryofcontinuummechanicsisunlikelytopredictthesizeeffectundermicroscale.ThispaperinvestigatesthenonlinearproblemsofmicroMindlinplatesbasedonthefirst-ordersheardeformationtheoryandvonKarmannon-linearity,andthestraingradienttheoryisalsoutilizedtotakesizeeffectintoconsideration.NonlineardynamicmodelofthemicroMindlinplatealongwithitsboundaryconditionsareobtainedbytakingstrainenergy,includingstrainenergyofbothmacroandmicrodeformation,kineticenergyandexternalworkintoHamilton′sprinciple.

nonlinear,Mindlinplate,straingradienttheory,sizeeffect,Hamiltonprinciple

E-mail: chenlihua@bjut.edu.cn

10.6052/1672-6553-2015-078

2015-06-09收到第1稿,2015-07-08收到修改稿.

*国家自然科学基金资助项目(11472019)