一类随机Harrison型捕食与被捕食系统的稳定性分析†
2016-10-17牛嗣永靳艳飞
牛嗣永 靳艳飞
(北京理工大学 宇航学院力学系, 北京 100081)
一类随机Harrison型捕食与被捕食系统的稳定性分析†
牛嗣永靳艳飞†
(北京理工大学 宇航学院力学系, 北京100081)
研究了一种具有Harrison功能反应函数的随机捕食与被捕食系统模型,该模型中捕食者的死亡率和被捕食者的增长率受到独立同分布的两对称三值噪声的影响.文中运用线性化理论和Shapiro-Loginov方程给出了系统扰动的一阶矩和二阶矩方程,并用Routh-Hurwitz稳定性判据给出了系统稳定的条件.研究表明噪声强度σ和噪声自相关时间τ均对系统的稳定性有影响.当噪声强度充分大或噪声自相关时间足够小都能使系统失稳.最后通过数值方法,验证了分析结果的准确性.
三值噪声,Harrison捕食与被捕食系统,稳定性,矩方程,Shapiro-Loginov方程
引言
近年来在种群生态系统研究中,学者们已经建立了多种多样的生物模型[1-6],并对它们的动力学特性进行了深入的分析.然而这些模型大多是确定性模型,对于随机模型的研究还比较少[7-12].虽然很多情况下忽略环境的干扰,使用确定性模型就能得到种群变动的本质属性,但当环境扰动很强时,忽略随机因素会使分析结果产生较大偏差.人们一般将环境扰动以噪声的形式表示,如白噪声、色噪声等.May[10]指出由于环境噪声的存在,模型的出生率,承载能力,竞争参数及其它参数都或多或少的呈现波动现象.Mao[11]指出噪声不仅能减弱稳定性,还能增强稳定性.Qiu和liu[12]证明了白噪声激励下的B-D模型,对任意初始状态都存在唯一的正平衡解.然而在随机捕食与被捕食模型的研究中,大多仅考虑环境噪声为白噪声或色噪声时随机模型的动力学.相对于自然环境的多样性,这显然是不够的.本文采用三值噪声来描述自然环境的随机涨落现象.三值噪声是一种随机电报噪声,是真实噪声的典型模型.它在一定条件下能转变为高斯白噪声[13-15],因而能更好的描绘自然界中的环境波动.本文研究三值噪声激励下的Harrison捕食与被捕食系统模型,分析了噪声强度及噪声自相关时间对模型稳定性的影响.
一般确定性Harrison模型表达式如下:
(1)
其中,x和y分别表示被捕食者种群和捕食者种群的密度;r1表示被捕食者的自然增长率;r1/α表示环境容纳量;c、m和μ分别表示半饱和常数、捕食者的捕获率和转化率;r2表示捕食者的自然死亡率.
1 模型建立
考虑环境对种群出生率和死亡率影响较大,将环境噪声分别作用于被捕食者种群的增长率和捕食者种群的死亡率上,即确定性模型(1)中参数r1和r2作如下变换:
r1→r1+ε1(t), -r2→-r2+ε2(t)
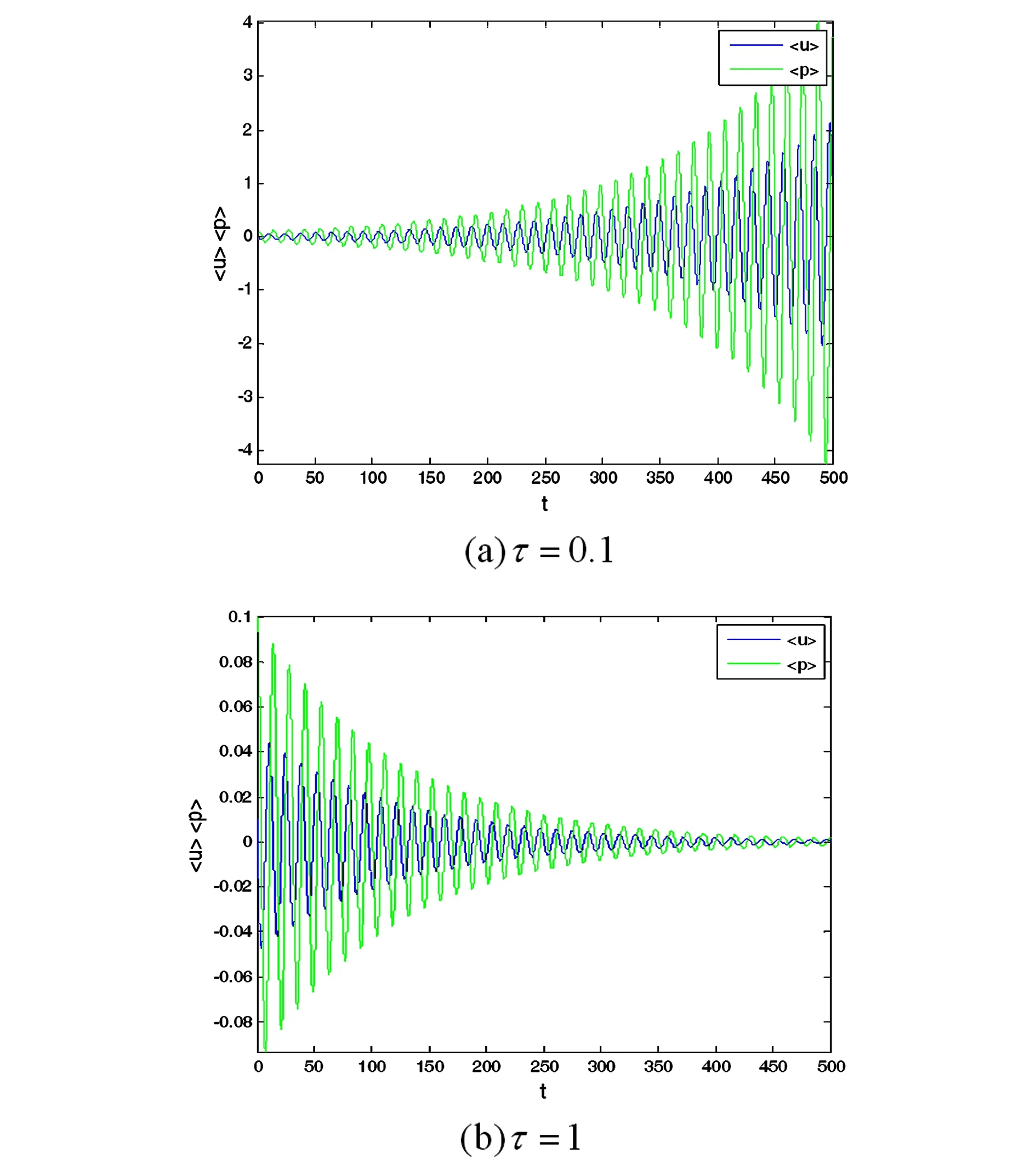
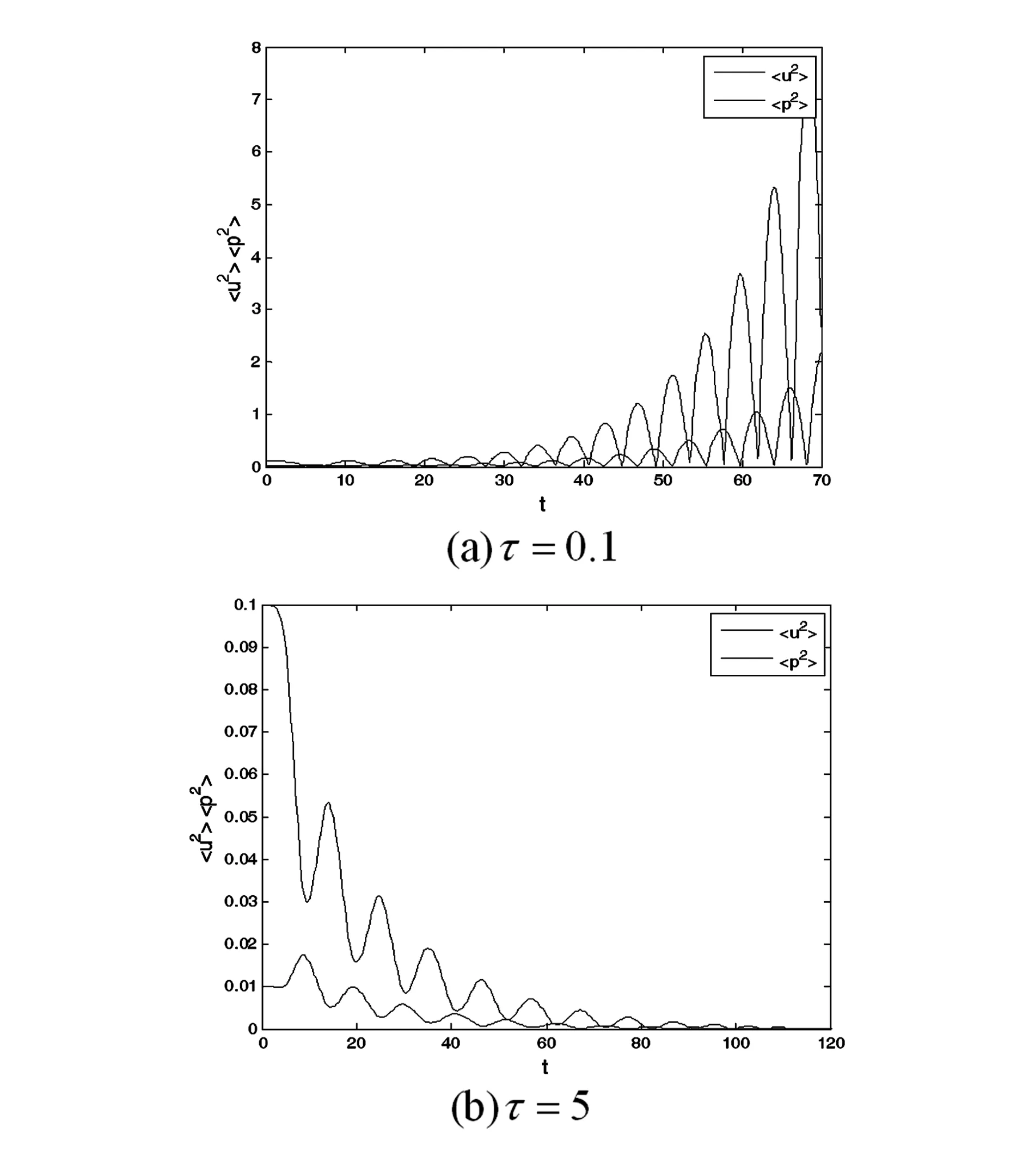
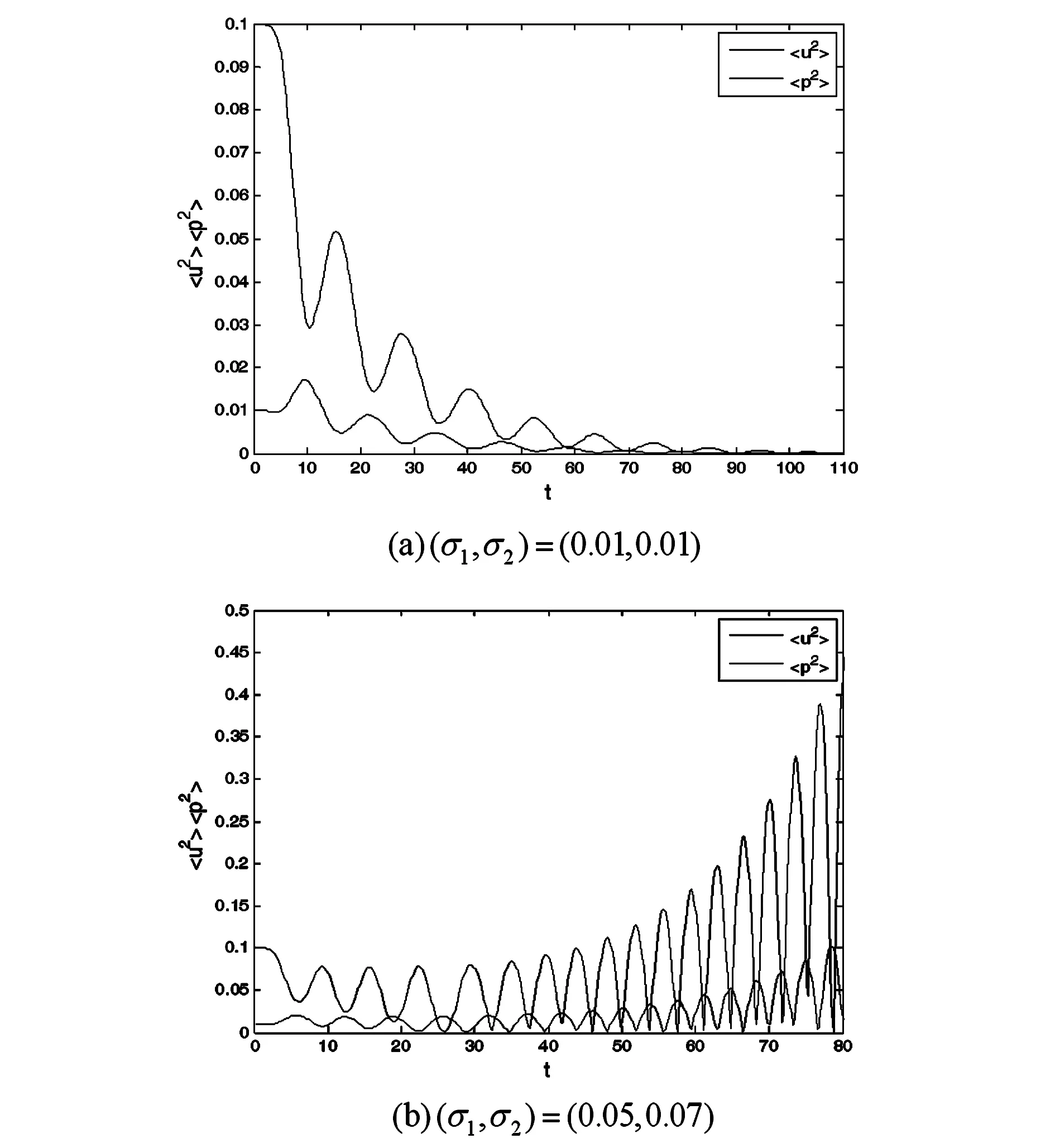
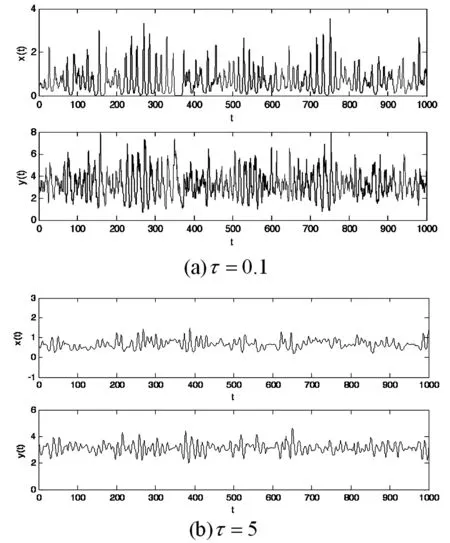
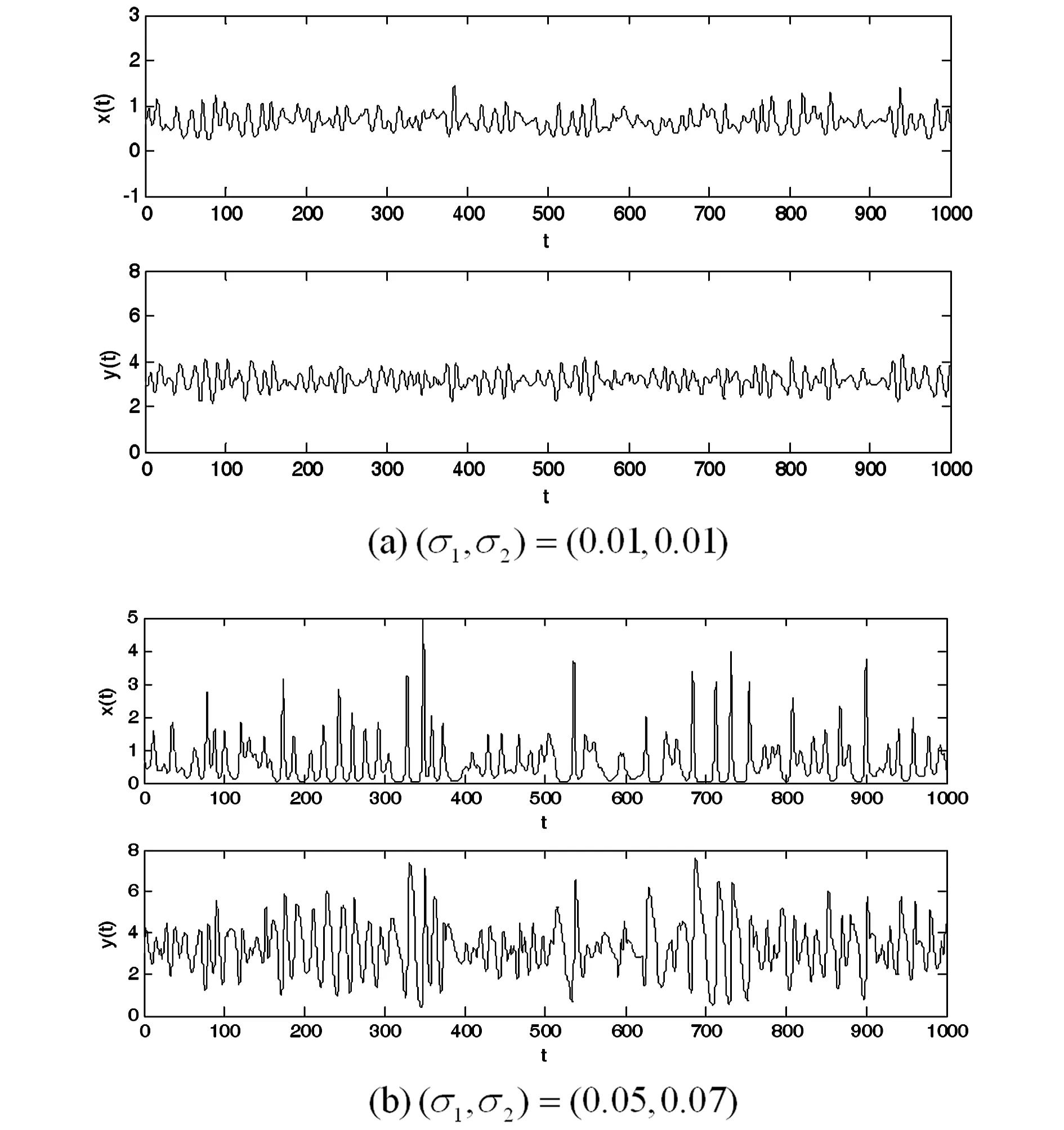
式中,εi(t)(i=1,2)表示相互独立的对称三值噪声.噪声在3个值a,0,-a之间发生跃迁,稳态概率满足Ps(a)=Ps(-a)=q,Ps(0)=1-2q(0 〈εi(t)εj(t)〉=0 (i,j=1,2 i≠j) 其中λ表示跃迁概率,是噪声自自相关时间τ的倒数,即,λ=1/τ,噪声强度σ=4qa2/λ. 相应的随机模型表示为: (2) 显然,确定性Harrison模型(1)存在如下三个平衡点: E1=(0,0), E2=(r1/α,0), E†=(x†,y†) 其中 这里只有E†是两种群共存的平衡点.下文将研究噪声对模型处于正平衡点E†状态时稳定性的影响. 本节分为两部分研究对称三值噪声激励下随机模型(2)的稳定性.我们分别通过对其线性系统一阶矩和二阶矩的稳定性分析,给出其一阶矩和二阶矩稳定的条件.在每部分都有相应的数值模拟来验证分析结果. 2.1一阶矩 在随机系统中引入小扰动(u,p),令x=x†+u,y=y†+p,代入系统(2)并线性化可得: (3) 其中: 对系统(3)取数学期望,可得到关于u,p一阶矩的微分方程如下: (4) (5) 运用Shapiro-Loginov方程[16],可得: (6) 系统(3)第一行乘以ε1(t)后取数学期望,然后将式(6)代入可得: (7) 同样方法可得: (8) (9) (10) 式(4)~(5)和(7)~(10)一起写为下面的线性微分方程组: (11) 线性系统(11)的特征方程为: a0r6+a1r5+a2r4+a3r3+a4r2+a5r+a6=0 (12) 式中: a0=1,a1=4λ- 3f1- 3f4 a2=3(f1+f4)2-10λ(f1+f4)+3f1f4-3f2f3- λ(σ1+σ2)+6λ2 f1f4-2λ2)+σ1λ(f1+3f4)+σ2λ(3f1+ f4)-8λ(f2f3-f1f4)-3λ2(σ1+σ2) a4=-2λ(f1+f4)3+(f1+f4)2(3f1f4+7λ2)- 6λ(f1+f4)(λ2+2f1f4+2f2f3)+3f12f42+ λf1f4[8λ-3(σ1+σ2)-12f2f3]+3f22f32+ f2f3[λ(σ1+σ2)+3(f12+f42)]+ λ2(σ1+σ2)(7f4-3λ) a5=-λ4(σ1+σ2+f1+f4)+λ3[2(f1+f4)2+ 4(f1f4-f2f3)+2σ1σ2+σ1f1+5σ2f1+5σ1f4+ σ2f4]-λ2[(f1+f4)3+8(f1+f4)(f1f4-f2f3)+ 5σ2f12+5σ1f42+σ1σ2(f1+f4)-f2f3(σ1+σ2)- 4f1f(σ1-σ2)]+λ{2(f1f4-f2f3)[(σ2f1+ σ1f4)+2(f1+f4)2]+(f1+f4)(σ2f12+σ1f42)+ 4(f1f4-f2f3)2-2f1f2f3f4}-3(f1+f4)(f1f4-f2f3) a6=λ4(f1f4-f2f3+σ1σ2+σ2f1+σ1f4)- λ3[σ2f1(f1+σ1)+σ1f4(f4+σ2)+ (f1+f4)(σ2f1+σ1f4+2f1f4-2f2f3)]+ λ2{(f1f4-f2f3)[(f1+f4)2+σ2f1+σ1f4]+ (f1f4-f2f3)2+(f1+f4)(σ2f12+σ1f42)+ σ1σ2f1f4}-λ{(f1f4-f2f3)(σ2f12+σ1f42)+ 2(f1+f4)(f1f4-f2f3)2]+(f1f4-f2f3)3 根据Routh-Hurwitz稳定性判据,可得系统(11)稳定的充分条件是: (13) 由条件(13)可给出一阶矩系统(11)的稳定区间.为简化计算我们取一组参数:r1=1.5,α=0.1,m=0.6,r2=0.2,μ=0.4,c=0.1(后面所绘图形所取参数与此相同,不再赘述).图1给出了确定性Harrison模型(1)关于种群x和y的时间历程图与相图,初值取为(x0,y0)=(4,0.5).可以看到此时确定性系统有一正平衡点E†=(0.657,3.14),且E†是渐近稳定的. 在图2(a)中,我们以噪声强度(σ1,σ2)为变量,固定其它参数,给出了一阶矩系统在(σ1,σ2)平面上的稳定区间.在图2(b)和图2(c)中,我们固定噪声自相关时间τ=0.2,给出了取不同噪声强度组合时一阶矩的时间历程图.可以看到,当噪声强度组合在图2(a)中斜线下方的稳定区间时,一阶矩随时间增长而趋于零,可以推断出此时一阶矩系统是稳定的(如图2(b)所示).当噪声强度组合落在不稳定区间时,一阶矩随着时间的推移,振幅逐渐变大(如图2(c)所示),即系统是不稳定的.接下来我们固定噪声强度,讨论了噪声自相关时间对一阶矩系统稳定性的影响.图3中我们固定噪声强度,给出了不同噪声自相关时间下,一阶矩的时间历程图.从图中可以看出,随着噪声自相关时间τ的增大,一阶矩系统变得稳定,即噪声的有色性能提高系统的稳定性. 图1 确定性Harrison模型Fig. 1 Deterministic Harrison model 图2 τ=0.2时噪声强度对一阶矩稳定性的影响 图3 噪声自相关时间对一阶矩稳定性的影响,取(σ1,σ2)=(0.07,0.06)Fig. 3 Effect of noise auto-correlation time of the first-order moments with (σ1,σ2)=(0.07,0.06) 2.2二阶矩 (14) 对公式(14)取数学期望,得到二阶矩方程: 同样方法,并运用Shapiro-Loginov方程可得下列各等式: 〈ε1up〉+〈ε2up〉 2f2〈ε1up〉 f2〈ε1p2〉+σ1λ〈up〉 f2〈ε2p2〉+σ2λ〈up〉 与一阶矩相同,将上述方程一起写为关于系统二阶矩的线性微分方程: (15) 式中, 线性微分方程(15)的特征方程为: b0r9+b1r8+b2r7+b3r6+b4r5+b5r4+b6r3+ b7r2+b8r+b9=0 其中, b0=1,b1=4λ-9(f1+f4), f4)+12(f1f4-f2f3)+6λ2 …… 由于bi(i=3,…,9)的表达式太长,本文没有给出. 由Routh-Hurwitz稳定性判据可知,二阶矩系统(15)稳定的充分条件是: (16) 上述行列式中,若j>9则取bj=0. 在图4中,固定噪声强度(σ1,σ2)=(0.02,0.02) 给出了不同噪声自相关时间下系统二阶矩的时间历程图.可以看到随着噪声自相关时间τ的增大,系统的稳定性增加.图5中,我们固定噪声自相关时间τ=3,给出了不同噪声强度时系统二阶矩的时间历程图.从图中可以看出随着噪声强度的增加,系统变得不稳定. 图4 不同噪声自相关时间时的系统二阶矩的时间历程图,取(σ1,σ2)=(0.02,0.02) 图5 不同噪声强度时的系统二阶矩的时间历程图,取τ=3Fig. 5 Time history of the second-order moments for auto-correlation time τ=3 and different noise intensities 下面通过数值方法呈现随机系统(2)的复杂动力学行为.在图6和图7中种群密度初值(x0,y0)取为靠近正平衡点的(0.6,3),其它参数的选取分别与二阶矩系统稳定性讨论中的图4和图5相同.图6给出了随机系统在不同噪声自相关时间的三值噪声作用下,种群密度(x,y)的时间历程图.可以看到当噪声自相关时间较大时(τ=5),两种群密度(x,y)在正平衡点附近的有限范围内波动,此时仍可视为系统稳定(如图6(b));而当τ减小到0.1时,种群密度(x,y)波动强烈,说明系统正平衡点E†变得不稳定(如图6(a)),系统失稳,这与二阶矩系统稳定性分析中图4的结果相同,即如果环境扰动的自相关时间较小,即使强度很小的外界扰动也可能导致随机捕食与被捕食系统失稳;而如果扰动的自相关时间较大,随机系统在相对较强的外界扰动下也能保持稳定,可以说系统的承受能力变强.总的来说就是,噪声的“有色性”能提高系统的稳定性.在图7中,固定噪声自相关时间τ=3,绘制了不同噪声强度组合下,随机系统种群密度(x,y)的时间历程图.当噪声强度取较小的(0.01,0.01)时,两种群密度(x,y)在平衡点附近小幅波动,没有改变系统的稳定性(如图7(a)所示);当噪声强度增大到(0.05,0.07)时,两种群密度波动剧烈,振荡幅值远离平衡点,系统变得不稳定(如图7(b)所示).这说明环境扰动强度越大,随机系统越可能失稳. 图6 不同噪声自相关时间时两种群密度的时间历程图,取(σ1,σ2)=(0.02,0.02)Fig. 6 Time histories of model (2) for noise intensities (σ1,σ2)=(0.02,0.02) and different correlation time 图7 不同噪声强度时两种群密度的时间历程图,取τ=3Fig. 7 Time histories of model (2) for correlation timeτ=3 and different noise intensities 本文研究了噪声强度和自相关时间对三值噪声激励的Harrison型捕食与被捕食系统稳定性的影响.运用线性化理论和Shapiro-Loginov公式推导出系统解的一阶矩和二阶矩方程,并给出了系统解矩的稳定性条件.研究表明:充分小的扰动并不能改变系统解的稳定性,当噪声强度σ较大时系统正平衡态可能发生失稳.即在较大的随机环境扰动下,物种共存态会被破坏.此外,当噪声强度不变,噪声自相关时间τ变得足够小时,系统也会失稳.说明相比于高斯白噪声,三值噪声的有色性能提高系统解的稳定性.最后通过数值方法验证了分析结果. 1Szabó G. Competing associations in six-species predator-prey models.JournalofPhysicsA:MathematicalandGeneral, 2005,38(30):6689~6702 2Sun X K, Huo H F, Zhang X B. A predator-prey model with functional response and stage structure for prey.AbstractandAppliedAnalysis, 2012,2012:1~19 3Morozov A, Petrovskii S, Li B L. Bifurcations and chaos in a predator-prey system with the Allee effect.ProceedingsBiologicalSciences/TheRoyalSociety,2004,271(1546):407~1414 4Shi R, Chen L. The study of a ratio-dependent predator-prey model with stage structure in the prey.NonlinearDynamics,2009,58(1-2):443~451 5Hwang T W. Global analysis of the predator-prey system with Beddington-DeAngelis functional response.JournalofMathematicalAnalysisandApplications, 2003,281(1):395~401 6陈方方, 洪灵. 一类具有时滞和非线性发生率的SIRS传染病模型稳定性. 动力学与控制学报, 2014,12(1):80~85 (Chen F F, Hong L. Stability and hopf bifurcation analysis of a delayed sirs epidemic model with nonlinear saturation incidence.JournalofDynamicsandControl, 2014,12(1):80~85 (in chinese)) 7Valenti D, Pizzolato N, Spagnolo B. Mean field approach and role of the coloured noise in the dynamics of three interacting species.ActaPhysicaPolonicaSeriesB, 2010,4123(87):5~45 8Zhong W R, Shao Y Z, He Z H. Correlated noises in a prey-predator ecosystem.ChinesePhysicsLetters, 2006,23(3):42~45 9Rao F. Dynamics of a delayed predator-prey model with stochastic perturbation.JournalofBiomathematics, 2011,26(4):609~624 10May R M. Stability and complexity in model ecosystems. New Jersey: Princeton University Press, 2001 11Mao X Y. Stochastic stabilization and destabilization.Systems&ControlLetters, 1994,23(4):279~290 12Qiu H, Liu M, Wang K, Wang Y. Dynamics of a stochastic predator-prey system with Beddington-DeAngelis functional response.AppliedMathematicsandComputation, 2012,219(4):2303~2312 13Mankin R, Ainsaar A, Haljas A, Reiter E. Trichotomous-noise-induced catastrophic shifts in symbiotic ecosystems.PhysicalReviewE, 2002,65(5):051108(1-9) 14Sancho J M. External dichotomous noise: The problem of the mean-first-passage time.PhysicalReviewA, 1985,31(5):3523~3525 15Schmid G J, Reimann P, Hänggi P. Control of reaction rate by asymmetric two-state noise.TheJournalofChemicalPhysics,1999,111(8):3349 16Shapiro V E, Loginov V M. Formulae of differentiation and their use for solving stochastic equations.PhysicaA, 1978,91(3-4):563~574 *The project supported by the National Natural Science Foundation of China (11272051) † Corresponding author E-mail: jinyf@bit.edu.cn 13 March 2015,revised 22 April 2015. STABILITY ANALYSISOF A STOCHASTIC PREDATOR-PREY MODEL WITH HARRISON FUNCTIONAL RESPONSE† Niu SiyongJin Yanfei† (DepartmentofMechanics,BeijingInstituteofTechnology,Beijing10081,China) The stability of a Harrison predator-prey model driven by symmetric trichotomous noises is studied in this paper. Using the Shapiro-Loginov formula, the first-order and second-order moments of the linearized system are obtained. Then, the stability condition of the Harrison predator-prey model is given by using Routh-Hurwitz stability criterion. It is found that the stability of the system depends on the noise intensities and correlation time. Finally, some numerical results are performed to support the theoretical analyses. trichotomous noise,Harrison predator-prey model,stability analysis,moment equations,Shapiro-Loginov formula E-mail:jinyf@bit.edu.cn 10.6052/1672-6553-2015-022 2015-03-13收到第1稿,2015-04-22收到修改稿. *国家自然科学基金资助项目(11272051)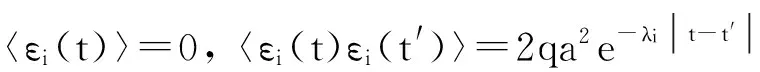
2 稳定性分析
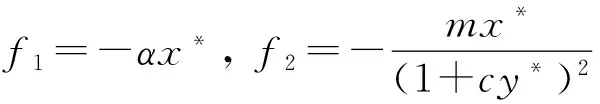
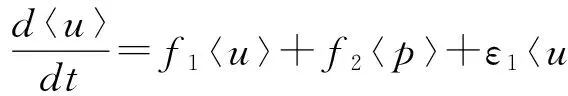
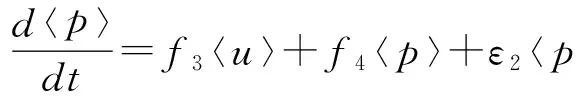
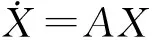
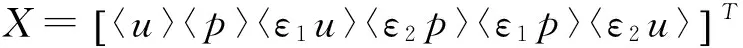
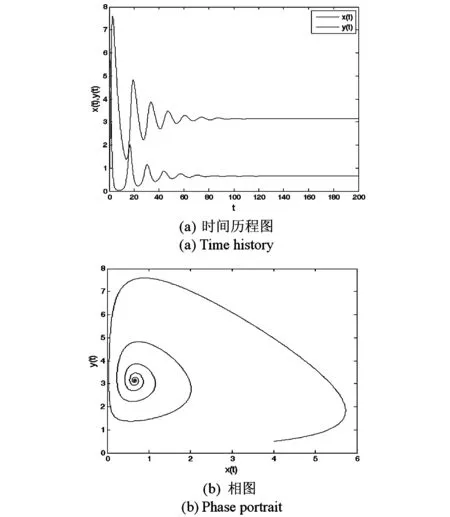
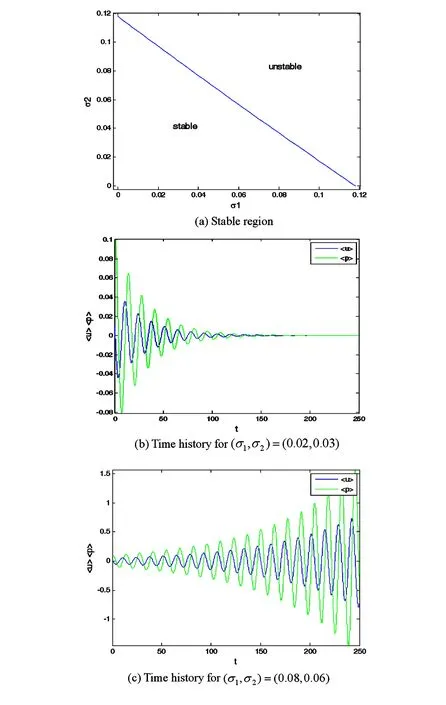
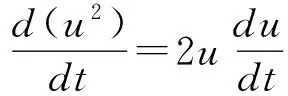
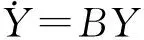
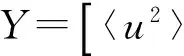
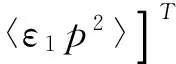

3 数值模拟
4 结论
