基于时频域交替法的迟滞非线性振动系统的稳态响应分析†

李东武　徐超

(西北工业大学航天学院, 西安　710072)



基于时频域交替法的迟滞非线性振动系统的稳态响应分析†

李东武徐超†

(西北工业大学航天学院, 西安710072)

连接界面的黏滑、摩擦行为不仅是引起结构刚度和阻尼非线性的主要原因,而且是结构无源阻尼的主要来源.Iwan模型能够较好地复现连接界面的黏滑、摩擦行为.本文采用时频域交替法(AlternatingFrequency/TimeDomainMethod,AFT)研究含Iwan非线性模型的单自由度振子系统的稳态响应.时频域交替法具有频域法求解线性系统响应的高效性和时域法判断非线性力的便捷性特点,采用离散傅里叶变换和傅里叶逆变换,在频域和时域内分别求解系统响应和对应的非线性恢复力,再反复迭代计算系统的稳态响应.将时频域交替法计算结果和中心差分法计算的结果进行对比,并研究激励幅值对系统非线性特征的影响.结果表明,时频域交替法计算的结果与中心差分计算的结果具有较好的一致性,且求解效率较高,计算耗时减少50%;随着激励幅值的增加,系统的能量耗散增加,刚度降低,固有频率降低.

连接,迟滞非线性,Iwan模型,时频域交替法,稳态响应

引言

航空、航天和机械等工程装备系统中的部件大多是通过螺栓、铆钉等连接装置装配而成.当连接结构受到外部周期载荷激励时,连接结合面间会发生摩擦、滑移和间隙等非线性行为,这些非线性行为不仅是引起结构振动能量耗散和阻尼衰减的主要原因,而且还造成了连接结构刚度和阻尼的非线性.连接面间的摩擦行为是一个非常复杂的物理现象,它是系统无源阻尼的主要来源[1].已有研究表明,在切向载荷作用下,连接界面的运动将经历从局部微观滑移到宏观相对运动的过程,切向恢复力与相对位移之间为非线性迟滞关系[2-3].为了描述界面的这种多尺度粘滑摩擦过程,国内外学者已提出一些唯象的迟滞非线性模型,例如,美国sandia国家实验室提出的四参数Iwan模型,德国斯图加特大学提出的Valanis模型以及微分形式的Bouc-Wen模型等[4-5].其中,Iwan模型形式简单,模型参数具有一定的物理意义,被认为是目前研究连接界面迟滞非线性粘滑摩擦行为的一种较好的模型.

Iwan迟滞非线性模型是一种不光滑模型,因此系统的动力学求解较为复杂.目前常用的求解非线性系统稳态响应的方法有两种：第一种是时域法,比如中心差分法、Runge-Kutta法等直接积分方法.直接积分法用有限元法离散空间变量,用有限差分法离散时间变量,它适合于任何情况.这类方法的优点是只要时间步长选择合适,计算结果会有很高的精度,而且可以运用于任意复杂的非线性系统;缺点是在速度转换点附近需要采用较小的步长以保证计算结果的精度,导致计算过程所需的时间较长.第二种是频域法,比如谐波平衡法[6].该方法先假设出系统响应的谐波解,再代入振动系统方程进行傅里叶级数展开求解未知参数来得到系统的稳态响应.这类方法的特点是：低阶谐波下计算效率较高但精度较差,随着谐波阶次的增加,计算精度变高但计算量迅速增大,计算效率降低.

时频交替法(AlternatingFrequency/TimeDomainMethod)是一种求解复杂非线性系统动力响应的新方法,其求解过程融合了频域中求解系统振动微分方程的高效性(使微分方程运算变为数值微分方程)和时域内判断非线性力的便捷性,并通过快速离散傅里叶正逆变换,将时域函数和频域函数进行转换,经过反复的迭代最终得到振动系统的稳态响应.本文采用时频域交替法来求解含Iwan非线性模型单自由度系统的稳态响应,首先给出了Iwan串-并联模型的非线性力表达式,推导了时频域交替法求解的具体公式和步骤,并对时频域交替法求解计算的收敛性和效率进行了分析研究.

1　Iwan迟滞非线性模型

图1所示为Iwan串-并联模型,它是由N个Jenkins单元并联而成,Jenkins单元则是由刚度为kn/N的线性弹簧和屈服力为fi†/N的阻尼滑块串联而成.在振动过程中,如果只有部分Jenkins单元发生滑移,则称模型发生了微滑移,微滑移现象普遍存在,它是结构无源阻尼的重要来源;如果所有Jenkins单元都发生滑移,则称模型发生了宏滑移.此时模型恢复力f 达到最大值fy(称为临界宏观滑移力).图2为Iwan模型微观滑动时的力-位移关系曲线(迟滞回线),包括初始加载段oa(又称骨干曲线)、卸载段abc和加载段cda.

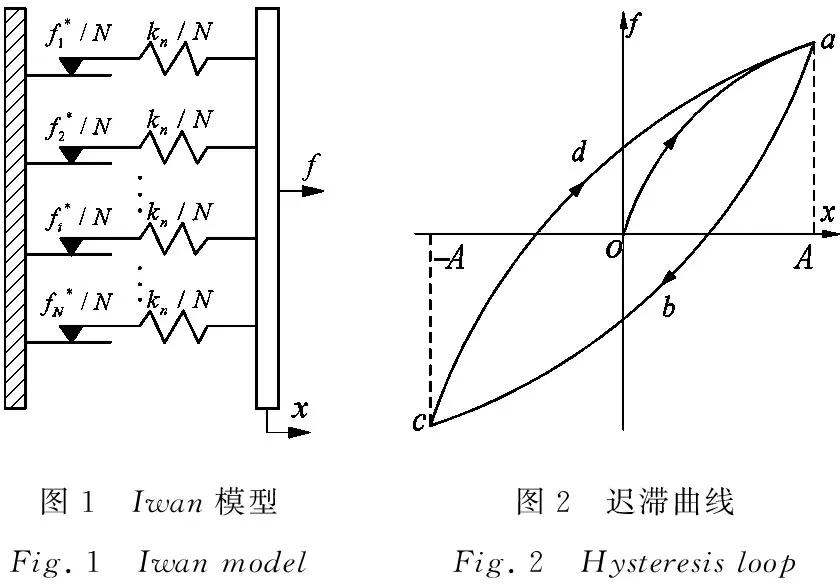
图1 Iwan模型Fig.1 Iwanmodel图2 迟滞曲线Fig.2 Hysteresisloop

本文选用连续Iwan模型作为研究对象,“连续”是指模型中Jenkins单元的数目N趋于无穷,采用概率密度函数φ(f†)来定义阻尼滑块的屈服力fi†.在螺栓连接模型中,结合面接触压强从螺栓连接处沿连接面展向呈线性单调递减,而且模型屈服力和接触压强具有相同的分布形式[7-8],因此,屈服力fi†(i=1,2,…)在[0,fN]区间内服从均匀分布.假设Iwan模型发生宏观滑移,则：

(1)

解得

fN=2fy

(2)

因此,根据均匀分布的定义可以得到屈服力的概率密度函数φ(f†)为

(3)

当Iwan模型受到外激励作用时,其恢复力为

(4)

将式(3)代入式(4)得到恢复力函数：

(5)

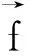
(6)

(7)

上式中左右箭头分别表示卸载和加载,A表示模型滑动的最大位移量.

从模型的力-位移关系曲线图2可以看出,Iwan模型的能量耗散为曲线所包络的面积, 下面根据系统的稳态响应,来推导单位周期内Iwan模型的能量耗散为：

(8)

将式(6)、(7)代入式(8)得微观黏滑下的能量耗散为：

(9)

同理可得宏观滑移下的能量耗散为：

(10)

2　时频域交替法

在结构动力学中,频域结果比时域结果包含更多的结构响应信息,在频域中求解线性系统可以有效避免卷积计算[10-11],因此频率法经常被用来求解动力学方程.通常情况下,非线性力是系统状态轨迹函数,它不是时间的显式函数,这就使得非线性力很难在频域内分析,但是它却容易在时域内计算获得.时频域交替法融合了时域法和频域法的优点,利用了频域法求解线性系统响应的高效性和时域法计算非线性力的便捷性,通过快速傅里叶变换(FFT)将非线性力的时域函数转换至频域,求解得到系统的频域稳态响应,再将频域响应通过傅里叶逆变换转换至时域,进而得到系统的非线性力时域函数,通过反复迭代最终得到系统的稳态解.在该方法计算时,需要将变量反复在时域和频域间相互转换.

图3所示为单自由度振子系统,其中m、k、c分别为系统振子质量、刚度、阻尼,f(t)为外激励,x(t)为振子的位移响应,Iwan代指图1所示的Iwan非线性模型.

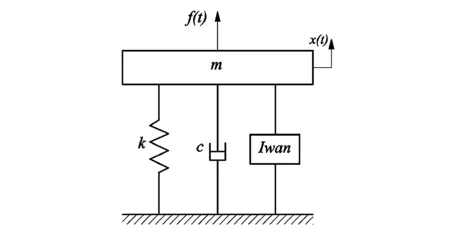
图3　含Iwan非线性模型的单自由度振子系统Fig. 3　Single DOF oscillator system with Iwan nonlinear model

图3所示单自由度系统的振动微分方程为：

(11)

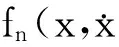
(12)

将其代入到式(11)得到频域内的振动方程：

(-mω2+jωc+k)·x(ω)=

f(ω)-fn(ω,x(ω))

(13)

其中ω是指由快速傅里叶变换引入的离散频率：

ω={ωk}

(14)

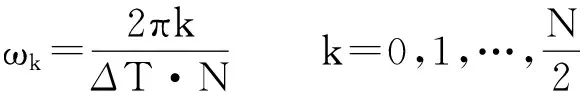
(15)

其中ΔT为采样周期,N为快速傅里叶变换中时域函数的样本数目,由于快速傅里叶变换后的频域值关于ωN/2对称,因此k的取值长度为N/2+1.

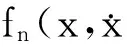
(-mω2+jωc+k)·xi(ω)=

f(ω)-fn(ω,xi-1(ω))

(16)

在这个过程中,初始位移响应和速度响应的获取方法是：忽略非线性力的影响,将系统看作简单的线性系统,通过时频域交替法求得系统的稳态响应.即

(-mω2+jωc+k)·x(ω)=f(ω)

(17)

算法计算过程如图4所示。

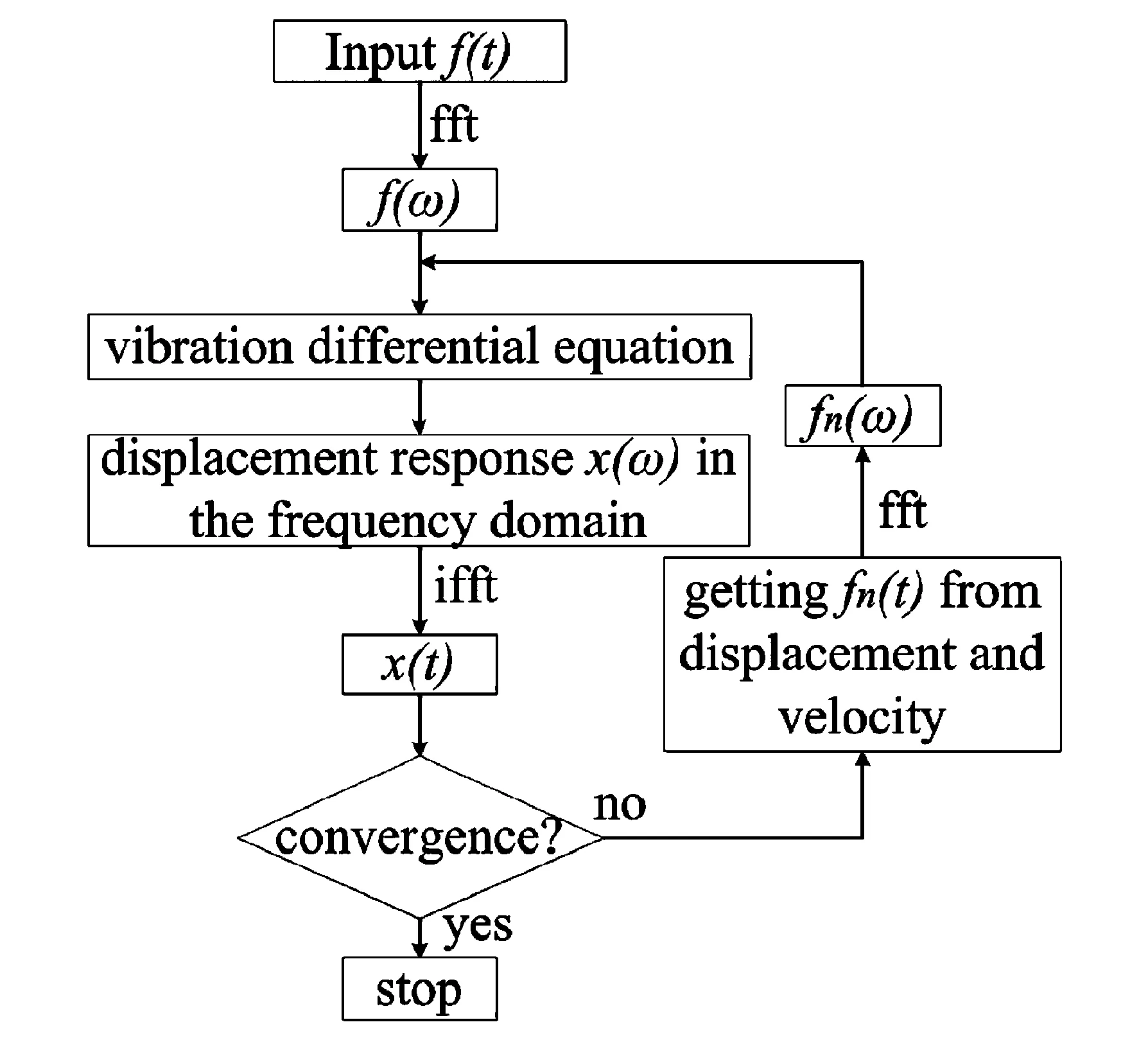
图4　时频域交替法计算的流程图Fig.4　Flow diagram of the calculation through AFT method

算法计算过程中的关键控制参数有采样频率、决定迭代收敛与否的控制参数,考虑到算法计算精度和计算效率的要求,本文选择采样频率为128Hz,也可选为256Hz;迭代收敛的控制参数由第4节详细介绍.

3　数值算例

考虑两种激励幅值下的系统响应,第一种情况：f(t)=1.5sin(3t),时频域交替法求解的结果如图5、图6所示 ：

图5　模型微滑时的稳态响应Fig. 5　Steady-state response in microslip

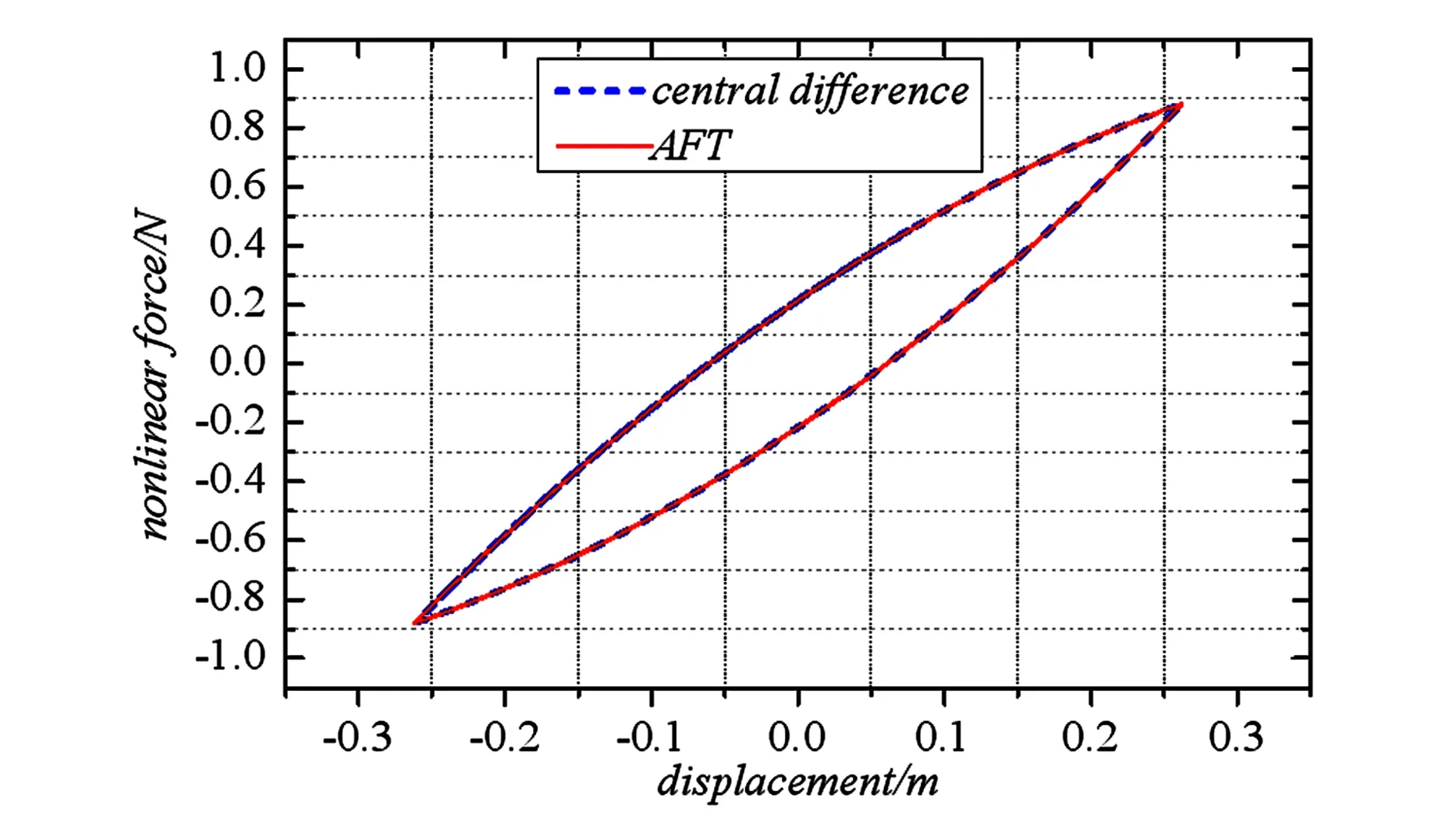
图6　模型微滑时的迟滞曲线Fig. 6　Hysteresis loop in microslip

从图6可以看出,在此种情形下,由于激励幅值较小,使得非线性力的最大值没有达到宏观滑移力,Iwan非线性模型发生微滑移现象.表1列出了激励幅值为1.5N时时频域交替法和中心差分法所得结果的比较.

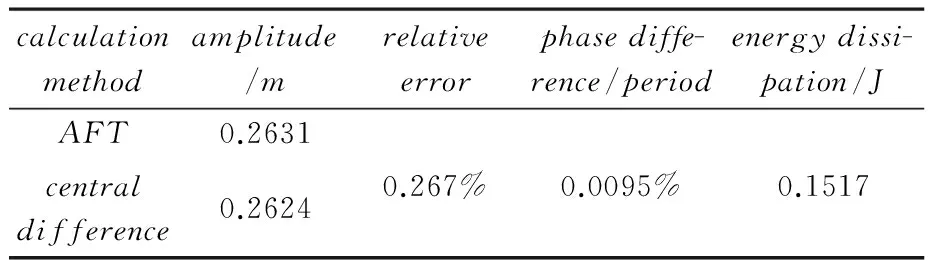
表1　模型微滑时不同方法所得结果的比较

第二种情况：f(t)=5sin(3t),结果下图所示.

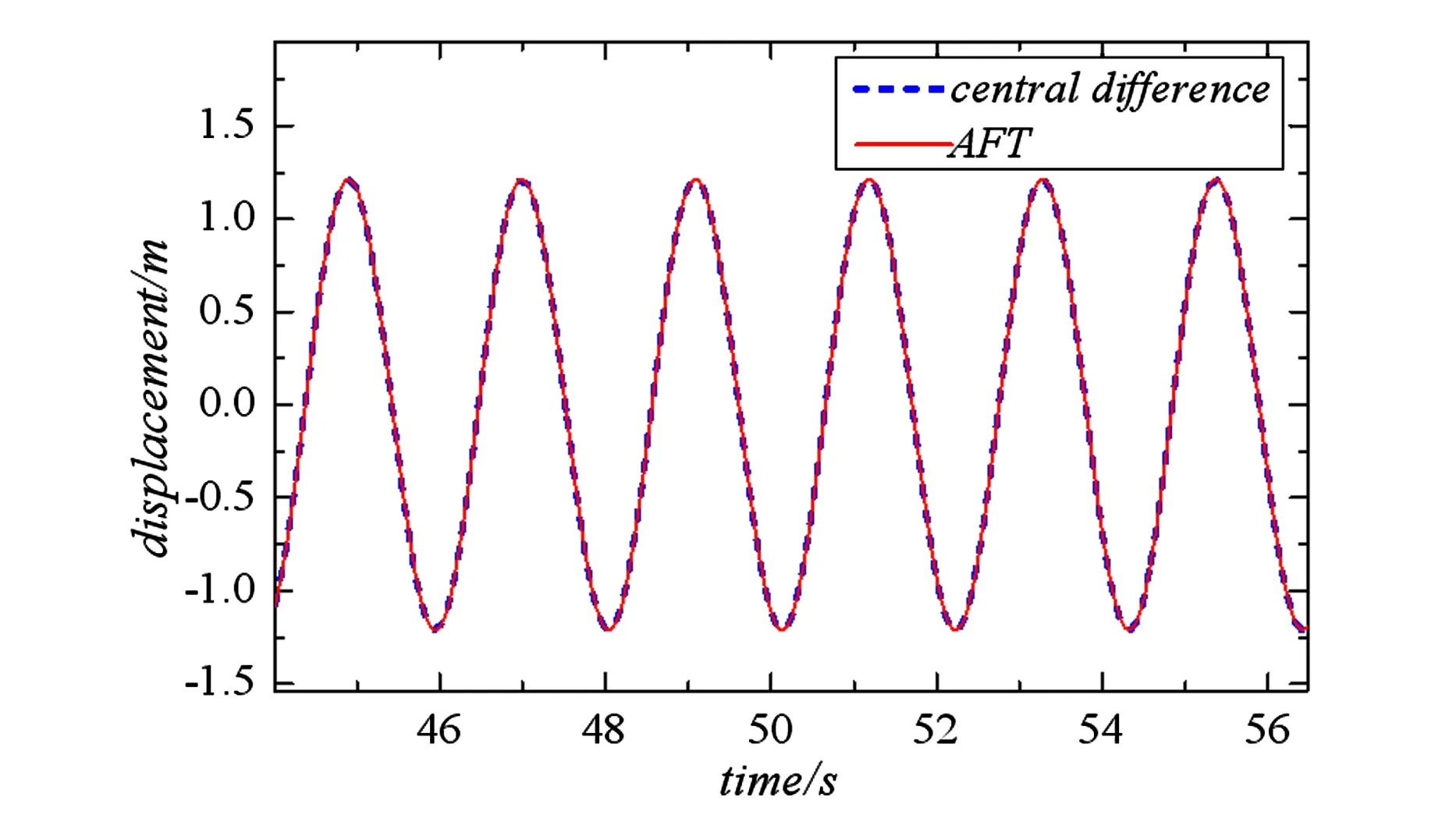
图7　模型宏滑时的稳态响应Fig.7　Steady-state response in macroslip

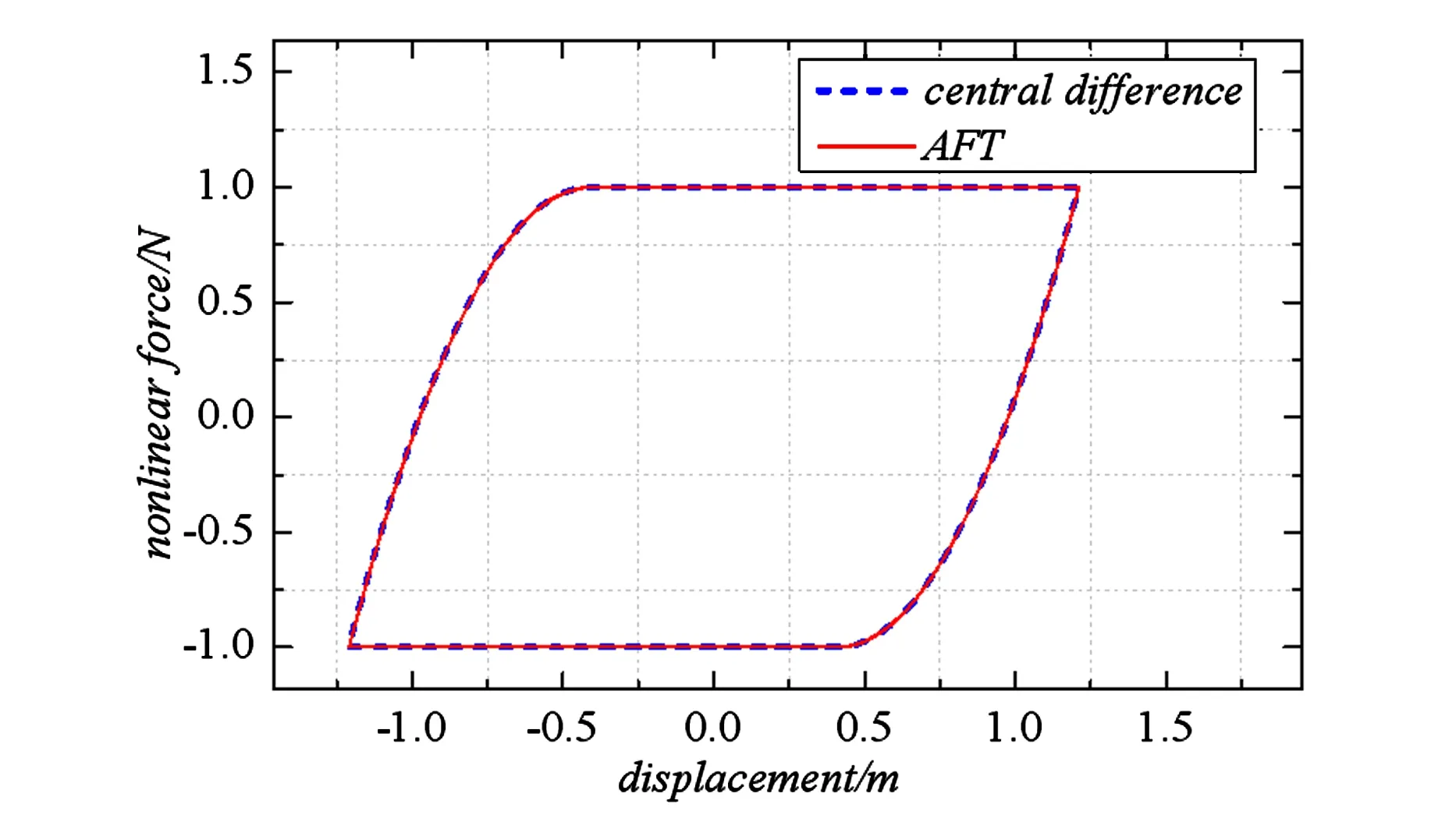
图8　模型宏滑时的迟滞曲线Fig. 8　Hysteresis loop in macroslip

当激励幅值增大后,系统稳态响应相应增大,从而使Iwan模型中更多的Jenkins单元发生滑移;从图8可以看出,此种情形下,非线性力的最大值达到宏观滑移力,Iwan模型发生宏观滑移.表2相较于表1结果误差较为明显,但此时计算精度仍很高.误差原因可能是非线性力的增大使得其对结果的影响程度变大.

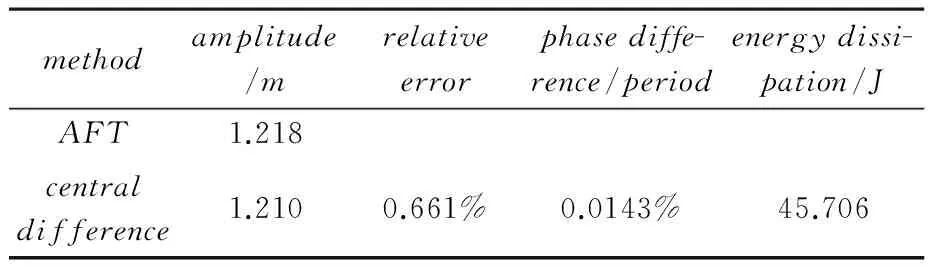
表2　模型宏滑时不同方法所得结果的比较

运用中心差分法对时频域交替法的计算结果进行验证,从上面两组计算结果可以看出,时频域交替法求得的单自由度振子系统稳态响应能与中心差分法的结果很好地吻合,说明了时频域交替算法适合求解此类非线性问题,而且计算的精度比较高.

下面通过求解系统的频响曲线和能量耗散,进一步研究Iwan非线性模型的特性.

从图9中可以看出,随着激励幅值的增大,频响曲线的峰值逐渐向左移动,而且频响曲线出现明显的软化现象,说明系统的固有频率降低了.导致这种现象的本因是Iwan模型的非线性特性,具体表现为激励幅值的增加使得Iwan模型中发生滑动的Jenkins单元数增加,从而导致振子系统的刚度降低,固有频率降低.在某些参数下,该模型的频响曲线也会发生非线性跳跃和多值现象.

图9　不同激励幅值下的频响曲线Fig.9　Frequency response diagrams with different excitation amplitudes

随着激励幅值的增大到一定程度,频响曲线中的部分频段内的响应就逐渐表现出线性系统的性质,即这一段内的不同激励下的频响曲线重合了.

从图10中可以看出,Iwan非线性模型的能量耗散随着系统稳态响应的逐渐增大而增大.微观黏滑状态下,非线性模型的能量耗散较小,且变化不大;宏观滑移状态下,非线性模型的能量耗散急剧增加.如果在双对数坐标系下绘制能量耗散,则曲线的斜率为3,这与一些连接结构的实验结果是一致的.

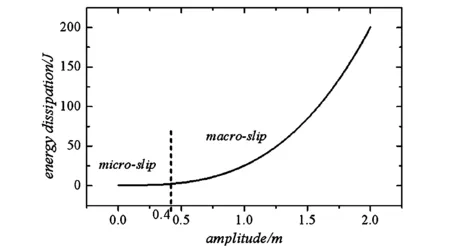
图10　模型能量耗散随响应幅值的变化曲线Fig.10　Energy dissipation-amplitude relationships

4　时频域交替法的收敛性、计算效率分析

在时频域交替法计算过程中,如何控制程序的收敛是保证算法计算效率的关键.本文选择的收敛性判别要求有两个,一是计算精度,包括两种算法稳态响应的相位差和稳态响应的幅值比较;另一个是计算效率,指计算所需时间的比较.

选用的收敛准则为：取前后两次迭代所得的稳态响应的一半长度(为了保证响应为稳态响应)进行相对偏差的分析,记前一次迭代得到的位移响应为数组A,后一次迭代得到的位移响应为数组B.利用相对偏差的大小来判断收敛性.相对偏差的定义为

(8)

选用激励f(t)=20sin(0.25t)来进行计算,取时间长度6000s,对不同的相对偏差值所对应的结果进行比较.

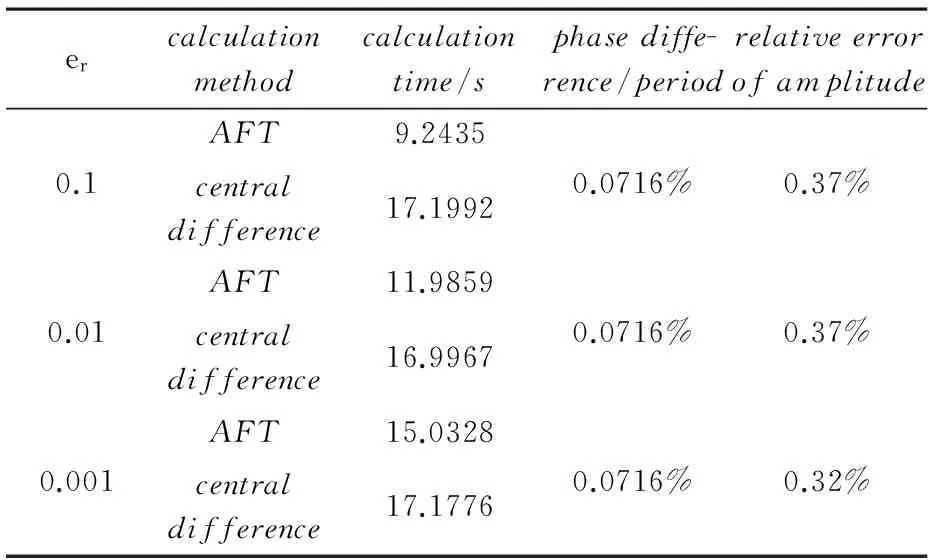
表3　不同er的相对误差比较

根据表3中数据的对比可以看出,相对偏差越小,时频域交替法的计算精度越高、但是计算耗费越大;本文选择相对偏差er=0.1作为算法迭代收敛的准则,这样既可以满足很高的计算精度,也能相对中心差分法而言提高计算效率.当然,如果需要保证更高的精度,可以选择更小的收敛准则,但是计算耗费则会很大.

此外,响应幅值和相位存在的微小误差可以通过调节采样频率进行降低.

5　结论

1)本文推导了时频域交替法求解含Iwan非线性模型单自由度系统稳态响应的具体公式和步骤.通过文中算例的验证及时频域交替法收敛性和计算精度的分析,显示出时频域交替法计算的结果与中心差分法的结果具有很好的一致性,说明了时频域交替法在求解非线性振动问题上具有明显的优势,不仅能满足较高的计算精度要求,而且求解效率较高,计算耗时减少约50%.

2)采用时频域交替法求解计算,得到了单自由度振子系统受迫振动的幅频响应曲线,图中表现出明显的软化特征,随着激励幅值的增加,系统的能量耗散增加,发生滑动的Jenkins单元数随之增加,系统刚度降低,固有频率降低.

1GaulL,LenzJ.Nonlineardynamicsofstructureassembledbyboltedjoints. Acta Mechanics Sinica,1997,125:169～181

2BergerEJ.Frictionmodelingfordynamicsystemsimulation. Journal of Applied Mechanics Reviews, 2002,55(6):535～577

3IwanWD.Adistributed-elementmodelforhysteresisanditssteay-statedynamicresponse. Journal of Applied Mechanics,1966,33(4):893～900

4ValanisKC.Atheoryofvisco-plasticitywithoutayieldsurface. Archive Mechanics, 1971,23(4):517～551

5WenYK.Methodofrandomvibrationofhysteresissystem. Archiwum Mechanics Division,1976,102(2):219～263

6SanliturkKY,ImregunM,EwinsDJ.Harmonicbalancevibrationanalysisofturbinebladeswithfrictiondampers. Journal of Vibration and Acoustics,1997,119(1):96～103

7HeK,ZhuWD.FiniteelementmodelingofstructureswithL-shapedbeamsandboltedjoints. Journal of Vibration and Acoustics-Transactions of the ASME, 2011,133(1):1～138GroperM.Microslipandmacroslipinboltedjoints. Experimental Mechanics,1985,25(2):171～174

9SegalmanDJ.ModelingjointfrictioninstructuralDyna-mics. Structural Control & Health Monitoring,2006,13(1):430～453

10CameronTM,GriffinJH.Analternatingfrequency/timedomainmethodforcalculatingthesteady-stateresponseofnonlinearsystems. Journal of Applied Mechanics,1989,56(3):149～154

11朱孟华. 求解非线性系统振动响应的Fourier正逆变换方法. 内燃机工程,1995,16(3):1～8 (ZhuMH.Amethodforsolvingthenon-linearvibrationsystemsbyfourierdirectinversetransformtechnique. Chinese Internal Combustion Engine Engineering, 1995,16(3):1～8 (inChinese))

*TheprojectsupportedbytheNationalNaturalScienceFoundationofChina(11372246).

†CorrespondingauthorE-mail:chao_xu@nwpu.edu.cn

02June2014,revised29June2014.

ALTERNATINGTIME/FREQUENCYDOMAINMETHODFORCALCULATINGTHESTEADY-STATERESPONSEOFHYSTERESISNONLINEARVIBRATIONSYSTEMS†

LiDongwuXuChao†

(School of Astronautics, Northwestern Polytechnical University, ShanXi, Xian710072, China)

Stick-slipandfrictionofthejointinterfacepayasignificantrolenotonlyonstructurenonlinearstiffnessanddampingbutalsoonstructurepassivedamping.Iwanmodelprovidesapreferablerecurrenceofthestick-slipandfrictioncharacteristicsofthejointinterface.Thealternatingfrequency/timedomainmethod(AFT)isusedtostudythesteady-stateresponseofsingledegreeoffreedomoscillatorsystemcontainingIwannonlinearmodelinthispaper.Thismethodtakesbothadvantagesoftheeffectivenessofcalculatingresponseforlinearsystembyfrequencydomainmethodandtheeaseofevaluatingnonlinearforcebytimedomainmethod.ThediscreteFouriertransformalternatingfromthetimedomaintothefrequencydomainisappliedthroughiteratingtoobtainthesteady-stateresponseofthesystem.TheresultofAFTiscomparedwiththatfromthecentraldifferencemethod,andtheinfluenceofexcitationamplitudeonnonlinearcharacteristicisalsoexaminedinthispaper.Theresultsshowthatthesteady-stateresponsebyAFTmethodagreeswellwiththatofthecentraldifferencemethod.Moreover,theAFTmethodperformsbettercomputationalefficiency,asthetime-consumingisreducedby50percent.Inawhole,itisfoundthattheapplicationofhigherexcitationamplituderesultsintheincreaseofthesystemenergydissipationandthereducesstiffnessandnaturalfrequency.

joint,hysteresisnonlinear,Iwanmodel,alternatingfrequency/timedomainmethod,steady-stateresponse

E-mail:chao_xu@nwpu.edu.cn

10.6052/1672-6553-2015-043

2015-06-02收到第1稿,2015-06-29收到修改稿.

*国家自然科学基金资助项目(11372246)