超导磁悬浮实验原理简析
2016-10-15路峻岭秦联华任乃敬
路峻岭, 秦联华, 顾 晨, 任乃敬
(清华大学 物理系,北京 100084)
超导磁悬浮实验原理简析
路峻岭, 秦联华, 顾晨, 任乃敬
(清华大学 物理系,北京100084)
超导磁悬浮现象的物理本质是超导体磁矩在轨道磁性峡谷或磁性陷阱的非均匀磁场中受到的电磁力与其重力的稳定平衡. 非理想第二类超导体块的磁矩由于钉扎作用在一定条件下既可表现为抗磁性磁矩又可表现为顺磁性磁矩,因此,它既可以实现磁悬浮又可以实现磁倒挂.
超导磁悬浮;磁倒挂;磁矩;钉扎作用;非均匀磁场
1 超导磁悬浮演示实验的操作、现象及相关疑问
‘超导磁悬浮列车演示实验’仪的结构如仪器照片所示.在环形钢板上并排黏贴3列永磁体磁钢片,由内向外按SNS极性排列,以形成磁性峡谷状环道,如图1所示.环形轨道侧面安装有转轴,可以方便地使环形轨道整体翻转,从而轨道的磁钢面也随之翻转(由在钢板的上面翻转到下面或相反).本实验所用的超导体是钇钡铜氧氧化物高温超导体块,属于非理想第二类超导体,转变温度为93 K(-180℃).它浸在液氮(-196℃)中即可转变为超导态.
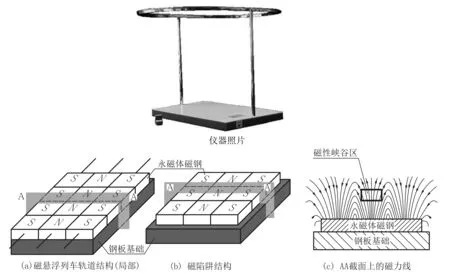
图1 磁性峡谷和磁陷阱结构示意图
在做磁悬浮实验时,先使轨道的磁钢面朝上,实验者用隔热夹把浸在液氮中的超导体块夹起并放在轨道上,它就在轨道的磁性峡谷中悬浮,轻轻地推它一下,它就悬浮在轨道的上方并沿轨道运动.如果戴上隔热手套用手向下压一压超导体块使它更靠近磁钢片,若它所处位置的磁场较弱(位置较高较远离磁钢片),它就在磁场力的作用下有少许回弹,在比原高度稍低的新的高度上悬浮;若它所处位置的磁场较强(位置较低较靠近磁钢片),它在磁场力的作用下有较大回弹,在与原高度几乎相同的高度上悬浮,而不能像压在弹簧上的物体那样总能够恢复到原来的高度.在超导体块悬浮运动的过程中,它的温度会渐渐升高,在到达转变温度时,它就变成正常态,不再悬浮,而落到导轨上或从导轨上掉了下来.
在做磁倒挂实验时,先要将轨道翻转,令磁钢面朝下,再用隔热夹把浸在液氮中已转变为超导态的超导体块夹起,放到实验者戴着隔热手套的手上,实验者手推超导体块使它从下方贴近轨道的磁钢面(磁场较强区),松手,它就在比轨道磁钢面略低的位置上倒挂悬浮于轨道的磁性峡谷中了,轻轻地推它一下,它就悬浮着倒挂在轨道的下方并沿轨道运动.它倒挂悬浮的位置比轨道的磁钢面稍低(磁场稍弱区).在超导体块倒挂悬浮运动的过程中,它的温度会渐渐升高,在到达转变温度时,它就转变成正常态,不再悬浮,而从悬浮点处掉了下来.
如何理解上述实验现象呢?如果说,已经转变为超导态的超导体块由于完全抗磁性能够悬浮在轨道磁钢的磁场中,那么磁倒挂时磁场对超导体块的吸引力又是来自何方?以下从原理分析入手,对以上实验现象给出一种解释.
2 关于超导磁悬浮列车演示实验原理
2.1超导物理研究简介[1-3]
物质的超导电性是在大约一个世纪以前,由荷兰莱顿大学的科学家们在研究低温现象的过程中偶然发现的.1908年7月10日下午6:30,在莱顿实验室第一次实现了氦气的液化,温度到达4 K左右.1911年昂尼斯(H.K.Onnes)等人在测量低温下纯汞的电阻时发现,在约4.2 K时电阻突变为零,这完全出乎人们的意料.材料电阻突变为零的现象被称为超导电性.在随后的几年里,他们研究了各种金属材料的超导电性,确定:这是物质的一相,如同气相液相固相一样,并把这种状态称为超导相或超导态.影响超导相的因素主要是温度Tc和磁场Hc,另外还有通过该材料的电流密度Jc,即物质处于图2曲面三棱锥区间内的状态就是超导态[1],其中Tc、Hc和Jc分别是临界温度、临界磁场强度和临界电流密度.实际上,由于电流能够产生磁场,电流密度Jc对超导态条件的限制是由于它产生的磁场的影响.
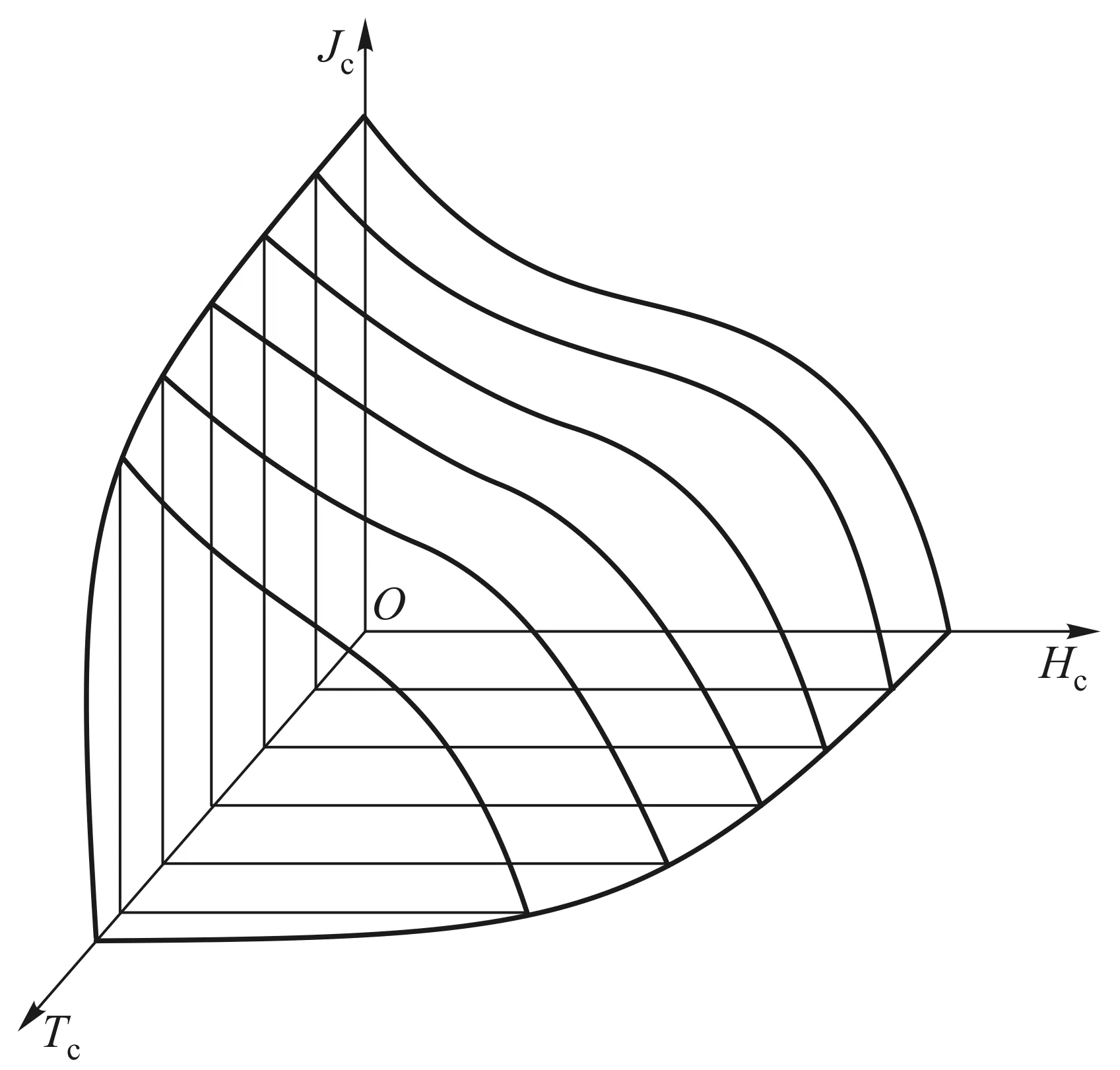
图2 超导域示意图
1933年德国科学家迈斯纳(W.Meissner)和奥森菲尔德(R.Ochsenfeld)通过实验证实了超导态具有完全抗磁性,即超导体内的磁场总是零.超导态的零电阻性和完全抗磁性是它的两个基本的独立物理属性.超导态的完全抗磁性又称为迈斯纳效应,其具有完全抗磁性的状态又称为迈斯纳态.
1935年,伦敦兄弟(F.London & H.London)在迈斯纳效应的启示下,从理论上研究超导态的电磁学特性,提出了著名的伦敦方程.伦敦方程可以很好地解释超导态的超导电性和完全抗磁性,同时预言外磁场在超导体中的穿透深度的存在,即完全抗磁性只存在于离开界面一定深度以内,外磁场可以深入到超导态表面的一定深度.1939年,此预言被实验所证实[3].
1950年,金兹堡(V.L.Ginzburg)和朗道(L.D.Landau)在二级相变理论的基础上提出了一个唯象的超导理论(G-L理论),其独到之处是对超导态的描述引进了一个有效波函数作为复数序参量,波函数的模的平方等于超导电子密度.由G-L理论,还引入了G-L参量κ=λ(T)/ξ(T),可据此决定超导态与正常态之间界面能的正负,进而确定两类超导体的划分.其中,λ(T)为外磁场在超导体中的穿透深度,ξ(T)为超导态电子波函数的相干长度.
1957年,美国科学家巴丁(J.Bardeen)、库柏(L.N.Cooper)和施里弗(J.R.Schrieffer)根据两个电子通过晶格声子可以存在净吸引作用而形成库柏对,而库柏对在周期性晶格场中运动无散射(表示零电阻)的图像,建立了超导的量子微观理论[2,3],最终揭示了超导现象的秘密.BCS理论现在已为世界科学界所公认.因此,超导现象是一种宏观量子现象.此后关于超导的研究,基本上是以寻找能够在强磁场上实用的高温超导体材料为目的而在进行着的,当然也包括关于超导量子干涉器件的研究.
2.2非理想第二类超导体
早期对超导的应用研究总想利用超导材料的零电阻性得到强磁场.但往往事与愿违,材料中的电流在尚未使超导线圈产生所要求的强磁场时,线圈材料已经由迈斯纳态变成了正常态.1937年,舒布尼科夫(L.V.Shubnikov)在对超导合金的实验研究中,首次观察到在临界温度以下在外磁场从弱变强的过程中,超导体由迈斯纳态转变为正常态的过程中间要经过一个新的超导状态—混合态[2,3].处于混合态的超导体中可以有磁场通过,但仍保持零电阻性.如果以Hc1表示材料由迈斯纳态变为混合态时的临界磁场,以Hc2表示材料由混合态变为正常态时的临界磁场,则Hc2比Hc1大得多,这为工程应用提供了一幅美好的前景.在差不多同一个时期,莱顿实验室的哈斯,牛津的基利的人也在实验中发现了类似的现象[3].1950年,苏联科学家阿布里柯索夫(A.A.Abrikosov)在G-L理论的基础上,从理论上说明了这类超导体的特点和性质,并把这种超导体称为第二类超导体,而把没有混合态的超导体称为第一类超导体.两类超导体的相图如图3所示.以下分3步说明第二类超导体的物理特性[3,4].
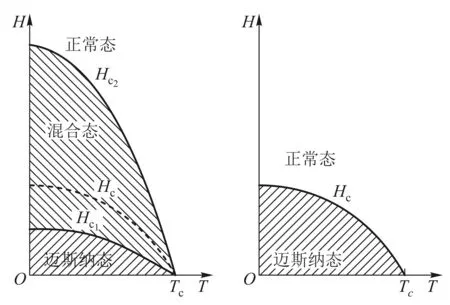
图3 两类超导体的相图
2.2.1超导态的吉布斯自由能
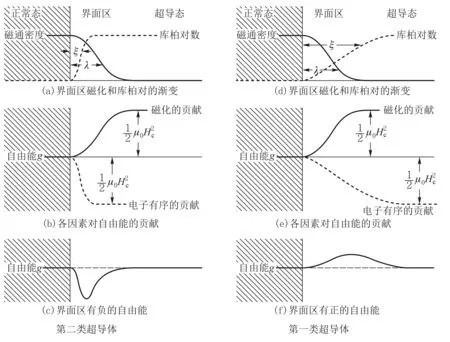
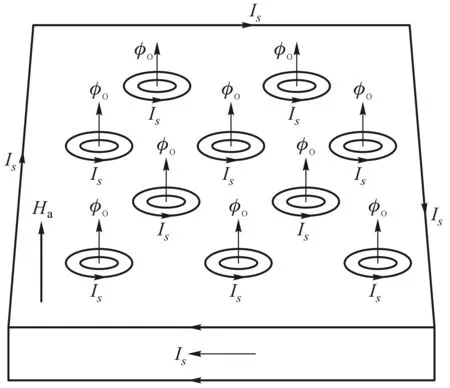
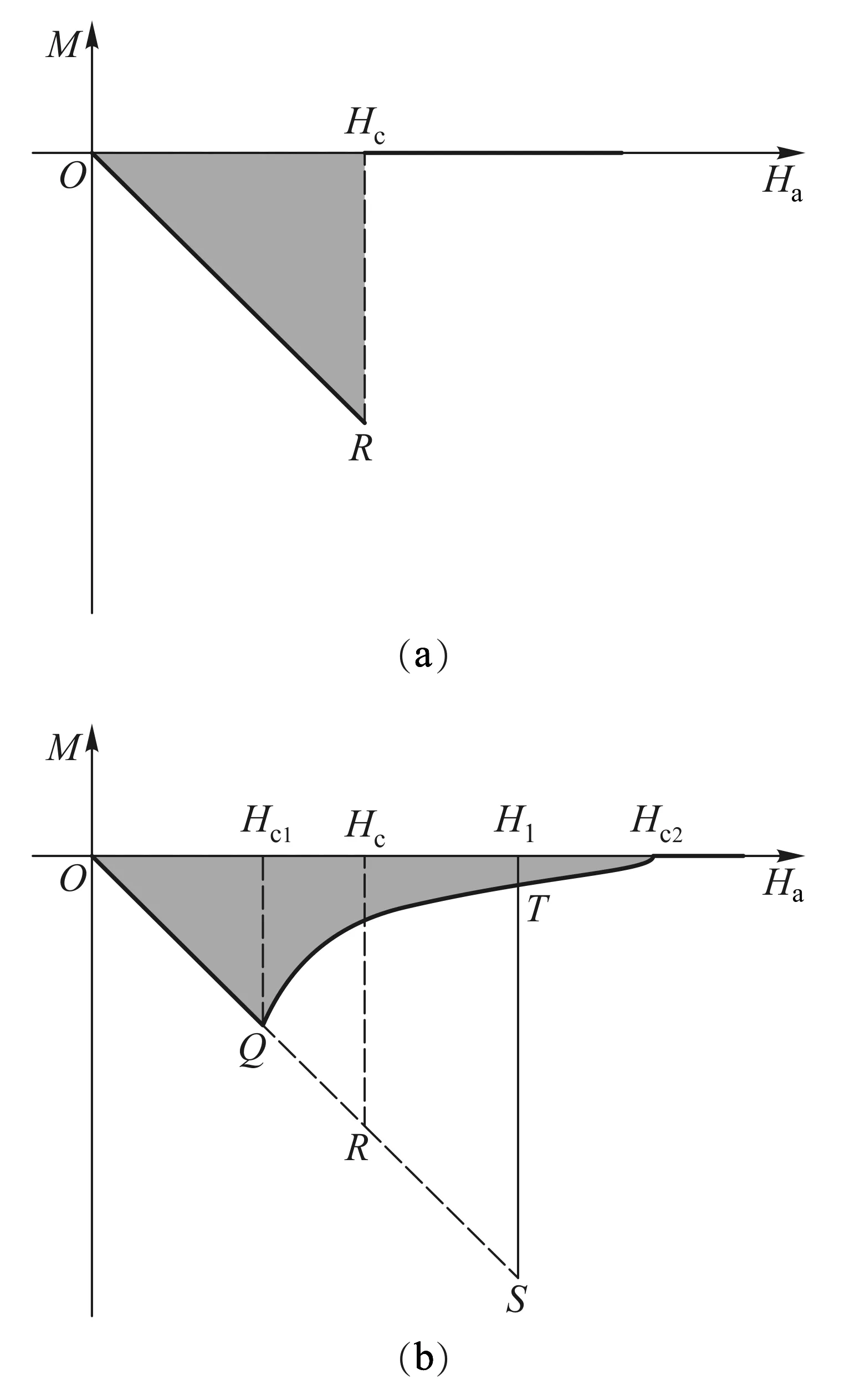
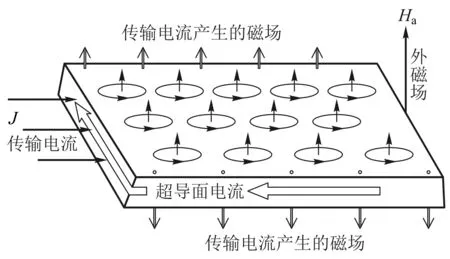
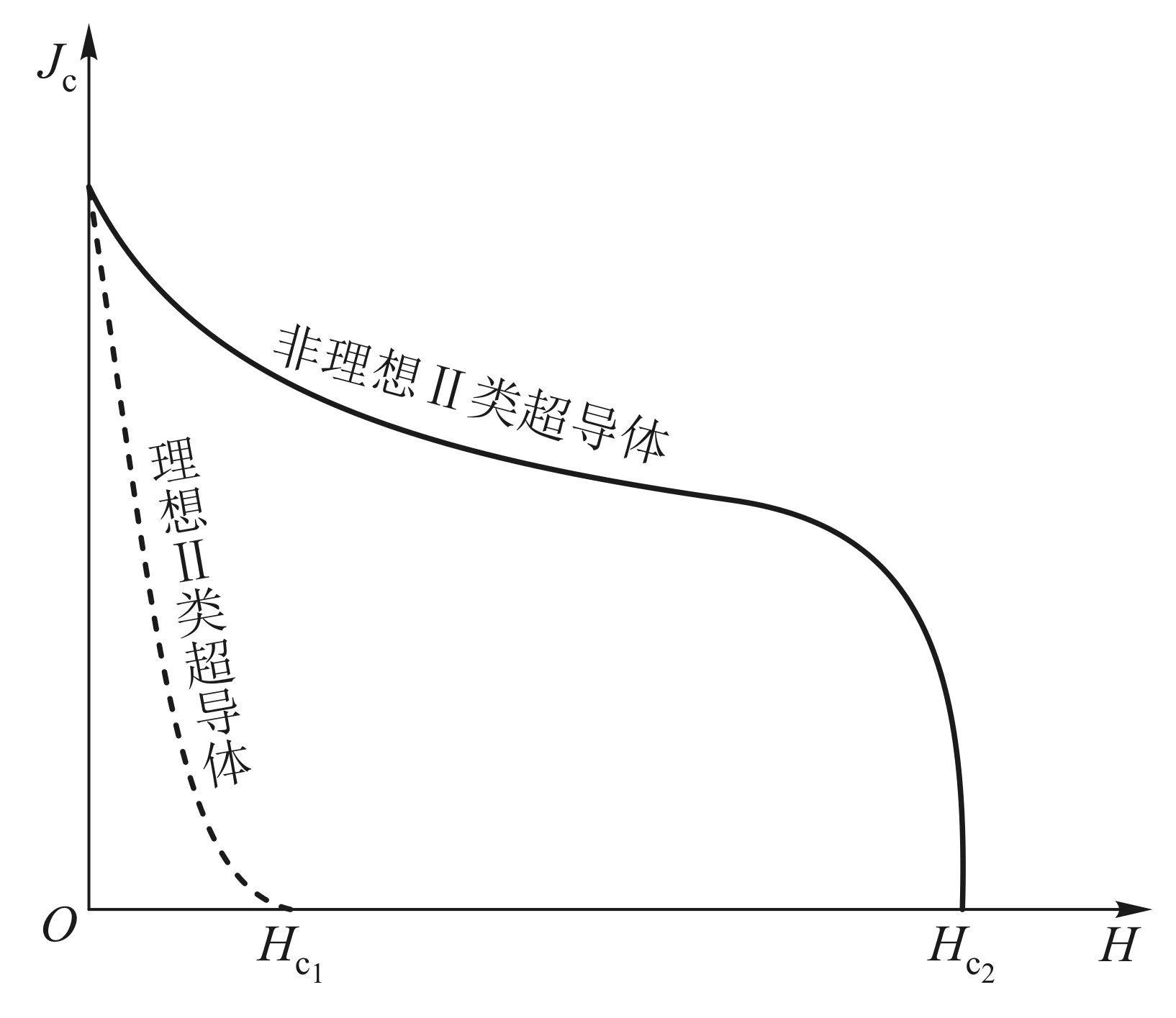
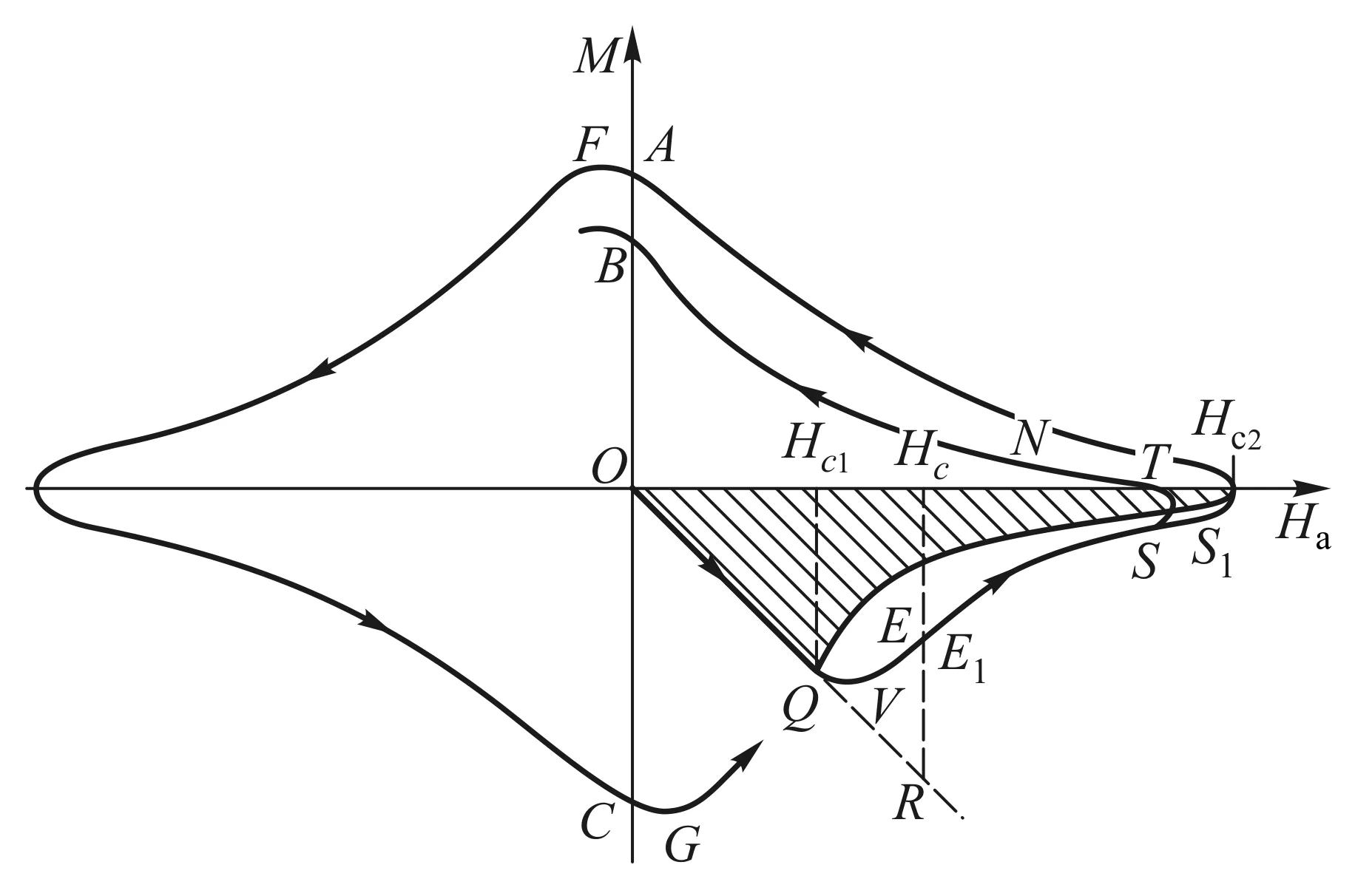
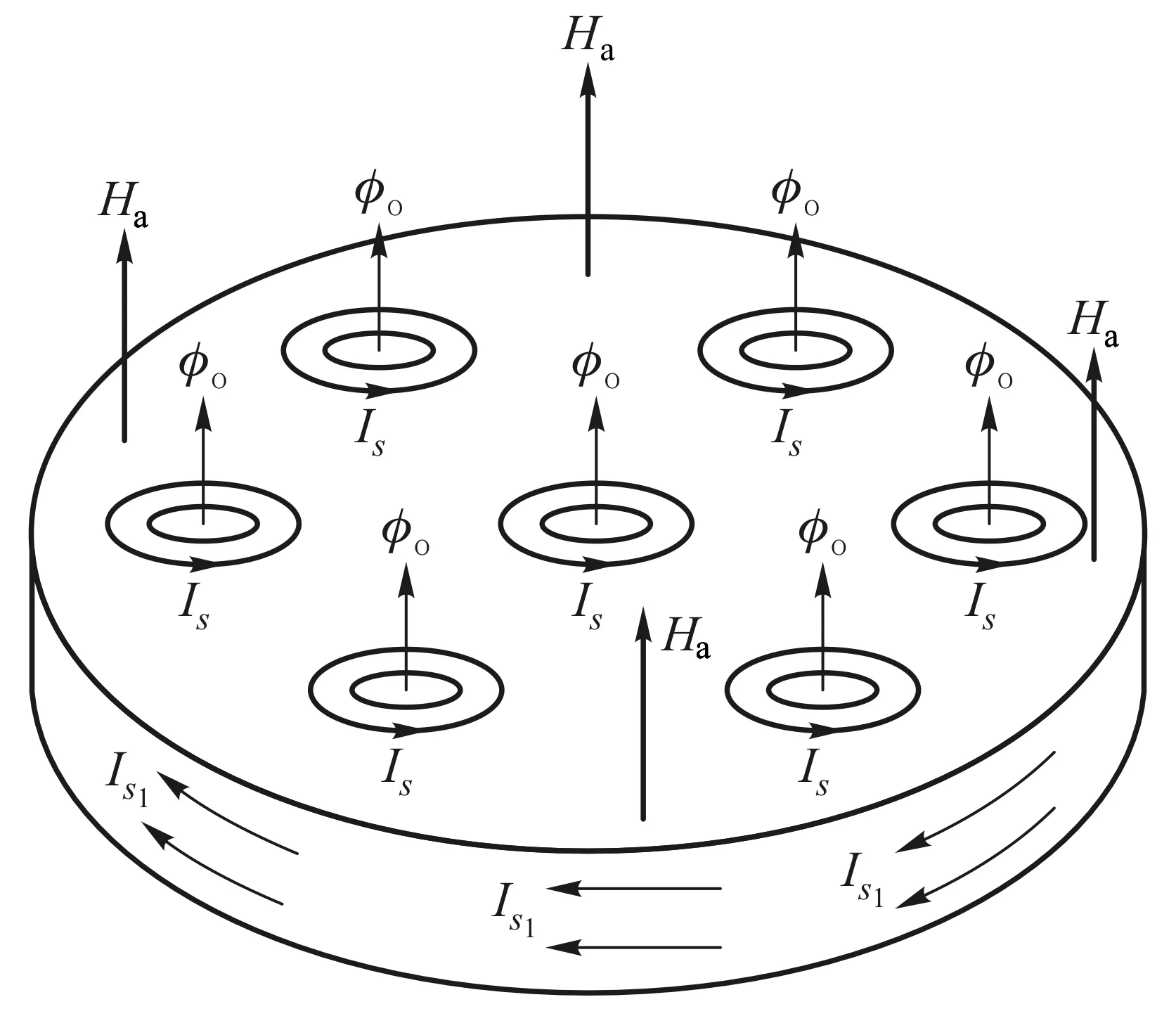
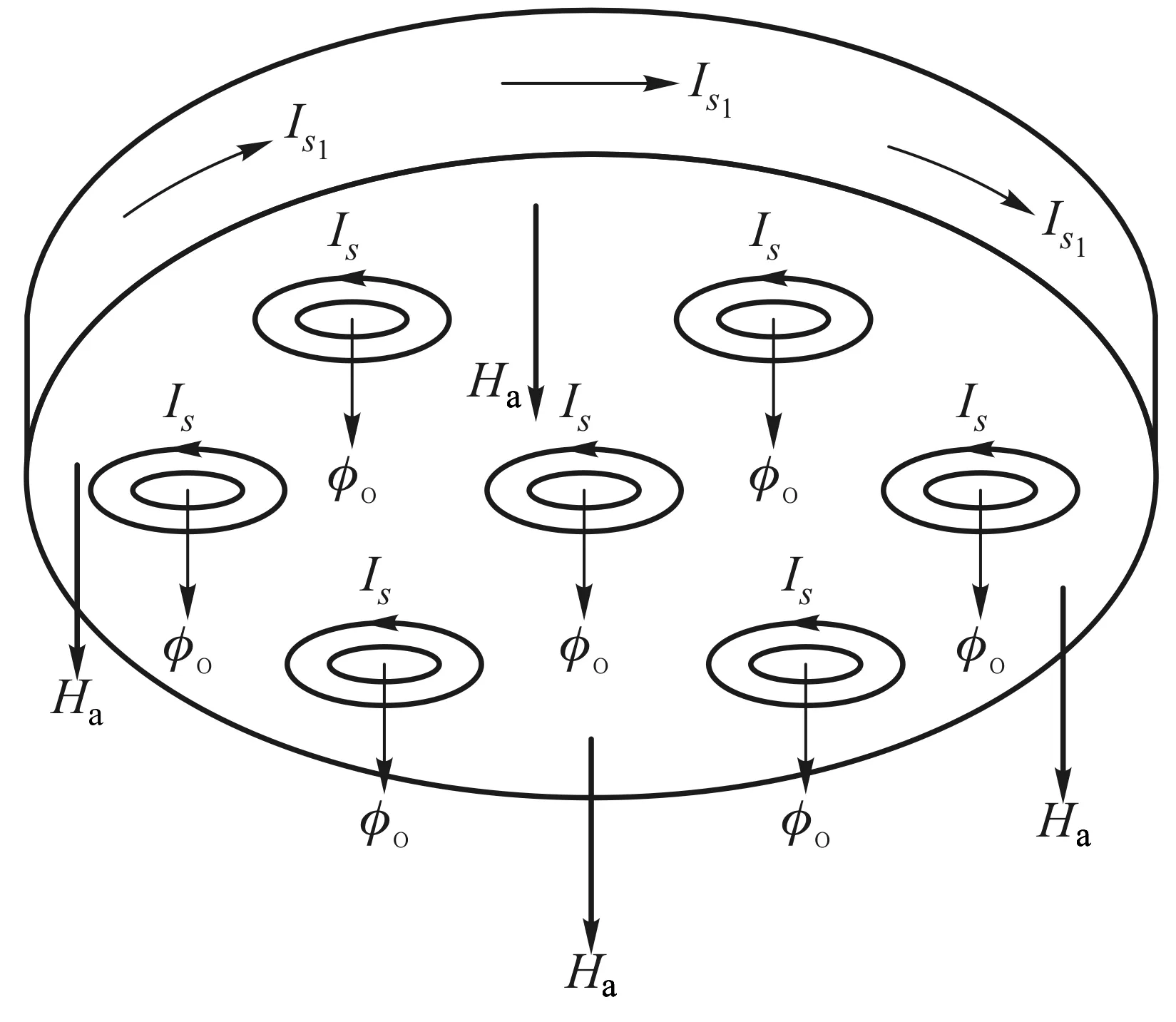
设物态变化的过程为等温等压过程,判断此过程自发变化方向的态函数为吉布斯自由能.考虑一根长直超导体圆柱形样品,设外磁场H=0,当温度T gs(T,H)-gs(T,0)= (1) 其中,用到了超导态的完全抗磁性,即磁化强度M=-H.当H→Hc时,超导体即由超导态自发变为正常态.也就是说,当H=Hc时,超导态的吉布斯自由能密度应等于正常态的吉布斯自由能密度,即 gs(T,Hc)=gn(T,Hc) (2) 由于超导体为正常态时是通常的弱磁质,磁化过程引起的磁能密度的变化可以忽略不计,因此可以认为超导体处于正常态时的自由能密度几乎与外磁场强度无关.故有 gn(T,0)=gn(T,H)=gn(T,Hc) (3) 根据这一理解,可画出超导体的吉布斯自由能密度与磁场强度的关系曲线如图4所示[3].由图中可知 (4) 图4 超导体的吉布斯自由能密度g与磁场强度H的关系曲线 2.2.2具有负界面能的第二类超导体及其混合态的物理图像 由于外磁场在超导体中的穿透深度的存在,说明在超导体的界面区,库柏对(超导电子)密度和磁场都是渐变的.假设在超导体中存在着一个界面,界面一侧为正常态,另一侧为超导态,则在两种物态之间必定存在着一个界面区,在界面区中磁通密度和超导电子密度(库柏对数密度)必定是渐变的.设它们的渐变尺度分别以ξ、λ表示,含义是库柏对密度在ξ的空间尺度(对应超导态电子波函数的相干长度)上有显著的变化;磁通密度在λ的空间尺度上有显著的变化,如图5(a)与图5(d)所示.在热平衡时超导体在界面上两种物态的吉布斯自由能应该相等.图5(b)与图5(e)示出影响自由能的两因素在界面区的变化, 图5 正常态与超导态的界面能示意图 (4) (5) 这就是第二类超导体的下临界磁场Hc1.若外磁场继续增大,至另一临界值Hc2,正常芯遍布于超导体,超导体的状态即由混合态变为正常态,Hc2称为第二类超导体的上临界磁场.可以证明[2,3], (6) 上述理论解释了第二类超导体的如图3所示的相变特性. 对第二类超导体片沿厚度方向加一磁场Ha,若Hc1 (7) 图6 第二类超导体出现混合态时的物理图像 相邻正常芯的涡状超导电流之间总是相互排斥的.除了围绕正常芯的涡状超导电流外,超导体表面仍如第一类超导体一样存在面超导电流以保持正常芯之外的区域的完全抗磁性(磁场为零).相互排斥的涡状超导电流使得正常芯在超导体表面呈现规则的平面三角形点阵结构.这种由正常芯构成的点阵结构已由艾斯曼(V.Essmann)和特劳布尔(Trauble)等人用实验的方法证实,他们将很微小的铁磁粉,放在处于混合态的第二类超导体的表面,从而显示出正常芯分布的点阵图案来.理想第二类超导体作为磁介质,其磁化曲线如图7(b)所示.为了作对比,同时画出了第一类超导体的磁化曲线如图7(a)所示.由于完全抗磁性,第一类超导体的磁化曲线为第四象限的角分线,由原点到R点,外磁场到达临界磁场Hc,超导态即变为正常态.第二类超导体的磁化曲线则复杂得多.当外磁场由零逐渐增大时,第二类超导体的磁化开始是沿第四象限的角分线,由原点到Q点,此过程的磁化与第一类超导体相同,超导态为完全的迈斯纳态.当外磁场到达下临界磁场Hc1时,磁通可以穿过超导体,超导体的状态为混合态,相当于完全抗磁性附加上了顺磁磁矩,磁化强度的绝对值开始减少.例如,当外磁场强度到达H1时,若按照完 全抗磁性其磁化曲线应该到达S点,而实际上它却到达了T点,线段ST就表示由于正常芯的出现而产生的顺磁性磁化强度,线段TH1就表示第二类超导体实际的总磁化强度,它仍然为负值,说明此时的第二类超导体仍然是抗磁质.当外磁场强度继续增大,到达上临界磁场Hc2时,超导态即变为正常态.在上下临界磁场之间存在一个外磁场强度Hc,它是假定第二类超导体为第一类超导体时的临界磁场,即图7(b)中三角形ORHc的面积等于第二类超导体磁化曲线与Ha轴所围曲边三角形的面积,为了理论分析方便,定义Hc为第二类超导体的热力学临界磁场.上述第二类超导体的Hc都是指此热力学临界磁场. 需要指出的是,上述这两种超导体的磁化规律都是可逆的,即随外磁场Ha由零逐渐变大,磁化强度M随之变化,在到达某一种状态(Ha,M)时,若外磁场随即逐渐减小,磁化强度M也随之减小,各种状态将完全无误地重复原过程又回到原点.在磁化曲线上将表现为沿原路返回. 图7 理想第二类超导体的磁化与第一类超导体的比较 2.2.3非理想第二类超导体中结构的不均匀性对磁通线的钉扎作用及其影响 第二类超导体的上临界磁场Hc2虽然比第一类超导体的临界磁场Hc高了许多,但是它还是不能应用于强磁场超导材料,这主要是由于一旦存在传输电流其零电阻性不能够保持且其临界电流值Jc太小.以下简单介绍其中的物理原因. 如图8所示,设处于低温下的第二类超导体片在外磁场Ha的作用下已是混合态,此时通以传输电流,电流密度为J.由于传输电流也要产生磁场,且在超导体片上的左右两侧(左右以J为参考)该磁场的方向相反,与外磁场Ha叠加所得合磁场将是左强右弱,因而必然使得混合态中的正常芯的密度不同,也将是左密右疏,正常芯的超导涡电流的相互排斥作用必然使得较密区域的正常芯向较稀疏的区域运动.正常芯的移动就是磁通线的移动.磁通线在导电的混合态中的移动必然由于电磁感应而在其中产生感生电动势,感生电场的方向与传输电流的方向一致.注意到感生电场有作用的区域中有大量正常芯存在,即沿电流传输方向的电势将下降,要出现电阻效应.这种由于磁通线的移动而产生的电阻效应称为流阻.据估算,第二类超导体片混合态流阻的电阻率竟超过了电解铜的电阻率.混合态中磁通线的移动使得其临界电流值Jc大大减小.所以,此类超导体仍不能用于强磁超导材料. 图8 理想第二类超导体中传导电流对正常芯的影响 自上个世纪60年代以来,人们在不断地寻找强磁超导材料,后来发现了一类超导材料,它属于第二类超导体,但它没有流阻效应,也就是说,在一定临界电流以下,其混合态中没有流阻,其物理本质是在有传输电流的情况下没有磁通线的移动.大量实验研究和理论分析发现,造成磁通线不能移动的原因在于这种材料结构的不均匀性.由于加工、热处理、掺杂等因素的不尽完美,材料结构上出现了许多缺陷、杂质、析出物等异常畴(局部异常区域),众多的异常畴的存在阻止了磁通线的移动.于是,这一类超导材料被称为非理想第二类超导体.为什么材料结构上的不均匀性能够阻止磁通线的移动呢?从物理上说,就是正常芯磁通线通过异常畴时总的吉布斯自由能比不通过时更低,正常芯从通过异常畴的状态走出来需要一定的能量和一定的力,这种力就是与外磁场Ha和传输电流J相关的洛伦兹力.非理想第二类超导体材料结构的不均匀性十分敏感地与加工工艺相关.典型的非理想第二类超导体临界电流Jc与外磁场Ha的关系曲线如图9所示,可见,非理想第二类超导体的混合态临界电流Jc比理想第二类超导体的Jc大得多[3,4]. 图9 非理想第二类超导体临界电流与外磁场的关系 非理想第二类超导体材料结构的不均匀性反映在有大量异常畴的存在,正常芯磁通线在这样的材料中运动如同在一条坑坑洼洼高低不平的公路上运动一样,前进难,后退也难,磁通线向这类超导体进入难变动也难.当正常芯磁通线陷进异常畴时,如同被钉扎着一样,因此,非理想第二类超导体结构上的异常畴对正常芯磁通线运动的阻止被称为钉扎作用[2,3,5].钉扎作用使非理想第二类超导体的磁化特性与理想第二类超导体有显著差别.第一类超导体与理想第二类超导体的磁化都是可逆的,见图7,而非理想第二类超导体的磁化特性则表现为磁滞迴线, 如图10所示.为了进行对比,图10中也画出了理想第二类超导体的磁化曲线(阴影区)[3,4]. 图10 非理想第二类超导体的磁化曲线 当处于低温的非理想第二类超导体片在沿厚度方向的外磁场Ha由零逐渐增大到Hc1时,磁化曲线由原点沿第四象限的角分线变化到Q,这一过程反映完全抗磁性,其超导态为迈斯纳态.随Ha继续增大,超导态变为混合态.由于钉扎作用,磁通线不能一下子进入超导体,过程QV表现为磁化强度M绝对值的仍在继续变大,至V点到达最大.随Ha继续增大,磁通线进入超导体越来越多(正常芯越来越多),磁化曲线将变得使磁化强度M的绝对值逐渐变小.由于钉扎作用,此时正常芯不如理想第二类超导体在同样过程同样Ha时生成得多,因此非理想第二类超导体的磁化曲线较理想第二类超导体的磁化曲线离开横轴(Ha轴)要远一些(在下方).当Ha继续增大到Hc2时,正常芯充满整个超导体,超导态变为正常态,磁化强度M变为零.若此时减小外磁场Ha,维持抗磁性的超导体的超导面电流将渐渐变小,而由于钉扎作用,表现出顺磁性的正常芯数目却变化不大,这时整个超导体将表现出顺磁性来,这就是磁化曲线在第一象限的变化规律.当外磁场Ha减小到零时,钉扎作用会使超导体内有一部分正常芯仍然保持,即存在剩磁,这就是磁化曲线到达A点时的情况.若此时加上反向外磁场Ha且使之由零开始渐渐增大,由于钉扎作用,正常芯的数密度变化不大;但体现抗磁性的超导面电流将会出现,因它随磁场改变方向也改变了方向,它加强了超导体的顺磁性,磁化曲线到达F点,整体的顺磁磁化强度达到极值.若反方向的外磁场Ha继续增大,反向的正常芯磁通线将逐渐增多,出现如同第四象限类似的情况,只是方向相反.外磁场Ha完成正反方向由小到大由大到小的变化,非理想第二类超导体的磁化曲线则完成一周迴线过程.若外磁场Ha从尚未到达上临界磁场Hc2但又较强的位置S点开始减小,由于钉扎作用,则体现顺磁性的正常芯数目变化不大,而体现抗磁性的超导面电流将减小而使磁化过程沿STB曲线运动,整个超导体将表现出顺磁性来,这便是磁倒挂悬浮能够出现的物理原因. 可见,处于混合态的非理想第二类超导体片,在沿厚度方向的外磁场Ha的作用下的磁化规律,主要体现在反映抗磁性的超导面电流的影响和反映顺磁性的正常芯的影响,前者只与外磁场Ha的大小有关且是可逆的,而后者由于钉扎作用而不可逆,它不但与外磁场Ha的大小有关而且还与磁化过程有关,超导体总体的磁化特征则是两者共同作用的结果. 2.3关于磁悬浮和磁倒挂悬浮实验 磁悬浮和磁倒挂悬浮现象的本质是超导体块受到的电磁力和重力的稳定平衡.在这里需要说明的是电磁力.本实验涉及的电磁力是磁矩(磁偶极矩)在非均匀磁场中的受力.在本实验中,由于磁性轨道是在环形钢板上并排黏贴三列永磁体磁钢片(由内向外按SNS极性排列)形成的磁性峡谷,超导体块在其中如同在峡谷中的物体,在沿轨道的横向运动时会受到峡谷壁的阻挡(楞次定律);在沿垂直于磁钢面的方向运动时,会受到电磁力和重力的共同作用,当电磁力和重力刚好平衡时,超导体块就实现了悬浮或倒挂,使它只能沿轨道运动.若置轨道面为水平面,在垂直于磁钢面的方向(竖直方向)作z轴,以磁钢面为原点,则越远离磁钢面(沿z增大方向变化)磁场强度Ha越小,且磁场强度沿z方向的变化率也越小.在本实验中,超导体块能够实现悬浮或倒挂的关键是超导体块的磁矩在磁钢的非均匀磁场中受到了电磁力.超导体块在轨道磁场中磁化而具有一定磁矩Pm(磁化强度M乘以体积V),磁矩Pm受到轨道非均匀磁场的作用力(与重力方向相反的力)而与重力相平衡,才能实现悬浮或倒挂. 根据电动力学的相关知识,磁矩Pm在非均匀磁场中的受力为[6] (8) 式中,设超导体块是均匀磁化的,磁矩Pm=VM,V为其体积,M为磁化强度矢量. 图11 超导体磁悬浮实验时的模型简图 在做磁悬浮实验时,轨道的磁钢面朝上,轨道磁场Ha沿竖直方向向上(z轴正方向),超导体位置z越大,磁场强度Ha越弱,即沿z方向磁场强度Ha的变化率为负值;且离磁钢面越远,磁场强度Ha的变化率的绝对值越小.当实验者把处于低温的超导体(已转变为超导态)放在轨道上,它就处于轨道的磁性峡谷中了.轨道磁场Ha将使超导体磁化,由于抗磁性其磁矩Pm将沿负z方向(竖直向下),据式(8)它受到的电磁力方向向上,而重力竖直向下.开始在离磁钢面较远处,电磁力小于重力,超导体将下降,随着高度降低,磁场变强,抗磁磁矩的绝对值变大,到某一z值,电磁力和重力平衡,超导体就悬浮在轨道上面了,超导体的磁性特征如图11所示.轻轻一碰,超导体就悬浮着沿轨道运动.若此时轻轻按压,其位置如图10中从E位置到达E1位置,E1位置的磁场较E位置更强,正常芯将出现得更多,它的磁矩的绝对值将变小,所以此时在原来位置它就不能保持悬浮了,只能在较低位置(磁场强度Ha的变化率的绝对值较大)才能实现悬浮.若在较低位置(磁场较强)轻轻按压悬浮着的超导体,其位置如图10中从S位置到达S1位置.虽然S1位置的磁场较S位置更强,但此时正常芯接近饱和,进一步再增加得不多,它的磁矩的绝对值基本不变,而S1位置的磁场强度Ha的变化率的绝对值大于S位置的,所以此时它在S1位置时受到的电磁力大于重力,它要上浮到S位置才能再次实现悬浮.这就是我们看到的实验现象. 图12 超导体磁倒挂实验时的模型简图 在做磁倒挂实验时,轨道磁钢面朝下,轨道磁场Ha沿竖直方向向下(z轴正方向),实验者戴上隔热手套,手推超导体使它从下方贴近轨道的磁钢面,松手,如图10中从磁场很强的S位置松手.由于重力和电磁力(斥力)同方向,都是竖直向下方向(z轴正方向),此时它不可能在此处倒挂悬浮,重力和电磁力的合力使它下降.由于体现抗磁性的超导面电流随磁场强度的减小而减小,而体现顺磁性的正常芯数目由于钉扎作用而基本不变化,超导体的磁矩由负变正.其位置如图10中从S穿越横轴到达N点.此时,超导体的磁矩Pm方向向下(z轴正方向),即Pm大于零,磁场强度Ha的变化率小于零,所以超导体磁矩受力向上(小于零),与重力方向相反.在磁场强度Ha的变化率的大小适当的位置,例如N点,重力与电磁力平衡,即可实现磁倒挂悬浮现象,即超导体需由磁场强处移到磁场弱处才能实现倒挂悬浮.此时超导体的磁性特征如图12所示.轻轻一碰,超导体就在磁钢下方悬浮着沿轨道运动.这就是我们看到的实验现象. 超导磁悬浮现象的物理本质是超导体磁矩在轨道磁性峡谷或磁性陷阱的非均匀磁场中受到的电磁力与其重力的稳定平衡. 非理想第二类超导体块的磁矩由于钉扎作用在一定条件下既可表现为抗磁性磁矩又可表现为顺磁性磁矩,因此,它既可以实现磁悬浮又可以实现磁倒挂.要实现稳定平衡,磁性峡谷轨道或磁性陷阱是必要的. 磁悬浮实验需要超导体具有抗磁性磁矩,原则说来,第一类超导体、理想第二类超导体和非理想第二类超导体都有可能实现磁悬浮,只要外磁场不超过临界磁场. 磁倒挂悬浮实验需要超导体具有顺磁性磁矩,只有非理想第二类超导体才可能实现磁倒挂悬浮实验. 在磁悬浮实验中,超导体块在离开轨道磁钢上方的任意距离上,所受的电磁力都是排斥力,即:超导体块所受的电磁力总是使它远离轨道磁钢,离轨道磁钢越近排斥力越强,越远排斥力越弱直至消失.而在磁悬浮倒挂实验中,超导体块在离开轨道磁钢下方的距离上,由近往远,它所受的电磁力起初是排斥力,依次为不受力,最后是吸引力,再随着远离轨道磁钢的距离的增大此吸引力将逐渐消失.因此,本实验所用超导材料为非理想第二类超导体材料是十分必要的. [1]I.M.弗思.超导电性 [M].伍凌武,译.北京:科学出版社,1977:1-5. [2]章立源,张金龙,崔广霁.超导物理学[M].北京:电子工业出版社,1995:1-6,94-96,101,186-190. [3]林德华.超导物理基础与应用[M].重庆:重庆大学出版社,1992:32-39,44-47,57-64,84-100. [4]米克秒.超导电性及其应用[M].北京:科学出版社,1980:46-72. [5][美]M.廷哈姆.超导电性导论[M].邵惠民,等译.北京:科学出版社,1985:32-39,208-214. [6]郭硕鸿.电动力学[M].2版.北京:高等教育出版社,1997:118. A brief analysis for the principle of superconducting magnetic levitation experiments LU Jun-ling, QIN Lian-hua, GU Chen, REN Nai-jing (Department of Physics, Tsinghua University, Beijing 100084, China) The phenomenon of superconducting magnetic levitation is essentially that the force of the magnetic moment of a superconductor in an inhomogeneous magnetic field equalizes to its gravity accurately. Because the pinning effect, the magnetic moment of the imperfect type-II superconductor is of diamagnetism or paramagnetism as the magnetic field’s change, so the superconductor may appear to be suspended over a magnetic gorge, or flied below the magnetic gorge. superconducting magnetic levitation; superconducting magnetic flying; magnetic moment; pinning effect; inhomogeneous magnetic field 2015-09-02; 2015-11-19 路峻岭(1946—),男,河北南宫人,清华大学物理系教授,主要从事大学物理教学和传感器敏感元件物理学研究工作. O 511.9 A 1000- 0712(2016)06- 0020- 09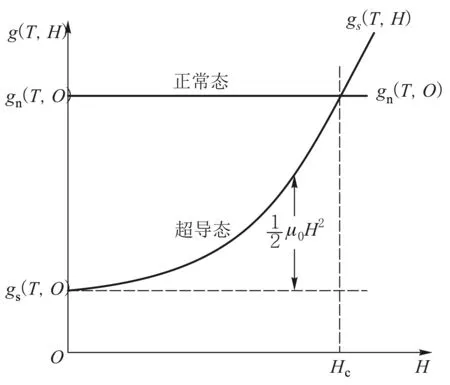
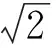
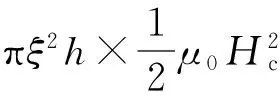
3 小结
