弹体斜侵彻硬介质目标的临界跳弹评估方法

段建，王可慧，周刚，李明，戴湘晖，李虎伟

（西北核技术研究所，陕西西安710024）

弹体斜侵彻硬介质目标的临界跳弹评估方法

段建，王可慧，周刚，李明，戴湘晖，李虎伟

（西北核技术研究所，陕西西安710024）

弹体斜侵彻硬介质目标过程将发生弹道偏转，甚至发生跳弹。弹体一旦跳弹，使弹体侵入不到目标内部，从而不能对目标形成有效打击。为保证弹体能够有效侵彻目标，需要对弹体侵彻目标的临界跳弹角度进行预测，给出弹体不发生跳弹的角度范围。为此，对弹体斜侵彻硬介质目标的跳弹进行研究，建立了预测弹体斜侵彻目标的跳弹分析评估方法。运用该方法对弹体分别侵彻抗压强度为30MPa和60MPa的钢筋混凝土的临界跳弹角度进行计算，并与实验结果进行了对比。结果表明，该方法能比较准确地分析和评估弹体的跳弹角度。

兵器科学与技术；战斗部；评估方法；斜侵彻；弹道偏转；临界跳弹角度

0 引言

在实际作战中，由于载体作用方式、目标表层特性、弹体的气动性能以及末端制导等因素的影响，战斗部在撞击目标时将带有一定的倾角和攻角，带有倾角和攻角的弹体侵彻称之为斜侵彻［1-2］。不同于正侵彻，由于斜侵彻过程中靶板对弹体阻力的不对称影响，导致弹体在侵彻过程将发生弹道偏转，甚至发生跳弹。

对于钻地战斗部，其有效作战模式是贯穿防护层介质，侵入目标结构内部爆炸，依靠爆炸产生的冲击波和破片等对其周围目标进行破坏和毁伤。弹体在侵彻过程中一旦发生跳弹，就失去了对目标的侵彻功能，使弹体侵入不到目标内部，从而不能对目标形成有效打击。因此，为保证战斗部能够有效侵彻目标，达到预定的作战毁伤目的，需要对弹体侵彻目标的临界跳弹角度（文中的跳弹角度指倾角角度）进行预测，给出弹体不发生跳弹的角度范围。

本文基于理论和经验的方法，开展了弹体斜侵彻目标性能研究，建立了预测弹体斜侵彻目标跳弹的分析评估方法。采用该方法，对弹体侵彻钢筋混凝土的跳弹进行了计算，给出了弹体的临界跳弹角度。进行了弹体侵彻钢筋混凝土的临界跳弹实验，分析了弹体的临界跳弹角度，并对计算结果和实验结果进行了对比分析。

1 弹体斜侵彻过程分析

1.1弹体斜侵彻运动学方程

为了研究方便，在弹体射平面内建立如图1所示的两组动坐标系。一组是以弹体质心O为原点，沿弹轴方向和垂直于弹轴方向建立Oxy坐标系；另一组也是以弹体质心O为原点，沿平行于靶表面方向和垂直于靶表面方向建立Ox′y′坐标系。

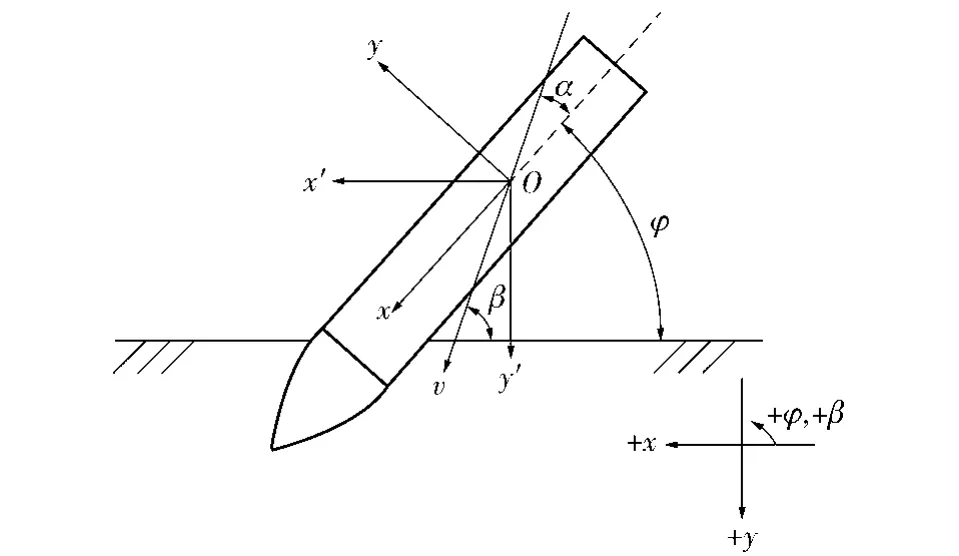
图1　弹-靶坐标系Fig.1 Coordinate systems of projectile-target

图1中:δ为攻角，即弹体速度方向与弹体轴线的夹角，沿弹轴方向，顺时针为正；β为撞击角，即弹体速度方向与靶面的夹角，其对应的余角为倾角，定义为弹体速度方向与靶面法线的夹角；φ为姿态角，即弹体轴线与靶面的夹角。

为使问题研究得到简化，作如下假设:

1）不计弹体侵彻过程变形，假定弹体为刚体。

2）弹体射平面在侵彻过程中方位不变，攻角和撞击角始终在射平面内。

3）不考虑弹体绕弹轴旋转对射平面及攻角和撞击角的影响。

4）侵彻过程中弹体的受力只有弹体的轴力、由攻角引起的横向力及由撞击角引起的横向力。

根据上述假设，建立弹体在靶目标介质中的运动微分方程，确定弹体侵彻规律。设弹体的质量为m，绕垂直于射平面的质心轴转动惯量为Jc，弹体沿x方向和y方向的受力分别为Fx和Fy.则在t时刻，x方向和y方向的加速度分别为

在t+Δt时刻，x和y方向的速度分别为

式中:vx（t）=v（t）cosδ，vy（t）=-v（t）sinδ.

在t+Δt时刻，x和y方向的位移分别为

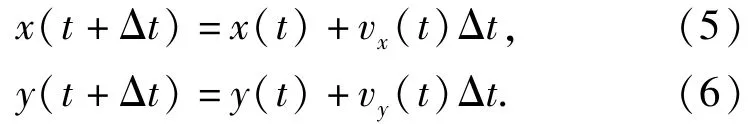
在Ox′y′坐标系中的各参量可通过坐标变换相应地求出。

在t时刻，弹体绕质心运动的角加速度为

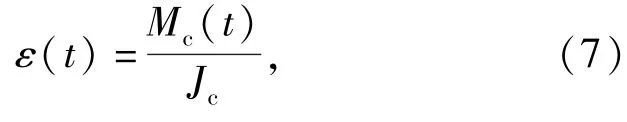
式中:Mc为作用在弹体质心力矩（N·m）；Jc为弹体绕质心转动惯量（kg·m2）。

在t+Δt时刻，弹体的角速度为

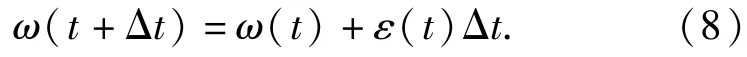
在t+Δt时刻，弹体的姿态角为

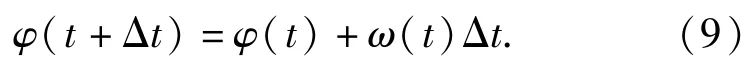
在t+Δt时刻，弹体的撞击角为

在任一时刻有

则在t+Δt时刻，弹体的攻角为

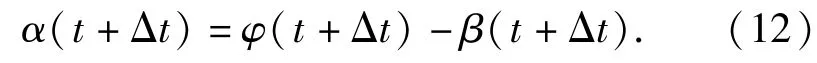
根据弹体质心的运动方程，可得到弹体头部顶点的运动方程，进而分析弹体在目标内的运动弹道轨迹:

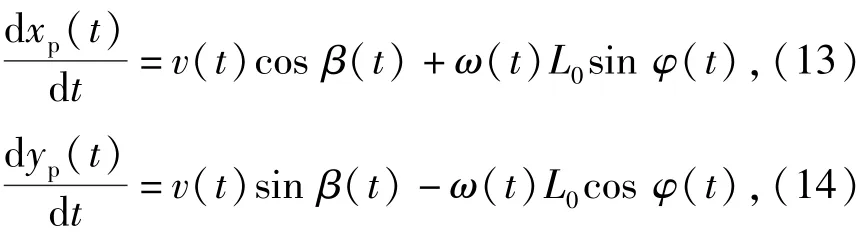
式中:xp（t）和yp（t）分别为t时刻弹体头部顶点运动的水平和竖直位移；v（t）为弹体的运动速度；L0为弹体顶点到质心的长度；对应的最大yp为弹体侵彻深度。

基于上述弹体运动规律，如果给出侵彻过程中弹体的受力情况，可对弹体侵彻速度、侵彻过载、侵彻角度随时间变化关系以及侵彻弹道等参数进行计算和分析。

1.2弹体侵彻过程受力分析

在斜侵彻过程中，弹体受力包括弹体的轴力和横向力。弹体的横向力有两种，即攻角引起的横向力和撞击角引起的横向力。为计算方便，假定弹体完全侵入每一层介质时的轴力不变，且由攻角和撞击角引起的横向力与弹体受到的最大轴力呈正比。

1.2.1弹体轴力计算

弹体轴力可以根据Young经验方程计算。Young方程［3-5］是由美国圣地亚实验室的Young在3000多次实验的基础上统计分析得到、用来预估钻地弹侵彻深度的经验方程。Young方程形式如下:

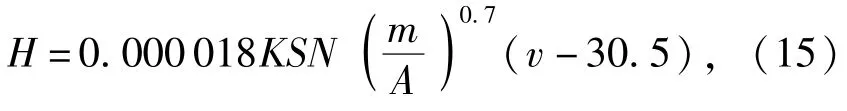
式中:H为侵彻深度（m）；m为弹体质量（kg）；v为侵彻速度（m/s）；A为弹体的横截面面积（m2）；S为可侵彻性指标；N为弹头形状影响系数；K为弹体质量修正系数。

通过Young方程计算弹体侵彻单层目标介质深度H，用a=v2/2H计算弹体侵彻目标介质过程的平均过载。假定弹体侵彻单层目标介质的最大轴力为常量，然后根据F=ma得到弹体最大轴力:

式中:FA为弹体完全侵入靶板受到的最大轴力。

在进行轴力计算时，需要考虑如下情况:

1）当弹头进入靶板时，弹体轴力随弹头进入靶板体积的增加而增加。当弹体头部完全侵入靶体内时，弹体轴力达到最大值FA，且保持不变。

2）当弹尖穿透硬介质目标进入空气或软介质目标内部时，由于靶板背面的层裂效应将减缓自由面的应力，从而降低弹体瞬间轴向过载，作用在弹体上的轴力将降低。计算弹体轴力时，需要考虑靶板背面层裂效应的影响。

3）对于弹体侵彻薄靶目标情况，在弹体头部还未完全进入靶目标内部，弹尖就已穿出目标，这就意味着弹体轴力不会达到最大值FA.

因此，弹体侵彻过程的瞬时轴力用（17）式计算:

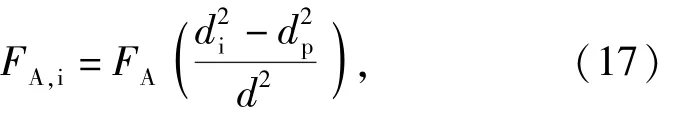
式中:FA，i为弹体侵彻靶板的瞬时轴力；di为侵入靶板内的最大弹头直径，弹头完全侵入靶体时di=d，d为弹体直径；dp为穿出靶板的最大弹头直径，弹头完全穿出靶体时dp=d，此时对应的di=d.

1.2.2弹体横向力计算

1）攻角引起的横向力

攻角引起的横向力计算如图2所示。

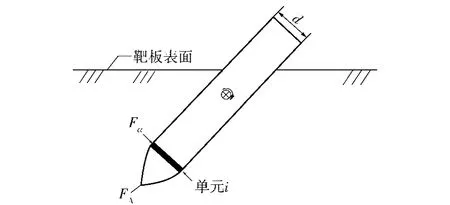
图2　作用在单元i由攻角引起的横向力计算示意图Fig.2 Lateral force on element i caused by angle of attack

在弹体撞击靶板瞬间，弹体的角速度可以忽略不计，此时弹体每一单元i的攻角相同。随着弹体进一步侵彻，导致弹体每一单元i的攻角不同，不能忽略弹体角速度。由于攻角的存在，与混凝土接触的弹体每一单元i将产生一个横向力。假定由攻角引起的横向力正比于弹体最大轴力与攻角的乘积，则弹体单元i由瞬时攻角引起的横向力可通过（18）式计算［6-7］:

式中:Fδ，i为单元i由攻角引起的横向力（N）；ε为成坑效应因子；ε′为层裂效应因子；As，i为弹体单元i的环向面积（m2）；vL，i为单元i的横向速度（m/s）；v为弹体瞬时侵彻速度（m/s）；kδ为攻角载荷系数。

ε描述了弹体撞靶成坑效应。当弹头侵入到硬目标介质时，弹体的撞击将在目标侵彻位置形成一个漏斗形弹坑。根据对大量试验测试结果分析，在混凝土靶板上形成的漏斗形弹坑深度约为弹体直径的2.5倍，大于2.5倍弹径的为弹体侵彻弹洞。在空气/靶板接触面，弹体侵彻靶板瞬间，弹体单元受到由攻角产生的横向载荷最小；当弹体侵彻到2.5倍弹径深度处时，与靶板接触的弹体单元受到的由攻角产生的横向载荷达到最大。同样，ε′描述了弹体穿出靶板的背面成坑效应，即靶板背面的层裂效应。由于弹体穿出靶板时，弹体接近靶板自由面，此时靶板背面的层裂效应降低了弹体侵彻阻力。大量试验结果表明，混凝土靶板的背面层裂成坑深度约为2倍弹径。

弹体在撞击靶板之前，ε取最小值0，即弹体侵彻靶板之前由攻角产生的横向力为0；在弹体侵入到2.5倍弹径深度处时，ε取最大值1.0；假定弹体从侵彻目标到侵入目标内2.5倍弹径深度处时，ε值呈线性递增。同样，在弹体完全穿过目标之后，ε取最小值0；在弹体侵入到距目标底部自由面2倍弹径深度处时，ε取最大值1.0；假定弹体从距目标底部自由面2倍弹径深度处到弹头穿透底部自由面，ε′值呈线性递减。根据上述分析，得到ε和ε′的计算表达式:

式中:h为靶板的厚度。

2）撞击角引起的横向力

撞击角引起的横向力计算如图3所示。撞击角引起的横向力主要是由于弹头位置上下压力不同产生的，因此横向力仅作用在弹体头部。对于正侵彻情况（姿态角为90°），弹头每侧受到的压力相同，撞击角引起的横向力为0.当姿态角不为90°时，侵彻过程中弹体头部靶板一侧的压力大于另一侧的压力，因此就在弹头部分产生了由撞击角引起的横向力。通过姿态角φ对撞击角产生的横向力进行计算。该横向力与弹头距靶板自由面的距离有关。当该距离大于某一值时，靶板自由面对弹头的作用可忽略不计，弹头位置上下压力相同。此时，撞击角引起的横向力为0.撞击角引起的横向力Fβ可用（21）式计算:

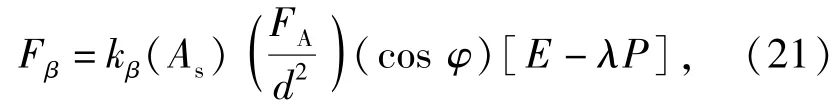
式中:Fβ为撞击角产生的横向力（N）；φ为姿态角（°）；Ε为描述弹头距靶板正面的位置函数；P为描述弹头距靶板背面的位置函数；λ为修正P的位置函数；As为进入靶板内的弹头环向面积（m2）；kβ为撞击角载荷系数。

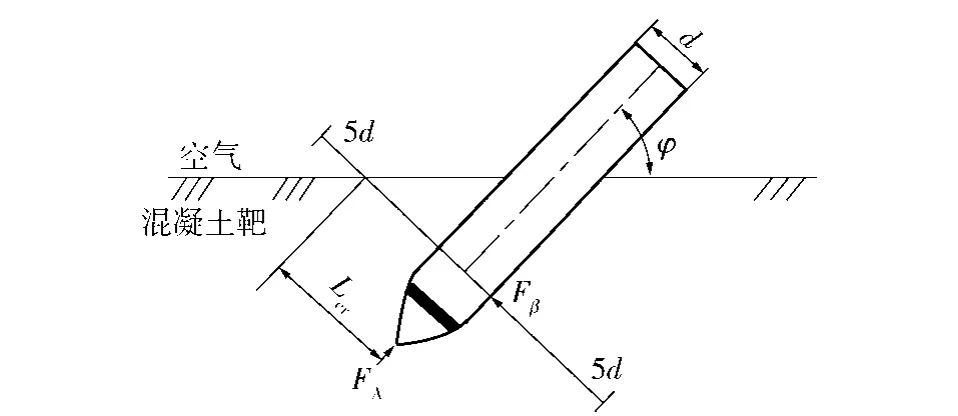
图3　由撞击角引起的横向力计算示意图Fig.3 Lateral force caused by impact angle

由于横向力与弹头距靶板自由面的距离有关，自由面对弹体侵彻的影响取决于弹体至自由面的距离。如图3所示，取Lcr/d作为表征靶面至弹体自由面距离的无量纲值。当时，弹体将受到由撞击角引起的横向载荷。而当时，由撞击角引起的作用在弹体的横向载荷为0.定义为自由面效应距离判别阈值与目标类型有关。对于钢筋混凝土，取当弹头侵彻深度达到5倍弹径时，可忽略靶板自由面效应的影响，此时撞击角引起的横向力为0.

Ε作为描述弹头距靶板正面自由面的位置函数，是根据弹体头部距离靶板正面自由面的接近程度量化和确定的。当弹头刚开始侵彻靶板时，Ε取最大值1；当弹头侵彻到距靶板正面自由面为5倍弹径时，Ε取最小值0.假定弹头从侵彻开始至侵彻到距正面自由面5倍弹径处，Ε值呈线性递减。Ε的表达式如下:

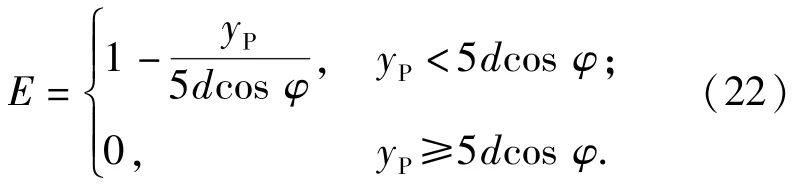
同样，P作为描述弹头距靶板背面自由面的位置函数，与Ε的功能一样，它是根据弹头距离目标背面自由面的接近程度量化和确定的。当弹头侵彻到距靶板背面自由面为5倍弹径的深度处时，P取最小值0；当弹头完全穿出靶板时，P取最大值1.假定弹头从距靶板背面自由面5倍弹径处到完全穿出靶板，P值呈线性递增，则P值可用（23）式计算:

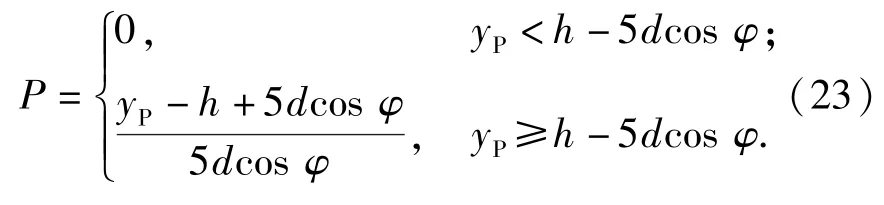
λ是修正P的位置函数。λ根据弹头在靶板内的位置确定，其表达式如下:

1.3求解过程

首先求解作用在弹体上的轴力、由攻角和撞击角产生的横向力以及由横向力引起的绕质心力矩。将求出的力和力矩代入弹体运动学方程，可得到弹体绕质心的转动方程和弹体质心的运动方程。然后，采用中心差分法对弹体侵彻过程的运动方程进行数值求解，从而求出弹体侵彻过程中速度、过载、角度以及侵彻弹道等参量随时间的变化关系。

对作用在弹体上的力的计算是:采用离散法计算侵入弹体离散单元的横向力，再进行横向力的求和计算。侵入靶板的弹体范围可以根据侵彻深度以及di、dp的大小来确定，然后沿弹体轴向进行离散处理，再依次循环求解各个离散片段的受力结果。根据已获得的di和dp状态值直接求解弹体侵彻过程受到的轴力。

2 弹体临界跳弹计算

在弹体侵彻过程中，如果弹体姿态角减小到0°时，弹体轴线与靶面平行，弹体对靶板厚度方向不再具备侵彻能力，认为弹体发生跳弹。因此，弹体发生跳弹的条件为侵彻过程中弹体姿态角变为0°.

针对弹体斜侵彻过程的基本动力学运动规律和受力方程，编写了计算程序。在不考虑攻角的情况下，根据侵彻过程的弹体跳弹条件，采用该计算程序对弹体在260～420m/s速度和不同倾角下分别侵彻抗压强度为30MPa和60MPa的钢筋混凝土过程进行了计算，分析了弹体的临界跳弹角度。

计算所用的弹、靶参数如下:

弹体:质量3.7kg，直径0.05m，长度0.42m，弹头形状系数4.5，卵形弹头的长度0.1m，质心距离弹头的长度0.22m，绕质心的转动惯量0.05kg·m2.

靶板:抗压强度为30MPa和60MPa的钢筋混凝土靶板，体积配筋率0.2%，靶板厚度2m.

根据上述弹、靶条件，对弹体在260m/s、300m/s、340m/s、380m/s和420m/s不同速度下侵彻钢筋混凝土的临界跳弹角度进行了计算，计算结果如表1所示。

表1　计算得到的弹体侵彻靶板临界跳弹角度Tab.1 Calculated results of critical ricochets of penetrators impacting targets

3 弹体侵彻钢筋混凝土的临界跳弹实验

根据上述弹、靶参数，设计了实验弹和混凝土靶板，采用130mm轻气炮进行了弹体在约260m/s、310m/s、340m/s、380m/s和420m/s不同速度下以不同倾角分别侵彻抗压强度为30MPa和60MPa的钢筋混凝土实验。

图4示出典型弹体撞靶临界跳弹实验图片。根据弹体侵彻实验结果及弹道情况，对弹体分别侵彻抗压强度为30MPa和60MPa的钢筋混凝土的临界跳弹情况进行了分析，得到弹体在不同速度下的临界跳弹角度，如表2所示。

图4　弹丸以257m/s速度、36°倾角侵彻抗压强度为60MPa的钢筋混凝土时的跳弹Fig.4 Photograph of projectile impacting concrete target at 257 m/s and 36°

4 计算与实验结果对比分析

将弹体临界跳弹角度计算结果与实验结果进行对比，如图5所示。

对比表明，计算结果与实验结果给出的弹体临界跳弹角度随速度变化的趋势一致。弹体侵彻同一强度靶板时，随着侵彻速度的增加，弹体的临界跳弹角度变大，且弹体临界跳弹角度随速度增加而增大的变化趋势逐渐变缓。该变化趋势说明，随速度的增加，弹体临界跳弹角度存在上限。理论上，在不考虑弹体结构强度的情况下，其临界跳弹角度上限为90°.

弹体在同一速度下侵彻不同强度钢筋混凝土靶板时，随着靶板强度的增加，弹体的临界跳弹角度变小。

此外，对弹体分别侵彻抗压强度为30MPa和60MPa的钢筋混凝土的临界跳弹角度计算值与实验值进行了分析，其相对偏差不超过6%，计算结果与实验结果有较好的一致性。

表2　实验得到的弹体侵彻靶板临界跳弹角度Tab.2 Experimental results of critical ricochets of projectiles impacting targets

图5　弹体临界跳弹角度与速度关系曲线对比Fig.5 Critical ricochet angle vs.velocity

5 结论

基于理论与经验的方法，结合弹体侵彻过程的运动规律及弹体受力方程，建立了预测弹体斜侵彻目标跳弹的分析评估方法。

开展了弹体在260～420m/s速度下分别侵彻抗压强度为30MPa和60MPa的钢筋混凝土靶板时临界跳弹的理论计算和实验研究，分析了弹体的临界跳弹角度。

对计算结果与实验结果进行了对比分析。结果表明，弹体侵彻同一强度靶板时，随着侵彻速度的增加，弹体的临界跳弹角度变大，且弹体临界跳弹角度随速度增加而增大的变化趋势逐渐变缓。弹体在同一速度下侵彻不同强度钢筋混凝土靶板时，随着靶板强度的增加，弹体的临界跳弹角度变小。

计算结果与实验结果一致性较好，表明建立的弹体斜侵彻硬介质目标的临界跳弹评估方法能够有效预测弹体斜侵彻目标过程的临界跳弹角度。

（References）

［1］ 初哲.弹体非正侵彻混凝土研究［D］.北京:北京理工大学，2006. CHU Zhe.Study of non-normal penetration into concrete of projectile［D］.Beijing:Beijing Institute of Technology，2006.（in Chinese）

［2］ Goldsmith W.Non-ideal projectile impact on targets［J］.International Journal of Impact Engineering，1999，22（2）:95-395.

［3］ Young C W.Depth prediction for earth-penetrating projectiles［J］.Journal of the Soil Mechanics and Foundations Division，1969，95（3）:803-817.

［4］ Young C W.Equation for predicting earth penetration by projectiles:an update，SAND-88-0013［R］.Albuquerque，NM:Sandia National Laboratories，1988.

［5］ Young C W.Penetration equations，SAND-97-2426［R］.Albuquerque，NM:Sandia National Laboratories，1997.

［6］ Young C W.A simplified analytical model of penetration with lateral loading（SAMPLL）-an update，SAND 91-2175［R］.Albuquerque，NM:Sandia National Laboratories，1992.

［7］ Young C W.A simplified analytical model of penetration with lateral loading user's guide，SAND98-0978［R］.Albuquerque，NM:Sandia National Laboratories，1998.

Evaluation Method for Critical Ricochet of Projectile Obliquely Penetrating Hard Target

DUAN Jian，WANG Ke-hui，ZHOU Gang，LI Ming，DAI Xiang-hui，LI Hu-wei
（Northwest Institute of Nuclear Technology，Xi'an 710024，Shaanxi，China）

The ballistic trajectory of a projectile may deflect or it ricochets off a target when the projectile penetrates a hard target obliquely.Once the projectile ricochets off a hard target，it cannot perforate into the target，which cannot bring effective damage to the target.In order to ensure that the projectile penetrate the hard target effectively，the critical ricochet angles of projectile impacting the hard target need to be predicted，and the range of angles of that the projectile does not ricochet is given.Consequently，the ricochet of projectile penetrating a hard target obliquely is studied，and then an evaluation method of predicting the critical ricochet of projectile is proposed.The critical ricochet angles of projectiles penetrating the reinforced concretes with compressive strength of 30 MPa and 60 MPa are calculated using the proposed method，respectively，and the calculated results are compared with the experimental results.The results show that the evaluation method can be used to analyze and evaluate the ricochet of projectile precisely.

ordnance science and technology；warhead；evaluation method；oblique penetration；ballistic deflection；critical ricochet angle

TJ012.4

A

1000-1093（2016）08-1395-06

10.3969/j.issn.1000-1093.2016.08.008

2015-08-24

段建（1979—），男，副研究员。E-mail:duanjian@nint.ac.cn