非恒定环境下基于载荷谱的导弹部件寿命预测

王浩伟，滕克难，奚文骏

（1.海军航空工程学院兵器科学与技术系，山东烟台264001；2.海军航空工程学院训练部，山东烟台264001）

非恒定环境下基于载荷谱的导弹部件寿命预测

王浩伟1，滕克难2，奚文骏1

（1.海军航空工程学院兵器科学与技术系，山东烟台264001；2.海军航空工程学院训练部，山东烟台264001）

为了解决某导弹部件在非恒定贮存环境下的寿命预测问题，提出了一种基于环境载荷谱的预测方法。分别利用Normal、Gamma分布对温度、湿度载荷谱建模；采用三参数Weibull分布拟合产品的失效时间，进而通过加速因子不变原则推导与环境相关的模型参数，在此基础上利用简化的广义Eyring模型建立时变环境与寿命模型之间的联系。案例应用验证了所提方法的有效性，结果表明此方法比传统的基于环境平均值的预测方法降低了预测误差。

兵器科学与技术；寿命预测；非恒定环境；载荷谱；三参数Weibull分布；加速因子不变原则

0 引言

准确预测出导弹部件的寿命对高效开展预防性维修、提高导弹的作战使用效能具有重要意义。装备的寿命是和所受的环境载荷及工作载荷紧密相关的，在我国这种南北、东西跨度较大的陆疆和海疆上，由于温度、湿度等环境载荷相差较大，不同地域的相同型号装备往往表现出不同的寿命特性［1］，然而生产厂家一般只给出装备在标准使用、贮存环境下的寿命，难以指导装备的预防性维修工作。而导弹属于“长期贮存、一次使用”的武器装备，在寿命周期内会循环执行库房贮存、运输、阵地值班等任务。导弹执行阵地值班任务时，导弹的环境载荷受自然环境的影响呈现出非恒定、周期性变化的特点，其寿命与标准使用、贮存环境下相比具有较大差异，因此根据实际贮存环境预测导弹部件的寿命具有较强的工程研究价值。

目前已有不少学者开始探讨、研究非恒定环境下的寿命预测方法。Gebraeel等［2］提出了一种融合部件个体退化数据、部件总体退化特征以及实时环境信息的随机模型，并采用Bayesian更新的方式预测轴承在时变负载与转速下的剩余寿命。刘震宇等［3］利用Gamma分布描述导弹发射箱内的温度变化，进而采用比例风险模型预测导弹部件在非恒定温度下的寿命。Bian等［4-5］在利用性能退化数据预测产品剩余寿命时也考虑了时变环境因素的影响，他们利用Bayesian方法将退化数据与环境数据进行融合。Jin等［6］在预测动量轮寿命时采用Wiener过程对轴承润滑油的损耗进行建模，其中利用带有协变量的漂移参数描述非恒定温度对润滑油损耗的影响。Liao等［7］假定Wiener过程的漂移参数与环境协变量有关而扩散参数与协变量无关，研究了非恒定环境下个体剩余寿命预测方法。肖坤等［8］开展了某引信用O型橡胶密封圈的加速退化试验，为了准确推出产品在实际贮存温度下的可靠度，将库房温度按季节划分为4段进行可靠度折算。

非恒定环境下的寿命预测方法主要有两方面关键内容:一是如何对预测对象的非恒定环境进行载荷谱建模，然而目前的大部分研究工作只考虑了单一环境协变量；二是如何将环境协变量融入到寿命预测模型，基于比例风险模型的建模方法虽然可解决这一问题，但复杂的参数估计过程降低了此方法的可用性［9］。为了准确预测非恒定贮存环境下的某导弹部件寿命，本文考虑了温度、湿度两种非恒定环境因素对产品寿命的影响，利用加速因子不变原则将环境协变量融入寿命预测模型，以温度、湿度和贮存时间为输入量进行寿命预测。

1 温度、湿度载荷谱建模

导弹是较为典型的机电一体化产品，研究表明温度、湿度是影响导弹寿命的两个最主要因素并且持续作用于导弹的整个寿命周期［10-11］。导弹大部分时间处于库房贮存状态，由于库房中的温度、湿度变化很小并且导弹置于储运发射箱内，库房贮存环境可认为是恒定的。当导弹在阵地值班时，自然环境的变化使得导弹贮存环境非恒定，主要体现在气温、湿度的日变化和年度内的季节变化。某导弹在每年中执行值班任务的月份相同，因为贮存环境在年度间的变化可忽略不计，所以只对一年中的温度、湿度值进行统计分析即可描述出非恒定贮存环境。导弹储运发射箱内部安装了温度、湿度传感器，每3h采集一次温度、湿度值，一年内共采集了2920组数据，通过如下步骤建立温度载荷谱:

1）以0℃为中心，长度为2℃建立温度区间，例如各温度区间为［-3℃，-1℃］、［-1℃，1℃］、［1℃，3℃］等；

2）统计一年中的温度采集值落在各温度区间内的次数，如果温度值是奇数，则相关两个温度区间的计数各增加0.5次；

3）将温度采集值落在各温度区间的次数除以一年中的总采集数2920，得出温度采集值落在各温度区间的频次。

将相对湿度区间取为［0，2%］、［2%，4%］等，利用类似的方法也可建立湿度载荷谱。图1、图2分别为导弹的温度载荷谱和湿度载荷谱。

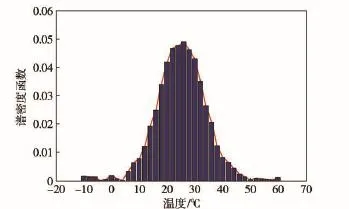
图1　温度载荷谱Fig.1 Load spectrum of temperature

由于温度载荷谱形状左右对称，故采用正态分布进行拟合；由于相对湿度为非负值，并且湿度载荷谱呈现单峰、左倾的特点，所以考虑利用Gamma分布对湿度载荷谱拟合。温度载荷谱的密度函数为

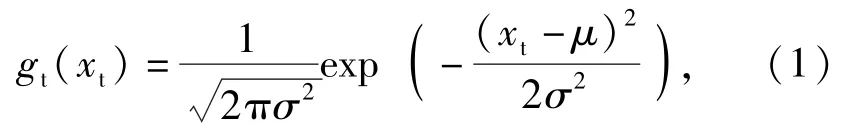
式中:xt为温度变量；μ为均值；σ为标准差。

湿度载荷谱密度函数为

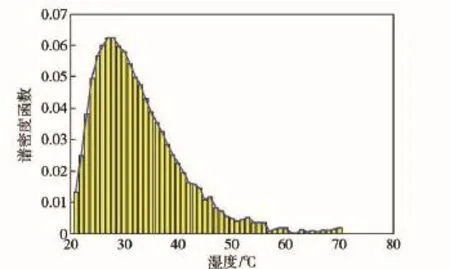
图2　湿度载荷谱Fig.2 Load spectrum of relative humidity

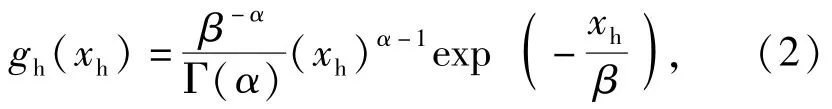
式中:xh为湿度变量；δ、β分别为形状参数和尺度参数。假定温度和湿度相互独立，环境载荷谱的联合密度函数为

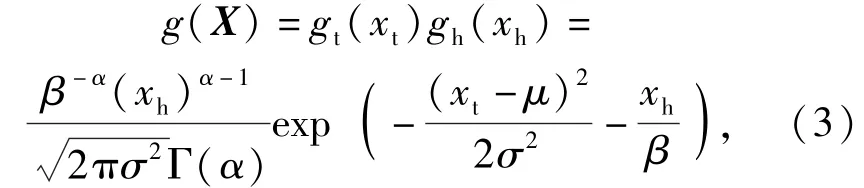
式中:X=（xt，xh）为环境向量。

2 基于载荷谱的可靠性模型

文献［3］采用比例风险模型建立环境X与失效率函数之间的关系，设标准环境为X0，产品在标准环境下的失效率为λ0（t0|X0），则产品在加速环境

Xa下的失效率为

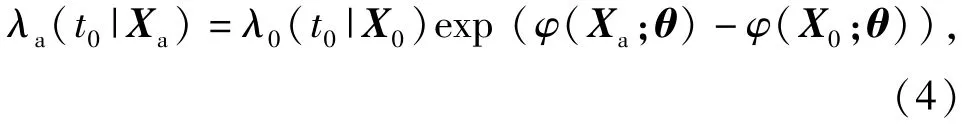
式中:φ（·，θ）为环境协变量函数；θ为待定系数向量；exp（φ（Xa；θ）-φ（X0；θ））与t0无关。

文献［3］中的方法需要确定出产品的失效率函数，但是很多情况下（例如利用随机过程模型进行产品性能退化建模时）的失效率函数比较复杂，而且待定系数向量θ难以估计。为了克服以上不足，本文引入加速因子不变原则［12-14］进一步推导环境X与失效率函数中的哪些参数有关。

假设Ra（ta）、R0（t0）分别表示产品在环境Xa和环境X0下的可靠度，当Ra（ta）=R0（t0）时，可将环境Xa相当于环境X0的加速因子定义为Ka，0= t0/ta.周源泉等［12］推导出了加速因子的一个等效表达式为

加速因子不变原则是指Ka，0应是一个与时间t无关并且只由φ（Xa；θ）、φ（X0；θ）确定的常数，否则Ka，0就失去了工程应用性。值得注意的是比例风险模型也要求产品在Sa和S0下的失效率之比为与时间t无关的常数［15］，如（4）式中λa（t0|Xa）/λ0（t0| X0）=exp（φ（Xa；θ）-φ（X0；θ））=C，C与Ka，0为函数关系，当产品失效时间服从指数分布时C= Ka，0.

某导弹部件为机电产品，三参数Weibull分布可较好拟合此类产品的故障时间［16］，则可靠度函数为

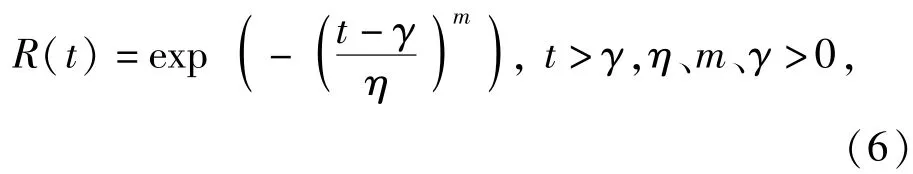
式中:γ、η、m分别为位置参数、尺度参数和形状参数。由（6）式可得产品的失效率函数为

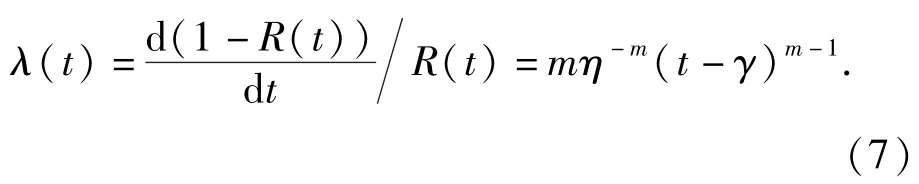
将（7）式代入（5）式，可得

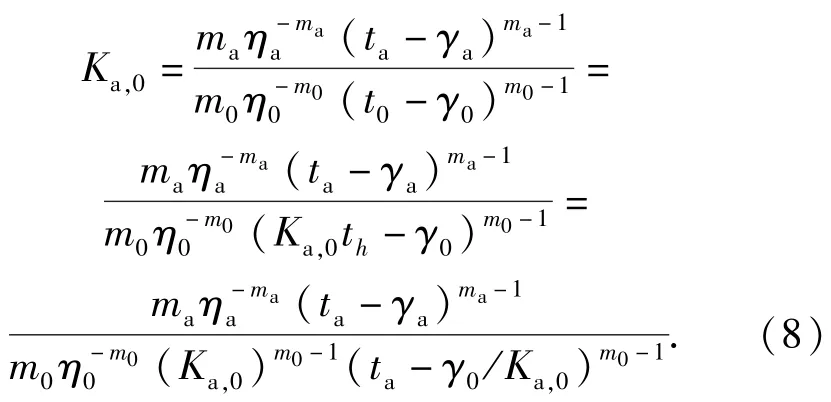
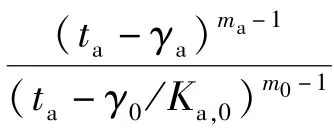
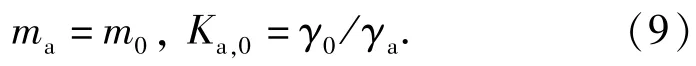
将（9）式代入（8）式，推导得

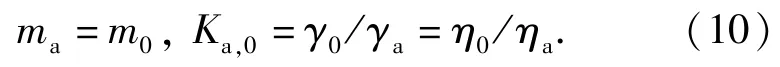
由于γ、η在Xa与X0下发生了变化，而m在Xa与X0下保持不变。由此可知，γ、η与X有关而m与X无关。γ、η与X之间的关系可利用加速模型进行描述，简化的广义Eyring模型和Peck模型都可以作为温度、湿度双应力加速模型［17-18］。假定加速模型为简化的广义Eyring模型，则γ可由X表示为

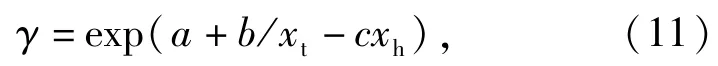
式中:a、b、c为待定系数。为了满足（10）式中的关系式γ0/γa=η0/ηa，η可由X表示为

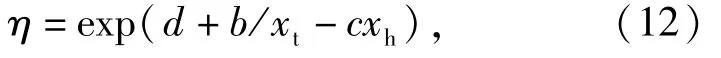
则产品在环境X=（xt，xh）下的条件概率密度函数f（t|xt，xh）和条件可靠度函数R（t|xt，xh）为

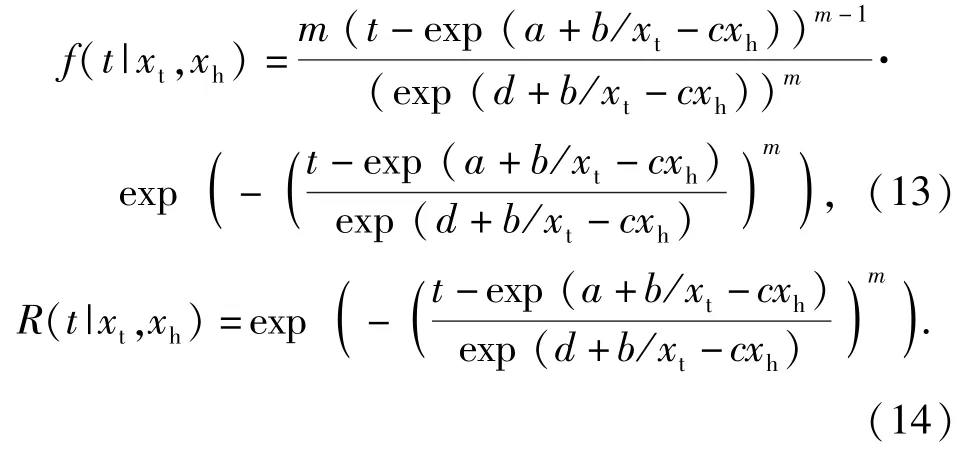
由R（t|xt，xh）及（1）式、（2）式推导出无条件可靠度函数R（t）为

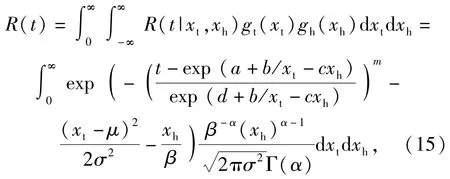
式中:μ、σ、δ、β、m、a、b、c、d为待定系数。

3 参数估计与寿命预测

首先对环境载荷谱密度函数的待定系数μ、σ、δ、β进行估计。根据（1）式建立如下似然方程:

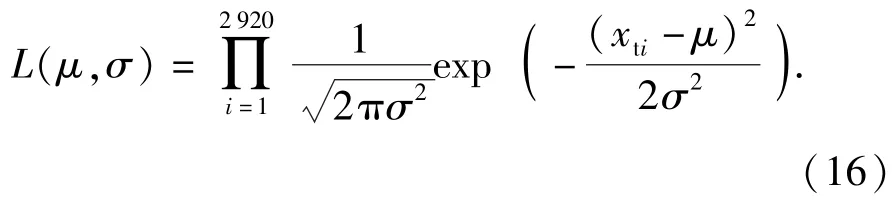
将2920个温度采集值xti代入（16）式可估计出根据（2）式建立如下似然方程估计出

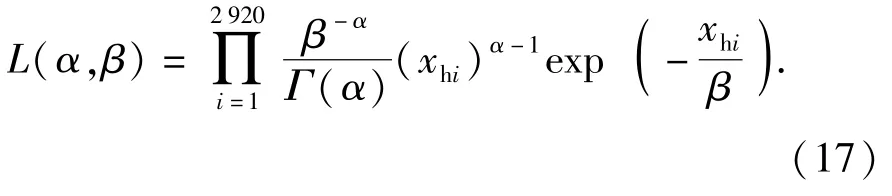
然后对条件可靠度函数R（t|xt，xh）中的待定系数m、a、b、c、d进行估计，方法有两种:一是根据工程经验对各待定系数赋值；二是开展产品的温度、湿度双应力加速寿命试验，利用试验数据进行更为准确的估计。假定导弹部组件的加速寿命试验数据为（ξj，k，δj，k，xt，k，xh，k），ξj，k代表第k组加速应力下第j个导弹部件的故障时间信息，δj，k为指示参数，δj，k=1表示ξj，k为故障时间，δj，k=0表示ξj，k为右截尾时间，xt，k、xh，k分别为第k组加速应力的温度值和相对湿度值，其中:k=1，2，…q；j=1，2，…nq.根据加速试验数据，建立如下极大似然方程:

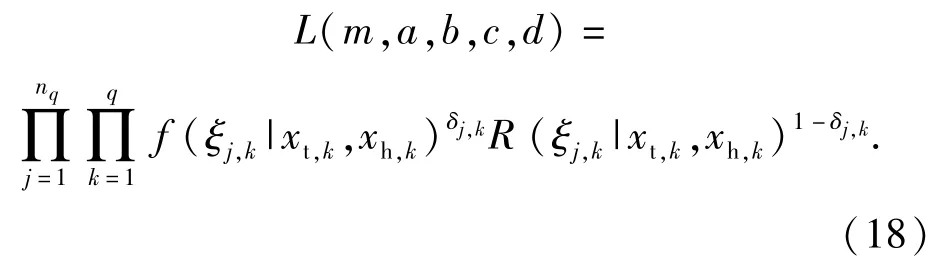
最后将系数估计值代入（15）式确定出非恒定环境下的可靠度函数并进一步利用预测导弹部件的可靠寿命、平均寿命等。

4 案例应用

某导弹部件已经开展了温度、湿度双应力加速寿命试验，24个样品被平均分配到4组加速应力下进行试验，具体试验数据如表1所示。本节利用加速试验数据以及导弹在库房外贮存时的环境载荷谱信息，预测此导弹部件的寿命。

表1　加速试验数据Tab.1 Accelerated test data

将表1中的加速试验数据代入（18）式，采用简化的广义Eyring模型作为加速模型进行参数估计，解得将估计值代入（12）式可得产品的尺度参数η随温度xt和相对湿度xh的变化规律，如图3所示。

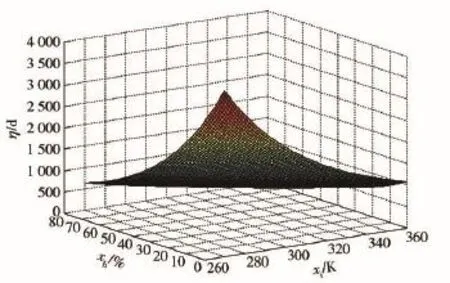
图3　尺度参数随温度、湿度的变化情况Fig.3 Scale parameter vs.temperature and relative humidity

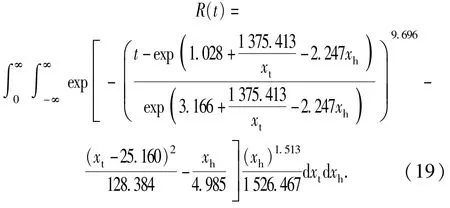
传统的预测方法将温度、湿度的平均值代入（14）式获取可靠度函数。根据温度、湿度载荷谱信息得利用传统方法获取的可靠度函数R*（t）为

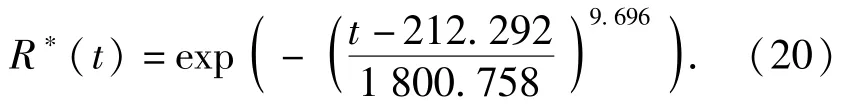
R⊙（t）为利用导弹部件的历史故障数据评估出的可靠度函数。图4展示了导弹部件的可靠度曲线，可见R（t）与R⊙（t）更为接近，证实了本文所提方法的有效性；而R*（t）与R⊙（t）明显不一致，说明利用环境平均值预测产品在非恒定环境下的寿命可能造成较大的误差。

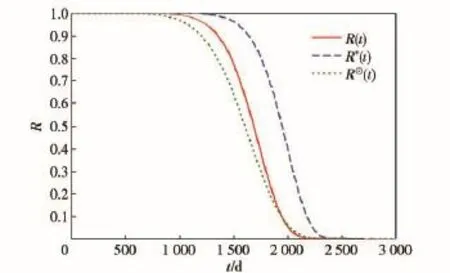
图4　导弹部件的可靠度曲线Fig.4 Reliability curves of missile component

5 结论

1）考虑了温度、湿度两种非恒定环境因素对产品寿命的影响，提出了建立温度、湿度载荷谱的方法，为其他非恒定环境载荷谱建模提供了有益借鉴。

2）利用加速因子不变原则可推导出寿命模型的哪些参数与环境协变量相关，为将环境协变量融入寿命模型提供了一种有效方法。

3）利用环境平均值预测产品在非恒定环境下寿命可能造成较大的预测误差，本文方法为预测产品在非恒定贮存环境下的寿命提供了一种更为有效的途径。

（References）

［1］ 张小丽，陈雪峰，李兵，等.机械重大装备寿命预测综述［J］.机械工程学报，2011，47（11）:100-116. ZHANG Xiao-li，CHEN Xue-feng，LI Bing，et al.Review of life prediction for mechanical major equipment［J］.Journal of Mechanical Engineering，2011，47（11）:100-116.（in Chinese）

［2］ Gebraeel N，Pan J.Prognostic degradation models for computing and updating residual life distributions in a time-varying environment［J］，IEEE Transactions on Reliability，2008，57（4）:539-550.

［3］ 刘震宇，马小兵，赵宇.非恒定温度场合弹上性能退化型部件贮存可靠性评估［J］.航空学报，2012，33（9）:1671-1678. LIU Zhen-yu，MA Xiao-bing，ZHAO Yu.Storage reliability assessment for missile component with degradation failure mode in a temperature varying environment［J］.Acta Aeronautica et Astronautica Sinica，2012，33（9）:1671-1678.（in Chinese）

［4］ Bian L，Gebraeel N.Stochastic methodology for prognostics under continuously varying environment profiles［J］.Statistical Analysis and Data Mining，2013，6（3）:260-270.

［5］ Bian L，Gebraeel N，Kharoufeh J P.Degradation modeling for real-time estimation of residual lifetimes in dynamic environments［J］.IIE Transactions，2015，47（5）:471-486.

［6］ Jin G，Matthews D，Fan Y，et al.Physics of failure-based degradation modeling and lifetime prediction of the momentum wheel in a dynamic covariate environment［J］.Engineering Failure Analysis，2013，28（3）:222-240.

［7］ Liao H，Tian Z.A framework for predicting the remaining useful life of a single unit under time-varying operating conditions［J］. IIE Transactions，2013，45（9）:964-980.

［8］ 肖坤，顾晓辉，彭琛.基于恒定应力加速退化试验的某引信用O型橡胶密封圈可靠性评估［J］.机械工程学报，2014，50（16）:62-69. XIAO Kun，GU Xiao-hui，PENG Chen.Reliability evaluation of the O-type rubber sealing ring for fuse based on constant stress accelerated degradation testing［J］.Journal of Mechanical Engineering，2014，50（16）:62-69.（in Chinese）

［9］ 洪东跑，赵宇，马小兵.基于比例风险模型的可靠性灵敏度分析［J］.宇航学报，2011，32（8）:1865-1870. HONG Dong-pao，ZHAO Yu，MA Xiao-bing.A proportional risk model-based reliability sensitivity analysis［J］.Journal of Asronautics，2011，32（8）:1865-1870.（in Chinese）

［10］ 王浩伟，奚文骏，冯玉光.基于退化失效与突发失效竞争的非恒定环境下基于载荷谱的导弹部件寿命预测导弹剩余寿命预测［J］.航空学报，2016，37（4）:1240-1248. WANG Hao-wei，XI Wen-jun，FENG Yu-guang.Remaining life prediction based on competing risks of degradation failure and traumatic failure for missile［J］.Acta Aeronautica et Astronautica Sinica，2016，37（4）:1240-1248.（in Chinese）

［11］ 张仕念，吴勋，颜诗源，等.贮存使用环境对导弹性能的影响［J］.装备环境工程，2014，11（5）:17-22. ZHANG Shi-nian，WU Xun，YAN Shi-yuan，et al.Influencing mechanism of storage/use environment on missile performance［J］.Equipment Environmental Engineering，2014，11（5）:17-22.（in Chinese）

［12］ 周源泉，翁朝曦，叶喜涛.论加速系数与失效机理不变的条件（Ⅰ）——寿命型随机变量的情况［J］.系统工程与电子技术，1996，18（1）:55-67. ZHOU Yuan-quan，WENG Chao-xi，YE Xi-tao.Study on accelerated factor and condition for constant failure mechanism［J］. System Engineering and Electronics，1996，18（1）:55-67.（in Chinese）

［13］ 徐廷学，王浩伟，张磊.恒定应力加速退化试验中避免伪寿命分布误指定的一种建模方法［J］.兵工学报，2014，35（12）:2098-2103. XU Ting-xue，WANG Hao-wei，ZHANG Lei.A reliability modeling approach to avoiding mis-specification of pseudo life distribution in CSADT［J］.Acta Armamentarii，2014，35（12）: 2098-2103.（in Chinese）

［14］ 王浩伟，徐廷学，赵建忠.融合加速退化和现场实测退化数据的剩余寿命预测方法［J］.航空学报，2014，35（12）: 3350-3357. WANG Hao-wei，XU Ting-xue，ZHAO Jian-zhong.Residual life prediction method fusing accelerated degradation and field degradation data［J］.Acta Aeronautica et Astronautica Sinica，2014，35（12）:3350-3357.（in Chinese）

［15］ 洪东跑，马小兵，赵宇.基于比例风险模型的可靠性综合评估［J］.系统工程与电子技术，2010，32（10）:2132-2135. HONG Dong-pao，MA Xiao-bing，ZHAO Yu.Integrated reliability assessment based on proportional risk model［J］.Systems Engineering and Electronics，2010，32（10）:2132-2135.（in Chinese）

［16］ 张祥坡，尚建忠，陈循，等.三参数Weibull分布竞争失效场合变应力加速寿命试验统计分析［J］.兵工学报，2013，34（12）:1603-1610. ZHANG Xiang-po，SHANG Jian-zhong，CHEN Xun，et al.Statistical inference of varying-stress accelerated life test with competing failures based on three-parameter Weibull distribution［J］. Acta Armamentarii，2013，34（12）:1603-1610.（in Chinese）

［17］ Escobar L A，Meeker W Q.A review of accelerated test models［J］.Statistical Science，2006，21（4）:552-577.

［18］ Park C，Padgett W J.Stochastic degradation models with several accelerating variables［J］.IEEE Transactions on Reliability，2006，55（2）:379-390.

［19］ Efron B.Better bootstrap confidence intervals［J］.Journal of A-merican Statistical Association，1987，82（397）:171-185.

［20］ Marks C E，Glen A G，Robinson M W，et al.Applying bootstrap methods to system reliability［J］.The American Statistician，2014，68（3）:174-180.

［21］ Ntzoufras I.Bayesian modeling using WinBUGS［M］.New York:John Wiley and Sons，2009.

［22］ Rigat F，Mira A.Parallel hierarchical sampling:a general-purpose interacting Markov chains Monte Carlo algorithm［J］.Computational Statistics&Data Analysis，2012，56（6）:1450-1467.

Load Spectra-based Lifetime Prediction for Missile Components under Varying Environment

WANG Hao-wei1，TENG Ke-nan2，XI Wen-jun1
（1.Department of Ordnance Science and Technology，Naval Aeronautical and Astronautical University，Yantai 264001，Shandong，China；2.Department of Training，Naval Aeronautical and Astronautical University，Yantai 264001，Shandong，China）

A forecasting method based on the environmental load spectra is proposed for predicting the lifetime of missile components under time-varying storage environment.Normal and Gamma distributions are used to model the load spectra for collected temperature and humidity data，respectively.A three-parameter Weibull distribution is utilized to fit the time of failure，then the parameters，which are dependent on environment，are determined using acceleration factor constant principle.Furthermore，a simplified generalized Eyring model is used to establish the relationship between the time-varying environment and the reliability model.A case study is provided to validate the effectiveness of the proposed method. The results show that the proposed method can be used to reduce the prediction error compared with the traditional prediction method that takes the average environment as varying environment.

ordnance science and technology；lifetime prediction；varying environment；load spectrum；three-parameter Weibull distribution；acceleration factor constant principle

TJ761.1；TB114.3

A

1000-1093（2016）08-1524-06

10.3969/j.issn.1000-1093.2016.08.026

2015-12-05

国家自然科学基金项目（51605487）

王浩伟（1981—），男，讲师，博士后。E-mail:13705355730@139.com