野战输油管线排空过程的气体与液体两相流瞬态模型

姜俊泽，张伟明，段纪淼，雍歧卫，蒋明

（后勤工程学院军事供油工程系，重庆401331）

野战输油管线排空过程的气体与液体两相流瞬态模型

姜俊泽，张伟明，段纪淼，雍歧卫，蒋明

（后勤工程学院军事供油工程系，重庆401331）

排空是野战输油管线的一项常规作业，为了提高排空作业的科学性和效率，建立了野战输油管线排空过程的瞬态模型，模型包括气体运动方程、液体运动方程以及相界面的耦合方程，并采用有限体积法对模型进行求解。在空压机排气压力和排气量给定的情况下，利用该模型可以计算出排空过程的管内各点压力、流量和持液率等参数。通过与实验参数对比，表明该模型计算精度较高，可以用于排空过程的管线运行参数预测，为排空设计和操作提供参考依据。

石油化学工程；野战输油管线；排空；两相流；参数；瞬态模型

0 引言

野战输油管线是地面铺设且用快装接头连接的一种输油管线系统，具有机动能力强、输油方向灵活等特点，是我军战时油料保障的主要手段。管线在清管、撤收或改输油品时需要将管内的油品排出，这一过程称为排空，也称为清管。气顶排空作为一种主要的排空方法，具有不受环境条件限制，不需要充足水源的优点。气顶排空有两种方法:一种是使用清管器，作为气体与液体（简称气液）隔离装置；一种是不加装清管器，气体直接作用于液体。不论使用哪种方法，管内都会形成气液两相流，发生相间的相互作用，同时伴随着管内压力的波动和流量的变化，目前有些学者对这一过程进行了研究，取得了一些成果，如Minami［1］建立了使用清管器的管线排空模型，模型将管线分为3个流动区域，即清管器上游和多相流区，清管器下游附近的液相段塞区，以及段塞区前面的未受扰动的多相流区域，该模型可以模拟清管及清管后整条管线流体的流动。史培玉等［2］在此基础上将管线分为4段，建立了清管器特征参数和压力计算的瞬态模型，并用数值计算方法进行求解，得到了清管过程中压力的变化规律和清管器的运动特征参数。Lima等［3］以清管器为界，将管线分为两个部分，提出了以双流体模型为基础的清管模型，并采用数值方法对模型进行求解，用来分析清管过程中流体的瞬态运动，得到了管内的压力变化规律。Esmaeilzadeh等［4］提出了气液混输管线中清管器运动的瞬态数值模型，模型将清管器的线性动量方程与液体动方程进行耦合，采用规则的四边形网格将非线性方程用非稳态的特征线法进行求解，得到了清管器位置、最优的气体流量和清管器到达管线末端的时间。

由于野战输油管线的口径较小，短管、接头和弯头等管件较多，在使用清管器时容易造成卡死或管线堵塞，因此野战输油管线更适合在不加装清管器的情况下排空。但是，前人的大部分研究都是针对固定管线使用清管器展开的，虽然对于野战输油管线有借鉴意义，但对于气液两相直接作用的排空过程的流体运动规律还没有深入研究和足够的认识，还不能指导野战输油管线的排空作业。本文针对野战输油管线不使用清管器的排空过程，建立了排空过程气液两相流动的瞬态模型，用于预测和计算排空过程中管内的流量、压力和持液率等管线运输参数，为排空作业提供参考依据。

1 排空过程的瞬态模型

排空过程管线流体的运动模型如图1所示，图中将排空过程分为纯液体段、气液混合段和纯气体段3个部分［5］。

下面分别建立3个部分的运动模型。

1.1气体运动模型

排空过程总压力为各段的摩阻和静压力之和，本文只针对水平管线，不考虑静压的影响。针对气体段的运动情况，提出如下假设:

1）气液两相没有质量交换；

2）等温绝热过程；

3）空压机提供的压力恒定。

对于气体，有连续性方程和动量守恒方程

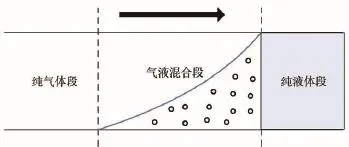
图1　野战输油管线排空示意图Fig.1 Pipeline draining model

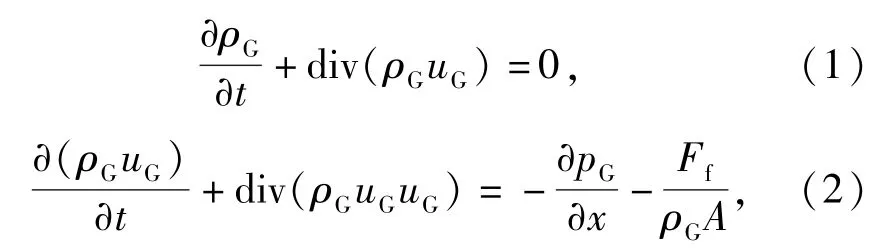
式中:ρG、uG、x、t分别是气体的密度、速度、与入口的距离和时间；pG是气体压力；A是管路的截面积；Ff是单位管长的摩阻。

1.2液体运动模型

对于纯液体部分，假设液体为不可压缩流体，其连续性方程和动量守恒方程

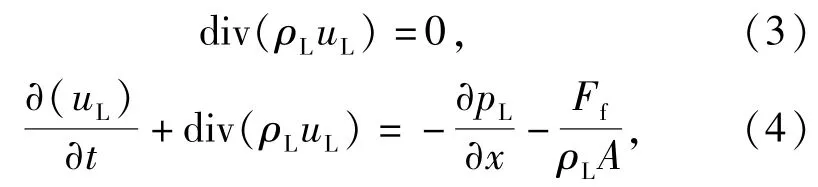
式中:ρL、uL分别是液体的密度和速度；pL是液体压力。

摩擦力Ff可由列宾宗公式求得

式中:g为重力加速度；f为摩阻系数，在紊流状态下可由文献［4］中给出的公式计算为

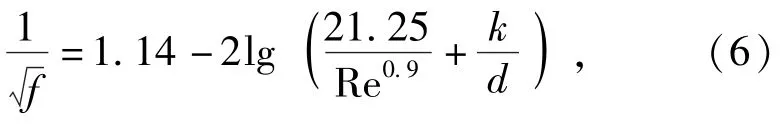
式中:d是管线直径；k是管壁粗糙度，新的无缝钢管一般取0.08［6］.

上述气液瞬态模型可以写成守恒通式形式:

1.3气液相界面耦合模型

由于气体和液体间存在气液混合段，需要分析气液间的相界面将气体运动方程和液体运动方程耦合起来。气液相界面的受力如图2所示。

在对界面进行力学平衡分析时，取dx宽度的区域，如图2所示。气体刚进入管线时，气体作用在液体表面上的力垂直于管线轴向方向，之后由于重力作用，dx宽度区域的质心不断下移，液体占据了管线的下层空间，而气体占据了管线的上层空间，气液相界面与管线轴线出现了夹角θ，随着流动的进行，这一夹角逐渐变小。那么在这一区域内，液体质心的位置可由（8）式［7］确定为

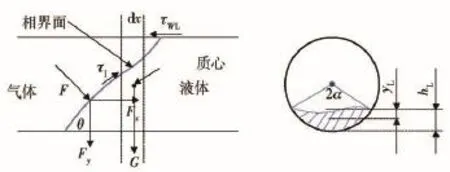
图2　气液两相界面受力分析及控制体变量Fig.2 Force analysis of gas-liquid interface and control volume variable

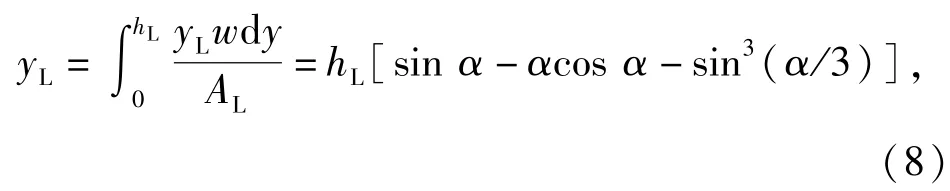
式中:w为液宽；hL为截面液位高度；yL为截面液体的质心高度；δ为液位角。在同一截面上气液两相平均压力有如下关系:

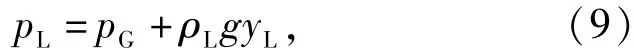
求导得

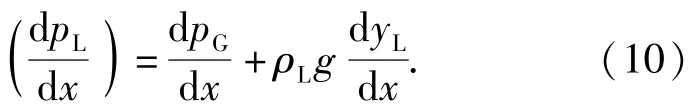
在相界面控制体内，气相的动量平衡方程为

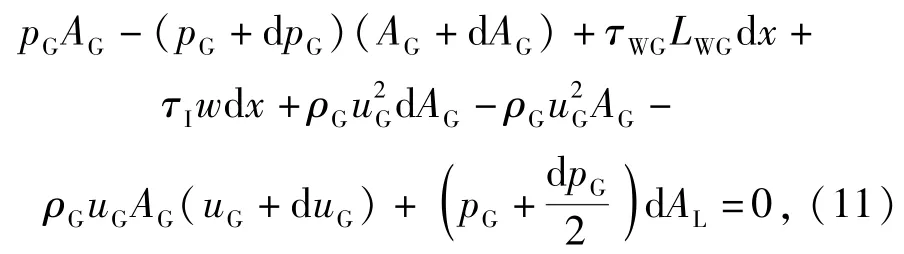
整理后得

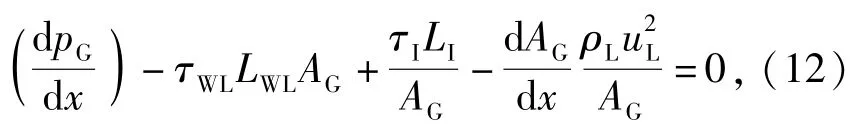
式中:τWG为管壁与气相壁面剪切应力；τ1为气液两相的剪切应力；LWG为气体与管壁的接触长度；LI为相界面长度，LI=（L-LWL-LWG）/cosθ；AG为气相占据的管线截面积。

液相的动量平衡方程为

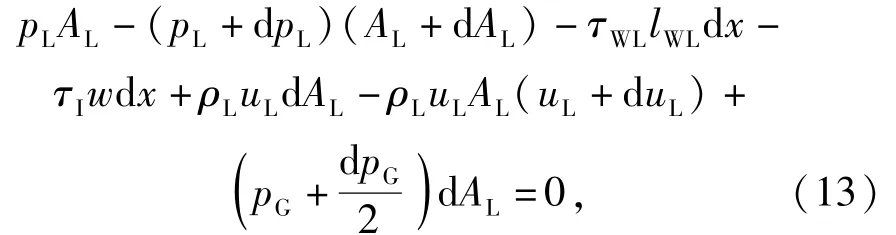
（13）式左端最后一项是考虑气液相界面倾斜的影响，整理后得

式中:τWL为液体与管壁的剪切应力；LWL为各相与管壁的接触长度；AL为气相占据的管线截面积。

考虑dAG=-dAL，由方程（10）式、（12）式、（14）式消去压力项可得

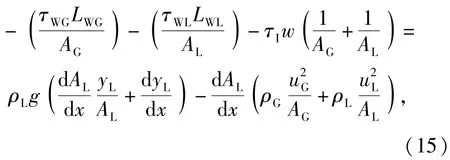
（15）式等号右边第一项可简化为

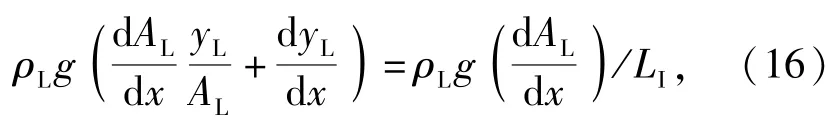
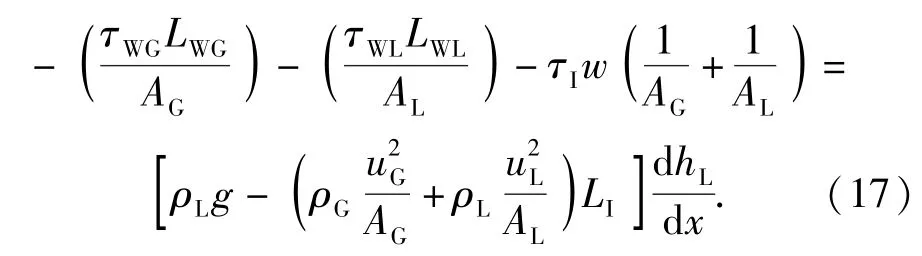
当管内出现分层流且两相界面长度达到一定程度时，由于气体与液体的表面速度差，界面可能出现失稳的情况，导致管内流型发生变化。根据K-H的界面不稳定性理论，当气液两相相对速度满足以下条件时，界面失稳，流型发生转变［9］:

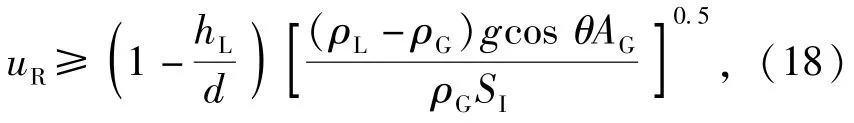
也就是当气液两相的相对速度uR达到一定值时，管内液面发生起塞现象，将（18）式变形得

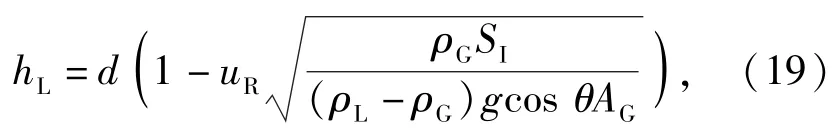
式中:uR=|uL-uG|；SI是相界面的湿周。

在管线入口的气体流量和压力（空压机的压力和流量）已知的情况下，可以通过模型得到管路上任一截面上的持液率、压力和气液速度。

1.4方程的求解

1.4.1离散方法

有限体积法具有占用内存小、收敛快、精度高的特点，在多相流及数值传热的计算中得到了广泛应用，如计算流体力学（CFD）软件中的PHOENICS、FLUENT、STAR-CD都采用了有限体积法，因此，本文也将采用这种方法对方程进行离散求解。

1.4.2离散格式

采用有限体积法对方程（7）式进行差分（见图3），它的三点显示差分格式为

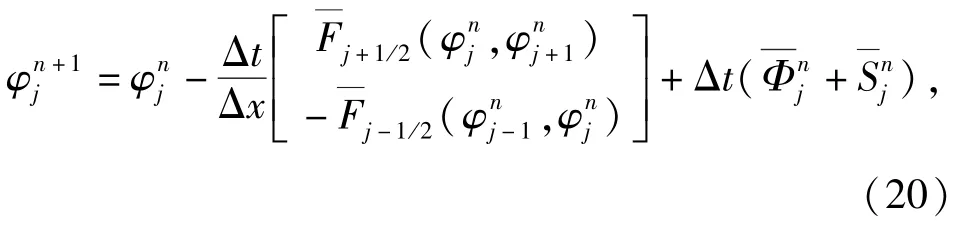
式中:Δt和Δx分别是时间和空间步长；n代表当前时步，n+1代表下一时步；j为任一控制单元代表当前时步第j单元的守恒变量代表控制单元j与j+1之间界面处得数值通量代表控制单元j与j-1之间界面处得数值通量。

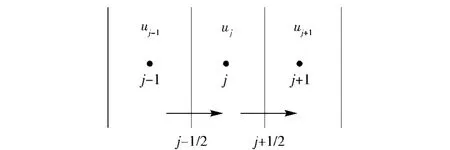
图3　三点离散示意图Fig.3 Schematic diagram of three-point discretization

1.4.3边界条件与初始条件

排空过程是具有可压流场的非稳态流动过程，操作压力选取对于模拟的鲁棒性有一定影响，将环境压力的参考位置设在管线入口，取值为1.01325× 105Pa.设置管线入口和出口均为压力边界，根据实际排空过程和前面所建管线模型特征，设置入口压力为2×104Pa，出口压力为0，以理想气体和水作为流动介质。

1.4.4网格划分

采用空间、时间的变步长，以适应外界环境变化、算法稳定性的需求，如图4所示。

本文选择稳态计算网格划分中的最小网格段，即最小微元管段Δxmin.将具有同一倾角的起伏管段，以Δxmin为单位网格进行划分，或将Δxmin进行N等分，以等分后的长度Δxmin/N取整为单位网格进行划分。其中，N取正实数，或者仅取自然数1， 2，3，…，n，以满足计算过程中不同空间步长的要求进行重新划分网格。

时间网格步长按如下方法确定:

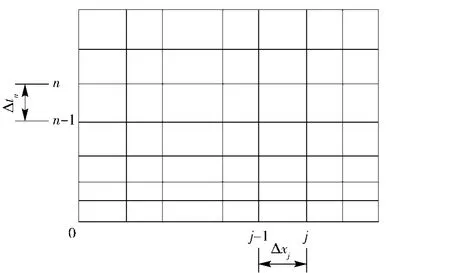
图4　空间和时间网格划分Fig.4 Space and time meshing

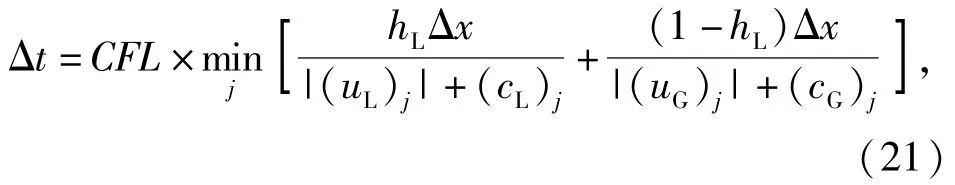
式中:CFL是库朗数，通常取0.5；c是声波在水中的传播速度。

2 实验验证

2.1实验流程

在室外铺设1100m的DN100水平管线，沿线布置6组传感器（持液率检测装置和压力变送器），每个组探针距离入口分别为126m、246m、366m、488m、780m、906m，实验流程如图5所示。实验时，用泵将储液罐中的水充满管线，这时需关闭闸阀ZF3，打开ZF1、ZF2、ZF4，充水即将结束时，先缓慢关闭ZF1再停泵，以保证水充满管线；排空时将ZF1和ZF4关闭，打开ZF2和ZF3，启动空压机，将水排回到储液罐。图5中，ZF为闸阀；Q1为气体流量计；Q2为液体流量计，P1～P6为压力变送器，T1～T6为持液率探针。

2.2沿线压力的计算

图6是空压机排气量为0.7m3/min，排气压力为0.7MPa时，沿线压力变化情况（以P1和P5为例）。

由图6可知，第1和第5个测点处压力的总体变化趋势是先升高再降低。从第1个测点来看，计算值与实测值的总体变化趋势相同，只是在排空进行到220～400s之间时，计算值略低于实测值；从第5个测点来看，计算值在300～400s之间略高实测值，其他时段计算值与实测值吻合较好。总的来讲，该模型可以较为准确地计算出整个过程压力的变化趋势。

图5　实验流程图Fig.5 Flow chart of experiment

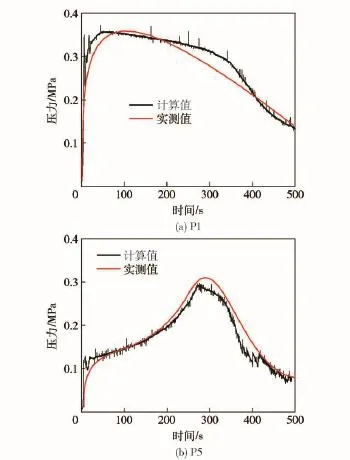
图6　排空过程压力的变化Fig.6 Pressure variation during draining

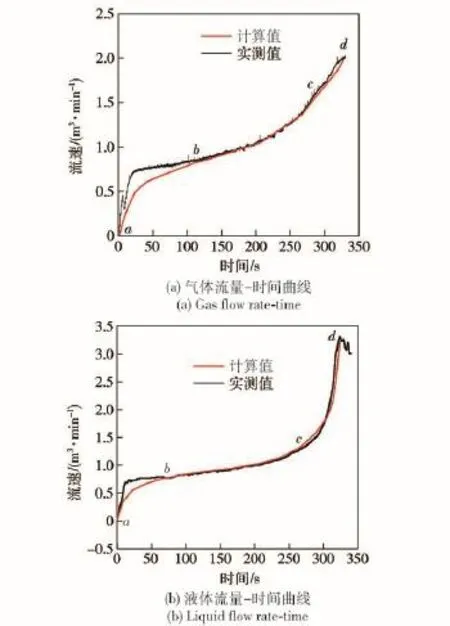
图7　气体与液体流量计算Fig.7 Calculation of gas and liquid flow rates

2.3气液流量的计算

仍然以空压机排气量为0.7m3/min，排气压力为0.5MPa的情况为例来验证气液流量的计算情况。

由图7（a）可见，排空是一个管内液体不断加速的瞬态过程，管内气体流量先是迅速增大到0.7m3/min，而后趋于平稳，当排空即将结束时大部分液体已经被排出管线，管内仅有少量液体，空压机提供的压力大于管内液体流动需要的动力，这期间气体流量又急剧增大，在此期间，计算值低于实测值，而排空进入稳定状态后，也就是b-c段和c-d段，计算值的变化趋势与实验值完全吻合。由图7（b）可见，与气体流量变化情况相似，液体流量也是不断增加，计算值与实测值在启动阶段有一定误差，但与气体流量相比，这一误差较小，而在排空后期，液体流量的计算值与实测值吻合较好。

2.4沿线持液率的计算

持液率是指气液两相流动中液体所占截面积与管线截面积的比例。图8描述的是空压机排气量为0.7m3/min，排气力为0.5MPa时的管线沿线持液率变化情况，图8（a）～图8（f）分别对应1～6号测点。

由图8（a）可知，排空进行到57s时气体到达第1个测点，管内持液率开始平滑下降，当进行到375s的时候管内持液率降到最小值0.034，说明管线底一直有较薄的液层存在，这是分层流的主要特征，这时，模型的计算值与实测值吻合较好。当排空进行到465s时，管内的持液率上升到0.76，而后又下降，这时管内有起塞现象，但持液率不为1.0，管内已经形成了准段塞流［10-11］。气体前锋到达第2个测点，如图6（b）所示，在随后的179s、219s、302s、403s时，该点的持液率急剧增加到1.0，管内已经形成液桥，虽不具有严格的周期性，但具有明显的间歇性特征，这是气液两相液塞形成的重要标志［12-13］。这时计算值与实测值的趋势基本相同，也可以反映出管内气液两相流动的间歇性和同期性，只是峰值与实测值有些差异，计算曲线比实测曲线更加平滑。当气液混合段的尾端离开测点时，持液率在0.6附近波动，表明气液混合段的末端是以波浪分层流存在的。在161s时，气体到达第3个测点，该点的持液率变化特征与第2个测点基本相似。随后，气体分别在210s、315s到达第4、5个测点。从前面的对比来看，排空大部分过程计算值与实测值吻合较好，当气体前锋到达第6测点时（361s），排空即将结束，持液率的波动非常剧烈，如图6（f）所示，说明气液混合段的末端出现环空的雾状流［14-15］，当形成雾状流时，气体为连续相，液体为分散相，当小液滴以随机方式碰撞探针时，便会出现持液率的剧烈波动，这时计算值与实测值出现一定的误差。由此可见，该模型可以较为准确地计算出排空过程的分层流、段塞流的持液率，而对于雾状流有一定的误差。

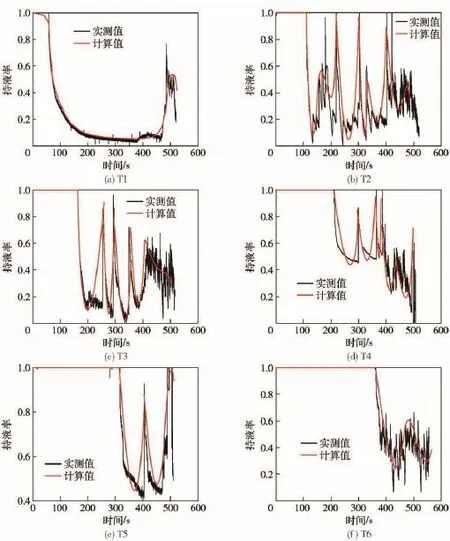
图8　排空过程各测点的持液率变化Fig.8 Variation of liquid holdup at every point during draining

3 结论

本文建立了排空过程中气体运动和液体的运动方程，对气液相界面进行了局部受力分析，推导了相界面的力学平衡方程，并将气体方程和液体方程关联起来，在空压机排气压力和排气量给定的情况下，可以计算出排空过程管内各点的压力、流量和持液率等管线运行参数。实验验证表明，该模型的准确度较高，可以用于管线排空的参数预测，为野战输油管线的排空工艺设计和作业提供参考依据。

（References）

［1］ Minami K.Transient flow and pigging in two-phase flow pipelines［D］.Tulsa:Universityof Tulsa，1991.

［2］ 史培玉，岳明，李玉星，等.水平管路清管过程流动参数变化规律模拟研究［J］.中国海上油气（工程），2003，15（6）:19-24. SHI Pei-yu，YUE Ming，LI Yu-xing，et al.A simulation study on the change of flow parameters during pigging horizontal pipeline［J］.China Off shore Oil and Gas（Engineering），2003，15（6）: 19-24.（in Chinese）

［3］ Lima P C R，Petrobras S A，Yeung H.Modeling of transient two phase flow operations and offshore pigging operations［C］∥SPE Annual Technical Conference and Exhibition.NewOrleans，US: SPE，1998.

［4］ Esmaeilzadeh F，Mowla D，Asemani M..Mathematical modeling and simulation of pigging operation in gas and liquid pipelines［J］. Journal of Petroleum Science and Engineering，2009，69（1）: 100-106.

［5］ 姜俊泽，张伟明，李正阳.管道充气排液工况下气液两相流瞬态数值模拟研究［J］.系统仿真学报2013，25（2）:383-389. JIANG Jun-ze，ZHANG Wei-ming，LI Zheng-yang.Transient mathematic simulation on gas-liquid two-phase flow of pipe pigging by gas condition［J］.Jourmal of System Simulation，2013，25（2）: 383-389.（in Chinese）

［6］ 蒲家宁.军用输油管线［M］.北京:解放军出版社，2001. PU Jia-ning.The military pipeline［M］.Beijing:PLA Publishing House，2001.（in Chinese）

［7］ 杨鲁伟，陈听宽.水平管内汽液逆流流动流型转变机理研究［J］.西安交通大学学报，1995，29（11）:5-10. YANG Lu-wei，CHEN Ting-kuan.Study on mechanism of flow pattern transition of steam-water counter current flow in horizontal tube［J］.Journal of Xi'an Jiaotong University，1995，29（11）:5-10.（in Chinese）

［8］ 姜俊泽，张伟明.水平管道气液两相段塞流参数计算的精确模型［J］.化工学报，2012，63（12）:3826-3831. JIANG Jun-ze，ZHANG Wei-ming.An accurate model for computing the parameters of gas-liquid slug flow in horizontal pipe［J］. CIESC Journal，2012，63（12）:3826-3831.（in Chinese）

［9］ 施红辉，杜凯，王超，等.不同密度梯度的多层界面上的Richtmyer-Meshkov不稳定性研究［J］.实验流体力学，2011，25（5）:45-50. SHI Hong-hui，DU Kai，WANG Chao，et al.Experimental research on Richtmyer-Meshkov instability at the multi-layered fluids interfaces with different density gradients［J］.Journal of Experiments in Fluid Mechanic，2011，25（5）:45-50.（in Chinese）

［10］ Sanchis A，Johnson G W，Jensen A.The formation of hydrodynamic slugs by the interaction of waves in gas-liquid two-phase pipe flow［J］.International Journal of Multiphase Flow，2011，37（4）:358-368.

［11］ Luo X M，He L M，Ma H W.Flow pattern and pressure fluctuation of severe slugging in pipeline-riser system［J］.Chinese Journal of Chemical Engineering，2011，19（1）:26-32.

［12］ 罗小明，何利民，吕宇玲.水平管气液两相段塞流的波动特性［J］.化工学报，2008，59（11）:2781-2786. LUO Xiao-ming，HE Li-min，LYU Yu-ling.Fluctuation characteristics of has-liquid two-phase slug flow in horizontal pipeline［J］. CIESC Journal，2008，59（11）:2781-2786.（in Chinese）

［13］ 王海琴，何利民，罗小明.水平管段塞流持液率波动规律研究［J］.工程热物理学报，2007，28（5）:795-798. WANG Hai-qin，HE Li-min，LUO Xiao-ming.Fluctuation characteristics of slug liquid holdup for slug flow in horizontal Pipe［J］. Journal of Engineering Thermophysics，2007，28（5）:795-798.（in Chinese）

［14］ 方立德，张涛，徐英，等.利用U形管测量低压环雾状流与液束环状流体积含气率［J］.化工学报，2008，29（5）: 1131-1135. FANG Li-de，ZHANG Tao，XU Ying，et al.Gas volume fraction metering with U tube in low pressure annular-mist and wispy annular two-phase flow［J］.CIESC Journal，2008，29（5）: 1131-1135.（in Chinese）

［15］ Liu S H，Sun X F，Luo J.Unified model for splash droplets and suspended mist of atomized flow［J］.Journal of Hydrodynamics，2008，20（1）:125-130.

A Transient Model of Gas-liquid Two-phase Flow for Mobile Pipeline Draining

JIANG Jun-ze，ZHANG Wei-ming，DUAN Ji-miao，YONG Qi-wei，JIANG Ming
（Department of Oil Supply Engineering，Logistics Engineering University，Chongqing 401331，China）

Draining is a routine operation of mobile pipeline.A transient model of mobile pipeline draining is established in order to improve the scientificity and efficiency of draining operation.The proposed model consists of gas kinematic equations，liquid kinematic equations and interface coupling equations. The finite volume method is adopted to solve the model，which can calculate liquid holdup，pressure and flow rate in the case of the given initial pressure and flow rate of air compressor.The accuracy of the proposed model is verified by comparing the calculated results with the experimental parameters.The result shows that the proposed model has higher calculating accuracy，and could be used to predict the parameters of pipeline operation.

petro-chemistry engineering；mobile pipeline；draining；gas-liquid two-phase flow；parameter；transient model

TE832

A

1000-1093（2016）08-1536-07

10.3969/j.issn.1000-1093.2016.08.028

2016-01-28

后勤工程学院青年基金项目（YQ13-421126）；重庆市基础科学与前沿技术研究专项资助项目（cstc2015jcyjB90001）；后勤工程学院学术创新项目（2015年）

姜俊泽（1984—），男，讲师。E-mail:154950688@qq.com