基于概率功能度量的疲劳可靠寿命分析方法

刘勤，孙志礼，钱云鹏，刘英

（1.东北大学机械工程与自动化学院，辽宁沈阳110819；2.中国兵器科学研究院，北京100089）

基于概率功能度量的疲劳可靠寿命分析方法

刘勤1，2，孙志礼1，钱云鹏2，刘英2

（1.东北大学机械工程与自动化学院，辽宁沈阳110819；2.中国兵器科学研究院，北京100089）

在分析疲劳寿命工程常用预计方法的基础上，引入功能度量法，建立疲劳可靠寿命模型，提出可靠寿命计算、灵敏度分析方法。该方法将可靠寿命的计算问题转换为一个球面约束的优化问题，只需进行一次概率功能度量的求解即可获得可靠寿命；利用计算过程的中间量，导出了可靠寿命对随机变量均值、标准差以及确定量的灵敏度计算公式。通过对某型车辆扭力轴的可靠寿命分析，证明基于概率功能度量的疲劳可靠寿命预计方法具有较好的效率和精度，灵敏度结果有效地反映出各变量对疲劳可靠寿命的影响程度。

兵器科学与技术；可靠寿命；疲劳寿命；概率功能度量；灵敏度分析

0 引言

疲劳破坏是机械构件最常见的一种失效形式，受许多随机因素的影响，疲劳寿命分散性较大［1］，因此，在进行疲劳寿命预计时，往往需要同时进行可靠性计算。工程中疲劳可靠性分析主要包括两方面内容:一是分析构件在给定寿命下的可靠度或失效概率，通常利用应力-强度干涉模型、功能函数法、模拟法等［2-3］；二是预计构件给定可靠度或失效概率下的寿命［1，4］，即可靠寿命，这往往是设计师更为关注的问题。

现有的可靠寿命预计方法，一般是假定寿命服从威布尔分布、对数正态分布等，计算分布参数，利用概率分布函数确定可靠寿命［5-6］；或者是进行多次给定寿命的可靠度计算，反复迭代，直至结果逼近给定可靠度值，从而得到可靠寿命值［7］，计算量较大。功能度量法常用于评估可靠性优化设计中的概率约束，即给定概率下的功能函数值，是一种计算高效、稳定的可靠性算法［8-10］。

本文在常规疲劳寿命预计方法的基础上，考虑影响结构疲劳寿命因素的随机性，利用功能度量法的思路，通过将疲劳寿命表示为随机变量的函数，把可靠寿命的预计问题转化为给定概率下功能函数值的计算问题，也即为概率功能度量的求解，并在功能度量法的基础上提出了计算可靠寿命及灵敏度分析方法，为工程应用提供一种适用的估算方法。

1 疲劳寿命预计的工程方法

累积损伤理论是疲劳寿命预计的基础，工程上一般采用Miner线性累积损伤理论，疲劳寿命（单位为载荷谱的重复次数）表示为

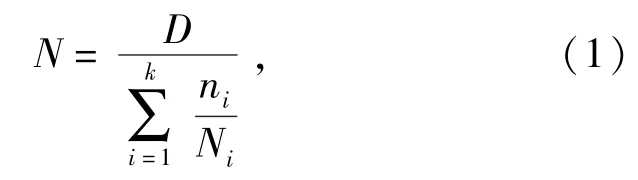
式中:D为临界损伤因子，较多场合取1；ni为第i级应力水平的循环次数（或在总循环次数中的百分比）；Ni为第i级应力水平对应的疲劳寿命；k为载荷谱的级数，当k=1时，载荷谱为恒幅谱，直接计算N1即可。各级应力水平对应的疲劳寿命预计方法，包括应力寿命法、应变寿命法、能量法和场强法、裂纹扩展寿命法等，下面将简要介绍常用的3种方法:

1）应力寿命法［11］。应力寿命法以材料或零件应力-寿命（S-N）曲线为基础，主要用于高周疲劳失效。S-N曲线在双对数坐标系中通常用两条直线和5个参数近似表示，如图1所示。NS1为第1寿命点的循环次数，一般为104，S1为对应的应力幅值极限；NS2为第2寿命点的循环次数，S2为对应的应力幅值极限，也即疲劳极限σ-1.K2为循环次数超过第2寿命点的直线斜率。以σei表示第i级应力水平的应力幅值，则Ni与σei的函数关系为

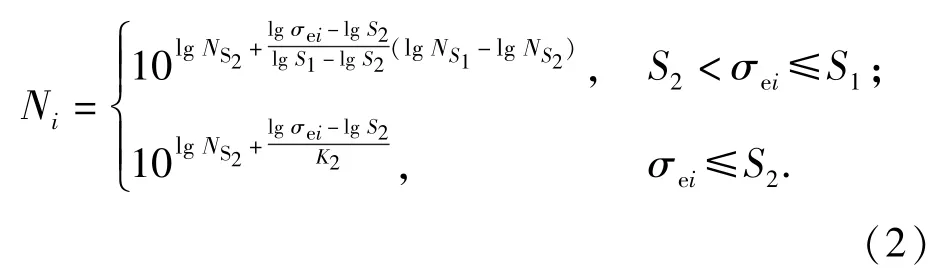
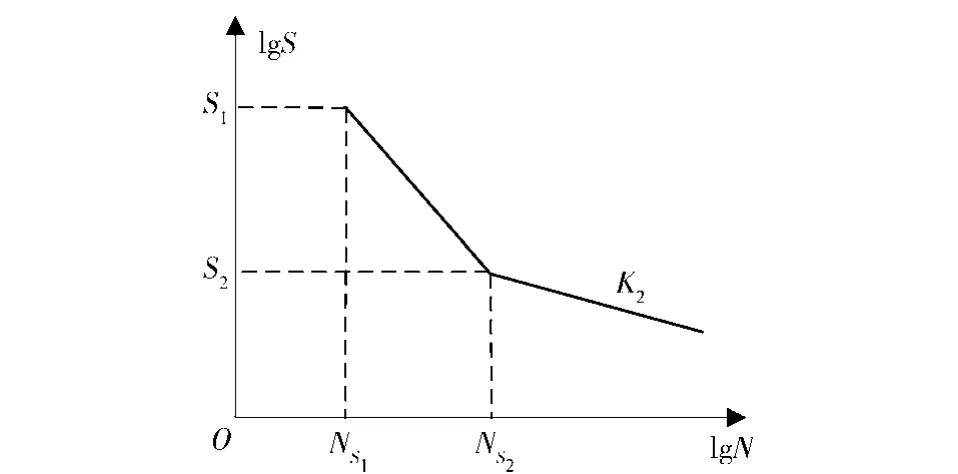
图1　材料的S-N曲线示意图Fig.1 S-N curve of material

当应力水平的均值不为0时，采用Goodman模型等进行平均应力修正，并根据构件的应力集中情况、尺寸、表面粗糙度、加工方式等，修正材料S-N曲线。

2）应变寿命法。应变寿命法是以Manson-Coffin应变-寿命关系式为基础，适应于低周疲劳失效。在计算寿命之前，通过诺伯法、有限元方法等计算结构的局部应力、应变历程，确定每个循环的应力均值σm和应变幅值εa，通过应变-寿命关系，如Morrow修正式［11］，计算寿命N:

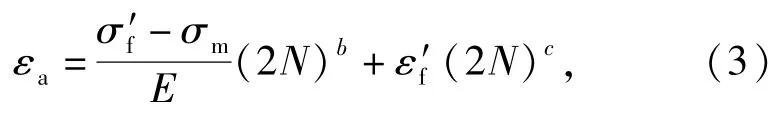
式中:σ′f为疲劳强度系数；Ε为弹性模量；ε′f为疲劳延性系数；b为疲劳强度指数；c为疲劳延性指数。由于（3）式对于N与其他参数之间的关系是一个隐式函数，无法直接写出表达式，需要先求解非线性方程，才能得到寿命值。

3）裂纹扩展寿命方法。对于含裂纹的构件，根据断裂力学理论，由Paris公式，得裂纹扩展寿命的计算式［12］为

式中:ac为临界裂纹尺寸；a0为初始裂纹尺寸；C、m为材料参数；Δσi为结构件所受的应力范围；Y为裂纹的行位和几何性质修正系数。ac的计算公式为

式中:K1c为断裂韧性。由于裂纹长度扩展是一个连续过程，对于变幅应力下的寿命估算，以循环块计的裂纹扩展寿命为

2 疲劳可靠寿命模型

根据疲劳强度理论，构件应力、应变受载荷、几何尺寸、材料力学性能的波动，是一组随机量［13］；材料的S-N曲线、应变-寿命曲线及裂纹扩展参数具有分散性，实际结构疲劳寿命亦具有较大的分散性。在实际应用中，应统计各参数的分布类型、均值和标准差，将分散性较大的参数设为随机变量x，分散性较小的参数不考虑其随机性，设为确定性变量v，归纳（1）式～（4）式4个疲劳寿命计算式，则寿命N是载荷、几何尺寸、材料性能参数等随机变量x、确定性变量v的函数，用N（x，v）统一表示，其中x为各随机变量组成的向量，v为各确定性变量组成的向量。

若已知寿命的概率分布，由概率密度函数，即可得到给定可靠度R时的寿命，即可靠寿命NR，如图2所示。

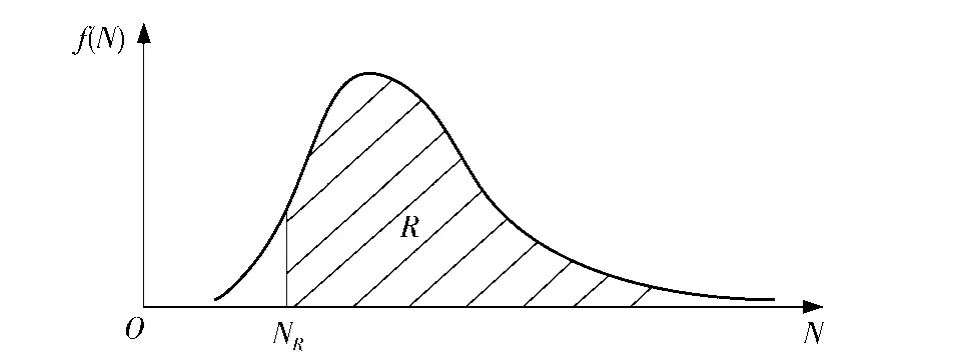
图2　可靠寿命与寿命概率密度图Fig.2 Probability density of life and reliable life

因此，构件的疲劳可靠度表示为寿命N（x，v）大于给定寿命NR的概率，即

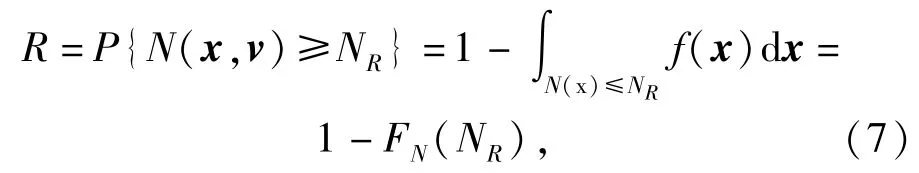
式中:f（x）为x的联合概率密度函数；FN（·）为寿命N（x，v）的累积分布函数。此外，使用矩法计算可靠度时，往往将原始随机变量向量x变换为相互独立的标准正态分布向量u，记u=T（x），在独立标准正态空间中寿命函数表示为Nu（u，v），则构件的疲劳可靠度也即为

式中:g（u）为标准正态分布向量u的联合概率密度函数。若为寿命的逆分布函数，则可靠寿命为

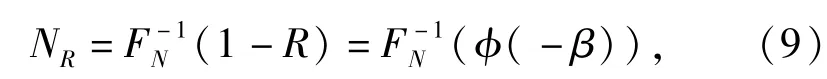
式中:β为可靠度指标，即R=φ（β）.此时，NR可称为寿命函数N（x，v）的概率功能度量，也即为待求的可靠寿命。

3 疲劳可靠寿命预计

前面给出了疲劳寿命函数，均为非线性函数，面对多个随机变量，寿命的概率密度函数、逆分布函数难以直接获得，一般需要借助近似的方法计算可靠寿命。功能度量法常用于可靠性优化设计中概率约束的评估，经过工程实践发现，相对于可靠度指标法相比，具有更高效、稳定和较少依赖于随机变量的概率分布类型等特点［14-15］。本文将借鉴该方法的思路，预计疲劳可靠寿命。

为了更好理解如何利用功能度量法求解可靠寿命，先简要介绍一次2阶矩法中可靠度系数的几何意义。在独立标准正态空间中，可靠度指标的意义是原点至极限状态曲线（或曲面）的最短距离，如图3所示。若给定寿命NR，由（7）式知Nu（u，v）= NR为极限状态曲线，则通过一次可靠度方法等能够计算该曲线离原点的距离为β=2，可靠度为φ（2）.

对于可靠寿命的求解，即为给定可靠度值φ（β），确定离原点最短距离为β的等寿命曲线（或曲面）。以两个随机变量为例，如图3所示，Nu（u，v）分别为N1、NR、N2表示一簇等寿命曲线，利用计算可靠度的方法，将会得到对应的一系列β值；反之，作半径为β=2的圆弧，寻找与该圆弧相切的等寿命曲线，切点为u*，即标准正态空间内半径为β的圆弧面上函数值最小点，则图中NR为给定可靠度φ（2）的寿命。因此，在标准正态空间中求解疲劳可靠寿命，相当于求解疲劳可靠度的逆命题。

由此，在独立标准正态空间，对于给定可靠度指标βt，疲劳可靠寿命的计算表示为如下的数学优化问题，即确定u*满足（10）式:

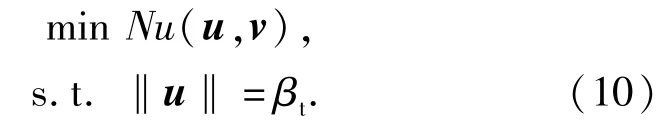
对于这一具有球面约束的优化问题，由优化问题的Karush-Kuhn-Tucker条件，最优点u*满足:

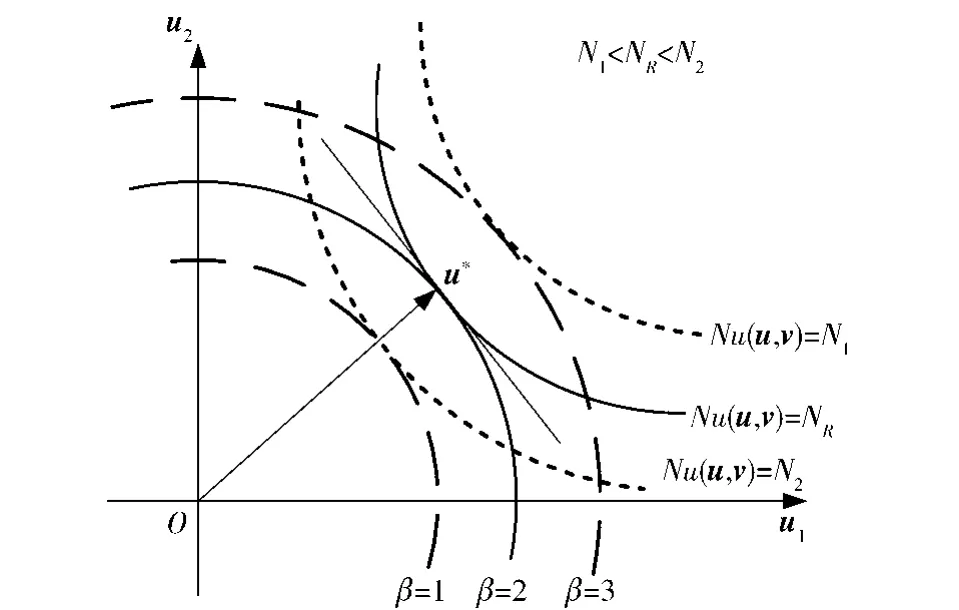
图3　标准正态空间中可靠寿命的几何意义Fig.3 Illustration of the calculation of reliable life in the standard normal space

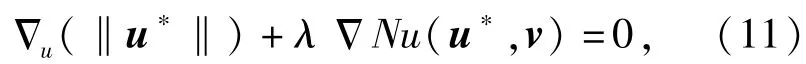
对于可靠寿命，给定可靠度一般大于0.5，故βt＞0，代入（11）式。由此得到优化计算的迭代公式为

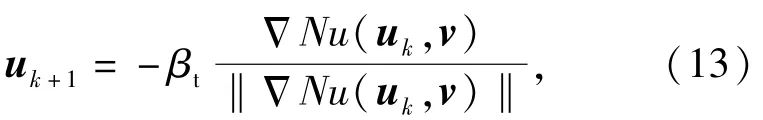
式中:梯度向量ΔNu（uk，v）为寿命函数在uk点处对各随机变量的偏导数，迭代初值可以取标准正态空间中各随机变量的均值，当‖uk+1‖-‖uk‖小于容许误差时收敛，此时求得的即为设计点u*= uk+1，将u*代入寿命函数就得到可靠寿命，即NR= Nu（u*，v）.

上述可以看出，利用本文方法求解可靠寿命，只需进行一次优化迭代计算后，就可以直接获得给定可靠度下的可靠寿命，大幅降低计算量，适合于工程应用。

4 疲劳可靠寿命灵敏度分析

4.1可靠寿命对随机变量的灵敏度分析

在计算可靠寿命的每一步迭代时需要计算的梯度向量ΔNu（u，v），在设计点u*处可靠寿命NR对随机变量xi的均值μi偏导数表示为

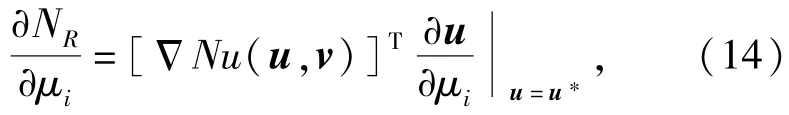
式中:

式中:y为随机变量向量转换为相关标准正态空间的向量；L为随机变量相关系数矩阵的Cholesky分解矩阵，即L与相关系数矩阵ρ的关系为ρ=L·LT；σi为随机变量xi在设计点u*的当量标准差［16-17］，其计算公式为

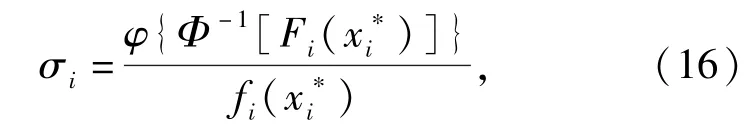
式中:Φ（·）、φ（·）分别是标准正态分布函数和密度函数，Fi（·）、fi（·）分别是随机变量xi的分布函数和密度函数。

可靠寿命对随机变量的均值灵敏度为

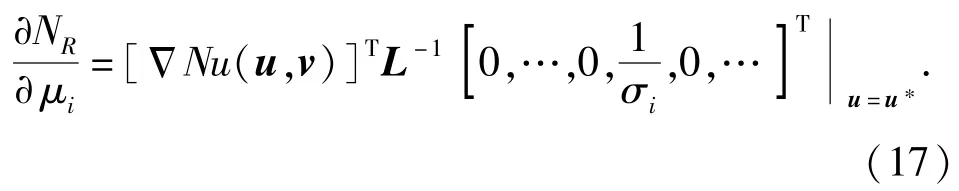
同理，可靠寿命对随机变量的标准差灵敏度为

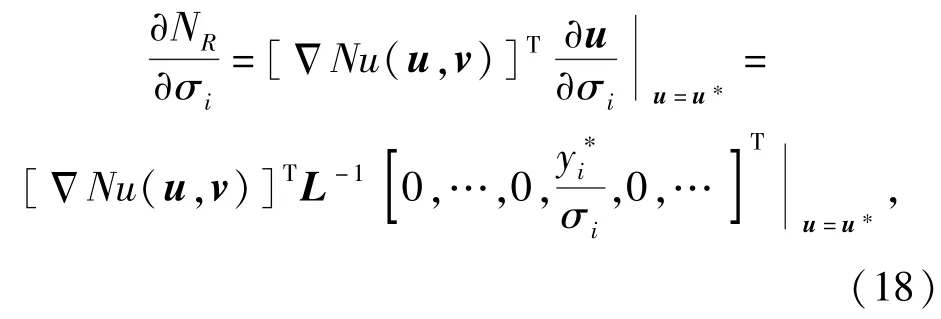
4.2可靠寿命对确定性变量的灵敏度分析

利用差分方法，在设计点u*处，设定设计变量vi赋微小的步长Δvi，则可靠寿命对确定性设计变量的灵敏度为

通过可靠寿命灵敏度分析能够得到可靠寿命对各设计变量的灵敏度，均值灵敏度和确定性量灵敏度分别反映了随机变量均值和确定性量对可靠寿命的影响。灵敏度值正负可以判断随机变量均值和确定性量对可靠寿命的影响趋势，而灵敏度值大小则反应了各设计变量对可靠寿命的影响程度，对结构设计改进时，着重考虑灵敏度值较大的变量，更容易实现结构寿命设计。

5 计算实例

某型车辆行动系统扭力轴在工程使用发生过多起断裂故障，由于加工工艺、磨损、腐蚀等原因，扭力轴表面容易存在小裂纹，通过对多根扭力轴表面裂纹测量统计，裂纹尺寸a0服从正态分布，均值为2mm，标准差0.3mm.扭力轴在工作过程中主要承受反复的扭矩作用，容易产生疲劳断裂。表1所示为扭矩幅值的块谱数据，总平均扭矩为 8280N·m，当量行驶里程为350km.试分析该扭力轴的耐久性，并提出改进措施。

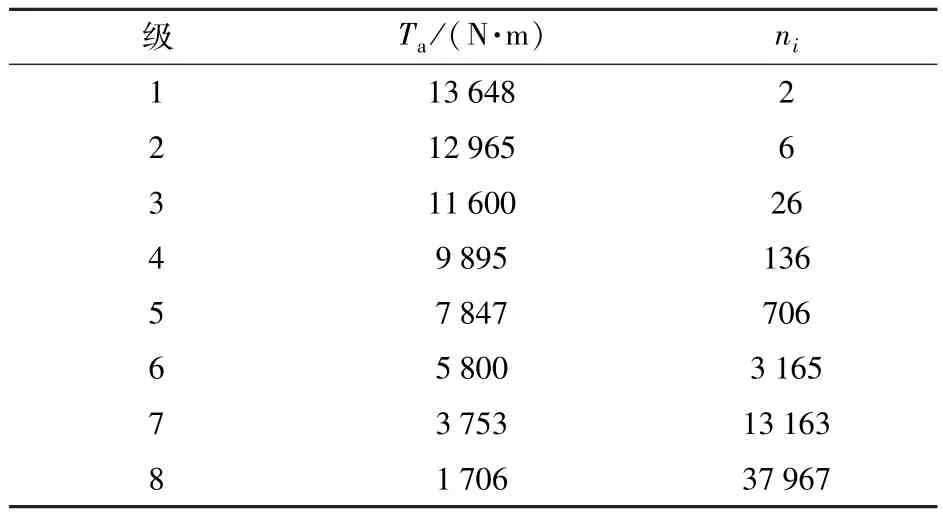
表1　扭力轴扭矩谱Tab.1 Torque spectra of a torsion shaft

对于含裂纹的构件进行寿命预计，主要采用裂纹扩展寿命法，根据（4）式，需先求解扭力轴的应力幅值。由扭力轴的扭矩幅值计算扭力轴光滑圆柱的名义切应力幅值

式中:d为扭力轴光滑圆柱部分直径，服从均值为54mm、标准差为1.6mm的正态分布。

扭力轴的应力集中部位为过渡圆弧至花键的结合处，有效应力集中系数为

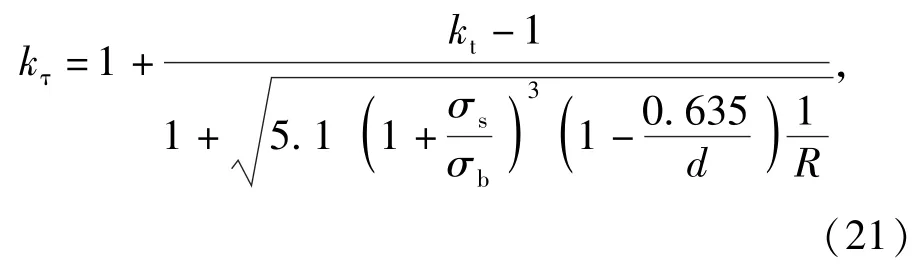
式中:R为由光滑圆柱向头部花键过渡的圆弧半径；kt为扭力轴轴颈的理论扭转应力集中系数，与R/d有关，查应力集中手册为1.05；σs、σb分别为材料的屈服强度、抗拉强度。

扭力轴材料为高强度合金钢，抗拉强度σb为1553MPa，抗拉屈服强度σs为1374MPa；断裂韧度K1c服从对数正态分布，均值、标准差分别为经试验统计，裂纹扩展参数C服从均值为2.08×10-11、标准差为0.28×10-11的正态分布，裂纹扩展参数m服从均值为2.44、标准差为0.05的正态分布，忽略C、m相关性。

利用（4）式～（6）式分别预计给定可靠度为0.5、0.9、0.95、0.99时扭力轴的寿命；同时，为对比本文方法预计结果的精度，利用蒙特卡洛模拟法（简称模拟法），即通过计算机程序按各参数随机分布生成样本组，依次计算各样本组对应的可靠寿命，为保证模拟法的计算精度，样本量设置为10万次。并且计算本文方法预计结果相对于模拟法结果的误差，一并列举于表2.

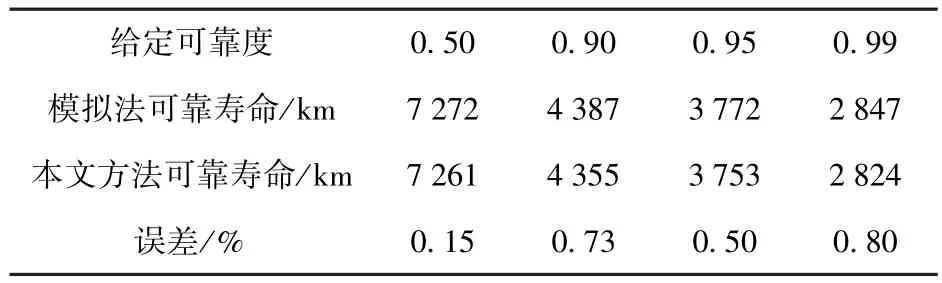
表2　可靠寿命的预计结果Tab.2 Predicted results of reliable life

从表2中结果可以看出:利用本文方法求解的可靠寿命结果，与模拟法结果非常接近；但计算量远小于模拟法的计算量，对于本例，各次求解的迭代次数均不超过5次，计算时间约为1s；而10万次蒙特卡洛模拟计算时间约480s，因此该方法的计算效率高是显著的。尤其对于调用CAE软件计算构件应力、应变，本文的方法求解可靠寿命的优势更加凸显。

针对表2中第2列结果，利用一次2阶矩法计算给定寿命为4355km的扭力轴疲劳可靠度，结果为0.897，与0.90相接近，再次验证了本文方法计算可靠寿命有较高的精度。

对于车辆，通常以B10作为可靠性指标，即可靠度为0.90的寿命，为4355km，低于工程要求，需要改进设计。利用（17）式～（19）式分析该可靠寿命对随机变量均值、标准差的灵敏度，如图4、图5分别为扭力轴可靠寿命对主要随机变量均值、标准差的灵敏度直方图。

由图4和图5可以看出，扭力轴直径d、裂纹扩展参数C和m、初始裂纹尺寸a0的均值、标准差对可靠寿命的灵敏度值较大，其影响较敏感。在扭力轴改进设计时，适当增大扭力轴直径，选取C、m较小的材料，控制初始裂纹大小，有助于提高扭力轴的可靠寿命。如将扭力轴直径均值增加2mm，同时加工上下偏差控制在±1.0mm内，经过重新计算，扭力轴的B10提高至7543km，寿命得到明显提升。

6 结论

本文将功能度量法引入疲劳寿命分析，提出了一种可靠寿命及其灵敏度分析方法。该方法将可靠寿命的计算问题转换为一个球面约束的优化问题，只需进行一次概率功能度量的求解即可获得可靠寿命，避免了可靠寿命预计之前需假设寿命服从某种分布。该方法给出了可靠寿命对随机变量均值、标准差以及确定量的灵敏度计算公式。

通过对某型车辆扭力轴的可靠寿命分析，并与蒙特卡洛模拟法、一次2阶矩法等计算结果相比较，表明基于概率功能度量的疲劳可靠寿命预计方法具有较好的效率和精度，灵敏度结果有效地反映出各随机变量对疲劳可靠寿命的影响程度。

图4　可靠寿命对随机变量均值的灵敏度比较Fig.4 Comparison of sensitivity factors for average value of each random variable

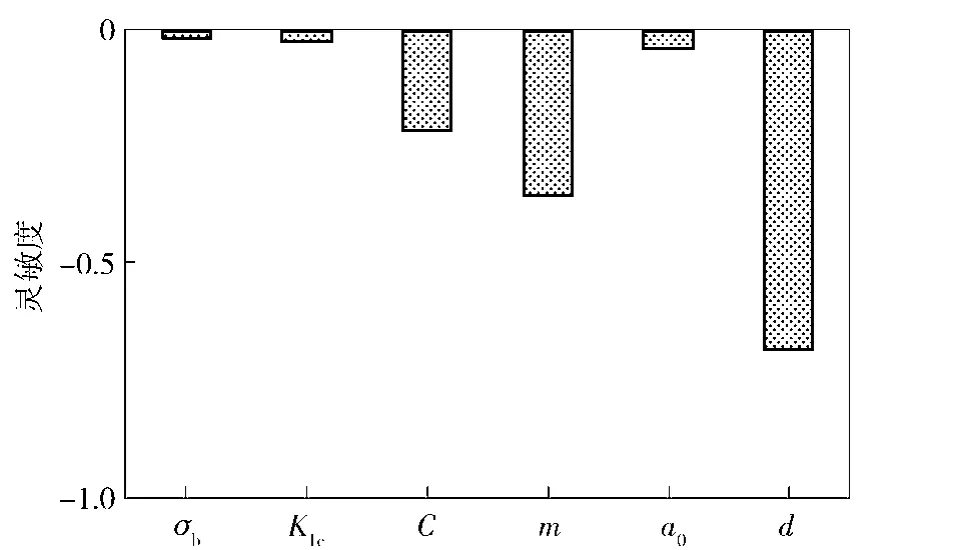
图5　可靠寿命对随机变量标准差的灵敏度比较Fig.5 Comparison of sensitivity factors for standard deviation of each random variable

（References）

［1］ 张钰，王丹，张风和，等.一种新的疲劳可靠寿命计算方法［J］.东北大学学报:自然科学版，2000，21（1）:42-45. ZHANG Yu，WANG Dan，ZHANG Feng-he，et al.New model on prediction of reliable fatigue life［J］.Journal of Northeastern University:Natural Science，2000，21（1）:42-45.（in Chinese）

［2］ Rackwitz R.Reliability analysis-a review and some perspectives［J］.Structural Safety，2001，23（4）:365-395.

［3］ Lopez I，Sarigul-Klijin N.A review of uncertainty in flight vehicle structural damage monitoring，diagnosis and control:challenges and opportunities［J］.Progress in Aerospace Sciences，2010，46（7）:247-273.

［4］ Wirsching T Y T，Martin W S.Advanced fatigue reliability analysis［J］.International Journal of Fatigue，1991，13（5）:89-394.

［5］ 谢里阳，任俊刚，吴宁祥，等.复杂结构部件概率疲劳寿命预测方法与模型［J］.航空学报，2015，36（8）:2688-2695. XIE Li-yang，REN Jun-gang，WU Ning-xiang，et al.Probabilistic fatigue life prediction method and modeling for complex strctural parts［J］.Acta Aeronautica et Astronautica Sinica，2015，36（8）:2688-2695.（in Chinese）

［6］ Zuo F J，Zhu S P，Gao H Y，et al.Stochastic fatigue life and reliability prediction based on residual strength［J］.Journal of Shanghai Jiaotong University（Science），2015，20（3）:331-337.

［7］ Guan X F，He J J，Rasselkorde E M.Probabilistic fatigue life prediction and structural reliability evaluation of turbine rotors integrating an automated ultrasonic inspection system［J］.Journal of Nondestructive Evaluation，2014，33（1）:51-61.

［8］ Tu J，Choi K K.A new study on reliability based design optimization［J］.Journal of Mechanical Design，1999，121（4）:557-564.

［9］ Ramu P，Qu X，Youn B，et al.Inverse reliability measures and reliability-based design optimization［J］.International Journal of Reliability and Safety，2006，1（1/2）:187-205.

［10］ Li G，Meng Z，Hu H.An adaptive hybrid approach for reliability-based design optimization［J］.Structural&Multidisciplinary Optimization，2015，51（5）:1051-1065.

［11］ Suresh S.Fatigue of materials［M］.Cambridge:Cambridge University Press，1998:148-233.

［12］ 杨涛，王红岩.装甲车体疲劳裂纹扩展寿命预测方法研究［J］.兵工学报，2010，31（2）:129-134. YANG Tao，WANG Hong-yan.Research on fatigue crack growth life prediction technique for the armored hull［J］.Acta Armamentarii，2010，31（2）:129-134.（in Chinese）

［13］ 徐灏.概率疲劳［M］.沈阳:东北大学出版社，1994:236-314. XU Hao.Probability fatigue［M］.Shenyang:Northeastern University Press，1994:236-314.（in Chinese）

［14］ Younes A，Alaa C.Benchmark study of numerical methods for reliability-based design optimization［J］.Structural and Multidisciplinary Optimization，2010，41（2）:277-294.

［15］ Yi P，Cheng G D，Jiang L.A sequential approximate programming strategy for performance-measure-based probabilistic structural design optimization［J］.Structural Safety，2008，30（2）: 91-109.

［16］ Rahman S，Wei D.Design sensitivity and reliability-based structural optimization by univariate decomposition［J］.Struct Multidisc Optim，2008，35（3）:245-261.

［17］ Au S.Reliability-based design sensitivity by efficient simulation［J］.Computers&Structures，2005，83（14）:1048-1061.

Reliable Fatigue Life Analysis Method Based on Probabilistic Performance Measure

LIU Qin1，2，SUN Zhi-li1，QIAN Yun-peng2，LIU Ying2
（1.School of Mechanical Engineering and Automation，Northeastern University，Shenyang 110819，Liaoning，China；2.Ordnance Science and Research Academy of China，Beijing 100089，China）

Based on the frequently-used engineering methods for fatigue life prediction and the performance measure approach，a reliable fatigue life model is built，and a set of methods for reliable life prediction and sensitivity analysis are proposed.By expressing fatigue life as the function of random variables，the reliable life prediction problem is converted into a spherical constraint optimization problem which can be solved using performance measure approach，and then the reliable life can be gotten directly.Moreover，the sensitivity factors for each random variable and deterministic variable can be calculated by using some intermediate variables in life prediction.The proposed method is demonstrated with a torsion shaft example.The results show that the proposed method has high efficiency and precision，and the different parameters have much different influences on reliable life.

ordnance science and technology；reliable life；fatigue life；probabilistic performance measure；sensitivity analysis

TB114.3

A

1000-1093（2016）08-1530-06

10.3969/j.issn.1000-1093.2016.08.027

2016-01-06

总装备部预先研究项目（51319010103）；国防技术基础项目（Z092012B001）

刘勤（1981—），男，副研究员，博士研究生。E-mail:qinlow@126.com；孙志礼（1957—），男，教授，博士生导师。E-mail:zhlsun@neu.edu.cn