论阿兰·巴迪欧哲学思想的数学基础

〔收稿时间〕2016-06-20

〔项目基金〕国家社会科学基金青年项目“阿兰·巴迪欧的‘非美学批评研究及其批评文集编译研究”（项目编号：13CWW033）。

〔作者简介〕艾士薇（1982-），女，湖北松滋人，武汉大学文学院副教授。

①Situation是巴迪欧思想中重要的关键词之一，因此，对situation的翻译十分重要。陈永国在《激进哲学：阿兰·巴丢读本》中将其翻译为“环境”，蓝江在《世纪》中将其翻译为“情势”。鉴于巴迪欧在《存在与事件》第523页的补充：“‘situation这个词汇对我们而言，具有萨特式的内涵。在这里，需要将其中立化”，并且还吸纳了盎格鲁-撒克逊学派意义上的situation。众所周知，萨特曾经创作过大量的“情境剧”，而“情境”也是

维特根斯坦学说的关键词之一，因此，笔者认为将situation翻译为“情境”更为妥当，更能体现巴迪欧思想在哲学史上的承继性与创新性。

〔摘要〕巴迪欧认为数学是本体论，是作为存在之存在的科学。他在现代分析哲学和后期海德格尔思想的基础上熔铸出属于自己的本体论。巴迪欧哲学思想的数学基础主要源于康托尔和保罗·科恩的集合理论。他结合萨特和以维特根斯坦为代表的盎格鲁-撒克逊学派的学说而提出“情境”概念，指事件发生的场所，是具有多元性的场域。他还根据集合与幂集的差异，将结构分为情境与情境状态两种类型，将集合论与哲学进行嫁接，形成独有的哲学思想 。巴迪欧认为海德格尔并没有将数学与科学区分开来，而他要做的就是实现对海德格尔反科学主义思想的超越。

〔关键词〕本体论；集合理论；情境；情境状态；结构

〔中图分类号〕B1〔文献标识码〕A〔文章编号〕1008-2689（2016）04-0104-08

在新近出版的对话录《数学颂歌》（Lloge des mathématiques）中，法国当代著名哲学家阿兰·巴迪欧毫不掩饰地表达了他对数学深沉的爱恋，以及对当下年轻人甚至哲学家们忽视数学的强烈忧虑。他在开篇又一次强调了《前提》（Conditions）一书中的观点，即真理产生的四个领域。他写道：“哲学诞生于希腊，因为在这个地方，自公元前五世纪开始，就存在着关于数学（演绎算数与几何）、艺术活动（文明雕塑、绘画、舞蹈、音乐、悲剧和戏剧）、政治（民主的发明）和激情身份（爱的传达、抒情诗……）的全新命题。因此，我认为只有当新事物真正出现在‘诸多真理（我对其进行了哲学化命名）集合中时，哲学才会展开，这些真理属于四种不同类型：科学、艺术、政治和爱。”（1）（10）也就是说，在广义的知识领域划分上，科学（数学）、艺术、政治和爱才是真理归属，也只有这四个领域中出现了全新的事件，这是哲学得以展开的前提。不仅如此，巴迪欧认为哲学家们对数学的重视和理解还远远不够，他认为理性哲学和数学实际上是诞生于同一时间，不仅不可彼此取代，而且数学还是哲学展开的前提，是事件可能出现的场所，是真理踪迹显现的场域。对巴迪欧而言，他的哲学思想与数学，尤其是与现代数学中的集合论密不可分。可以说，集合论充当着其思想的理论基石，提供了一种全新的认识世界、分析世界的方法。因此，要想系统地理解巴迪欧的哲学思想，就必须深入探究其哲学与集合论之间的逻辑关联。巴迪欧在《存在与事件》（Lêtre et Lévènement）的前言中写道：“数学是本体论——作为存在之存在的科学——这是一道光，将在思辨的场景下熠熠生辉。”（2）（10）既然数学是本体论，由此我们也就不难理解，为什么在巴迪欧的一系列著作如《主体理论》（ Théorie du sujet）、《存在与事件》以及《世界的逻辑》（Logiques des mondes）中会频繁出现如此庞杂的数学概念和公式。究其根源，巴迪欧的哲学在很大程度上是源于康托尔（Cantor）和保罗·科恩（Paul Cohen）的集合理论，而他对存在的理解，也是来自于现代数学中的基础概念。

一、 本体论与情境

巴迪欧对本体论的讨论，主要采用“情境”①这一术语，它结合了萨特和以维特根斯坦为代表的盎格鲁-撒克逊学派的学说而构成。该术语的内涵始于对海德格尔本体论的反思，海德格尔将存在（being）与存在者（beings）按照《存在与时间》1987年版本中的翻译，将“Das Seiende”与“Das Sein”（存在）相对应，将其理解为存在着的具体东西，即“存在者”。此处，笔者沿用这一翻译，以上两个词汇所对应的英文为“beings”和“being”，下文不赘。区分开来，认为“存在的‘普遍性超乎一切种的普遍性”（3）（5）。这里的存在显得更为形而上，是关于存在的抽象概念；而存在者则更加实在，可以被理解为存在的事实和存在着的事物，是可以辨识的实体。正如海氏所言，“存在者的存在本身不‘是一种存在者”（3）（8），这就将存在者与存在分别作为现实的事物与抽象的理念清晰地区分开来了。巴迪欧就是在这个意义上对存在与存在者的区分进行了反思，他认为海德格尔所提出的存在者类似于将存在实体化，与“实体”（entity）、“实存”（existant）和“客体”（object）比较接近，容易引起误解，因此在对本体论的问题进行探讨时，巴迪欧引入了“情境”概念。他说：“我将每种表现出的多元性（multiplicité）称为情境。这种表现是有效的，情境就是发生的场域，不论其所涉及的是多元性中的哪一项。每一个情境都会允许一种计为一（comptepourun）comptepourun，在数学中是指：“计为一”，就是说将某个对象视为一，英语为countasone。从集合理论的角度说，计为一是指集合中的某一项（元素或子集）属于这个集合，就被计为一，反之，如不属于该集合，则被计为零。的运算装置，它是适合情境的。为了一种呈现出的多元性，而制定了计为一的制度，而这就是对结构最广泛的界定”（2）（32）。

据此我们首先可以看到，巴迪欧将情境称为一种表现出来的多元性。然而，表现出来的多元性与多元性本身并不相同，这就像海德格尔所谓的存在与存在者一样，只是中文译文自动地展示了两者的区别，在英文中存在为being，存在者为a being，对于海德格尔来说，being is not a being，存在不是存在者。而在法语中，所有的名词都有阴阳性，几乎不可能出现英文being这样没有冠词或定冠词的名词形式，因此他们用斜体加以区分，存在为un être， 存在者为un être。莱布尼茨曾说，“ ce qui nest pas un être nest pas un être.”（2）（31）意思是说，某个对象不是实际的存在者，那么在理念上它也就不存在。这意味着，实际上并不存在的事物无法构成一种理念上的存在。正如前文所言，巴迪欧认为海德格尔这样的区分方式，会有将存在实体化为存在者的嫌疑，毕竟海德格尔认为，存在可以通过存在者或者在存在者中表现出来、为人们所感知。如果是这样的话，存在作为一个抽象概念就不可能与存在者分开了，人们每次想到存在的时候，都会想到与之相对应的具体存在者。与海德格尔关于艺术真理的看法相似，巴迪欧也认为真理是内在于艺术的，同样他也认为，存在是内在于存在物的。但就巴迪欧的本体论观点看来，作为存在身份的存在是无法被表现的，这与人们提到存在会首先想到与之相对应的存在物的情形并不相同。为了解决这一问题，巴迪欧提出了情境的概念，情境所针对的就是表现出来的多元性，也是一种表现出来的存在。当然，这种表现出来的多元性与计为一的运算装置，也就是情境中的结构，是密不可分的。“一个结构通过计算作为元素的各式各样的多元性，决定了什么属于或者什么不属于情境。元素是情境的最小单位。因此，结构生成了情境各种元素层面上的统一体（unity）。通过统一元素的多元性，它同样生成了整个情境层面的统一体。”（4）（11）换言之，这种表现出来的多元性，便是在一系列运算机制的作用下所展示出来的样态，而情境就是表现出来的多元性。不仅如此，巴迪欧意义上的情境还应被理解为某项事件发生的场所，它是一个场域，体现了某种多元性。唯其如此，情境是先于事件而存在的，因此，“‘情境这一术语，先于对物质以及/或者关系之间的各种区分，而且包含了这两者”（4）（10）。这说明情境包含了事物存在的所有特质和相互关系。“情境还意味着适应任何事物，不介意它的形式；也就是说，不管它是不是必须的、偶然的、可能的、实际的、潜在的，抑或实质的。”（4）（10）既然事件发生在情境中，那么情境必然具备一定的包容性，因此不论事件以何种形式存在，也不管它是什么性质的，皆可纳入其中。不论情境是表现出来的多元性，还是某项事件发生的场域，都可以被视为对情境的静态界定。

值得注意的是，在情境中存在着一种运算方式，叫做“计为一”。巴迪欧对它的界定是，“太一是无，一的每种效果都是一次运算的结果，即计为一。每种情境都是由这样的计算方式所构成。”原文为“LUnnétant pas， tout effet dun est le résultatduneopération， le comptepourun. Toute situation est structure par un telcompte.”首句中提到的“一”用大写，用以指代抽象的概念“一”，因此，笔者将它翻译为“太一”，以区别第二分句中的作为实体的“一”。（2）（531）之所以说太一是无，我们不妨借用中国道家哲学的观点进行参照加以理解。《道德经·中和》中指出：“道生一，一生二，二生三，三生万物”，其中的道是指世界万物的存在身份，它是不可名状之物，它可以被言说，但却无法说清楚，此时的道是混沌。从道生一，到三生万物，道成了世界万物之本源。在这个意义上，道可以被归为世界之法则，它囊括万物，无所不包，但却又什么都没有。道家将“道”理解为无，在无中生有，在有中得万物。同样，巴迪欧的太一也是如此，它是最大的有，而其本质却是无。关于这个问题，法国青年哲学家伽尔西亚是这么理解的，“‘太一是无指的是，太一（LUn）只是一种‘运算的概念，由先决的第一物质制造而成，是一种多。”（5）（32-33）这里所谓运算的概念指代的就是计为一的运算方式，而第一物质则是指自然界中自然生成的物质，并非人为促成，伽尔西亚将巴迪欧的太一理解为计为一的运算方式，由自然物质所构成，是一种多。其实，伽尔西亚这里所理解的太一，笔者认为倒并不是巴迪欧所说的太一，而更像是其文中浓墨重彩所涉及的“一”。巴迪欧在《存在与事件》中多次谈到了一，在“沉思一”中他就直言，“没有一，只有计为一。一，是一种运算，从来就不是一种表现”（2）（32）。据此我们可以明白，一是被计算出来的结果，没有一，只有计为一的运算机制，我们所认识到的一，均是一的效应，是计为一的结果。巴迪欧又进一步指出，“‘多元（multiple）Multiple在数学中为多元，例如多元微积分为multiple variable calculus，在哲学术语中，多元论、多元化所对应的英文为pluralism，而multiple一般被翻译为多样，multiplicity则为多样性。基于巴迪欧的哲学建立在数学理论的基础上，笔者将取multiple的数学术语，翻译为多元，亦可以和文中所谈到的集合理论中的多个元素相对应。同样是指计算的合成法则，也就是说，多元是由结构行为所计算的‘若干个一。”（2）（33）可见太一是一种无穷集合，包罗万象，因为它是无穷的，没有界限，本质上也就是无；而一是不存在的，只存在一的效应，即计为一后的表现形式。在《存在与事件》出版十年后，巴迪欧曾在访谈中重新谈及情境时指出，“运算装置就是情境本身”（4）（170）。显然，这种运算方式就是指计为一，从这个角度来看，我们可以将其理解为情境的动态界定。

由此我们也就不难理解为什么巴迪欧要在《存在与事件》的附录中用一句话就说明了情境，即“每一种所表现出来的一致的多元性，因此：多元，和计为一的制度，或者结构”（2）（557）。情境其实是一个综合体，其中包含了多元、计为一的制度或结构，在这种运算方式的作用下，情境成为了表现出来的一致的多元性，而这种运算方式不在别处，正是在本体论之内，内化于情境之中，是构成情境及其促成一致的多元性的重要机制。普吕斯认为，计为一的制度或者结构才是情境更为关键的特征， “它确实是组织的体系，一种计算和构造没有一（without one）的纯粹多元的方式”（6）（36）。随即他例举出了一系列被表现出的事物，从一窝小猫到一支军队，再到一场象棋博弈等等，并认为这些都是情境。实际上我们在理解情境时，应注意到情境的两个层面，不论是表现出来的一致的多元性，还是计为一的运算装置，都是情境的一部分，只是前者为静态，后者为动态，而情境就是静态与动态的完美结合，正是由于它的出现，使我们可以换一种思维来理解本体论。

二、 情境、情境状态与结构

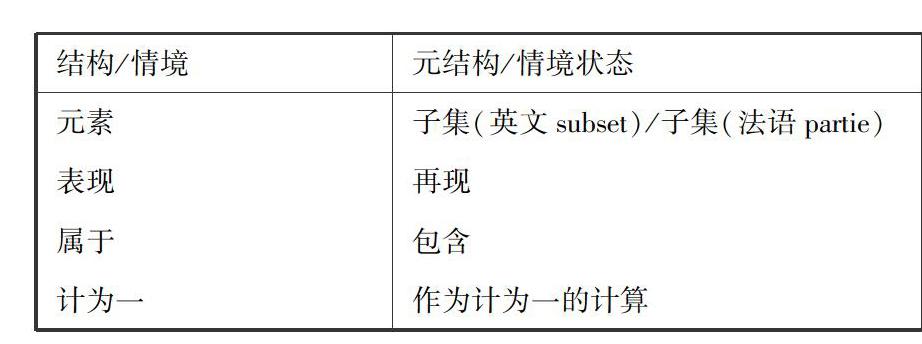
从前文中我们可以发现，巴迪欧常常使用结构这一词汇，其实这里的结构是指情境中的结构，它与情境状态相对应，体现了情境的两个层面。实际上，不论是情境还是情境状态均来自数学中的集合概念，巴迪欧创造性地将它们放到哲学的范畴中进行思考。说到这两个概念的差异，巴迪欧在1999年接受奥利弗·费尔丹的采访中就曾指出这是两个层面的问题，即表现层面与再现层面。在《存在与事件》的“表现/再现相对概念列表”（2）（119）中，巴迪欧清晰地展示了情境以及情境中的结构与情境状态之间的差异：

关于集合，从数学的角度，我们可以把情境理解为集合。就集合与其元素之间的关系而言，集合中包含了多个元素，从元素的角度认识集合，它所代表的就是多元。由此，我们也就不难理解巴迪欧为什么要把情境定义为表现出来的一致的多元。巴迪欧将这些数学概念放到哲学的范畴中，便形成了他对情境与结构的理解。数学中的“属于”，在哲学中便是“表现”，也就是说在集合理论中，元素β属于集合α，在情境中则是情境α表现其中的某一项β或者对其进行计为一的运算。巴迪欧认为，可以将属于与表现对等，将元素与情境中的项对等。由此我们可以说在情境中存在着某些多元性，它们属于情境，被情境表现出来并且进行计为一的运算，而这一切构成了情境中的结构。如果说情境中的结构主要考察的是元素，那么在情境状态中则主要考察子集。例如集合α中包含a、b、c，从这个角度看，a、b、c就是集合α的三个元素，它们属于α，因此，a、b、c就是被表现出来的多元，处于情境的结构中；同样是集合α，但是它具有8个子集，一方面元素自身可以作为集合成为α的子集，即{a}，{b}，{c}，另一方面各个元素的组合也可以构

成α的子集，如{a、b}，{a、c}，{b、c}，{a、b、c}，此外，空集{}是任何一个集合的子集，因此，这8个子集都包含在集合α中。由此可见，同样的集合，从元素与子集两个不同的角度来看，其中包含的内容大不相同，自然，得出的结论也会大相径庭。

——状态确保了情境所有约数、所有子集或者所有部分的计为一。它重新计算这一情境的各项，这些项通过这些约数被表现。

——“被包含在一个情境中”是说：通过情境状态被计算。

——因此，包含等同于通过情境的表现。我们说，它是被表现和被包含的项的一部分。

——存在一个既定集合α的所有子集合的集合。被写为P（α）P（α）被认为是集合α的幂集，也就是说，集合α中的所有子集，包括空集与α在内，所形成全部集合构成α的幂集，可以写为P（α）或2α。也就是说，α中有n个元素，那么，α中有2n个子集，因此记为2α。。P（α）的每个元素都是集合α的子集（英语的子集为a subset，法语为une partie）。

——成为子集（或者一部分）就是说：γ被α包含在内。可以写为γα。

——是包含的标志。它是导出的标志。我们可以将其定义为从属于∈。

γα

或γ∈P（α）

如果将以上8个子集当作个体构成一个集合P（α），假设γ是8个要素中的任何一个，那么，对于集合P（α）来说，γ则是它的元素，它属于集合P（α），即γ∈P（α）；集合α是P（α）中最大的子集，它与γ都是P（α）的子集之一，两者是同级关系，不论γ是哪一个子集，它都包含在集合α中，即γα。如果将这样的思维方式转入哲学领域，就会得出巴迪欧所谓的“情境状态”。在这一结构中，我们看到了计为一的计算方式，通过将各个元素组合成子集，然而此时的子集并非是被表现的状态，而是被再现。如果说在情境中的结构中，从元素到集合，包含着计为一的运算机制，那么在情境状态中，则是从元素到子集再到集合，这是计为一运算之后的又一次运算，也就是第二次计为一。在巴迪欧看来，这种运算之运算也可以被称为元结构。正如在表格下，巴迪欧所附的一段文字所言：“表现、计为一、结构、属于、元素是情境这一方面的。再现、计算之计算、元结构、包含、子集、部分是情境状态那一方面的”（2）（119）。这就清晰地说明了情境中的结构与情境状态的区别。结构属于情境层面，它“为了表现，要求计为一的制度。具有一定结构的表现（une présentation structurée）是一个情境”（2）（119）。例如有一个三口之家，其中有爸爸、妈妈和孩子，可以将它们视为这个家庭的三个元素，他们都属于这个家庭。如果我们将父母和孩子三个元素进行计为一的运算，由于“所有的情境都是通过这种运算（即计为一）被构成的”，因此，经过运算后的三个元素共同构成了它们的情境，也就是他们所属于的这个家庭集合。在这个情境中，父母、孩子都是元素，他们被视为一个整体，即被视为一家人，并且都属于这个家庭。如果我们将这样一个家庭放在情境状态中，就会有所不同。与上文中讲述的包含着a、b、c三个元素的集合α相同，这个家庭包含八个子集，对于作为集合的家庭而言，这些子集是以一种新的身份出现的，它无法像在情境中所使用的计为一的方式那样被表现，然而它却可以另一种方式被再现，将这些由家庭成员所构成的子集视为家庭集合中的元素。

通过情境与情境状态的辨析，可以说，“有两种不同的秩序或者结构支配着情境——一个认为元素首先构成了集合（其中包含了表现），另一个从不同的角度考察了这些元素，将它们当作子集，然后将它们包含于情境中或者与之相反（这里囊括了巴迪欧所说的再现。）”（6）（51）。需要注意的是，这里所说的结构并非指情境中的结构，而是跳脱出情境，包含着情境中的结构与情境状态的结构。关于这一点，巴迪欧在接受奥利弗·费尔丹的采访时做出了专门的阐释，这里的结构包含了两个层面：“首先，在表现的层面，其次，在再现的层面。我将表现和再现这两个层面的结合命名为结构。结构与情境状态并不相同，因为情境状态只是第二个层面，再现的层面。结构包含了表现的第一层面，即属于（belonging），以及第二个层面——状态，第二次计为一。我认为，结构有两种规定性，而非一种。第一个是表现层面，它只意味着，某些多元性是在情境中。第二层面，状态，包含（的层面），意味着，多元性并没有被空所篡改。结构包含了这两个层面”（4）（9）。也就是说，结构包含着情境与情境状态两个层面，而情境中又包含着结构，它以表现的形式将元素展现出来，至于情境状态则是以再现的形式使子集自我现身。之所以在这里专门提及结构与情境中结构的区别，是因为霍华德在对巴迪欧的情境范畴进行解读后总结出了以下图示（7）（99）：

这看起来与巴迪欧在接受采访时所说的内容有些不符，原因就在于他在接受采访时所说的结构与霍华德在文中提到的结构是两个不同的概念，前者包含了情境与情境状态两个部分，而霍华德所标示出的结构则是特指情境中的结构，换言之，就是后一种结构（情境中的结构）与元结构共同构成了结构。

情境的雏形已经大致展现在我们的面前，这一概念的引入是为了探讨本体论问题，正如有学者所指出的，“由于表现总是情境的——绝对不会有任何多元的任何表现是撇开情境和在情境之外的——我们能做的命名存在、思考存在（被表现的[状态]），来自情境内部”（4）（37）。这句话道出了巴迪欧引入情境来讨论本体论的真谛，即情境是思考存在的前提，存在本身是不可能脱离其固有的情境的。那么在既定的情境下，巴迪欧对本体论做出了界定。

巴迪欧一直认为“本体论=数学”。首先，他认为本体论是“作为存在的存在之科学。表现的表现。作为纯粹的多元的思想而起作用，例如康托尔的数学或者集合理论。尽管没有被划分到某个主题中（nonthématisée），在整个数学历史上，它已经是有效的了”（2）（551）。这里所说的“作为存在的存在之科学”，并不是指存在物或者存在实体，而是抽象的存在，其实在西方哲学史上，自古以来便有将数学作为世界本源的观点，在巴迪欧看来，数学的这种典范作用从柏拉图、或者有可能是从巴门尼德，一直持续到了康德。尽管，“当前哲学的‘本体论完全被海德格尔的名字所占据”（2）（15），而我们知道海德格尔素来对计数持保留态度，他所提倡的是自然和大地，提倡无蔽的状态，只是如今的科学技术似乎并没有澄明真理，也不能到达存在的彼岸。这样的观点对于当时流行的唯科学论和唯技术论来说，确实具有一定的反拨作用。然而，技术并不是数学，巴迪欧认为，此时的海德格尔似乎并没有将数学与科学区分开来，科学技术可以说是人类生产力发展以来的产物，然而，数学、数字自古希腊以来就存在了。巴迪欧在多部作品中声明，“那些可理性地被称为存在的存在……被叙述为或者毋宁说被写为纯粹的数学。并且，本体论的有效历史与数学的历史精确地吻合。”（8）（118）换句话说，在巴迪欧看来，本体论的历史其实就是数学的历史，当然，由于巴迪欧对数学研究颇深，数学拥有自己的一套独特的语言符号体系，所有的一切都可以用它加以表达。事实上，巴迪欧与古希腊时期的毕达哥拉斯以及柏拉图对数学作为本体论的观点并不完全相同，如果说毕达哥拉斯学派是用数字来理解世界的本源，那么，巴迪欧则进入了集合理论，他以集合理论为基础来理解所有的现象与状态。因此，他在对本体论的界定中特别提到了康托尔和集合理论，尽管目前人们对集合理论的认识还比较有限，但实际上，它在数学史中以及在我们对现实的理解中已经具备了相当重要的意义。

其次，巴迪欧还认为，应该“不借助一来思考纯粹的多元（multiple），本体论必须是公理性。”（2）（551）多元在巴迪欧的哲学中占据着十分重要的地位，在讨论情境与情境状态中，我们可以看到，作为元素的多元从属于集合，作为子集的多元则是包含于集合，它不需要通过与一进行对比来获得认识，它本来就具有自身存在的意义，正如有学者指出的，“在巴迪欧的词汇中，事件是一个没有根据的多元。”（9）（50）事件遵循多样性的原则，它处在常规的存在之外，它是不可预见的多元，无论是它出现的时间还是它的方式，甚至包括它是否通向真理。因此，要以多元本真的方式来理解它。正是因为“本体论=数学”，因此，本体论也像数学一样，具有公理形式，也就是说，它是不言自明的，因为本体论并不是一个情境，情境毕竟是有限的，它相当于一种适用范畴，然而本体论则并非如此，它是一个更广阔的范畴。

三、 哲学视域中的集合理论

巴迪欧将数论引入情境范畴是为了探讨哲学上的本体论问题。在他看来，本体论的历史其实就是数学的历史。巴迪欧坚信，数学拥有一套独特的语言符号体系，几乎所有的一切都可以用它加以表达。事实上，巴迪欧与古希腊时期的毕达哥拉斯以及柏拉图对数学作为本体论的观点并不完全相同，如果说毕达哥拉斯学派是用数字来理解世界的本源，那么巴迪欧则进入了集合理论，他以集合理论为基础来理解所有的现象与状态。因此他在对本体论的界定中特别提到了康托尔和集合理论，尽管目前人们对集合理论的认识相对有限，但实际上，它在数学史中以及在我们对现实的理解中已经具备了相当重要的意义。

那么，巴迪欧为什么要在本体论思考中引入集合理论呢？按照费尔丹的看法，在《存在与事件》中，巴迪欧陈述了两个原理，以支撑其对集合论的采用：“首先，关于不一致的多元性（multiplicity）学说……其次，是关于空（vide）的学说。两者共同在集合理论、集合的无穷与巴迪欧情境的多元性之间充当了桥梁。”（4）（14）我们首先要知道的是，巴迪欧所说的“不一致的多元性”指代的是什么？它是“一种纯粹的表现，正如作为‘非一的追溯性理解，因为存在-一（lêtreun）只是一种运算的结果” （2）（550）。在不一致的多元性范畴中，是不存在整一的，它被认为是计为一计算装置的运算结果。由此可见，在其中所有的事物都不是一而是多元，而这种多元性就是对那些“非一”也就是多元的表达。如果存在着一种“不一致的多元性”，那么也就必然存在着“一致的多元性”，它是指“‘众多的一所构成的多元性，其自身通过结构行为而被计算”（2）（550），此时的一已经是计算后的结果，而且相对于“不一致的多元性”，它承认一的存在。“不一致的多元性”体现为非统一化的特征，它不可能是某种个体的多元，如果它承认单独个体的存在，无疑就是说它认可了一的存在，而这正是“一致的多元性”之前提。换句话说，在“不一致的多元性”中，多元必须是由多元（多个元素）所构成的，而第二个多元，又是由另一些多元所构成，如此反复，不断地生成新的多元，构成“不一致的多元性”。如果说在本体论的探讨中，亚里士多德提出了实体，巴迪欧则主张以数学来应对。巴迪欧始终认为“本体论就是数学”，“这一主题让巴迪欧在数学术语中改良了本体论的古典语言——存在、关系和性质——更确切的说，设计和理论的数学术语，因为它是当代数学的基础教育；任何一种数学命题都可以被集合理论的语言所改写。”（4）（10）当亚里士多德提出实体时，他是相信存在统一体的，实体就是一个统一体，它在宇宙之中，也就是处于总体性中。而巴迪欧则更多地关注多元性，他引入了集合理论的思维方式与语言形式，而集合论是“一种非同一的多元性的形式理论”，这与巴迪欧所关注的“不一致的多元性”不谋而合。

其次，便是关于空的学说。空的概念不论是对于数学还是对于巴迪欧的哲学来说，都非常重要。数学中空常被理解为零，它是一个具有特殊意义的数字，连接着正数与负数，方程式的前提条件便是分母不能为零，否则该方程便失去了意义。在集合理论中，空被当作空集，即。空集是一个非常特殊的集合，它是由没有任何元素的多元所构成的，尽管没有任何元素属于空集，但它确实是存在的。而且空集是任何一个集合的子集，也就是说它不仅存在，而且还无处不在。正是在这个意义上，巴迪欧反对莱布尼茨的观点，尽管一件事物没有与其相对应的存在物或者存在者，但这并不代表着该事物不存在。作为实体的存在，也就是存在者与作为存在的存在有着相当大的区别。在巴迪欧的哲学中，空与存在紧密相连。关于空与存在的关系，可以说，《存在与事件》“沉思一”的标题直接解答了这一疑问，即“存在：多元与空”（2）（657）。存在既是多元，然而，它又是空。这种表述方式乍看是矛盾的，其实不然。之所以说存在是空，主要是基于巴迪欧关于存在与表现的哲学理念。在巴迪欧看来，本体论不是情境，因此，他认为，“存在不能在这种多元结构中自我表达。”（2）（34）这也就是说，作为本体论的存在，即存在的存在，是不能在情境中被表现出来的。尽管存在自身确实是多元的，可是它却无法表现自己。在这个意义上，无法展现的存在，在人们眼中就是空，但是作为空的存在又确实是在的。这或多或少与空集的特性有共通之处，虽然空集中并没有元素，但它却是存在的，作为空的存在虽然无法表现出来，但它也是存在的。通过上文可以发现，巴迪欧的哲学思想基本上就是建立在集合论的基础上的，不论是情境还是情境状态，抑或作为本体论的存在，以及巴迪欧哲学中的关键词——事件，可以说都是集合论在哲学领域的延伸和泛化，因此这里还需集中探讨集合理论下文中关于集合理论中的符号以及对方程式的理解，均来自巴迪欧的《存在与事件》。。

所谓集合，就是将某些确定的、可区分的事物当作一个整体来看待，而这个整体就是集合。其中，值得注意的是，空集（）属于任何一个集合；集合中众多个体，我们可以称之为元素。例如元素X为集合A中的元素之一，我们可以将其表达为 ，即元素x属于集合A， 代表着某元素属于某一集合；集合中包含的集合，可以称其为该集合的子集，例如集合B包含在集合A中，可以写为 ，那么集合B则是集合A的子集， 表示某一集合属于另一集合。按照米歇尔·波特的观点，“不容置疑的是，集合理论的语言可以用来作为交流的一种工具。”（10）（3）事实上，在集合理论中有一套独特的语言体系，例如巴迪欧在《存在与事件》中给出了一系列的公式：

（α）[（β=α）]（γ）[（γ∈β）&（γ∈α）]

（α）（β）（γ）[[（γ∈α）&λ（γ）]→（γ∈β）]

其中，α、β、γ、π等元素皆为希腊字母，有时候也会用到λ。我们将这些字母当作多元或者集合的下标，如果感觉需要的话，可以拥有更多的变量，比如1、3等。不难看出，这些标志就是我们所谈及的，也是我们表现的这个或那个元素或集合。符号为全称量词，则为存在量词，在其后面通常跟着一个变量。例如：是指：“对于所有的α而言”；指“存在着”。逻辑连接符号中，～表示否定，→表示蕴含，ou表示分离，&表示合取，表示等价。表达关系的符号有：=（相等）和∈（属于）。它们总是与两个变量连在一起：α=β，就是说“α等于β”，而α∈β，是指“α属于β”。标点为括号（），中括号[]和大括号{}。方程式为符号的集合，服从正确的法则。这些规则可以被严格制定，但它们是直观的。问题在于这些方程式是可读的。我们以第一个方程式：为例，它是指：对于所有的α而言，如果要β等于α的话，那么就必须存在一个γ，这个γ既属于β，与此同时，它还属于α。在这样的方程式中，α与γ都是定量，只有β才是自由的变量，因此这个等式在很大程度上就表达了β的属性（2）（61-62）。

现代数学中集合理论的形态多种多样，巴迪欧哲学中主要采用了康托尔和保罗·科恩的集合理论以及策梅洛-弗伦克尔理论（ZFC）。如果说康托尔是将无穷大引入了集合理论，从而启发了巴迪欧在哲学中对无穷启用，那么科恩则是在证明康托尔所提出的连续统假设（Continuum Hypothesis）中，提出了力迫法（英文为Forcing，法文为Forage），并引入了脱殊集合（英文为generic set，法语为ensemble générique），巴迪欧将这一证明过程与真理的生产融合起来，创造性地说明了真理程序的步骤。有关这一方面的内容十分复杂，笔者另有专文论述，此处不赘。这里主要结合巴迪欧的哲学介绍ZFC，以便更准确地把握巴迪欧的思想。ZFC是集合论的重要公理系统之一，它在1908年首先由策梅洛（Zermelo）提出，后经科伦斯（Skolem）、弗伦克尔（Fraenkel）改进与补充，从而建立了一个公理系统。它是康托尔（cantor）集合论方法的形式化处理，其原始概念是集合和属于关系。这一系统主要包括九条公理：“外延公理、空集公理、并集公理、幂集公理、无穷公理、分离公理、替换公理和正则公理”（11）（640）。其中，部分公理与巴迪欧的哲学思想密切相关。所谓外延公理，就是“‘任一集合都是由它的元素决定的（外延原则）形式化”（12）（146），如果要证明两个集合是否相等，只需要考察集合中的元素是否相同即可。如果其中一个集合A包含着另一集合B中没有的元素，那么集合A则大于B。外延理论既是认识集合的基础，也是认识巴迪欧哲学中情境中的结构的关键，也就是说情境中集合的元素直接决定了情境中的结构。与情境中的结构不同，情境状态主要与幂集理论相关。幂集公理是“由策梅洛于1908年首先提出。该公理断言：对于任何集合X，存在于它的所有子集组成的集合（幂集）Y=P（X）。”（11）（634）这是理解巴迪欧的情境状态概念的关键。情境状态便是由集合的所有子集构成的。任何集合的幂集永远比原来的集合大，这就是为什么情境状态在某种意义上大于情境的原因。上文中谈到了空对巴迪欧哲学的重要性，其实从某种意义上来说，巴迪欧对空的使用取自于ZFC中的空集公理，即存在一个没有元素的集合。可以表达为：“，即存在一集合，对于任意的集合y，y都不属于 ，这就是空集合。”（4）（10）这个公式意味着，空集是唯一的，空集中不包含任何其他的集合，然而，空集却包含在任何集合中，这也就构成了巴迪欧哲学中所说的作为空的存在。当然，以上笔者主要是基于巴迪欧的哲学简略地介绍了ZFC中的公理，至于集合理论中的公理系统本身，则远比上述介绍更加的复杂和高深。

诚如巴迪欧所言，应该“不借助一来思考纯粹的多元（multiple），本体论必须是公理性。”（2）（551）多元在巴迪欧的哲学中占据着十分重要的地位，在讨论情境与情境状态时我们可以看到，作为元素的多元从属于集合，作为子集的多元则是包含于集合，它不需要通过与一进行对比来获得认识，它本来就具有自身存在的意义。正因为“本体论=数学”，所以本体论也像数学一样，具有公理形式，也就是说，它是不言自明的，因为本体论并不是一个情境，情境毕竟是有限的，它相当于一种适用范畴，而本体论则是一个更广阔的范畴。

〔参考文献〕

[1]Badiou， A. Léloge des Mathématiques[M]. Paris， Flammarion， 2005.

[2]Badiou， A. Ltre et Lvénement[M]. Paris， Seuil， 1988.

[3][德]海德格尔.存在与时间[M].陈嘉映、王庆节译. 北京：三联书店，1987.

[4]Badiou， A. Infinite Thought： Truth and the Return to Philosophy [M]. trans. and ed. by Feltham， O. and Clemens， J. London& New York： Continuum， 2004.

[5]Garcia， T. De quoi Badiou estil nom？ [J].Philosophie Magazine， 2010.

[6]Badiou， E. P. A Philosophy of the New [M]. Cambridge： Polity Press， 2010.

[7]Hallward， P. Badiou： A Subject to Truth [M]. Minneapolis： University of Minnesota Press， 2003.

[8]Badiou， A. Court Traité Dontologie Transitoire [M].Paris， Seuil， 1988.

[9]de Beistegui， M. The ontolgoical dispute： Badiou， Heidegger， and Deleuze [A]. In Riera， G.（ed.）. Alain Badiou： Philosophy and Its Conditions [C]. New York： State University of New York Press， 2005， P.50.

[10]Potter， M. Set Theory and its Philosophy [M]. Oxford： Oxford University Press， 2004.

[11]《数学辞海》（第一卷），[Z]. 山西教育出版社、东南大学出版社、中国科学技术出版社，2002.

[12]张锦文.《公理集合论导引》[M].北京：科学出版社，1991.

（责任编辑：柯平）