基于LDPC/Turbo双模译码器的自适应迭代译码算法研究

2016-09-16王秀敏洪芳菲殷海兵李正权肖丙刚

浙江大学学报（理学版） 2016年5期

关键词：译码器译码误码率

王秀敏, 洪芳菲, 殷海兵, 李正权, 肖丙刚

(中国计量大学信息工程学院，浙江杭州 310018)

基于LDPC/Turbo双模译码器的自适应迭代译码算法研究

王秀敏, 洪芳菲, 殷海兵, 李正权, 肖丙刚

(中国计量大学信息工程学院，浙江杭州 310018)

针对现有WIMAX标准中LDPC/Turbo双模译码器设计在精确计算时未充分考虑迭代次数的问题，提出了一种适用于LDPC和Turbo码的自适应迭代译码算法，可灵活应用于由FPGA技术实现的双模译码器.该算法通过跟踪中间消息计算错误概率，根据多条件判定精确计算迭代次数，从而实现译码算法与错误概率变化特征的自适应性；通过改进的预判决机制减少平均迭代次数.利用Matlab搭建WIMAX系统测试链路，对TDMP多种算法的误码性能与迭代次数的关系进行测试，实现了12个SISO处理单元并行的LDPC/Turbo双模译码器.结果表明，所设计的译码器减少了算法中冗余的迭代过程，并且完全满足该标准下最大码长的要求.

LDPC/Turbo；双模译码器；迭代次数；WIMAX标准；自适应迭代译码

Journal of Zhejiang University(Science Edition), 2016,43(5):573-579

低密度奇偶校验(LDPC,low-density parity-check)[1]码和卷积Turbo[2]码是性能接近Shannon极限的纠错码，广泛应用于现代通信系统的各个领域，在多模基带接收机中都会用到LDPC码和Turbo码译码器.关于LDPC码和Turbo码的研究主要包括：高性能、高吞吐率、低消耗的LDPC/Turbo双模甚至多模译码器[3]设计与实现；具有高性能和低编码复杂度的LDPC码和Turbo码的设计；双模及多模译码器的低复杂度交织器[4]的设计等.

目前国内外都已有实现双模译码器的报道.HUNG等[5]设计了一种基4的8个SISO(soft-input soft-output)译码器并行的LDPC/Turbo双模译码器，Turbo码吞吐率可达333 Mbps，LDPC码的吞吐率可达800 Mbps.理论上，现有研究都只针对BP和MS算法的改进，例如，文献[6]在码长为无限的理想情况下制定了相应的密度演化方程，以预测平均比特错误概率.在最优参数分析上，文献[7]提出利用一种新型的停止准则：根据节点传递的后验概率求解LDPC译码器的最大迭代次数.文献[8]基于同样的思路，提出一种有效降低LDPC码解码复杂度的混合解码方法.

文献[5-8]对译码算法进行了改进和简化,计算过程只包含简单的算术过程和逻辑运算，从而便于在FPGA平台上实现，但对具体参数，比如数据量化、迭代次数、扩展因子等分析较少.为了进一步研究LDPC码和Turbo码的构造并考虑LDPC/Turbo双模译码器的实用性和可操作性，本文在双模译码器优化基础上，进行迭代次数分析.主要工作如下：

(1)在双模译码器通用算法基础上,实现了12个SISO处理单元并行的LDPC/Turbo双模译码器.

(2)提出了一种适用于LDPC和Turbo码的自适应迭代译码算法，通过多条件判定，精确计算迭代次数，从而实现译码算法与错误概率变化特征的自适应.

(3)通过预判决机制的主导作用，减少平均迭代次数.

1　双模译码器结构的实现

目前Turbo码的译码算法主要包括MAP算法、Log-MAP[9]算法、Log-MAP简化算法以及与滑窗结合的各类算法.LDPC码的译码算法主要包括BP、MS[10]、NMS、TDMP等.本文用TDMP及Log-MAP算法作为LDPC/Turbo双模译码器的译码算法.其中LDPC码和Turbo码的译码核心计算公式都涉及相同的计算函数[11]，因此只要LDPC码的TDMP[12]算法与Turbo码的Log-MAP算法，就可以在2种不同模式的译码算法LDPC和Turbo间建立关联.图1是译码器计算单元SISO共享结构图.SISO共享结构中主要涉及分支度量计算、前后向度量计算、外信息(内信息)和后验信息计算.

图1　SISO共享结构Fig.1　The sharing structure of SISO

双模译码器主要分为2部分：由自适应迭代译码算法实现的参数配置和基于FPGA技术实现的双模译码器结构.图2中SISO0-SISO11区域便是本文实现的2种算法共用模块的中心计算处理单元.此外，本文在简化双模译码器设计的基础上，创新性地引入了自适应迭代译码算法，指导LDPC/Turbo双模译码器的实现.图2简要给出了参数配置与双模结构系统的关系.从参数配置方面考虑，自适应迭代译码算法可以分别对LDPC和Turbo码进行迭代次数的分析，甄选出最适合的码率、迭代次数及偏移因子.本文主要研究迭代次数，通过对各节点消息传递变化规律的分析，采用预判决停止机制，以提高LDPC码和Turbo码的迭代译码效率，并且通过仿真，对比不同算法的迭代次数.

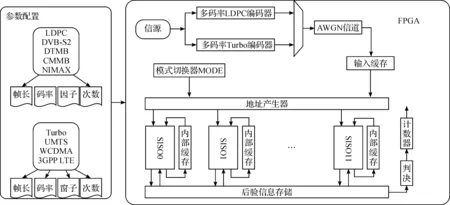
图2　双模译码器结构Fig.2　The structure of the dual-mode decoder

2　自适应迭代译码算法

在TDMP算法和Log-MAP算法中，接收到的信道消息经过解调后成为对数似然比值，并经过迭代译码运算得到更新后的对数似然比值.从LDPC校验矩阵H[13]的结构看，该校验矩阵由n个块行对应的m个超码串联而成.WIMAX标准中,LDPC码(n,k)的码长n为2 304,经过数次迭代后译出一个长为2 304的码字，而对应的Turbo码最大码长为6 144.双模译码器数据流程简图如图3所示.

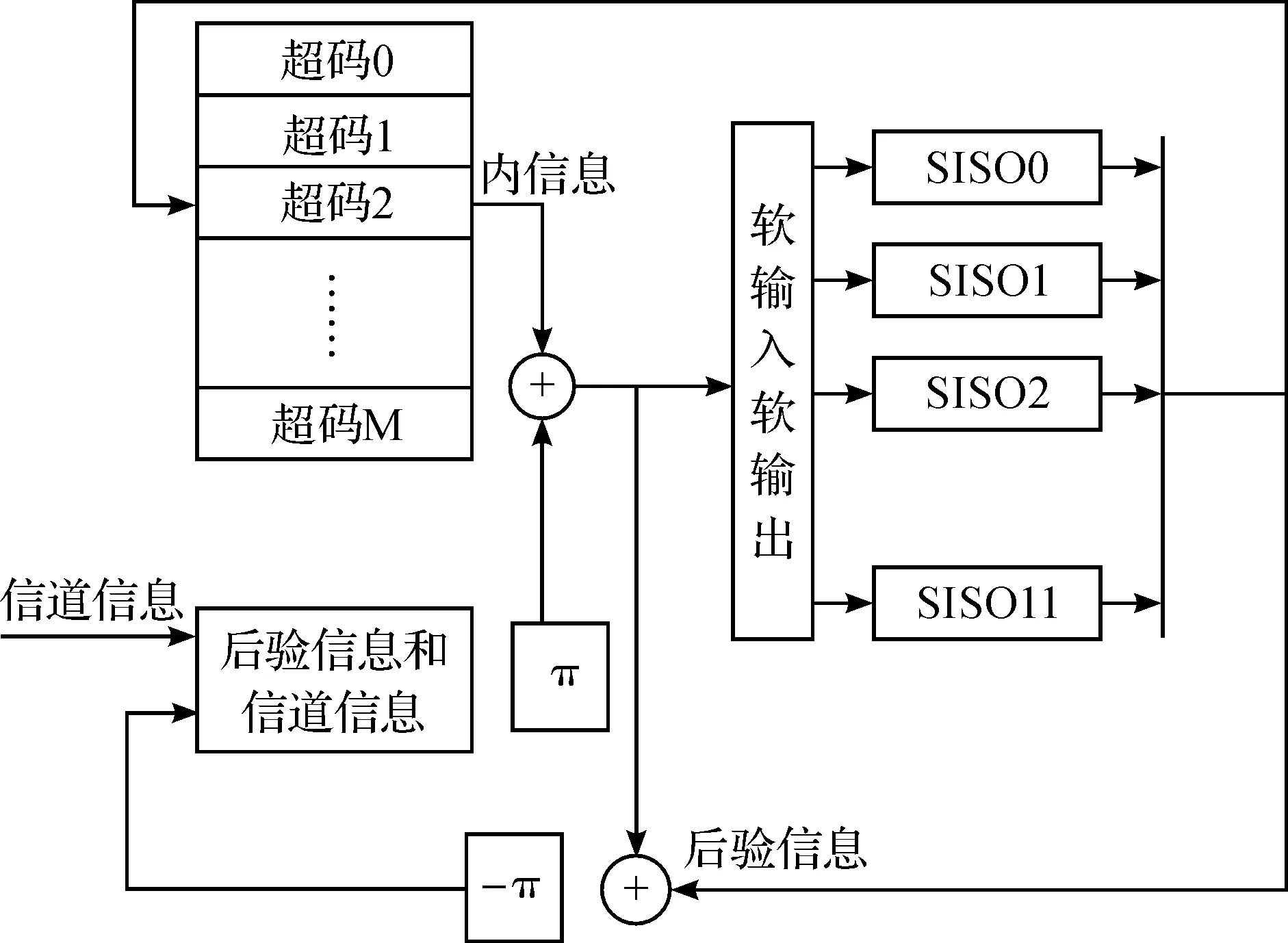
图3　LDPC和Turbo码的消息传递流程图Fig.3　The messaging flowchart of LDPC and Turbo

根据上述LDPC和Turbo码的消息传递过程，以及跟踪译码器中后验消息错误概率的变化情况，分析译码收敛特性，得到自适应迭代译码算法伪代码.

(1)初始化

iter=0,M,Pe,n，

最大迭代次数M,目标差错概率Pe，噪声功率n；

(2)开始

(3)迭代执行3种情况

迭代次数与期望误码率的关系：

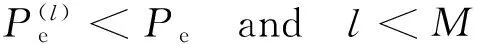
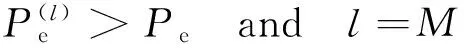
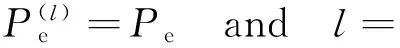
(4)结束输出

迭代过程结束,输出iter.

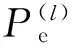
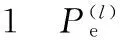
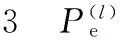
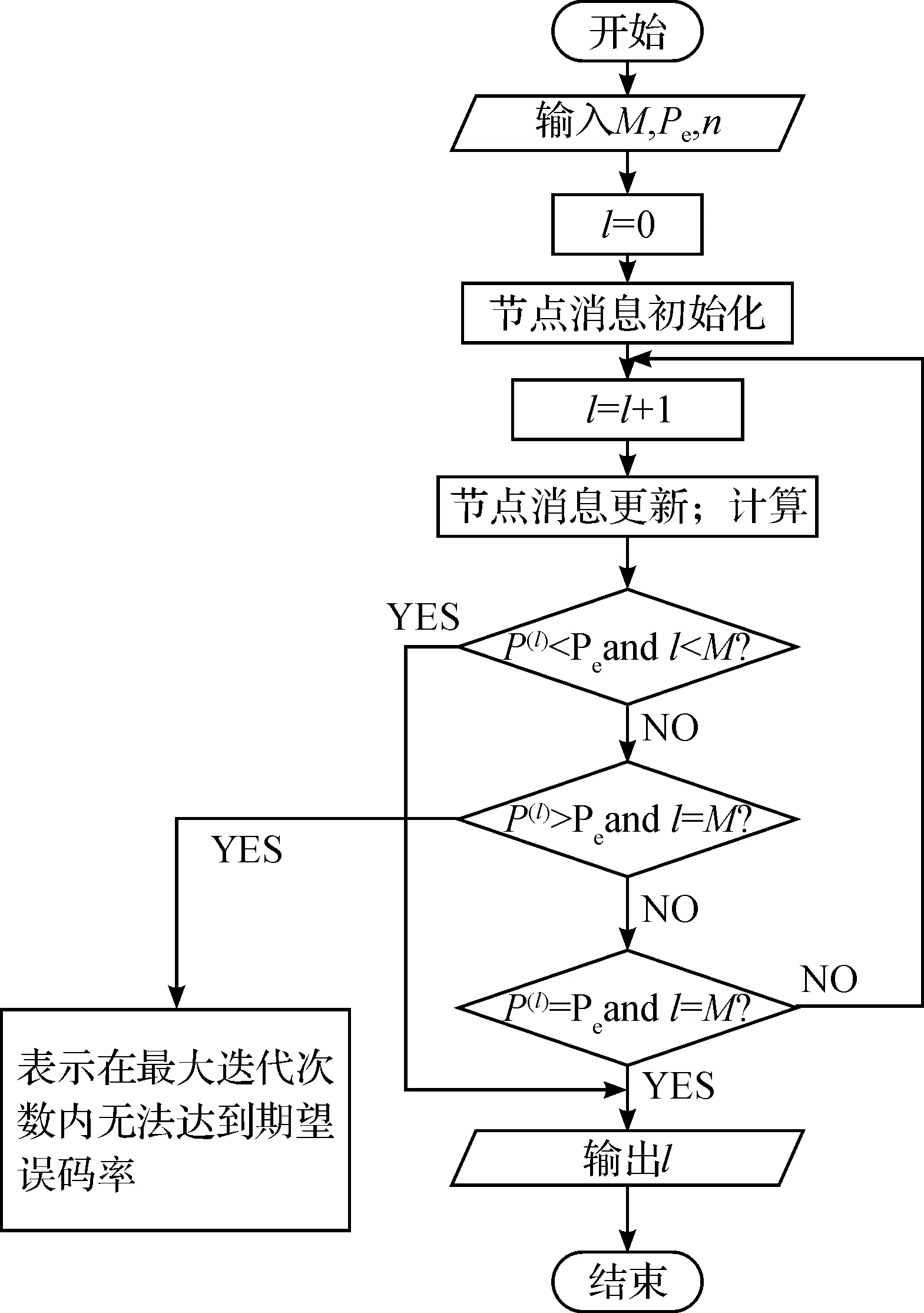
图4　迭代次数分析流程图Fig.4　The analysis flowchart of iterations

3　译码预判决机制

自提出Turbo码和LDPC码以来，众多学者对这2种码的迭代停止准则进行了分析和研究，主要可归纳为2种：基于译码器输出判决符号，即硬判决准则和基于译码器输出似然比，即软判决准则.硬判决准则的算法性能比较差，软判决准则的复杂度较高.改进后的预判决译码停止准则充分考虑了平均迭代次数、译码性能和译码计算复杂度，并进行了良好折中，而且可以在性能损失不大的情况下使译码速度得到有效提高.

目前在LDPC/Turbo双模高速译码器实现上，已有较丰硕的成果.但在FPGA平台上均采用固定最大迭代次数的方法，译码过程中迭代次数设置为一个固定值，该固定值的选取一直缺乏有力的数据支持.从LDPC码和Turbo码的译码误比特率与迭代次数的关系可以发现，误比特率随迭代次数的增加逐渐减小，但当达到一定的迭代次数后，译码的性能不再改善，此时继续迭代只会增加计算的复杂度，造成系统时延.所以在保证译码性能的前提下，应尽量减少迭代次数，以降低硬件实现的复杂度.为了解决这一问题，文献[14]提出了动态最大迭代次数可变的迭代译码方法，但其没有考虑具体的硬件实现.该方法预先将每次LDPC译码时实际使用的迭代次数与最大迭代次数的差值累加，将该累加结果作为剩余可用的迭代次数R，根据当前R值与最大迭代次数的初始值，动态调整最大迭代次数.此方法需要先将所有译码数据输入存储器，然后再进行译码，是一种非实时型译码，且需要占用大量的存储空间，在硬件资源受限的系统中不可用.

改进的预判决译码停止准则在保证译码性能的前提下，避免了类似文献[17]的冗余译码次数问题(即迭代过程中，若结果满足伴随式为零，则结束译码，否则继续迭代至所设定的最大迭代次数为止),在兼顾译码器性能和计算复杂度的情况下，适当减少了迭代次数.

4　结果分析

研究不同译码算法与迭代次数的相互关系.在Matlab仿真平台上以WIMAX标准的码率为1/2，码长为2 304的LDPC码和码长为6 144的Turbo码为例，对BP算法、MS算法、NMS算法、OMS算法、TDMP算法、TDMP-NMS算法、Log-MAP算法和Log-MAP滑窗算法的误码率和平均迭代次数进行了分析，信道模型为AWGN，采用2BPSK的调制方式.NMS算法中归一化因子α=0.9，OMS算法的β=0.125，均为该情况下的最优校正因子.用本文方法进行仿真，各译码性能曲线如图5和6所示.

图5表明，在相同噪声功率下，并且在最大迭代次数内可以达到期望误码率时，TDMP和TDMP-NMS算法的迭代次数仅为其他4种算法的1/2，这也说明TDMP和TDMP-NMS算法比其他算法的收敛速度约快一倍.从收敛速度上亦可说明，采用TDMP作为双模译码器中LDPC码的译码算法是可行的.

表1列举了各种算法在信噪比SNR为2.0，即对应的噪声n=0.631 0时的仿真数据.表2中的迭代次数是通过取大量样本点(本文采用1 000个样本点)最后求平均值得到.

仿真图图6比较了Log-MAP滑窗算法和Log-MAP算法的性能,仿真期望误码率分别为Pe=0.1，0.01，0.001和0.000 2,实验中码率R为1/2,码长为6 144.可以看到，随着PNO(噪声功率)的增大，迭代次数随之增大，但是PNO达到某一值时，误码率无法达到期望误码率pe，此时将译码次数设定为-1(如果不设为-1，那么迭代次数就是最大迭代次数M).

用本文提出的自适应迭代译码算法实现了LDPC/Turbo双模译码.上述仿真结果中当SNR为2时(设定期望误码率为0.000 5和0.000 2)，TDMP和Log-MAP算法对应的迭代次数分别为6和3.采用Cyclone IV系列的FPGA EP4CE115F29C7作为目标器件，综合结果显示，双模译码器共消耗逻辑单元个数为5.94 k，最大工作频率为68 MHz，表2为本文译码器与其他双模译码结构的吞吐率与迭代次数.从表2可以看出，本译码器在综合时钟频率较低的情况下依然获得了很高的吞吐率，同时，因为减少了迭代次数，其译码延时也较短.

图5　LDPC码不同算法的迭代次数对比Fig.5　Iterative times of LDPC codes of different algorithms

表1　不同误码率下各算法的迭代次数

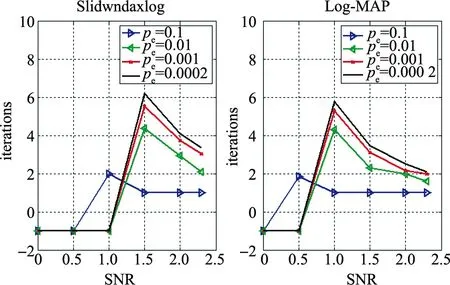
图6　Turbo码不同算法的迭代次数对比Fig.6　Iterative times of Turbo codes of different algorithms

上述结果显示，如果能在技术上优化硬件的关键路径，提高译码器的时钟频率，本译码器将非常有竞争力.

表2　双模译码器迭代次数和性能比较

5　结　论

提出了一种应用于LDPC/Turbo双模译码器的自适应迭代次数分析算法，该算法通过跟踪译码器中间消息的错误概率变化情况，分析译码收敛特性，结合改进的预判决机制，得到了特定信道下不同算法的迭代次数.在没有增加任何运算复杂度的情况下，避免了冗余的迭代过程，有效减少了平均迭代次数，适用于硬件资源受限条件下高速译码器的设计.此外，本文设计的LDPC/Turbo双模译码器可实现多码长、多通信高速译码.

[1]GALLAGER R G. Low-density parity-check codes[J]. IEEE Information Theory,1962,8(1):21-28.

[2]BERROU C, GLAVIEUX A, THITIMAJSHIMA P. Near Shannon limit error-correcting coding and decoding: Turbo-codes[C]// IEEE ICC’93. Geneva：IEEE,1993:1064-1070.

[3]SUN Y, JOSEPH R C. A flexible LDPC/Turbo decoder architecture[J]. J Sign Process Syst,2011,64(1):1-16.

[4]FONSEKA J P, DOWLING E M, BROWN T K, et al. Constrained interleaving of Turbo product codes[J]. IEEE Communications Letters,2012,16(9):58-63.

[5]HUNG L C, SHIANG Y C. Multi-mode radix-4 SISO kernel design for Turbo/LDPC decoding[J]. IEEE Very Large Scale Integration(VLSI) Systems,2015,23(10):2256-2267.

[6]ALEXIOS B S, ANDREAS B. Density evolution for Min-Sum decoding of LDPC codes under unreliable message storage[J]. IEEE Communications Letters,2014,18(5):849-852.

[7]XIA Tian, WU H C, HUANG S C H. A new stopping criterion for fast low-density parity-check decoders[C]//IEEE Global Communications Conference (GLOBECOM).Atlanta:IEEE,2013:3661-3666.

[8]WANG Hua, FAN Guangrong, KUANG Jingming. A hybrid low complexity decoding of LDPC codes[C]//Wireless, Mobile and Multimedia Networks (ICWMNN 2010), IET 3rd International.Beijing:IET，2010: 108-112.

[9]CHEN Jienan, HU Jianhao. High throughput stochastic Log-MAP Turbo-decoder based on low bits computation[J]. IEEE Signal Processing Letters,2013,20(11):1098-1101.

[10]WIBERG N, LOELIGER H A, KOTTER R. Codes and iterative decoding on general graphs[C] //IEEE Information Theory. Whistler:IEEE,1995:468.

[11]CONDO C, MARTINA M, MASERA G. VLSI implementation of a multi-mode Turbo/LDPC decoder architecture[J]. IEEE Transactions on Circuits and Systems I-Regular Papers, 2013,60(6):1441-1454.

[12]ZHAO Ming, ZHANG Xiaolin, ZHAO Ling, et al. Design of a high-throughput QC-LDPC decoder with TDMP scheduling[J]. IEEE Circuits and Systems-II: Express Briefs,2015,62(1):14-25.

[13]MARCO B, FRANCO C. Optimization of the parity-check matrix density in QC-LDPC code-based MCEliece cryptosystems[C]//Communications Workshops (ICC), 2013 IEEE International.Budapest:IEEE，2013:707-711.

[14]李刚，黑勇，周玉梅，等．动态调整最大迭代次数的奇偶校验码迭代译码方法：CN200710177791.5[P].2009-05-27.

LI Gang, HEI Yong, ZHOU Yumei, et al. Iterative Decoding Method for Dynamically Adjusting the Maximum Iteration Number of Parity Check Code:CN200710177791.5[P].2009-05-27.

[15]韩国军, 刘星成. LDPC码的信道自适应迭代译码算法[J].电路与系统学报，2010，15(1):102-107.

HAN Guojun, LIU Xingcheng. An adaptive data hiding algorithm in wavelet domain based on texture analysis[J]. Journal of Circuits and Systems,2010,15(1):102-107.

[16]LIU C H, YEN S W. CHEN C L, et al. An LDPC decoder chip based on self-routing network for IEEE 802.16e applications[J]. IEEE Journal of Solid Circuits,2008，43(3)：684-694.

[17]WANG Wenjun, WU Xiaoguang, ZHU Xiaoxuan. A 223Mbps FPGA implementation of (10 240, 5 120) irregular structured low density parity check decoder[C]//IEEE Vehicular Technology Conference.Singapore:IEEE，2008：761-771.

[18]谢天娇，袁瑞佳，陈超.基于FPGA最大迭代次数可

变的LDPC译码器设计[J].空间电子技术,2015，12(2):68-71.

XIE Tianjiao, YUAN Ruijia, CHEN Chao. A max iterative variable LDPC decoder based on FPGA[J]. Space Electronic Technology,2015,12(2):68-71.

[19]MURUGAPPA P, BAZIN J N, BAGHDADI A, et al. FPGA prototyping and performance evaluation of multi-standard Turbo/LDPC encoding and decoding[C]//Rapid System Prototyping (RSP), 2012 23rd IEEE International. Tampere:IEEE，2012:143-148.

Research on adaptive iterative decoding algorithm based on LDPC/Turbo dual-mode decoder.

WANG Xiumin, HONG Fangfei, YIN Haibing, LI Zhengquan, XIAO Binggang

(CollegeofInformationEngineering,ChinaJiliangUniversity,Hangzhou310018,China)

In view of the shortcoming that the design of LDPC/Turbo dual-mode decoder does not fully consider the precise calculation of iteration number, we propose a adaptive iterative decoding algorithm which is suitable for LDPC and Turbo codes. The algorithm is used to calculate the error probability by tracking the middle messages, and to calculate the number of iterations according to multi-conditions, thus we can achieve the self-adaptability of the variation of the decoding algorithm according to the error probability. We reduce the average number of iterations by applying an improved predecision mechanism, and build the test link of WIMAX system on Matlab platform to test the relationship between the BER performance of the multi-algorithms and iteration number, and implement the LDPC/Turbo dual-mode decoder with 12 SISOs parallel processing units. The result shows that the design of the decoder fully satisfies the requirement of the maximum code length under the standard, and can reduce the redundant iterative process.

LDPC/Turbo; dual-mode decoder; iteration number; WIMAX standard; adaptive iterative decoding