基于近似约简的集成学习算法及其在入侵检测中的应用
2016-09-05张友强杜军威刘国柱眭跃飞
江 峰,张友强,杜军威,刘国柱,眭跃飞
基于近似约简的集成学习算法及其在入侵检测中的应用
江峰1,张友强1,杜军威1,刘国柱1,眭跃飞2
(1.青岛科技大学信息科学与技术学院,青岛266061;2.中国科学院计算技术研究所,北京100190)
为了获得较大差异性的基学习器来构建集成学习器,从属性空间划分的角度来考虑集成学习问题,通过粗糙集理论定义了近似约简的概念,进一步提出了基于近似约简的集成学习算法;本方法将数据集的属性空间划分为多个子空间,基于不同子空间对应的数据集训练得到的基学习器具有较大的差异性,从而保证了集成学习器具有较强的泛化性能.为了验证本算法的有效性,本算法被应用于网络入侵检测中.在KDD CUP 99数据集上的实验表明,与传统的集成学习算法相比,本文所提出的算法具有更高的检测率和更低的计算开销,更适合于从海量高维的网络数据中检测入侵.
近似约简;集成学习;入侵检测
由于具有良好的泛化性能,近年来集成学习在机器学习和数据挖掘等领域得到了广泛关注[1].Dietterich[2]更是将集成学习列为机器学习领域的四大研究方向之首.在集成学习中,主要有2种方法来产生基学习器:基于训练样本扰动的方法和基于属性空间扰动的方法.对于前者,代表性算法包括: Bagging和Boosting[3-4].这些算法都是通过对训练样本进行重采样来产生基学习器,其中,Bagging采用等概率方式对实例重采样并训练基学习器;与Bagging方法不同,Boosting在产生后一个基学习器时,总是根据前一个基学习器的分类错误率来改变实例抽样的权重比,从而使得后一个基学习器具有较好的性能.对于后者,代表性算法主要是随机子空间法(random subspace method RSM)[5-7],该方法将训练集的属性空间随机划分成不同的属性子集,并基于多个属性子集来构建不同的基学习器.
目前的集成学习算法大多采用基于训练样本扰动的方法来产生基学习器,采用基于属性空间扰动的方法还比较少,相关研究主要集中在对RSM的一些改进和扩展[6-11].例如,Ho[6]将RSM应用于决策树学习,从而得到了决策森林算法.该算法采用RSM将数据集的属性空间随机划分为多个属性子集,然后基于每个属性子集对应的数据集来构建决策树,最后将这些决策树集成在一起来构成决策森林.在此基础上,Breiman[7]进一步将Bagging方法和RSM相结合并用于决策树学习,从而得到了随机森林算法,该算法在建立每棵决策树时,同时对数据集的实例空间和属性空间进行扰动.实验表明,随机森林算法的性能要好于决策森林.Bryll等[8]提出了一种称之为“属性Bagging”的集成学习方法,该方法首先确定一个合适的特征子集大小,然后随机选择一组固定大小的特征子集来构建集成学习器.姚旭等[9]提出了一种基于RSM和AdaBoost的自适应集成学习方法.该方法利用粒子群算法寻找使得AdaBoost依样本权重抽取的数据集分类错误率最小化的最优特征权重分布,然后根据最优特征权重分布产生随机子空间,最后用于Adaboost的训练过程中,实验结果表明该方法具有较好的性能.上述方法都是采用随机策略来扰动属性空间,从而得到不同的基学习器.然而,仅仅采用随机策略进行属性空间的划分可能是不恰当的,因为随机划分属性空间具有一定的盲目性,在很多时候,由RSM所产生的集成学习器的性能难以得到保证.对此,Guo等[11]提出了一种基于动态粗糙子空间的选择性集成学习算法DRSSE.在该算法中,使用属性的最大依赖度来减少约简的搜索空间,同时增强被选择的约简之间的差异性,DRSSE使用一个评价函数来动态平衡多个约简的学习精度和约简之间的多样性.实验结果证实了DRSSE算法比其他集成学习算法具有更好的性能.此外,胡清华等提出了一种基于粗糙子空间的集成学习算法 FS-PPEROS[12],该算法将粗糙集的属性约简技术引入到属性空间的划分中[13-14],使用多个约简来划分属性空间,从而构建不同的基学习器.为了得到足够多的约简,Hu等[12]放宽了粗糙集中属性重要性的选择标准,他们认为可以选择重要性排在第2或第3的属性作为目标属性,从而在生成约简的过程中对属性的选择进行扰动,以获得多个约简.实验表明,与RSM相比,FS-PP-EROS具有更好的泛化性能.
近年来,机器学习与数据挖掘技术在入侵检测领域的广泛应用,极大地提升了入侵检测系统的准确率,降低了其误警率.作为机器学习的一个重要研究方向,集成学习在入侵检测领域也得到了广泛应用.当前已有许多集成学习算法被应用于入侵检测系统中[15-19],例如,谭爱平等[15]提出了一种基于SVM的入侵检测集成学习算法,该算法采用SVM来训练基学习器,并利用Boosting来进行基学习器的集成.徐冲等[16]分别利用改进的BP神经网络算法和支持向量机算法来训练基学习器,并利用相应的集成学习器来检测入侵.Abdulla等[17]设计了基于粒子群优化的集成网络入侵检测系统,该集成方法使用粒子群算法产生权重来建立基学习器,使得基学习器对于入侵检测具有较高的检测率,从而使得集成学习器具有较高的检测率.Kavitha等[18]提出了基于中智逻辑分类器的集成学习入侵检测模型,由于该模型采用了中智逻辑分类器,它能够处理模糊的、不确定的、不完整的和不一致的信息,再加上使用了集成学习技术,因此该模型能够处理复杂、不确定的网络数据,实验结果证实了该模型的有效性.
集成学习能够有效提升学习系统的泛化能力,并保持较小的误差.在入侵检测中引入集成学习方法,可以在先验知识不足的情况下仍保证有较好的检测性能.然而,在面对海量、高维的网络数据时,现有的集成学习算法将面临一个挑战,即入侵检测系统的实时性难以保证,在入侵行为被系统检测出来之前,可能入侵行为就已经发生.当前的集成学习算法大多采用基于训练样本扰动的方法来产生基学习器,在处理高维数据时,这些算法将面临非常大的计算开销.因此,要想从海量、高维的网络数据中实时地检测出入侵,有必要对现有的集成学习算法进行改进[19].
针对现有的集成学习算法所存在的问题,本文提出了一种基于近似约简的集成学习算法ELAR,并利用该算法来检测入侵.ELAR算法首先利用粗糙集的属性约简技术对高维的属性空间进行降维处理,即生成多个近似约简;然后,在每个近似约简所对应的低维子空间上构建一个基学习器;最后,通过对这些基学习器进行集成,从而得到集成学习器.在低维的属性子空间上构建基学习器可以有效降低入侵检测系统的计算开销,从而保证系统的实时性.另外,本文在生成近似约简时,首先采用随机抽取的方式选择一个属性到核中,然后再通过启发式方式来选择剩余的属性,这样就可以保证不同的近似约简之间的多样性,从而使得相应的基学习器之间也具有多样性.
作为一种基于属性空间扰动的集成学习方法,ELAR与传统的RSM存在着明显的不同.RSM采用随机策略对属性空间进行划分,而ELAR则采用属性约简技术来对属性空间进行划分.虽然ELAR在确定贪心搜索的起点时也采用了随机策略,但在选择剩余的属性时都采用了贪心策略.因此,由ELAR所生成的近似约简与初始属性集具有相同或相近的分类能力,而由RSM所生成的属性子集则有可能具有非常低的分类能力,从而影响到基学习器的性能.相对于RSM,ELAR不仅可以保证基学习器的多样性,而且还可以保证每个基学习器都具有较好的性能.另外,ELAR与Hu等[12]所提出的FSPP-EROS算法也存在明显的不同.在ELAR中,本文对传统的约简定义进行了扩展,提出了近似约简的概念,并由此提出了一种近似约简算法,该算法能够产生足够多差异性大的近似约简.在FS-PPEROS中Hu等并没有对约简概念本身进行修改,而只是对属性重要性的选择标准进行了修改.另外,FS-PP-EROS中也没有引入随机策略,例如,随机选择一个属性到核中作为贪心搜索的起点,因此,该算法所生成的基学习器的多样性不一定能够得到保证.
为了验证ELAR在入侵检测中的效果,本研究利用KNN算法来训练基学习器,并在KDD Cup 99数据集上进行了实验[20].在KDD Cup 99数据集上利用ELAR来检测入侵主要包括以下4个步骤:1)在训练集上采用近似约简算法生成多个近似约简;2)在每个近似约简所对应的属性子空间上训练一个基学习器;3)将多个基学习器通过多数投票的方式集成在一起,从而得到集成学习器;4)在待检测的数据上,利用集成学习器进行入侵检测,并返回入侵检测结果.实验结果表明:与现有的集成学习算法Bagging、Adaboost和RSM相比,ELAR具有更好的性能.
1 相关概念介绍
在粗糙集中,信息表是一个四元组IS=(U,A,V,f).式中:U和A分别为对象集和属性集;V为所有属性论域的并,即,其中Va为属性a的值域;f:U×A→V为一个信息函数,使得对任意a∈A以及x∈U,f(x,a)∈Va[13-14].
进一步,A又可以划分为2个不相交的子集——条件属性集C和决策属性集D.这种特殊的信息表被称为决策表,简记DT=(U,C,D,V,f).
给定决策表DT=(U,C,D,V,f),对于任意B⊆C∪D,定义由B所决定的一个不可分辨关系IND(B)为:IND(B)={(x,y)∈U×U:∀a∈B(f(x,a)=f(y,a))}.可以证明,IND(B)是U上的一个等价关系.IND(B)将U划分成多个等价类,所有这些等价类的集合就构成U的一个划分,记为U/IND(B).
定义1[13-14](上、下近似)给定决策表DT=(U,C,D,V,f),对任意B⊆C∪D和X⊆U,X的B-上近似和B-下近似分别定义为
定义2[13-14](正区域)给定决策表DT=(U,C,D,V,f),对任意B⊆C,定义D的B-正区域POSB(D)为
定义3[13-14](核属性)给定决策表DT=(U,C,D,V,f),对任意属性 b∈C,如果POSC-{b}(D)≠POSC(D),那么称b为C中相对于D的一个核属性.所有的核属性所组成的集合CoreD(C)被称为C相对于D的核.
定义4[13-14](属性重要性)给定决策表DT=(U,C,D,V,f),对任意B⊂C和c∈C-B,属性c相对于B和D的重要性定义为
2 近似约简与基于近似约简的集成学习
在粗糙集中,一个约简就是能够分辨出对象属于不同决策值的最小属性子集.理论上来说,在一个约简后的数据集上所训练的基学习器与在初始数据集上训练的基学习器具有相同的性能.
对于一个给定的决策表,由于约简属性集和初始属性集具有相同的分类能力,因此可以在每个约简所对应的属性子空间上来训练基学习器,这样不仅可以降低基学习器的训练时间,而且还可以保证每个基学习器的性能.换句话说,可以通过粗糙集中的属性约简技术来扰动训练集的属性空间,从而构建一个集成学习器.当采用属性约简技术来扰动训练集的属性空间时,首先要解决的一个问题就是约简的数量可能不足.众所周知,不同数据集上的约简数量是不一样的.对于很多数据集而言,约简的数量非常少,最坏的情况下可能没有任何约简.当约简的数量不够时,就不能获得足够多的基学习器,从而影响到集成学习器的构建.针对上述问题,本文对传统的约简定义进行扩展,提出一种近似约简的概念,并由此提出一种近似约简算法.采用近似约简对训练集的属性空间进行扰动,可以保证约简的数量足够多,从而获得足够多的基学习器.
在传统的粗糙集约简定义中,给定一个决策表DT=(U,C,D,V,f),如果R是初始属性集C的一个约简,那么R必须与C具有完全相同的分类能力,即 |POSR(D)|=|POSC(D)|.上述关于约简的要求过于严格,从而导致很多数据集上的约简数量非常少.为了保证在每个数据集上约简的数量都足够多,有必要对上述要求进行适当的放松,即:如果R是C的一个约简,那么R与C具有相同或者相近的分类能力.通过上述修改,就得到了近似约简的概念,具体定义如下.
定义5(近似约简)给定决策表DT=(U,C,D,V,f),对任意AR⊂C,如果满足|POSC(D)|≥|POSAR(D)|≥δ×|POSC(D)|,那么称AR为C相对于D的一个近似约简,其中,δ∈(0,1]是一个给定的阈值,称δ为近似度.
从定义5可以看出,虽然近似约简AR的分类能力可能要低于初始属性集C,但是它们的分类能力是近似相等的.AR与C的分类能力的近似程度可以通过阈值δ来控制.若δ越大,则AR的分类能力就越接近于C,特别是,当 δ=1时,AR的分类能力等于C,这时AR就演变成传统的约简了.
为了获得足够多的约简来构建基学习器,本文适当放松了传统方法对约简的严格要求,虽然这种放松可能会导致AR的分类能力比C要低,从而影响到由AR所构建的基学习器的精度,但这种牺牲是值得的.因为AR的分类能力与C之间的差距可以通过阈值δ来控制,通过合理地设置δ的取值,既可以保证由AR所构建的基学习器具有较好的性能,同时又可以获得足够多的近似约简.另外,集成学习不仅仅只关注每个基学习器的性能,基学习器的多样性也是集成学习成功的一个关键因素.正如文献[21]所指出的,当基学习器达到最高的精度时,多样性必然会降低,就需要在基学习器的精度与多样性之间进行折衷,找到精度与多样性之间的平衡点.因此,适当地降低基学习器的精度,实际上是为了提升基学习器的多样性,通过获得精度与多样性之间的平衡来提高集成学习器的整体性能.
算法1给出了计算近似约简的详细步骤.
算法1计算近似约简
输入:决策表DT=(U,C,D,V,f),其中U={x1,…,xn},C={a1,…,am},近似约简的个数S,近似度δ.
输出:S个近似约简的集合Set_AR.
2)采用计数排序的方法来计算正区域POSC(D).
3)对任意a∈C,反复执行:
①采用计数排序的方法来计算正区域POSC-{a}(D);
②如果 POSC-{a}(D)≠POSC(D),则令CoreD(C)=CoreD(C)∪{a}.
4)令Rem=C-CoreD(C)表示从C中除去核之后的剩余属性集.
5)当|Set_AR|<S时,反复执行以下语句:
①令AR=CoreD(C)表示当前的近似约简.
②随机从Rem中选择一个属性r,并且令AR= AR∪{r},Rem=Rem-{r}.
③当 |POSAR(D)|<δ×|POSC(D)|时,循环执行以下操作:
(Ⅰ)对任意c∈Rem,计算属性c相对于AR和D的重要性SGF(c,AR,D);
(Ⅱ)从Rem中找出重要性最大的属性m;
(芋)令AR=AR∪{m},Rem=Rem-{m}.
④如果 AR∉Set_AR,则令 Set_AR=Set_AR∪{AR}.
6)返回S个不重复的近似约简集合Set_AR.
在算法1中,要多次计算正区域POSB(D),其中B⊆C.而为了得到POSB(D),就需要先计算出划分U/IND(B).通常,计算U/IND(B)的时间复杂度为O(|U|2|).为了降低计算U/IND(B)的时间开销,本文先采用计数排序方法对论域U进行排序,然后再计算 U/IND(B)[22],从而使得计算 U/ IND(B)的时间复杂度仅为O(|B|×|U|).
保证基学习器的多样性是集成学习的一个主要目标.为了实现这一目标,算法1将随机策略与贪心策略结合在一起来生成近似约简.在算法1的第②步中,从剩余属性集Rem中随机选择一个属性 r到当前的近似约简AR中,然后再在第③步中通过贪心策略来选择其他的属性(即每次都选择当前最重要的属性)到AR中,直到 |POSAR(D)|≥δ× |POSC(D)|.由于算法1每次贪心搜索当前近似约简的起点(即CoreD(C)∪{r})可能是不一样的(每次贪心搜索的起点都是由随机策略来决定的),因此可以有效增加不同近似约简之间的多样性,这可以保证相应的基学习器之间也具有多样性.
在算法1的基础上,本文进一步提出了基于近似约简的集成学习算法ELAR.ELAR的详细描述如算法2所示.
算法2ELAR
输入:训练集T,近似约简的个数S,近似度δ.
输出:集成学习器EL.
1)初始化:令集合E=芰.
2)在训练集T上,根据给定的近似约简个数S以及近似度δ,采用算法1计算出S个近似约简的集合Set_AR.
3)对每一个近似约简AR∈Set_AR,循环执行:
①利用AR对训练集T的属性空间进行降维,从而得到约简之后的训练集TAR;
②采用给定的学习算法在约简后的训练集TAR上进行训练,从而得到一个基学习器bAR;
③令E=E∪{bAR}.
4)通过多数投票的方式对集合E中的所有基学习器进行集成,从而得到集成学习器EL.
5)返回集成学习器EL.
3 基于近似约简的集成学习流程与实例
考虑到传统的基于RSM的集成学习所存在的不足,如基学习器分类精度低、生成的集成学习器不稳定等,本文从粗糙集的属性约简出发,定义了近似约简的概念,从而将数据集的属性空间划分为多个属性子集;然后基于每一个属性子集建立基学习器;最后通过投票的方式将这些基学习器集成起来.基于近似约简的集成学习的基本流程如图1所示.
从图1可以看出,基于近似约简的集成学习关键在于如何定义近似约简以及设计一种求解近似约简的算法,使得约简后的数据集和原始数据集具有相同或近似的分辨能力.本文采用随机策略和贪心策略相结合的方式实现了近似约简算法.上一节详细阐述了近似约简的定义、近似约简算法以及基于近似约简的集成学习算法ELAR.下面,举例说明ELAR算法的具体实现过程.
例1以UCI机器学习数据库中的trains数据集为例来说明ELAR算法的具体实现过程[23].该数据集有10个实例和32个属性,其中,决策属性集D={dec},条件属性集C={a1,a2,…,a31}.将trains数据集中的10个实例划分为2个部分,其中,前7个实例作为训练集,后3个实例作为测试集.表1给出了trains数据集的详细信息.
假设近似约简的个数S=10,近似度δ=0.9.在trains数据集上采用ELAR算法进行集成学习时,主要包括以下5个步骤:
第1步,计算核属性.首先,利用训练集来构建一个决策表DT=(U,C,D,V,f),并采用计数排序的方法计算出正区域POSC(D);然后,对于任意属性 a∈C,计算正区域 POSC-{a}(D),如果POSC(D)≠POSC-{a}(D),则将属性a作为核属性加入到集合Core中;最终,得到核属性集Core=.因此,非核属性集Rem=C-Core=C.

表1 Trains数据集Table 1 Trains data set
第2步,计算近似约简.令当前近似约简AR= Core,随机从Rem中选择一个属性(这里,属性a25被选中)加入到AR中.然后,贪心选择剩余的属性到AR中.对于任意c∈Rem,计算c相对于AR和D的重要性SGF(c,AR,D),并找出重要性最大的属性.由于当前属性a2的重要性最大,因此,将a2加入到AR中.反复执行上述过程,直到|POSAR(D)|≥0.9×|POSC(D)|.最终,得到一个近似约简AR={a2,a10,a13,a19,a25}.由于之前AR没有出现在约简集Set_AR中,因此,将AR加入到Set_AR中.
第3步,将第2步重复执行多次,直到得到全部的10个近似约简.通过多次迭代,最终Set_AR={AR1,AR2,…,AR10}={{a2,a10,a13,a19,a25},{a2,a6,a13,a19,a29},…,{a4,a10,a13,a20,a29}}.
第4步,通过每个近似约简生成一个基学习器,从而构建一个集成学习器.在训练集{x1,x2,…,x7}上,分别根据Set_AR中的10个不同的近似约简来进行训练,从而得到10个基学习器的集合E={b1,b2,…,b10}.对E中的所有基学习器进行集成,就可以得到集成学习器EL.
第5步,在测试集{x8,x9,x10}上来测试集成学习器EL的分类性能.对于测试实例x8,集合E中的10个基学习器所给出的分类结果有3个为“east”,有7个为“west”,因此,根据多数投票原则,集成学习器EL所给出的分类结果为“west”,这与x8的实际类别“west”是一致的.对于剩余的2个测试实例x9和x10,采用同样的方法进行测试,EL所给出的分类结果与它们的实际类别也是一致的.
4 实验
4.1实验环境与实验数据
下面,通过实验来验证ELAR对于入侵行为的检测能力.实验采用著名的 KDD Cup 99数据集[20],该数据集包含了约49万条连接记录,总共有24种攻击类型,这些攻击类型又进一步被分为DOS、R2L、U2R和Probe四大类[20].实验采用KNN算法来训练基学习器,并将ELAR与传统的集成学习算法Bagging[3]、Adaboost[4]以及RSM[5]进行了比较,其中Bagging和Adaboost是2个具有代表性的基于训练样本扰动的集成学习方法,而RSM则是具有代表性的基于属性空间扰动的集成学习方法.
实验的硬件环境为:Intel处理器2.0 GHz,2 GB内存.本研究采用Java语言实现了ELAR和KNN算法.对于RSM、Bagging和Adaboost这3种算法,则直接使用Weka中提供的算法进行实验[24].
由于KDD Cup 99过于庞大,并且包含了太多冗余的信息,因此,仿照陈仕涛等[25]的实验方法,从KDD Cup 99的一个10%子集“10%-KDD”中随机抽取出一定比例的数据来进行实验[20].具体的抽取策略如下:1)对于10%-KDD中样本数比较少的类别,所有样本都被抽取;2)对于10%-KDD中样本数比较多的类别,随机抽取其中10%的样本;3)对于10%-KDD中样本数最多的几个类别,只抽取其中1%的样本.根据上述抽取策略,最终得到了一个包含6 338条记录的数据集“Sample-KDD”.
表2分别给出了10%-KDD和Sample-KDD中各种攻击类型以及正常连接的记录数.
Sample-KDD数据集总共有41个条件属性,其中34个是连续型属性,只有7个是离散型属性[20].由于粗糙集更适合于处理离散型数据,因此,在计算近似约简之前,本文预先对Sample-KDD中的连续型属性进行了离散化处理,离散化算法主要采用等宽区间 (equal width binning,EW)和等频区间(equal frequency binning,EF)这 2种常用的算法[24].
4.2实验步骤与设置
1)离散化与数据准备.本文分别采用Weka中提供的EW和EF算法来离散化Sample-KDD中的连续型属性.对于EW和EF,它们的区间数都设置为3[24].
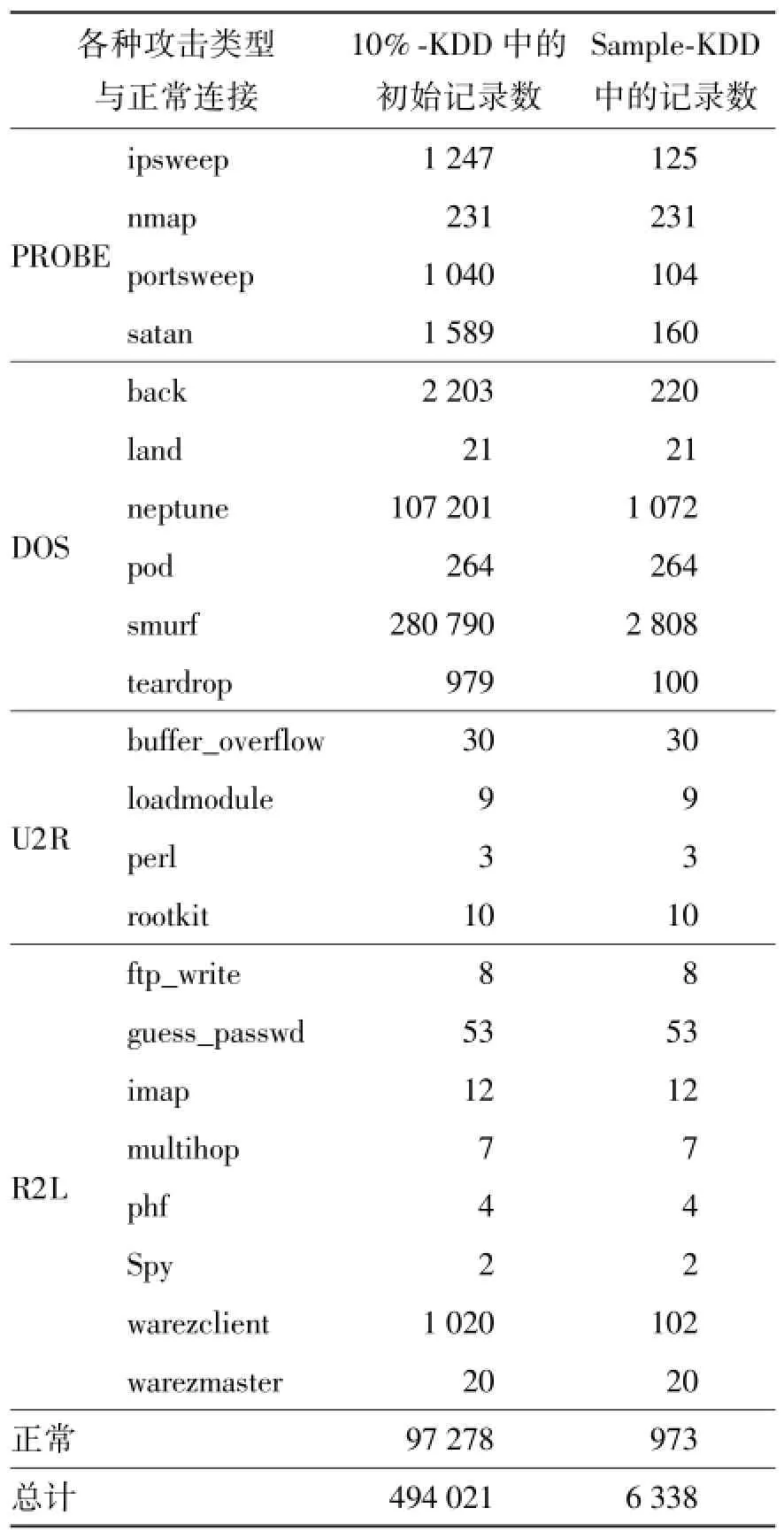
表2 各种攻击类型以及正常连接的记录数Table 2 Number of records for various attack categories and normal connections
需要指出的是,虽然Sample-KDD中包含了34个连续型属性,但是其中有8个属性的取值个数非常有限,没有必要对它们进行离散化[20].因此,本文只针对其中26个连续型属性进行了离散化.对于每个经过EW或EF离散化之后的Sample-KDD数据集,随机选择其中60%的数据作为训练集,并将剩余40%的数据作为测试集.
2)基学习器的生成.对于ELAR算法,首先在训练集上计算出S个近似约简,其中S被设定为10.然后,针对每个近似约简AR,利用AR对训练集的属性空间进行降维,并采用KNN算法在约简后的训练集上进行训练,从而得到S个基学习器.
对于RSM、Bagging和Adaboost这3种算法,直接使用Weka中所提供的算法来生成基学习器,其中RSM的子空间维数设为21(即每个随机子空间包含21个属性).这3种算法的集成规模(即基学习器的个数)均设为10,而其他参数的设置则使用Weka中的默认值.
由于KNN算法的性能依赖于参数k的取值,因此,针对k=1,3,5分别做了3组不同的实验.
3)集成学习器的生成与入侵检测.将前面所生成的10个基学习器集成在一起,从而得到一个集成学习器.最后,在测试集上利用该集成学习器来检测入侵.
对于ELAR算法,本文采用多数投票的方式将所有的基学习器集成在一起,并由此来检测入侵.对于RSM、Bagging和Adaboost这3种算法,仍然使用Weka中所提供的算法来构建集成学习器以及在测试数据上来检测入侵,相关参数的设置均采用Weka中的默认值.
为了更准确地评估每个算法的入侵检测性能,本文将每个算法都重复执行10次,并取这10次检测结果的平均值作为最终的入侵检测结果.
4.3实验结果
表3~5分别列出了当k取1、3和5时各个集成学习算法在Sample-KDD上的入侵检测结果,其中,EW算法被用来对Sample-KDD进行离散化.

表3 Sample-KDD上的结果(k=1,采用EW进行离散化)Table 3 Results on Sample-KDD(k=1 and using EW for discretization)

表4 Sample-KDD上的结果(k=3,采用EW进行离散化)Table 4 Results on Sample-KDD(k=3 and using EW for discretization)
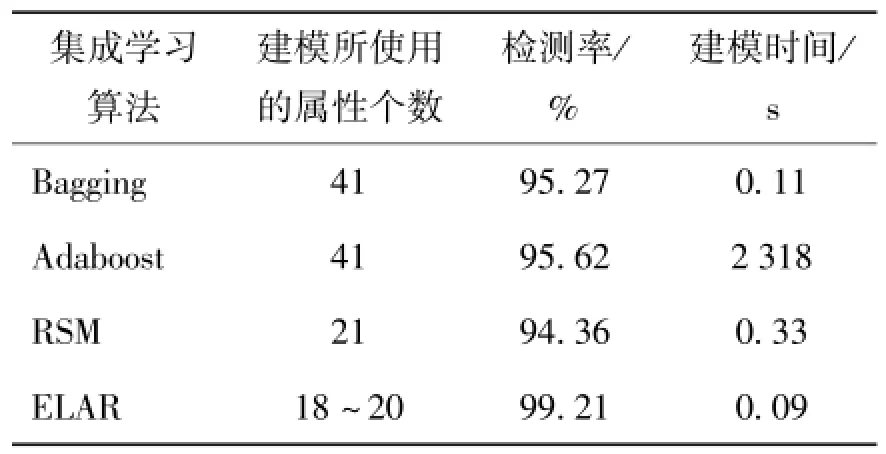
表5 Sample-KDD上的结果(k=5,采用EW进行离散化)Table 5 Results on Sample-KDD(k=5 and using EW for discretization)
从表3~5可以看出,在由EW所离散化的Sample-KDD数据集上,相对于不同k的取值,ELAR的性能总是要好于Bagging、Adaboost和RSM,其中,ELAR的检测率约为99%,其他几种算法的检测率约为95%,因此,可以计算得出,ELAR算法的检测率要比其他算法高4%左右.另外,在4种集成学习算法当中,ELAR的建模时间最短,而Adaboost的建模时间最长.Adaboost算法在建立后一个基学习器的时候需要根据前一个基学习器的学习错误率来改变样本重采样的权重比,属于迭代算法,因此其建模时间相对比较长.
表6~8分别给出了当k取1、3和5时各个集成学习算法在Sample-KDD上的入侵检测结果,其中,EF算法被用来对Sample-KDD进行离散化.

表6 Sample-KDD上的结果(k=1,采用EF进行离散化)Table 6 Results on Sample-KDD(k=1 and using EF for discretization)

表7 Sample-KDD上的结果(k=3,采用EF进行离散化)Table 7 Results on Sample-KDD(k=3 and using EF for discretization)

表8 Sample-KDD上的结果(k=5,采用EF进行离散化)Table 8 Results on Sample-KDD(k=5 and using EF for discretization)
从表6~8可以看出,在由EF所离散化的Sample-KDD数据集上,相对于不同的 k的取值,ELAR的检测率也总是要高于其他3种集成学习算法,另外,ELAR的建模时间均少于其他算法.因此,上述实验结果同样证明了ELAR算法具有较好的入侵检测性能.
5 结论
1)定义了近似约简的概念,采用随机策略和贪心策略相结合的方式实现了近似约简算法.
2)近似约简算法能够将数据集的属性空间划分为多个与原始属性集具有相同或近似分辨能力的属性子集.
3)将基于近似约简的集成学习算法ELAR用于网络入侵检测,实验结果表明:与其他算法相比,ELAR具有更高的检测率和更低的计算开销.
[1]李文斌,刘椿年,钟宁.基于两阶段集成学习的分类器集成[J].北京工业大学学报,2010,36(3):410-419.
LI W B,LIU C N,ZHONG N.Combining classifiers based on two-phase ensemble learning[J].Journal of Beijing University of Technology,2010,36(3):410-419.(in Chinese)
[2]DIETTERICH T G.Machine learning research:four current directions[J].AI Magazine,1997,18(4):97-136.
[3]BUHLMANN P,YU B.Analyzing bagging[J].Annals of Statistics,2002,30(4):927-961.
[4]SCHAPIRE R E.The boosting approach to machine learning:an overview[C]∥MSRI Workshop on Nonlinear Estimation and Classification.New York:Springer,2002: 149-171.
[5]HO T K.Nearest neighbors in random subspaces[C]∥Proceedingsofthe2ndInternationalWorkshoponStatistical Techniques in Pattern Recognition.Heidelberg: Springer,1998:640-648.
[6]HO T K.The random subspace method for constructing decision forests[J].IEEETransactionsonPattern Analysis and Machine Intelligence,1998,20(8):832-844.
[7]BREIMAN L.Random forests[J].Machine Learning,2001,45(1):5-32.
[8]BRYLL R,GUTIERREZ-OSUNA R,QUEK F.Attribute bagging:improving accuracy of classifier ensembles by using random feature subsets[J].Pattern Recognition,2003,36(6):1291-1302.
[9]姚旭,王晓丹,张玉玺,等.基于随机子空间和AdaBoost的自适应集成方法[J].电子学报,2013,41(4):810-814.
YAO X,WANG X D,ZHANG Y X,et al.A selfadaption ensemble algorithm based on random subspace and AdaBoost[J].Acta Electronica Sinica,2013,41(4):810-814.(in Chinese)
[10]蒋宗礼,徐学可.一种基于集成学习与类指示器的文本分类方法[J].北京工业大学学报,2010,36(4): 546-553.
JIANG Z L,XU X K.An ensemble learning and category indicator based text categorizing method[J].Journal of Beijing University of Technology,2010,36(4):546-553.(in Chinese)
[11]GUO Y,JIAO L,WANG S,et al.A novel dynamic rough subspace based selective ensemble[J].Pattern Recognition,2015,48(5):1638-1652.
[12]HU Q H,YU D R,XIE Z X,et al.EROS:ensemble rough subspaces[J].Pattern Recognition,2007,40(12):3728-3739.
[13]PAWLAK Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
[14]PAWLAK Z.Rough sets:theoretical aspects of reasoning aboutdata[M].Dordrecht:KluwerAcademic Publishing,1991:23-65.
[15]谭爱平,陈浩,吴伯桥.基于SVM的网络入侵检测集成学习算法[J].计算机科学,2014,41(2):197-200.
TAN A P,CHEN H,WU B Q.Network intrusion intelligent detection algorithm based on AdaBoost[J]. Computer Science,2014,41(2):197-200.(in Chinese)
[16]徐冲,王汝传,任勋益.基于集成学习的入侵检测方法[J].计算机科学,2010,37(7):217-219.
XU C,WANG R C,REN X Y.Ensemble learning based intrusion detection method[J].Computer Science,2010,37(7):217-219.(in Chinese)
[17]ABDULLA A A,MAMUN B I R.A novel SVM-kNNPSO ensemble method for intrusion[J].Applied Soft Computing,2016,38:360-372.
[18]KAVITHA B,KARTHIKEYAN S,MAYBELL P S.An ensemble design of intrusion detection system for handling uncertainty usingneutrosophiclogicclassifier[J]. Knowledge-Based Systems,2012,28(2):88-96.
[19]陈友,程学旗,李洋,等.基于特征选择的轻量级入侵检测系统[J].软件学报,2007,18(7):1639-1651.
CHEN Y,CHENG X Q,LI Y,et al.Lightweight intrusion setection system based on feature selection[J]. Journal of Software,2007,18(7):1639-1651.(in Chinese)
[20]ACM SIGKDD.The KDD Cup 99 dataset[DB/OL].(1999-10-28)[2015-03-15].http:∥kdd.ics.uci. edu/databases/kddcup99/kddcup99.html.
[21]KUNCHEVA L I,SKURICHINA M,DUIN R P W.An experimental study on diversity for bagging and boosting with linear classifiers[J].Information Fusion,2002,3(4):245-258.
[22]徐章艳,刘作鹏,杨炳儒,等.一个复杂度为max(O(|C||U|),O(|C|2|U/C|))的快速属性约简算法[J].计算机学报,2006,29(3):391-399.
XU Z Y,LIU Z P,YANG B R,et al.A quick attribute reduction algorithm with complexity of max(O(|C||U|),O(|C|2|U/C|))[J].Chinese Journal of Computers,2006,29(3):391-399.(in Chinese)
[23]University of California Irvine.UCI machine learning repository[DB/OL].[2015-03-15].http:∥archive. ics.uci.edu/ml/.
[24]WITTEN I H,FRANK E,HALL M A.Data mining: practical machine learning tools and techniques[M].3rd ed.Burlington:Morgan Kaufmann Publishers,2011: 79-112.
[25]陈仕涛,陈国龙,郭文忠,等.基于粒子群优化和邻域约简的入侵检测日志数据特征选择[J].计算机研究与发展,2010,47(7):1261-1267.
CHEN S T,CHEN G L,GUO W Z,et al.Feature selection of the intrusion detection data based on particle swarm optimization and neighborhood reduction[J]. Journal of Computer Research and Development,2010,47(7):1261-1267.(in Chinese)
(责任编辑吕小红)
Approximate Reducts-based Ensemble Learning Algorithm and Its Application in Intrusion Detection
JIANG Feng1,ZHANG Youqiang1,DU Junwei1,LIU Guozhu1,SUI Yuefei2
(1.College of Information Science&Technology,Qingdao University of Science and Technology,Qingdao 266061,China;2.Institute of Computing Technology,Chinese Academy of Sciences,Beijing 100190,China)
To obtain diverse base learners for construct ensemble learner,the issue of ensemble learning was considered from the perspective of partitioning the attribute space.Through rough set theory,the concept of approximate reduct was defined,and further an approximate reducts-based ensemble learning algorithm was proposed.The method could partition the attribute space of data set into multiple subspaces,and the base learners trained on data sets corresponding to different subspaces had large diversity,which guarantee that the ensemble learner has strong generalization performance.To verify the effectiveness of the algorithm,it was applied to network intrusion detection.Experimental results on the KDD CUP 99 data set demonstrate that compared with the traditional ensemble learning algorithms,the proposed method has higher detection rate and lower computational cost,which is more suitable for the detection of intrusions from the massive and high-dimensional network data.
approximate reducts;ensemble learning;intrusion detection
TP 181
A
0254-0037(2016)06-0877-09
10.11936/bjutxb2015100008
2015-10-07
国家自然科学基金资助项目(61303193);山东省自然科学基金资助项目(ZR2014FM015);山东省高等学校科技计划资助项目(J11LG05)
江峰(1978—),男,副教授,主要从事数据挖掘、粗糙集方面的研究,E-mail:jiangkong@163.net
