阻尼层对水润滑橡胶轴承动态性能的影响

黄　莉，金　勇，刘正林，邹　力

（武汉理工大学 能源与动力工程学院，武汉 430063）



阻尼层对水润滑橡胶轴承动态性能的影响

黄莉，金勇，刘正林，邹力

（武汉理工大学 能源与动力工程学院，武汉 430063）

利用有限元仿真方法在Ansys Workbench中研究阻尼层对轴承模态频率和模态振型的影响。使用Pulse分析平台对轴承振动信号进行采集，应用振动频谱分析方法研究实际运行过程中阻尼层对水润滑橡胶轴承振动的影响。仿真结果表明：与非阻尼轴承相比，阻尼轴承低阶固有频率较低。试验结果表明：在阻尼轴承低阶固有频率附近存在一定的能量集中，但在正常工作转速（0～200 Hz）工况下，不会发生共振；阻尼层能够降低轴承的振动，特别是在高转速、高载荷的工况下减振效果显著。

振动与波；阻尼层；水润滑橡胶轴承；仿真；模态分析；Pulse

在船舶、航空、机械等诸多工程领域，结构振动会带来噪声、降低构件寿命甚至导致构件失效，一直是学者们研究的热点。由高分子聚合物组成的阻尼层，在振动的作用下，其应力和应变存在相位差。这种滞后的运动要克服很大的阻力，能够达到耗散结构能量，抑制构件振动的效果［1］。因此，阻尼层被广泛应用于结构的减振降噪，并且取得了显著的成效。例如将阻尼层应用到波纹管的设计中，制成高阻尼无加强U型减振波纹管，减振性能优于无阻尼波纹管［2］。对于阻尼层在平板结构的应用中，不同的学者使用不同的设计变量［3-4］，对带有阻尼夹层的梁进行结构优化。在这些领域中，阻尼层都对减振降噪做出了贡献。

近年来，水润滑橡胶轴承由于其良好性能在水下航行器上得到广泛应用［5-6］。国内外有很多学者对水润滑橡胶轴承的动态特性进行了研究［7-10］。例如金勇等［11-12］对水润滑橡胶轴承模态的影响因素进行了仿真和试验分析，得出轴承的低阶模态主要受到内衬结构及其材料属性的影响，高阶模态主要受到衬套结构及其材料属性的影响；重庆大学的吴晓金等［13-14］探讨了水润滑轴承的外壳材料对其特征频率的影响，并着重研究了内外层材料结合对谐响应的影响规律。但现有的水润滑橡胶轴承并没有满足人们对水下航行器隐蔽性的需求，很多学者致力于让水润滑橡胶轴承拥有更优秀的振动性能。

上述研究都没有考虑阻尼层对轴承动态特性的影响。考虑到阻尼层在其他结构上良好的减振降噪效果，以及降低水润滑橡胶轴承工作噪声的需求，文中应用Workbench对水润滑橡胶轴承进行有限元模态分析，研究阻尼层对轴承模态频率和模态振型的影响，并通过Pulse分析平台采集非阻尼轴承和阻尼轴承在相同工况下的振动情况，使用振动频谱分析法研究阻尼层的存在对轴承振动带来的影响。

1　有限元模态分析

1.1分析模型

阻尼轴承和非阻尼轴承的区别在于其在非阻尼轴承外包裹一层阻尼材料橡胶，并在阻尼层外装有外衬套，如图1所示。

图1　阻尼轴承剖面图

采用Workbench软件根据水润滑橡胶尾轴承实体模型建立其几何模型。阻尼轴承A1、A2、A3用来对比不同阻尼层长度的影响，轴承材料参数如表1所列，几何参数如表2所列，阻尼层居中布置。

采用实体单元对计算模型进行扫掠网格划分，增加橡胶内衬的网格密度，综合考虑计算精度与规模成本以设置单元尺寸，最终非阻尼轴承模型共包括42 500个单元和209 596个节点，阻尼轴承A3模型共包括48 200个单元和241 796个节点。

模态分析是动力学分析的基础，对系统的动态响应、动载荷的产生与传递以及系统振动的形式等具有重要意义。采用Workbench默认的Block Lanczos迭代法计算水润滑轴承的约束模态，根据实际运行情况，对外衬套外圆柱表面进行全约束，提取轴承前20阶的模态。

1.2模态分析结果

各轴承特征频率计算结果如图2所示。

图2　阻尼层对特征频率的影响

图2表明不同阻尼层对轴承特征频率的影响。根据图2，分析阻尼层对轴承模态频率的影响可以得出：

1）阻尼轴承的各阶模态频率都比非阻尼轴承低，且在模态阶次较低（6阶以下）时，特征频率差异很大，模态阶次较高（6阶以上）时，特征频率差异不再明显。这是由于阻尼层的弹性模量较小，使得整个轴承刚度变小，对轴承的低阶模态造成影响。

2）对于三种不同结构的阻尼轴承，高阶（6阶以上）模态基本一致，低阶（6阶以下）模态差异明显，且阻尼轴承的特征频率随着阻尼层长度的减小而减小，这是因为阻尼层越短，轴承的刚度越小，从而轴承的模态频率越小。

3）非阻尼轴承的低阶（6阶以下）模态频率比阻尼轴承更加集中。

将固有频率结合不同轴承的模态振型进行分析，可以得到如下结论：

（1）非阻尼轴承存在大量相近的固有频率，且振型表现为正交，如第2、3阶频率，第4、5阶频率，为对称模态，来自于模态求解计算中的重根。

表1　轴承材料参数

表2　轴承几何参数/mm

（2）阻尼轴承也存在大量对称模态，5阶以前对称模态分布有差异，5阶以后对称模态分布一致。

（3）各轴承在固有频率接近时的变形非常相似。比如在频率约为634 Hz时，不同轴承的振型如图3所示。

此时，四种轴承都只有橡胶内衬发生变形，最大变形均出现在相邻两个板条的最末端，且每两个变形最大的板条中间都有一个变形很小的板条。轴承板条的变形都发生在轴向，且处于相对位置的板条变形方向相同。

（4）与非阻尼轴承相比，阻尼轴承低阶振型对应的变形范围大。图4为阻尼轴承A3的低阶振型。由图4可见，阻尼轴承A3的低阶振型变形涉及到内衬、内衬套和阻尼层的变形。非阻尼轴承的振型变形范围小，只涉及到轴承内衬，如图3（a）。

2　振动测试试验

在实际运行状态下，轴承固有频率过低可能会导致共振，对固有频率最低的阻尼轴承A3进行振动测试，得到其在正常工作状态下的频谱图，与非阻尼轴承进行对比。

图3　不同轴承振型图

图4　阻尼轴承A3振低阶型图

2.1测试系统

图5为武汉理工大学轴承实验室的SSB-100船舶尾轴承试验样机，图中5为试验轴承，采用液压油缸进行中间加载。加速度传感器安装于试验轴承外壳的中间截面如图中5所示，将振动信号传递给Pulse分析平台，实现对信号的实时分析。

2.2试验台架振动特性

根据转子系统的振动理论，船舶尾轴承试验台架在运转过程中产生振动可能有以下情况：

（1）电机的风机振动，其振动频率一般为旋转轴的基频和风机叶片数的乘积［15］。

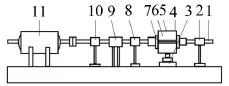
图5　SSB-100船舶尾轴承试验样机

（2）转矩转速仪的振动，原因是转矩转速仪在安装过程中没有校中且其刚度和阻尼小，是试验台的主要振动。

（3）基座松动，由于图5中4和3用油压压紧而不是固接，会产生垂直方向的振动，其随着压力的升高不断减小［16］。

（4）轴系不对中，通过联轴节相连的轴系发生不对中故障的可能性非常大，其二倍转频幅值很大，随着载荷的提高，振动的幅度会逐渐加大，但对轴系运转速度不敏感［18］。

（5）轴系不平衡，即当转子质心和旋转中心不同心时，轴系不平衡会引起振动。

（6）摩擦振动，由于尾轴与尾轴承之间特殊的工作环境，接触面总是存在边界润滑，所以会在中频区产生由干摩擦导致的振动［15］。

2.3振动试验

通过分析台架的振动特性，以及考虑到试验工况主要在中低速范围，参考该台架的振动测试数据，确定其振动能量主要集中在中低频区区域，故选择的测试范围为0～500 Hz。由于轴承垂向振动比水平方向更加明显，所以对垂直方向的振动进行测试分析。

根据船舰的常用工作转速和负荷，设定工况为：（1）负荷：0.2 MPa、0.3 MPa、0.4 MPa；

（2）转速：50 r/min～200 r/min。

2.4随转速变化的振动结果

在加载压力为0.4 MPa时，对两种轴承进行升速测试，采集的阻尼轴承A3的垂向频谱图如图6所示，非阻尼轴承的垂向频谱图如图7所示。由图6和图7可以看出：

图6　阻尼轴承A3垂向方向频谱图（0.4 MPa）

（1）加载压力为0.4 MPa时，阻尼轴承的振动幅值低于非阻尼轴承的振动幅值。

（2）随着转速的升高，两种轴承在垂直方向上的振幅均会增加，非阻尼轴承的增幅大于阻尼轴承。

（3）轴承在外部激励作用下发生受迫振动［17］，其在图6和图7中的250 Hz处振幅不随转速发生变化，经振动分析可得到这是由液压油缸的激励引起的［18］，在载荷为0.4 MPa时，非阻尼轴承的响应明显大于阻尼轴承A3。

2.5随负荷变化的振动结果

在船舶常用转速100 r/min工况下，改变试验载荷，得到两种轴承的振动情况随载荷变化的频谱图如图8—图13所示。

为了更清晰地进行对比，列出0～500 Hz频段内振幅总有效值如表3所示，在250 Hz处受迫振动的响应如表4所示。

图7　非阻尼轴承垂向方向频谱图（0.4 MPa）

图8　阻尼轴承A3垂向方向频谱图（0.2 MPa）

图9　非阻尼轴承垂向方向频谱图（0.4MPa）

图10　阻尼轴承A3垂向方向频谱图（0.3 MPa）

结合图8—图13和表3可以看出。

（1）随着加载压力的升高，两种轴承的振幅都有一定程度的上升。非阻尼轴承总有效值增幅大于阻尼轴承A3。

图11　非阻尼轴承垂向方向频谱图（0.3 MPa）

图12　阻尼轴承A3垂向方向频谱图（0.4 MPa）

图13　非阻尼轴承垂向方向频谱图（0.4 MPa）

表3　0～500 Hz范围内振幅总有效值/（mm/s2）

表4　250 Hz处受迫振动响应（mm/s2）

（2）不同的加载压力下，阻尼轴承A3的振动能量分散程度均大于非阻尼轴承，表现为振动幅值峰值分布分散。

（3）不同的加载压力下，非阻尼轴承振幅的总有效值都大于阻尼轴承A3。

（4）在60 Hz和210 Hz频率附近，阻尼轴承A3的峰值高于非阻尼轴承。

由表4可以得到：在特定激励（250 Hz）的受迫振动响应方面，载荷为0.2 MPa时，非阻尼轴承的振幅小于阻尼轴承A3，随着载荷的上升，非阻尼轴承的响应迅速上升，载荷为0.4 MPa时，非阻尼轴承的振幅超过阻尼轴承A3。

2.6试验结果分析

（1）转速升高时，阻尼轴承由于内阻尼大，对振动有一定衰减作用，故其振幅增幅较非阻尼轴承要小。

（2）由于阻尼轴承的刚度较小，对轴颈变形有良好的适应性，能够更加均匀地与轴颈进行接触，故振动能量分布比较分散。但是阻尼轴承的低阶固有频率低，60 Hz和210 Hz接近阻尼轴承的低阶固有频率，发散的振动能量存在向低阶固有频率附近集中的趋势，故这两处的频率峰值高于非阻尼轴承。

（3）垂向负载较小时，阻尼轴承在油缸激励（250 Hz）下响应幅值比非阻尼轴承高，随着负载压力的增大，轴线变形对轴承振动带来的影响变大，由于阻尼轴承具有一定的调心作用，缓解了由于载荷变大带来的轴线变形，故其在负载较大时的振动幅值明显低于非阻尼轴承。

3　结语

（1）阻尼轴承的固有频率比非阻尼轴承要低，低阶模态频率差异大，由于阻尼轴承对振动的衰减作用，实际使用过程中低阶固有频率不会引起强烈的振动。

（2）阻尼层能够分散轴承的振动能量，但分散的能量会向低阶固有频率附近集中，使得阻尼轴承在其低阶固有频率附近处的峰值比非阻尼轴承略大。

（3）转速较低或者载荷较小的情况下，阻尼轴承降低振动的优势不明显，且载荷较小时阻尼轴承对外界激励的响应（本试验只验证了对250 Hz外界激励的响应）可能比非阻尼轴承大，在转速较高或者负载较大的情况下，阻尼轴承能更大程度降低轴承的振动，在实际使用过程中，应该根据运行工况和对轴承振动的要求综合考虑是否采用阻尼轴承。

［1］黄志诚，秦朝烨，褚福磊，等.附加粘弹阻尼层的薄壁构件振动问题研究综述［J］.振动与冲击，2014，（7）：105-113.

［2］钟玉平，陈同彪.高阻尼无加强U形减振波纹管研究［J］.压力容器，2005，（7）.

［3］ LI JINQIANG，YOSHIHIRO NARITA.The effect of aspectratiosandedgeconditionsonthe optimal damping design ofthinsoftcore sandwichplates and beams［J］.Journal of Vibration and Control，2014，2（20）:266-279.

［4］ MAOÛT N L，VERRON E，BÉGUÉ J.Simultaneous geometricalandmaterialoptimaldesignofhybrid elastomer/compositesandwichplates［J］.CompositeStrdctures，2011，93（3）:1153-1157.

［5］DE KRAKER D，VAN OSTAYEN R A J，RIXEN D J. Calculation of Stribeck curves for（water）lubricated journal bearings［J］.Tribology International，2006，403.

［6］周欢欢，俞强，李天匀，等.水润滑橡胶轴承板条型式及硬度分区对接触性能影响研究［J］.船舶工程，2015（4）：25-28+41.

［7］彭晋民，朱志宏，王家序.水润滑轴承的研究现状及展望［J］.润滑与密封，2004（5）：124-126+130.

［8］LITWIN，W.Experimental research on water lubricated three layer sliding bearing with lubrication grooves in the upper part of the bush and its comparison with a rubber bearing［J］.Tribology International，2015-82:153-161.

［9］NAJAR，F A，HARMAIN G A.Thermal effects for conventional and water-cooled thrust bearing using finite difference method:comparative analysis［J］.International Journal of Precision Technology，2015，5（1）:14-26.

［10］金勇.水润滑尾轴承-尾轴系统的横向/摩擦耦合振动研究［D］.武汉：武汉理工大学，2014.

［11］金勇，田宇忠，刘正林.水润滑橡胶尾轴承模态影响因素分析［J］.润滑与密封，2011（9）：10-13+23.

［12］金勇，田宇忠，刘正林，等.橡胶艉轴承的试验模态分析［J］.噪声与振动控制，2012，32（1）：34-38.

［13］吴晓金，王家序，肖科，等.水润滑轴承的动态特性研究［J］.润滑与密封，2008（2）：21-25.

［14］吴晓金，王家序，肖科，等.水润滑轴承的动态仿真分析［M］.系统仿真学报，2009，21（13）：4167-4170.

［15］杨长江.机械振动谱图分析诊断［J］.后勤工程学院学报，2006，2：54-57.

［16］谢三毛.基于频谱分析的离心压缩机故障诊断［J］.矿山机械，2006（5）：108-109.

［17］陈之炎.船舶推进轴系振动［M］.上海：上海交通大学出版社，1987：281.

［18］金勇，刘正林.水润滑橡胶艉轴承动态性能的试验与分析［J］.噪声与振动控制，2011，31（4）：64-67.

Influence of Damping Layer on Dynamic Performance of Water-lubricated Rubber Bearings

HUANGLi，JINYong，LIU Zheng-lin，ZOULi

（School of Power and Energy，Wuhan University of Technology，Wuhan 430063，China）

Effects of damping layer on modal frequency and modal shape of water-lubricated rubber bearings are studied by means of finite element method in Ansys Workbench.The Pulse system is used to collect the vibration signals of the bearings.The vibration spectrum analysis method is employed to analyze the influence of the damping layer on the vibration of the water-lubricated rubber bearings.The simulation results show that comparing with non-damping bearings，the damped bearings have lower low-order natural frequencies.The test results show that for the damped bearing，there are some energy concentrations near the low-order natural frequencies，but resonance does not occur under normal operating speed（0-200 Hz）.The vibration of bearing can be reduced by the damping layer，especially under high speed and high loading conditions.

vibration and wave；damping layer；water-lubricated rubber bearing；simulation；modal analysis；Pulse

O422.6

ADOI编码：10.3969/j.issn.1006-1335.2016.04.007

1006-1355（2016）04-0032-06

2016-01-26

国家自然科学基金资助项目（51379168）

黄莉（1992-），在读研究生，湖北省荆州市人，研究方向为轴承减振降噪分析。E-mail:415540616@qq.com

金勇（1976-），研究生导师，四川省德阳市人，副教授。E-mail:jy761121@163.com