约束方式对橡胶高频振动测试结果的影响

郝　敏，陈高升，裴高林，苏正涛

（中国航空工业集团公司 北京航空材料研究院 减振降噪材料及应用技术航空科技重点实验室，北京 100095）



约束方式对橡胶高频振动测试结果的影响

郝敏，陈高升，裴高林，苏正涛

（中国航空工业集团公司 北京航空材料研究院 减振降噪材料及应用技术航空科技重点实验室，北京 100095）

针对不同约束方式对黏弹性材料高频振动性能的影响开展研究，比较2 000 Hz～6 000 Hz频率范围内不同约束方式对阻尼梁振动性能的相干性，并提取2 000 Hz～6 000 Hz内不同阶数的模态，采用有限元方法对不同约束方式阻尼梁的振动试验进行仿真。将模态试验结果与出现共振峰最多的中间节点的速度传递率进行对比，结果表明：两端固支竖直放置工况的相干性最优，两端固支竖直放置工况的试验结果与一端固支竖直放置工况相比与仿真结果更吻合，有关结论为用振动梁法在高频振动条件下测试黏弹性橡胶材料时约束方式的选择提供参考依据。

振动与波；传递函数；约束方式；相干性；模态

黏弹性阻尼材料一般是以聚合物存在的高分子，其阻尼机理是阻尼材料在受到交变应力作用下，应变滞后于应力，有一部分功损耗掉转化为热，滞后现象越严重，材料的阻尼性能越好，因此可利用高分子材料的粘弹阻尼特性将振动机械能转化成热能消耗掉以达到减振降噪的目的［1］。黏弹性阻尼材料已设计成自由阻尼层和约束阻尼层结构以及阻尼吸振块结构等，在航空、航天、汽车、船舶等诸多领域均得到了广泛的应用［2］。

高聚物黏弹性材料的阻尼值用损耗因子β表征，损耗因子β是反映高聚物粘弹性材料振动特性的重要指标，在研制新型黏弹性材料、判断调整其配方时，需要测定阻尼材料的损耗因子，但由于高聚物黏弹性材料的β是温度和频率的函数，所以不能采用橡胶工业中常用的测试方法来测试，而必须用专用设备来测定［3-5］。目前国内外已设计研制出的测试方法和装置主要有自由衰减法、正弦激励法、相位法和振动梁法。

自由衰减法和正弦激励法装置简单，测量精度差，相位法虽说测量精度高，但价格昂贵，且1 000 Hz以上的模量和损耗因子只能通过拟合的方法得出而非实际测量。振动梁法是应用较广的一种方法，至今美国宇航局仍采用此法测阻尼材料性能。该方法根据振动模态分析理论及梁的动力分析理论公式，利用振动梁共振后突然释放产生模态衰减振动的原理，测定振动梁的幅频曲线或传递函数曲线，可得到所需频段振动梁的固有频率及相应的结构损耗因子，再根据理论公式求得各频率下阻尼材料本身的剪切模量G'和损耗因子β［6］。这种方法符合实际使用工况，测试精度高。试验人员在进行模态试验时一般考虑使结构件处于自由状态，可获得系统无约束时的模态，但对于大多数工程实际情形，所谓自由状态还是要通过某种支撑来实现的。不同的支撑决定不同的约束方式，约束方式的选择对结构件模态试验的真实性、准确性起到关键作用。文中通过传递函数对不同约束方式振动梁的相干性进行比较，运用模态分析技术和有限元方法对不同约束方式下的振动梁进行仿真计算，再与实际测试结果进行对比。在2 000 Hz～6 000 Hz的范围内选择最合适的约束方式进行振动梁法实验，确定出更接近于实际使用工况的约束方式，为高频振动梁法约束方式的选择提供参考依据，进而为黏弹性材料在高频条件下的研究提供测试平台。

1　实验

1.1实验材料

ASTME 756中推荐使用的振动梁宽度10 mm，试样自由端长度180 mm～250 mm，厚度1 mm～3 mm。实验时选择振动梁长为200 mm，宽为10 mm，振动梁总厚度为2.3 mm。整个基梁采用金属铝，中间夹有阻尼材料，该实验采用的阻尼材料为氯化丁基橡胶。

1.2实验方法

振动梁法高频振动阻尼测试装置由激振系统、测振系统、采集和分析系统和工装夹具组成，该装置原理图如图1。

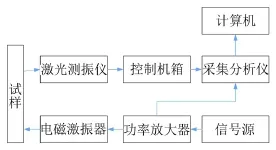
图1　振动梁法高频振动阻尼测试装置原理图

激振系统由信号源、功率放大器、电磁激振器组成，通过激振系统对振动梁试样进行激励；测振系统由激光测振仪和控制机箱组成，激光测振仪相当于速度传感器用于对试样振动的速度信号进行测量，利用光学干涉原理激光器发出一定频率的偏振光，通过声光调制器具有一定频移聚焦被测物表面，物体振动会引起多普勒频移，系统收集偏振光聚在传感器上并在其表面产生干涉，干涉信号携带了物体的振动信息，再由控制机箱将频移信号转换为速度信号；采集和分析系统由双通道采集分析仪和计算机组成，用于收集信号并进行后处理。信号源发出的信号经功率放大器放大后传给电磁激振器对试样进行激励，激光测振仪发出的激光信号打在试样上对试样振动的速度信号进行测量，双通道采集分析仪同时采集功率放大器的激励信号和控制机箱的响应信号经转换并处理后传给计算机，计算机通过测试软件对激励和响应信号进行传递函数分析，得到幅频曲线、相频曲线和相干曲线。

2　结果与分析

2.1不同约束方式相干性比较

比较不同约束方式的相干性，图2-图4为三种不同的约束方式。

图2　两端固支竖直放置

图3　一端固支竖直放置

图4　一端固支水平放置

相干性的好坏直接反映了测试结果的准确性，相干性好说明整个夹持部分受环境影响包括夹持部分本身的干扰小，相反相干性差说明外界干扰大［7］。影响相干性的因素很多，有振动梁本身质量、螺丝松紧、外界环境的影响等等。从三种约束方式相干性的测试结果得出两端固支竖直放置相干性最好，一端固支水平放置相干性最差，一端固支竖直放置相干性居中。一端固支水平放置相干性差的原因是振动梁本身质量对相干性产生了影响，所以为避免振动梁质量的影响将试样竖直放置，再进一步比较两端固支竖直放置和一端固支竖直放置这两种约束方式。

2.2试验与仿真

2.2.1模态试验

采用一端固支法和两端固支法测试梁的振动特性。将振动梁设20点，均分19份。激振器固定在第1点，也就是圆孔约束端，在2 000 Hz～6 000 Hz的频率范围内进行扫描，一次扫描时间为30 s，共扫描2次，同时激光测振仪发出的激光打在第1点的位置，测量这点的速度响应信号。保持激振位置不变，移动测振点位置，激光依次从第1点打到第20点，连续测量20点的随机响应信号，这种测法为SISO测量法，这20点的传递函数即包含整个振动梁进行模态分析所需要的全部信息。

进入模态分析模块，对20点进行传递函数分析，建立振动梁模型并输入约束，约束的方向与振动方向一致，再进行模态分析计算，可得到速度传递率、频率、阻尼的关系和振型［8］。

2.2.2试验与仿真比较

为了验证约束方式对梁振动特性的影响，采用有限元方法对不同约束方式梁的振动特性进行仿真，并将仿真结果与试验结果进行对比。采用Ansys软件对不同约束方式下梁的振动进行谐响应分析，得到振动方向与梁厚度方向一致的主振型及对应的固有频率，为了便于与试验结果进行比较，只提取2 000 Hz～6 000 Hz下不同阶数的模态，并将出现共振峰最多的中间节点的速度传递率与试验结果进行对比［9］。

振动梁有限元模型如图5、图6所示，金属铝片和橡胶均采用六面体网格，在厚度方向的单元数均为2。模拟两端固支条件梁的振动试验时，将端部约束区域内的节点进行全约束，约束圆孔约束端内节点水平方向和竖直方向的位移，进行谐响应分析时，在圆孔约束端的中心节点上施加单位激励载荷。模拟一端固支条件梁的振动试验时，只约束圆孔约束端内节点水平方向和竖直方向的位移，谐响应分析的激励方式与两端固支的相同。有限元分析时，首先进行模态分析，得到梁在2 000 Hz～6 000 Hz内的各阶模态及固有频率，然后对该频段内的模态进行扩展分析，最后进行谐响应分析［10］。

由于试验测试的是振动方向与厚度方向一致的梁的振动，仿真分析时只关心该方向梁的主振型，不同约束方式仿真计算得到的主振型及其固有频率如图7-图8所示。

从图7、图8可以看出，一端和两端固支条件下，在2 000 Hz～6 000 Hz内与厚度方向一致的主振型均有3阶，其中一端固支时，在11阶模态振型（2 936 Hz）、16阶模态振型（5 554 Hz）中梁的中间节点处在共振峰的位置，两端固支时在第5阶模态振型（2 180 Hz）、第9阶模态振型（3 754 Hz）中梁的中间节点处在共振峰的位置，中间节点出现共振峰的次数最多，因此选取中间节点的速度传递率与试验结果进行比较。

一端固支条件下和两端固支条件下振动梁的中间节点对激励点的速度传递率的试验结果与仿真结果比较如图9、图10所示。

图5　一端固支约束

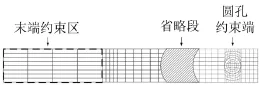
图6　两端固支约束

图7　一端固支条件下厚度方向的主振型

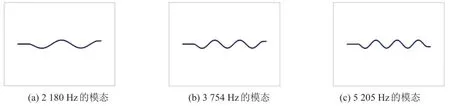
图8　两端固支条件下厚度方向的主振型

图9　一端固支约束条件下中间节点速度传递率的试验与仿真结果比较

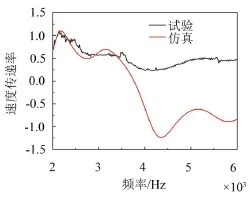
图10　两端固支约束条件下中间节点速度传递率的试验与仿真结果比较

由图9可以看出，在2 000 Hz～6 000 Hz范围内，一端固支条件下，振动梁中间节点的速度传递率在2 060 Hz、3 480 Hz处出现两个共振峰，由有限元计算得到的传递率只在2 000 Hz左右出现了一个较明显的共振峰，从模态振型的结果来看，理论上在11阶振型（2 936 Hz）、16阶振型（5 554 Hz）中间节点的速度传递率均应存在共振峰，从比较的结果可看出理论计算结果与试验结果存在较大出入。

由图10可以看出，在2 000 Hz～6 000 Hz范围内，两端固支条件下，试验测得振动梁中间节点的速度传递率在2 148 Hz、3 480 Hz处出现两个明显的共振峰，在5 560 Hz出现的共振峰不明显，由有限元计算得到的传递率在2 180 Hz、3 152 Hz、5 152 Hz出现3个较明显的共振峰，共振峰所对应的3阶固有频率与试验结果基本一致，在2 000 Hz～3 500 Hz范围内，试验数据与仿真数据吻合良好，在3 500 Hz～6 000 Hz范围内，仿真数据与试验数据趋势基本一致。

3　结语

（1）通过传递函数比较两端固支竖直放置、一端固支竖直放置、一端固支水平放置这三种不同约束方式的相干性，结果表明，两端固支竖直放置条件下的相干性＞一端固支竖直放置条件下的相干性＞一端固支水平放置条件下的相干性。

（2）提取2 000 Hz～6 000 Hz下不同阶数的模态，采用有限元方法对不同约束方式下阻尼梁的振动试验进行仿真，将出现共振峰最多的中间节点的速度传递率与试验结果进行对比，结果表明：两端固支竖直放置比一端固支竖直放置的试验结果与仿真结果更吻合，因此在高频激励下采用两端固支竖直放置这种约束方式的试验方法更准确，测试结果更接近工程应用实际。

［1］戴德沛.阻尼减振降噪技术［M］.西安：西安交通大学，2007.

［2］黄微波，刘超，黄舰.高分子阻尼材料研究进展及发展趋势［J］.材料导报，2012，26（11）：134-139.

［3］徐丰辰，李洪林，刘福.阻尼材料动态阻尼系数的测定［J］.汽车胶粘剂研究与运用，2013，9：73-77.

［4］ MADIGOSKY W M，LEE G F.Improved resonance technique for material characterization［J］.J.Acoust.Soc. Am.，1983，73:1374-1377.

［5］ GARRETT S L.Resonant acoustic determination of elastic moduli［J］.J.Acoust.Soc.Am.，1990，88:210-221.

［6］裴高林，米志安，苏正涛，等.约束阻尼材料性能测试方法的探讨［J］.噪声与振动控制，2008，28（3）：156-159.

［7］安木金，李舜酩，张袁元，等.多相关子系统输入中输入的相干性分析［J］.中国机械工程，2010，11（21）：2609-2613.

［8］李峰，王波，张洪欣.175 m散货船局部结构的模态分析［J］.噪声与振动控制，2010，30（5）：67-70.

［9］陈高升.冰箱压缩机系统振动传递率预估与振动特性研究［M］.西安：西安交通大学，2007.

［10］鲍怀谦，韩宝坤，符俊杰，等.敷设粘弹性材料的溜槽的试验模态分析［J］.噪声与振动控制，2010，30（1）：157-160.

Influence of Constraint Condition on the Results of High-frequency Vibration Test of Rubber

HAOMin，CHEN Gao-sheng，PEI Gao-lin，SU Zheng-tao

（Aviation Key Laboratory of Science and Technology on Materials andApplication Research for Vibration and Noise Reduction，Beijing Institute ofAeronautical Materials，Beijing 100095，China）

The influence of different constraint conditions on the high-frequency vibration performance of viscoelastic materials is studied.The coherences between the different constraint conditions and the vibration properties of a damping beam are compared by transfer function method in 2 000 Hz-6 000 Hz frequency range.Vibration damping tests under different constraint conditions of the beam are simulated by the finite element method.The simulation results of the speed transfer rates at the intermediate nodes of the most formants are compared with those of the experiments.It shows that the simulation result is closer to the test result for the damping beam with both ends clamped than that for the damping beam with only one end clamped.This work provides a reference for selection of constraint conditions in the high-frequency vibration tests of rubber vibrating beams.

vibration and wave；transfer function；constraint condition；coherence；modal

O327文献表示码：ADOI编码：10.3969/j.issn.1006-1335.2016.04.042

1006-1355（2016）04-0198-04

2016-03-08

郝敏（1984-），女，河北省保定市人，硕士，工程师，主要研究方向为特种橡胶材料和材料试验方法。E-mail:haomin_mail@163.com