构造法解一类关于f′(x)的抽象函数问题

江苏省徐州市第一中学　(221140)

许　丽



构造法解一类关于f′(x)的抽象函数问题

江苏省徐州市第一中学(221140)

许丽

构造法是指当解决某些数学问题使用通常方法按照定向思维难以解决问题时，应根据题设条件和结论的特征、性质，从新的角度，用新的观点去观察、分析、理解对象，牢牢抓住反映问题的条件与结论之间的内在联系，运用问题的数据、外形、坐标等特征，使用题中的已知条件为原材料，运用已知数学关系式和理论为工具，在思维中构造出满足条件或结论的数学对象，从而使原问题中隐含的关系和性质在新构造的数学对象中清晰地展现出来，并借助该数学对象方便快捷地解决数学问题的方法．

导数的作用是研究函数的性质．当导数大于0时，函数单调增，当导数小于0时，函数单调减．倘若不等关系是建立在导数f′(x)与非零常数、甚至是函数之间，那就不能直接判断函数f(x)的单调性了．这类问题又该如何处理呢？下面，笔者就以近来的考题为例归类解析，就教于同行．

一、与其他函数不等构造和、差

导数f′(x)与其他函数(包括常函数)构成的不等关系作条件，可以构造f(x)与其他函数的和、差函数，从而获得与f(x)相关的新函数的性质．

例1(2015年福建理科卷10)若定义在R上的函数f(x)满足f(0)=-1，其导函数f′(x)满足f′(x)>k>1，则下列结论中一定错误的是().

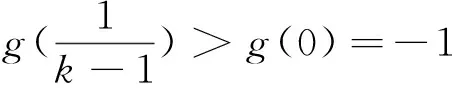
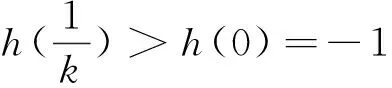
例2(2015届重庆市十八中高三10月测试)

定义在R上的函数f(x)满足f(-x)+f(x)=2x2，当x>0时，f′(x)<2x，若f(m)-f(4-m)-8m+16≥0，则实数m的取值范围为_________．

解析：构造函数g(x)=f(x)-x2，当x>0时，有g′(x)=f′(x)-2x<0，所以函数g(x)在(0，+∞)上单调减．又g(x)+g(-x)=f(x)+f(-x)-2x2=0，所以函数g(x)是奇函数，因此g(x)在R上是单调减函数．

不等式f(m)-f(4-m)-8m+16≥0可化为f(m)-m2≥f(m-4)-(4-m)2，即g(m)≥g(4-m)，所以m≤4-m，解得m≤2．

二、与原函数不等构造积、商

两函数积、商运算的求导法则中会同时出现导函数与原函数，所以导数f′(x)与原函数f(x)构成的不等关系作条件时，可以构造f(x)与其他函数的积、商函数．

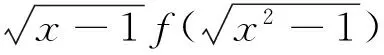
解析：构造函数g(x)=xf(x)，则g′(x)=f(x)+xf′(x)>0，所以函数g(x)在R上是单调增函数．

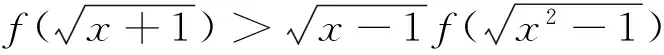
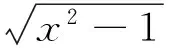
A．(0，+∞)B．(-∞，0) ∪(3，+∞)

C．(-∞，0) ∪(0，+∞)D．(3，+∞)

例5(2015年高考全国新课标Ⅱ卷)设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(-1)=0，当x>0时，xf′(x)-f(x)<0，则使得f(x)>0成立的x的取值范围是().

A．(-∞，-1) ∪(0，1)

B．(-1，0) ∪(1，+∞)

C．(-∞，-1) ∪(-1，0)

D．(0，1) ∪(1，+∞)

例6设函数f(x)的导函数为f′(x)，对任意x∈R，都有f′(x)>f(x)，则().

A．3f(ln2)> 2f(ln3) B．3f(ln2)=2f(ln3)

C．3f(ln2)<2f(ln3)

D．3f(ln2)与2f(ln3) 的大小不确定

例7(2016届甘肃省第一次高考诊断考试理科12)已知函数f(x)的导函数为f′(x)，若∀x∈(0，+∞)，都有xf′(x)<2f(x)成立，则().

三、综合问题适当构造

以上可见，能构造出积、商函数的问题条件皆为两项的不等式形式，一项含f(x)，另一项含f′(x)．那么更为复杂的不等关系呢？

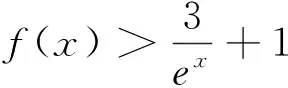
A．(0，+∞)B．(-∞，0) ∪(3，+∞)

C．(-∞，0) ∪(0，+∞)D．(3，+∞)

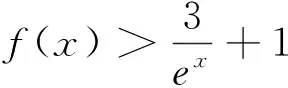
例9已知函数f(x)是定义在(-∞，0) 上的可导函数，其导函数为f′(x)，且有xf′(x)>x2+2f(x)，则不等式4f(x+2014)-(x+2014)2f(-2)>0的解集为().

A．(-∞，-2012)B．(-2012，0)

C．(-∞，-2016) D．(-2016，0)