构造一元二次方程 巧解定值定点问题

广东省广州市增城区增城中学　(511300)

李　雷



构造一元二次方程巧解定值定点问题

广东省广州市增城区增城中学(511300)

李雷

解析几何综合问题的解法一般都是设方程、联立,利用韦达定理、计算、化简等.过程看似常规,学生却望而生畏,考试得分有限.而解析几何综合试题中的定值、定点问题一直是考试的热点和重点,构造恰当的一元二次方程,利用其有关性质,可使一些看似难以解决的问题顺利获得解决.

一、 定点问题

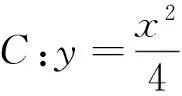
(1) 当k=0时,分别求C在点M和N处的切线方程；

(2) y轴上是否存在点P使得当k变动时,总有∠OPM=∠OPN?说明理由.

解：(1)略.

(2)设P(0，m),直线PM，PN的斜率分别为k1,k2,∵∠OPM=∠OPN，∴k1+k2=0.

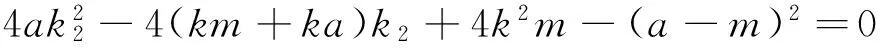
命题3在直角坐标系中,抛物线C:x2=2py(p>0)与直线l:y=kx+m交于M，N两点.直线PM，PN的斜率分别为k1，k2，若k1+k2=0，则点P为定点(0，n)，并且m+n=0.

下面给出命题1的证明：

当直线l与x轴平行时,此时M，N关于y轴对称,∴点P在y轴上.

设点P(0，n),PM:y=k1x+n,联立

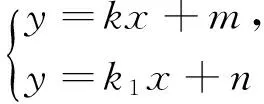
因为点M在椭圆C上,将点M代入椭圆方程b2x2+a2y2=a2b2得

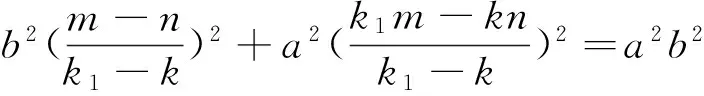
(a2m2+a2b2)k12-(2kmna2-2ka2b2)k1-(a2n2+a2b2)k2-b2(m-n)2=0①.

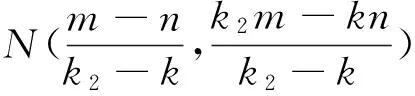
综合①②可知k1，k2为下面方程的两个根:

(a2m2+a2b2)x2-(2kmna2-2ka2b2)x+(a2n2+a2b2)k2-b2(m-n)2=0，根据韦达定理可知

二、定值问题

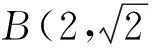
(1) 求椭圆C的方程；

(2) 以MN为直径的圆是否经过定点？若经过,求出定点的坐标；若不经过,请说明理由.

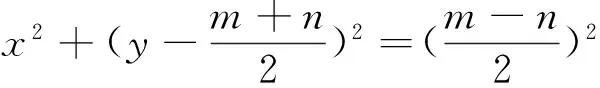
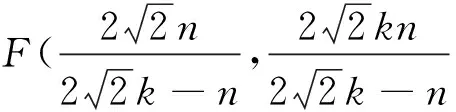
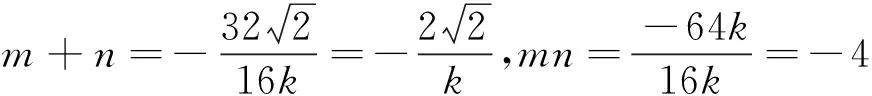
三、 应用

(1) 求椭圆的方程；

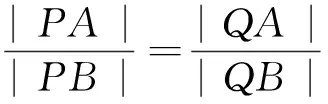
四、感悟

`定值定点通常是指在一定的情境下,不随其他条件的改变而改变的量.因此“特值探路”不可或缺．正是有了“特值探路”,才使得解题方向明确、目标清晰．适当构造一元二次方程,可极大地减少解题的运算量,使问题迎刃而解,而且解答别具一格,耐人寻味！也为课堂教学添色增值.与此同时,培养了学生解题的信心,消除了学生畏难情绪,激发了学生创新意识.