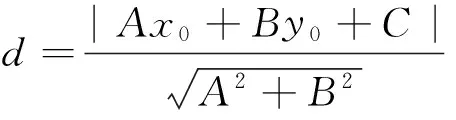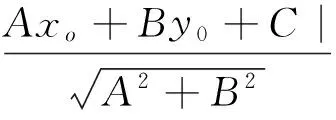柯西不等式在解题中的应用
2016-08-26江苏省连云港市郁林中学222346
中学数学研究(江西) 2016年8期
江苏省连云港市郁林中学 (222346)
张雪峰
柯西不等式在解题中的应用
江苏省连云港市郁林中学(222346)
张雪峰

1在代数中的应用
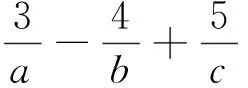
解:将4a2-2ab+4b2-c=0变形为2c=3(a+b)2+5(a-b)2,由柯西不等式得
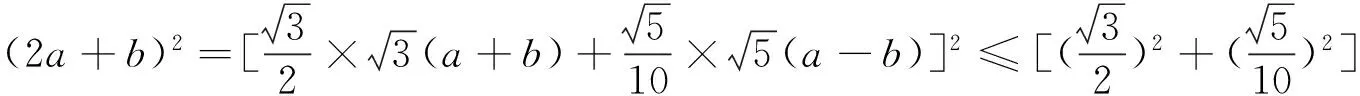
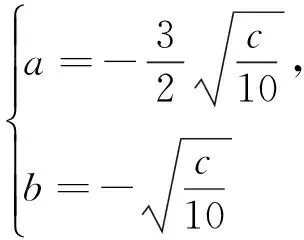
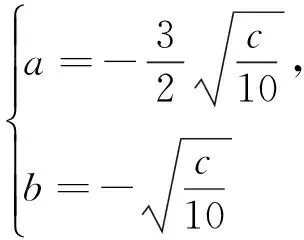

例2设x、y为实数,若x2+y2+xy,则x+y的最大值是_________.
解:将原方程组中的两个方程相加得 (2x)2+(3y+3)2+(z+2)2=108,将第一个方程可变形为2x+(3y+3)+(z+2)=18,由柯西不等式得[(2x)2+(3y+3)2](12+12)≥[2x+(3y+3)]2,所以 2[108-(z+2)2]≥[18-(z+2)2]2,所以 (z-4)2≤0,解得z=4,由柯西不等式成立的条件可得x=3,y=1,所以x=3,y=1,z=4.
2在函数中的应用
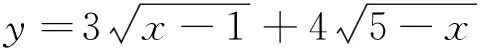

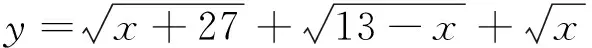
3在三角函数中的应用

解:由柯西不等式,得

4在不等式中的应用
例7已知定义在R上的函数f(x)=|x+1|+|x-2|的最小值为a.
(1)求a的值;
(2)若p,q,r是正实数,且满足p+q+r =a,求证p2+q2+r2≥3.
解:(1)略.
(2)由(1)知p+q+r =3,又因为p,q,r是正实数,所以由柯西不等式得(12+12+12)(p2+q2+r2)≥(1·p+1·q+1·r)2=(p+q+r)2=9,即p2+q2+r2≥3.
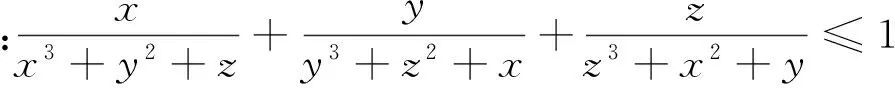
解:由柯西不等式知


5在圆锥曲线中的应用
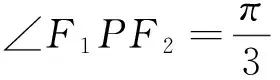
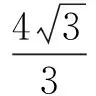
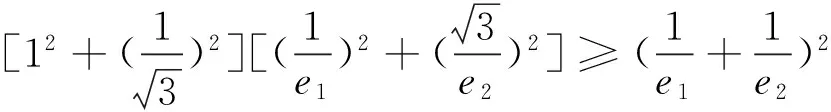
6在平面几何中的应用
例10在平面直角坐标系中,已知点A(1,-2),B(4,0),P(a,1),N(a+1,1),则当四边形PABN的周长最小时,过三点A,P,N的圆的圆心坐标是_________.

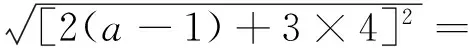

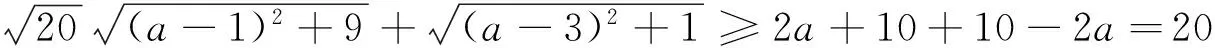
7巧证课本上的公式