以问题为核心,建构生成性复习课堂

◇ 江苏 郑 艳

以问题为核心,建构生成性复习课堂

◇ 江苏 郑 艳

问题是思维的起点,在复习教学中如何以问题为核心,引导学生思考、探究、分析、总结、归纳,运用所学知识自主解决问题、提高复习教学效果是当前广大教师们应思考的重要课题之一.对此,笔者结合自身教学实践,略谈几点看法和体会,以供参考.

1 巧设有效问题情境,在问题分析和自主探究中生成智慧

巧设问题情境,引导学生自主分析、探究和解决问题是突破重、难点的有效手段.在高中数学生成性复习教学中,教师要注意从实际出发,通过围绕教学目标、紧扣教学内容、精心设计问题情境、提出有效问题等,引导学生积极自主地展开思考、探究、讨论、理解等活动,从而让学生在一系列的问题情景中去理解所学知识,体会解决问题的方法,促进学生智慧的成长和能力提升.

例如,在复习“函数概念”时,为了深化巩固学生对函数概念的整体性理解和把握,笔者通过设计“想一想”“练一练”等问题情境,启发学生积极思考、自主分析、探究和解决问题,从而唤起学生问题意识,激发学生的探究动机,促使学生有效复习.

1)想一想.

同学们,我们知道函数的本质是从一个非空数集到另一个非空数集的特殊对应,是由定义域、对应关系、值域3要素构成的一个整体.

例1 已知A＝{x|0≤x≤2},B＝{y|0≤y≤2},下列各图中能表示从A到B的函数是( ).

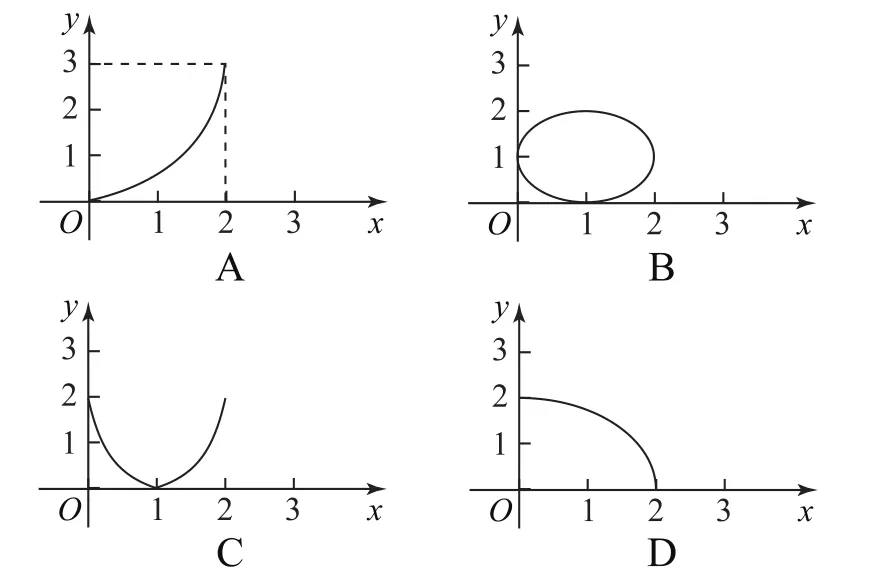
选项A中函数的值域为{y|0≤y≤3}≠B,故应予以排除.选项B中当x∈{x|0＜x＜ 2}时,会有2个y值与其对应,不满足映射定义中的唯一性,故排除.选项C中定义域为A、值域为B,符合条件.选项D中函数的定义域为{x|0＜x≤2}≠A,故应排除.

2)练一练.

例2 判断下列函数中哪个函数与函数y＝x为同一函数( ).

判断2个函数是否为同一函数,关键在于其定义域和对应法则是否完全一致.因此,经过分析,该题只有选项C符合要求.

2 积极鼓励勤思善问,在主动质疑和交流互动中生成智慧

在高中复习教学过程中,教师要为学生搭建自由表达、展现个性、激励创新的平台,以问题为载体,为学生提供自主参与、合作探究、质疑反思、交流互动的时间和空间,积极鼓励学生勤思善问、生疑质疑,围绕问题大胆发表自己的见解,提出自己的疑惑,追根溯源,引发学生知识成长点,让学生在思维碰撞中迸发智慧,在质疑交流中增长才干,从而提高学生的复习效果.

例3 已知函数f(x)＝x3＋ax2＋bx＋3(a、b∈R),若函数f(x)在x＝1处取得极值,且在区间(2,＋∞)上单调递增,求a的取值范围.

设f′(x)＝0的2个实数根为1和x2,由于函数f(x)在区间(2,＋∞)上单调递增,所以x2∈(1,2],f′(1)＝0,解得

针对以上解法,笔者引导学生质疑反思、交流讨论,提出自己的疑问:此题解题过程和结果存在错误,当函数f(x)在x＝1处取得极值时,(1,＋∞)上单调递增也满足题意条件,因此,设f′(x)＝0的2个实数根为1和x2时,也有可能是x2＜1,而不仅仅是x2∈(1,2],于是,经过学生的深入分析和讨论,最终得出上述问题的答案为a≥－9/2,且a≠－3.

总之,在高中数学生成性复习课堂教学中,教师要还学习主动权于学生,以学生为中心、以问题为核心,引导学生分析探究、多向思维、质疑交流,从而提高复习教学效率.

江苏省建湖县高级中学)