浅谈数学试题本质思考的重要性

◇ 江苏 赵一霖

浅谈数学试题本质思考的重要性

◇ 江苏 赵一霖

众所周知,数学问题的解决是数学教学的核心,平时教学中教师对数学问题的研究、编制往往非常重视,从问题的多方面对学生进行训练.笔者也常常遇到这样的情况,类似的错误刚分析完毕,学生又在同样的问题中继续犯错,教师讲得辛苦却效果很差.这是非常值得思考的一个问题,试想若能解决这样的问题,那么解题教学的效率就会大大提高.

数学最重要、最核心的是概念.但是学生对于概念的理解却并未达到我们的目标.比如解析几何中椭圆、双曲线、抛物线的定义,其实很多学生是根本不了解的.

例2 如图1,AB是平面α外固定的斜线段,B为斜足.若点C在平面α内运动,且∠CAB等于直线AB与平面α所成的角,则动点C的轨迹为________.(填“圆、椭圆、双曲线、抛物线”中的一种或几种)

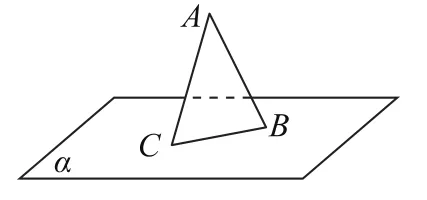
图1

分析 例1考查的是解析几何第一定义,即感官定义,对于能力较差的学生来说,其对于条件的分析往往没有思考问题所需要考查的方向,若能积极思考定义,从定义出发,这样的问题对于能力较弱的学生也能轻而易举地解决.例2从立体几何中去思考解析几何,挖掘了圆锥曲线为何称之为圆锥曲线的原因.问题背后体现的是教材“圆锥曲线”这章中的章头图,用平面截圆锥,若平面平行于圆锥底面,则截口曲线是圆;稍有倾斜,则截口曲线是椭圆;与圆锥母线平行的平面截圆锥,截口曲线是抛物线;截对顶摆放的2个圆锥得到的平面,截口曲线是双曲线.这种问题背后的本质思考,就是数学教学最基本的、也是最重要的东西——概念.笔者以为,很多时候教师仅仅是讲题,并没有讲透问题背后的本质,就题论题式的教学是事倍功半的.

本质思考 例1综合考查了椭圆、双曲线的定义、标准方程和几何性质.由得所以a＋b＝2(a－b),得a＝3b.所以

例2因为∠CAB等于直线AB与平面α所成的角,不妨记为θ,因此动点C在空间的轨迹是圆锥表面上的点.又直线AB与平面α所成的角大小也是θ,而动点C既在圆锥上又在平面α上,则此时的截口曲线是椭圆.

巩固1 F1、F2是椭圆C1:x2/4＋y2＝1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是________.

分析 不妨令BF1＝m,BF2＝n,利用椭圆和双曲线定义可知m＋n＝4,m－n＝2a,进而解得m、n.又∠F1BF2是直角,由勾股定理易得离心率

巩固2 二面角α-l-β大小120°,AB垂直平面β交l于B,动点C满足AC与AB成30°角,则点C在平面α和β上的轨迹分别是________.(填“圆、椭圆、双曲线、抛物线”中的一种或几种)

分析 类似于例2,首先将平面α和β抽去,那么动点C满足AC与AB成30°角的空间轨迹是以AB为轴的圆锥,此时点C在圆锥的母线上,现将平面β与圆锥相截,由条件“AB垂直平面β交l于B”可知截口曲线为圆,再将平面α与圆锥相截,考虑到平面α与轴AB成30°角,而母线与轴AB也成30°角,根据圆锥曲线定义可知,截口曲线为抛物线.

说明:类似的问题有很多,笔者给出巩固问题,从概念的角度对于类似问题的认知有了更深入的理解,有助于数学本质的挖掘.

从近年来新课程立足于数学教学需要加强概念教学的理念出发,笔者认为首先数学教学需要脱离题海训练的模式,要从问题背后去挖掘本质.从例1、2我们不难发现,近年来高考热点问题尊崇了新课程改革的理念,对于普通问题背后都有着最基本的数学概念的考查.其次是思考,圆锥曲线第一定义是教材中最感官的阐述,而用平面截圆锥得到的曲线正是为何将椭圆、双曲线、抛物线和圆称之为圆锥曲线的本质(教材章头图).多数学生对于定义的思考和理解、对于截口曲线的认知都是远远不够的,因此教学中需要追求概念本质的思考才是关键.

江苏南通市天星湖中学)