感悟研读教材 培养几何直观———从人教A 版《必修２》说起

◇ 福建 林贤忠

感悟研读教材 培养几何直观
———从人教A 版《必修２》说起

◇ 福建 林贤忠

《普通高中数学课程标准》指出:“培养和发展学生的空间想像能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力,是高中阶段数学必修系列课程的基本要求”.人教A版《必修2》的主要内容有立体几何初步及解析几何初步,这2部分内容的学习离不开几何直观.几何直观是《必修2》教学中必不可少的有效工具,本文就此进行探讨.

1 教材设计突出了几何直观

过去的《立体几何》教材是按照“平面基本性质—点、直线、平面之间位置关系—空间几何体”的顺序来安排,基本上遵循了从局部到整体的原则.而《普通高中数学课程标准》却是按照空间几何体—直线平面之间位置关系—空间向量与《立体几何(选修)》的顺序来进行,实际上采取了“整体—局部—整体”的布局方式.先从对空间几何体的整体感受入手,再以长方体为载体(包括其他的实物模型、实际例子等)研究空间点、直线、平面的位置关系及有关定理,最后在选修中把立体几何与空间向量结合起来,严格地推理论证平行、垂直等有关问题.

新课标“立体几何”中有着大量的图片,这些图片反映出在实际生活中我们时刻与图形打交道,说明立体几何研究的内容与生活有密切联系,所涉及的问题都来源于生活,研究的结果最终又回到实际生活.立体几何中的问题不是数学家闭门造车造出来的,而是生活中实际模型的反映,这些模型在生活中比比皆是,有利于学生直观感知.

三视图是新课标增加的内容,学习三视图的目的是为了进一步认识空间图形,通过空间几何体与其三视图之间的互相转化,对空间图形形成比较完整的认识,进而培养和发展学生的空间想象能力、几何直观能力,更全面、准确地把握空间几何体的结构特征.

在过去很长一段时间,学生都有种错误的认识,所谓解析几何就是用代数、方程、坐标等解析方法去研究几何问题,既然将几何问题代数化处理了,那么就不必重视解析几何中图形的直观性了.新教材“解析几何初步”试图改变这种认识,我们来看看对倾斜角与斜率的教材(人教A版《必修2》)处理部分:

1)提问:过定点P有一直线束,这些直线有何区别?(通过画图让学生直观感知)

2)把直线放入坐标系,引入直线倾斜角概念;

3)举出生活中实际例子(如坡度,进2升3等)让学生去直观感知倾斜角与倾斜度的关系.

例1 (人教A版课本第93页例6)已知A(5,－1)、B(1,1)、C(2,3),试判断△ABC的形状.

本例如果不画图直观感知,先猜测图形形状的话,那么入手将非常盲目.教材对本例的处理就采用了画图直观感知—猜测结果—逻辑证明3个步骤.

新教材模块2的编排意图很明显,就是想突出几何直观对探究的影响,刻意培养学生的几何直观能力.

2 培养目标突出几何直观

几何的学习基本上有4个阶段,即直观感知—操作确认—思辨论证—度量计算.在以往的教材中往往偏重于后2点,缺乏或不太重视直观性特别是几何直观性教学,陷入凡事都得逻辑证明的误区.使学生无形中陷入了“得意忘形”的境界,忽视甚至排斥几何直观,抛弃了几何的原始来源动机与直观.但是几何直观是一种很重要的科学研究方式,是我们认识的基础,是揭示数学本质的有力工具.

《普通高中数学课程标准》多处使用了“观察”“认识”“画出”“直观感知”“操作确认”等行为动词,适当降低了对推理论证的要求,只要求对有关线面平行、垂直关系的性质定理进行证明,而对相应的判定定理只要求学生直观感知、操作确认,从图形中直接得出结论,不过分追求严密性,很多繁难的定理都不证明,这样安排的目的就是为了培养学生的几何直观能力.

3 如何培养学生几何直观能力

3.1 善假于物

新课标在几何教学中强调实物、模型对几何学习的作用,生活中有着丰富的模型供我们使用.比如长方体模型就是在立体几何教学中经常用到的一个“黄金体”,而我们的教室就是长方体,教学中可以让学生在教室内部仔细观察这个长方体的线、面关系,在某些问题的求解中即可利用长方体的相关性质解题.

例2 已知直线l、m,平面α、β,下列命题正确的是( ).

A l∥β,l⊂α⇒α∥β;

B l∥β,m∥β,l⊂α,m⊂α⇒α∥β;

C l∥m,l⊂α,m⊂β⇒α∥β;

D l∥β,m∥β,l⊂α,m⊂α,l∩m＝M⇒α∥β

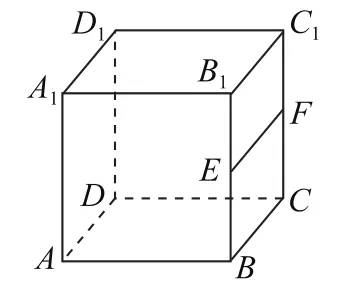
图1

如图1所示,在长方体ABCD-A1B1C1D1中, AB∥CD,则AB∥平面DC1, AB⊂平面AC,但是平面AC与平面DC1不平行,所以A错误;

取BB1的中点E,CC1的中点F,则可证EF∥平面AC,B1C1∥平面AC.EF⊂平面BC1,B1C1⊂平面BC1,但平面AC与平面BC1不平行,故B错误;

可证AD∥B1C1,AD⊂平面AC,B1C1⊂平面BC1,平面AC与平面BC1不平行,所以C错误;

很明显D是面面平行的判定定理,所以D正确.

另外在课堂教学中引入现代信息技术等多媒体手段,在加强几何直观、促进数与形相结合等方面有着特殊的作用.借助多媒体可以形象、直观地帮助学生认识所研究的图形.比如在“解析几何初步”的教学中,运用多媒体可以进一步验证得到的结果,为抽象的认识增添形象的支撑.

例3 (人教A版教材第129页例5)已知线段AB的端点B的坐标是(4,3),端点A在圆(x＋1)2＋y2＝4上运动,求线段AB的中点M的轨迹方程.

本例中在探究点的轨迹时,可以借助信息技术,让学生先感知轨迹的形状,提出猜想,然后再进行准确的论证.

3.2 善于构图

几何图形是空间想象能力的具体反映,同时又为逻辑思维(推理)能力提供几何直观和表象.所以构图是解决几何问题的最基础性的工作.对于条件中没有提示图的几何题,解题时如果学生画的示意图不规范或者不正确,那么这道题就很难解出来.

1)首先要让学生熟练掌握一些基本图形的画法,如几何体的三视图、直线与平面的位置关系(平行与垂直)、空间四边形、三棱锥、三棱柱、球等直观图的画法,并画出这种图形的空间感.

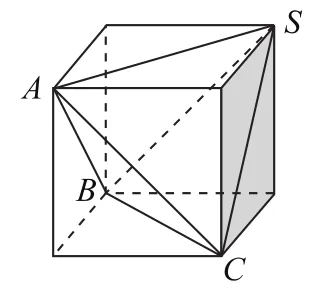
图2

有一些立体几何问题,不通过构造模型是很难作出正确判断的.如:某些几何问题是以正四面体为背景,我们在平面上画一个正四面体时,画出的图形很难将正四面体的性质直观地体现出来,此时如果构造正方体模型,连接正方体的面对角线(如图2所示),即可构造出正四面体,这样正四面体的相关性质得以直观体现.因此在教学中要鼓励学生亲手制作立体几何模型,让学生可以更直接地感受空间几何图形的特征.学生通过亲身体验柱、锥、台的结构特征,逐步形成空间想像能力.

2)对于结构相对比较复杂的几何直观图,要求学生先根据已知的描述进行空间想象,在脑海中形成一个基本图形,大致确定图形的元素之间的位置关系,要分清哪些是可见的轮廓线,哪些是不可见的,最后再画出正式的直观图.

3.3 善于转译

很多数学问题都是用自然文字语言或精炼的数学符号语言来叙述的,这样叙述比较抽象,如果能够转译成形象的图形语言,无疑对解题带来很大帮助.

例如,在学习了一个定义、性质或定理后,我们可训练学生用文字语言、符号语言、图形语言3种语言来表示所学的内容.

例4 线面平行的判定定理的3种表述.

1)文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.

图3

2)符号语言:直线a、b与平面α,若a⊄α、b⊂α且a∥b,则a∥α.

3)图形语言:如图3所示.通过这样的训练不仅提升了学生对概念的认识,也增加了空间想象能力的培养.

再如:教学中在讲解2条直线垂直的判定条件时,在推出结论“如果2条直线l1、l2的斜率k1、k2存在,那么这2条直线垂直的等价条件是k1k2＝－1”后,某些老师就直接教给学生利用结论解题,但是这个结论的几何意义是什么?结论背后有什么本质的东西呢?我们可以利用图形来继续探讨:

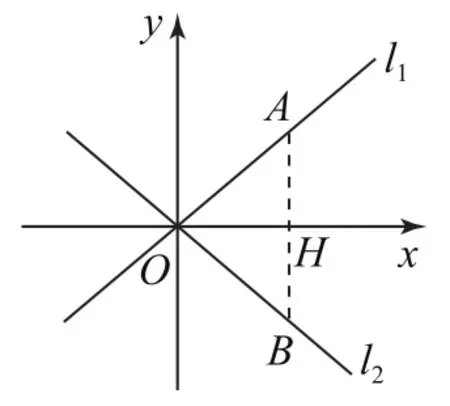
图4

不妨把2条直线平移到坐标原点处如图4.令AB⊥x轴, OH＝1,所以k1＝|HA|,k2＝－|HB|.在Rt△AOB中,因为|OH|2＝|AH|·|HB|,所以k1k2＝－1.

我国拓扑学家张素诚曾说过:对数学中的许多问题来说,“灵魂”往往来自几何.由此可见,几何直观对于激发学生“灵感”的重要性,这就要求我们教师在教学中要尽可能地借助几何直观来分析、讲解问题,这样既能培养学生借助几何直观解决问题的意识,又能为学生创造用几何直观去寻找解题方法的条件.

福建省泉州师范学院附属培文实验高级中学)