灵活处理初中数学教材资源的实践与探究

童敏（四川省叙永县分水中学校）

灵活处理初中数学教材资源的实践与探究

童敏
（四川省叙永县分水中学校）

新课程下的数学教材只是一种育人的手段，只为教师提供一个范例，是一个载体，“新课程改革”倡导教师要成为研究者，教师不仅要解读教材，同时，以教材为中心，适当向外延伸。因此，我们就有必要对新教材进行研究和挖掘，而不是生搬硬套简单地“教教材”。现就如何灵活和创造性地使用教材谈一谈我的做法。

一、根据学生的认知水平，对教材顺序进行适当的调整

根据不同地域、不同学校环境及不同学生的认知水平等情况，可对教材内容的顺序进行适当的调整，有利于提高自己的教学效果。如七年级（上）“3.2—3.3解一元一次方程”这两节，是探究“一元一次方程的解法”。教材给出的首先是实际问题，然后列方程，利用等式的性质归纳出解方程的方法、步骤。由于我校地处贫困边远山区，学生列方程存在很大的困难，正确列方程会占据很多时间，教材对问题的解答也不很规范，无答语且步骤重复。所以我在教学时将这两节内容进行调整，先就一元一次方程的解题步骤，出示几道一元一次方程题（有梯度），要求学生利用等式性质解，然后归纳出方程的解法和步骤，最后解决教材提出的实际问题，这样所花时间会减少且解题规范。这样灵活地调整更符合学生的学习实际，也符合学生的认识规律，有利于学生对知识的探究和掌握，增强学生的成就感和提高学生的学习兴趣。

二、对教材内容进行适当的调整

1.对教材内容进行适当的补充

我们在使用教材的过程中，根据本校实际需要对教材内容进行适当的补充，以便更加符合学生的需求。如学习七年级（上）“1. 4有理数的乘除法”时，可补充“水池中水位升降”或“汽车向东（或向西）行驶”的例子，以帮助学生理解有理数乘法法则。又如学习“勾股定理”给学生补充我国古代数学家赵爽的故事和赵爽弦图以及关于勾股定理的证明，二项式展开式介绍“杨辉三角”等。这样可以丰富课堂内容，提高学生的学习兴趣，激发学生的爱国热情，并体会数学在人类社会发展中的重要作用。

2.对教材中的例题进行适当的修改

在使用教材的过程中，教师可以根据学生实际及认知情况的需要对教材内容进行适当的删改，以便更加符合学生的实际。如七年级（上）第144页的“数学活动”中的“活动1：制作火车车箱的模型”。教材安排这个活动内容对我们贫困山区农村学校的学生来说，有的从来没有见过火车，这样的活动学生操作起来比较困难，而且教材在活动后面的问题“你见过其他形状的火车车箱吗？类似地制作出它们的模型？”学生会更加犯难。由此，我对这个活动的内容进行修改，改用当地学生常见的又符合当地学生实际的“汽车车箱”，这样学生操作起来比较顺利，容易体会到成功的喜悦，激起学生学习的兴趣。

三、对教材习题的教学要灵活多变

教材中的习题在解题思路上具有典型性和代表性，在知识掌握、运用和由知识转化为能力的过程中具有示范性和启发性。使知识相互联系，提高学生对解法的理解和提高解题的技巧。如已知：如图1，点C为线段AB上一点，△ACM、△CBN是等边三角形。求证：AN=BM

图1

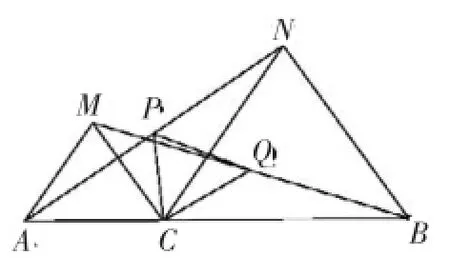
图2

证明：∵△ACM和△CBN是等边三角形

∴MC=AC，CN=CB，∠ACN=∠MCB

∴△ACN≌△MCB

∴AN=BM

变式1：在上题中，连接DE，求证：（1）△DCE是等边三角形（2）DE//AB

分析：（1）可证△ADC≌△MEC，则DC=EC，因为∠DCE=60°，所以△DCE是等边三角形。

（2）由（1）易证∠EDC=∠ACM=60°，所以DE//AB

变式2：上题中，连接CF，求证：CF平分∠AFB

分析：过点C作CG⊥AN于G，CH⊥BM于H，由△ACN≌△MCB，可得到CG=CH，

所以CF平分∠AFB

变式3：如图2，点C为线段AB上一点，△ACM、△CBN是等边三角形，P是AN的中点，Q是BM的中点，求证：△CPQ是等边三角形

证明：∵△ACN≌△MCB

∴AN=BM，∠ABM=∠ANC

又∵P、Q分别是AN、BM的中点

∴△BCQ≌△NCP

∴CQ=CP，∠BCQ=∠NCP

∴∠PCQ=∠NCP+∠NCQ=∠BCQ+∠NCQ=∠NCB=60°

∴△CPQ是等边三角形

数学习题目的在于全面系统地巩固基础知识，进一步提高学生的分析能力和解题能力。

变式2：如图3，已知⊙O的半径为r，C、D是直径AB同侧圆周上的两点，弧AC的度数为96°，弧BD的度数为36°，动点P在AB上，则CP+PD的最小值为________

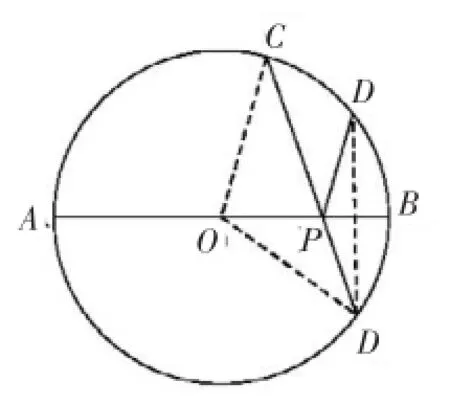
图3

解：如图3，设D′是D关于直径AB的对称点，连接CD′交AB于P，则P点使CP+PD最小。弧CD的度数为180°-96°-36°= 48°，弧CD′的度数为120°，所以∠COD′=120°，从而易求CP+PD′=所以CP+PD的最小值为

本例利用“泵站问题”进行迁移变式，逐步探究了几种常见的图形中两条线段之和最短问题，这样有利于学生解题思想方法的形成、巩固，达到了透彻理解该基本问题的目的。

灵活使用教材，应该是一项长期艰巨的工作。同样的教材会因为学生具体情况不同而出现不同的教学效果，所以我们经常说要树立“用教材教”的新观念，而不是机械地“教教材”，教材的编写也有意识地给老师留下研究和拓展的空间。作为教师，灵活地使用教材，变“死教”教材为“活用”教材，使课堂教学生动而有效。只有在教学中不断地学习教育理论，更新教育观念，大胆探索，积极思考，不断积累、总结经验，才能在教学实践中结合学生实际，更有效地挖掘教材内涵，轻松自如地驾驭教材，提高学生探究学习的能力，实现新课程目标。

陈金红，郭作华.初中数学教材灵活处理点见［J］.湖南教育：下，2014（7）：36.

·编辑谢尾合