从高考题中领悟新课标改革下数学课的变化

崔丽君（大连旅顺三高中）

从高考题中领悟新课标改革下数学课的变化

崔丽君
（大连旅顺三高中）

从课标卷考试说明看高考主要考查七方面能力要求：（1）运算求解能力；（2）空间想象能力；（3）数据处理能力；（4）抽象概括能力；（5）推理论证能力；（6）应用意识；（7）创新意识。

从高考难度看基本题、中档题占75%～80%，选、填题最后一两个，解析几何，导数最后一问难一些。得100分～120分，不需很高水平，新课标高考的数学题难度是稳中有降的，而且更侧重于考查学生的能力。

（2010全国卷Ⅱ理数）19．如图，直三棱柱ABC-A1B1C1中，AC=BC，AA1=AB，D为BB1的中点，E为AB1上的一点，AE=3EB1．

（Ⅰ）证明：DE为异面直线AB1与CD的公垂线；

（2011全国卷Ⅱ理数）（18）如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB= 60°，AB=2AD，PD⊥底面ABCD。

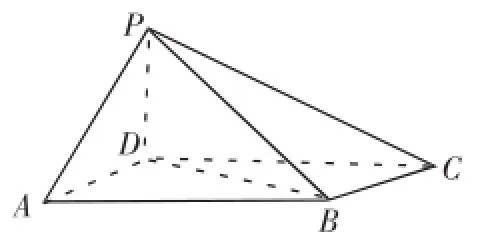
（Ⅰ）证明：PA⊥BD；

（Ⅱ）若PD=AD，求二面角A-PB-C的余弦值。

（2014全国卷Ⅱ理数）18.如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.

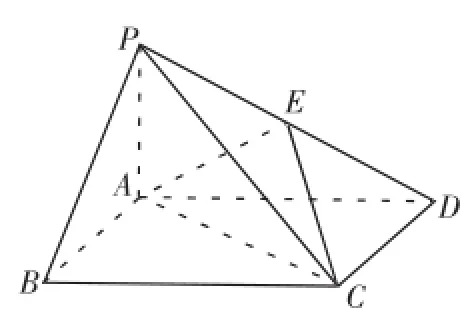
（Ⅰ）证明：PB∥平面AEC；（Ⅱ）设二面角D-AE-C为 60°，AP=1，，求三棱锥

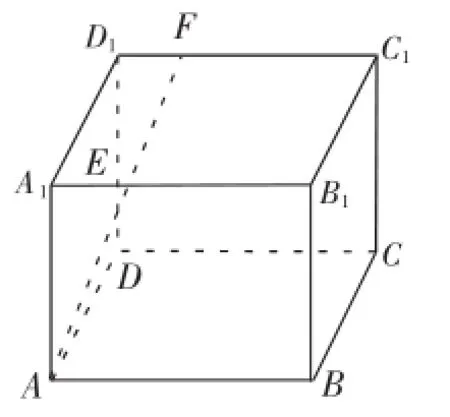
（2015全国卷Ⅱ理数）19．如图，长方体ABCD—A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4，过点E，F的平面α与此长方体的面相交，交线围成一个正方形。

（1）在图中画出这个正方形（不必说明画法和理由）；

（2）求直线AF与平面α所成的角的正弦值。

从2010年到2015立体几何第一问明显看出难度降低，2015全国卷Ⅱ理数19（1）在图中画出这个正方形“不必说明画法和理由”充分考查了学生的空间想象能力。在新课标改革的环境下，课堂教学结构上应更新教育观念，始终坚持以学生为主体，以教师为主导的教学原则。

数学课可改造课本上的例题、习题为“问题解决”的形式（2015全国卷Ⅱ理数）

（17）△ABC中，D是BC上的点，AD平分∠BAC，△ABD是△ADC面积的2倍。

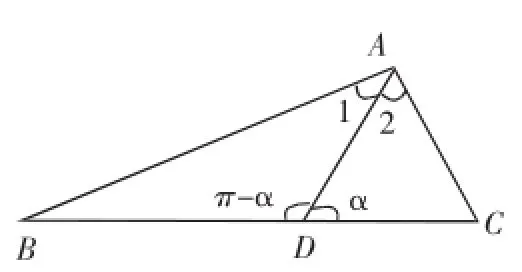
解法分析：这是一个注重运算的范例！

（1）题设“△ABD是△ADC面积的2倍”推出“BD=2DC”；

sin∠B和sin∠C如何表示？在△ABD和△ADC中，由正弦定理模型指出sin∠B=ADsin∠1/BD，sin∠C=ADsin∠2/DC，所以，。

△ABC中，D是BC上的点，AD平分∠BAC，△ABD面积是△ADC面积的2倍。

我们应重视课本上的例题和习题，可以改造课本上一些常规性题目，打破模式化，使学生不仅仅是简单的模仿。比如，把条件、结论完整的题目改造成只给出条件，先猜结论，再进行证明；或给出多个条件，首先需要收集、整理、筛选以后才能求解或证明，打破条件规范的框框；也可以给出结论，让学生探求条件等。在共同的教学情景中，教师的教和学生的学，实际上是一种相互探讨和共同学习、共同解决学习中各种问题的探究活动。引导学生积极参与数学课堂教学的全过程，而不是只让学生参与练习、回答问题等局部过程。这有利于师与生、生与生之间的多向交流，取长补短。有利于使教师、学生的角色处于随时互换的动态变化中，促进学生的创新思维。学生在探索中出现这样或那样的问题错误是难免的，也是允许的。

重要启示：在∠OMN≥45°时，圆上存在符合条件的点，是非逻辑的、直觉的思维！说明课标卷的新理念。在课堂上多给学生一些鼓励，一些支持，让学生建立自信，对学生的正确行为或好的成绩表示赞许，少一些打击和嘲讽，培养学生面对陌生的问题情景，挖掘隐含信息，综合运用数学知识解决问题的能力和心理素质。“好学生是夸出来的”，每个人都渴望得到别人的赏识，学生更是如此。有了自信心学生才能融入课堂进行讨论，良好的数学课堂教学应该是师生之间、学生之间多边活动的有效合作过程。

创新，既需要智力的参与，也离不开情感的支持。教师是保护学生创新能力发展的“监护人”。因此，在数学课堂教学中，要注重对学生创新情感的培养，鼓励学生发扬“打破沙锅问到底”的精神。学生的情感十分丰富，如热爱、美感、羡慕等，这些都可以成为创新的动机。数学课堂教学过程不仅是认知信息的交流，也是情感信息的交流，教学过程需要教师真挚情感的灌注。

王娟萍.用新课程理念构建生活化的数学实效课堂［J］.新西部，2010（10）.

·编辑孙玲娟