浅谈数学教学中的试卷讲评
2016-08-15郑彩琴福建省漳州市第九中学
郑彩琴(福建省漳州市第九中学)
浅谈数学教学中的试卷讲评
郑彩琴
(福建省漳州市第九中学)
在平时教学中,大多数教师尤其是青年教师认为试卷讲评就是对对答案,再根据自己的理解,把试卷逐题讲评一遍。学生处于被动接受的境地,深层自主思考能力被埋没,教师还一直抱怨学生不用心,认识问题不求其解,考过的题型仍不会,总是一错再错,把讲评课变成批评课,前述问题的症结在于教师所采用的讲评方法上。
试卷讲评;数学教学;讲评方法
试卷讲评是教学活动的一个组成部分,是阶段学习的终点,也是链接新知识的起点,更是探究学法、培养创新能力的桥梁,同其他教学环节一样,承担着培养学生自主探索和自我评价能力、独立性、创造性思维品质的重任。如何上好试卷讲评课,提高讲评质量,笔者认为应该做好以下几个方面:
一、正确认识试卷讲评课的重要性
不论是教师还是学生,都应该清楚地认识到:试卷讲评课起着进一步巩固知识,理解概念,弥补缺漏,纠正错误,揭示规律,提高解题能力及拓展思维的重要作用。教师首先要认真阅卷,亲手批改,掌握第一手材料,帮助学生提高认识,鼓励学生提问、概括、假设和陈述,调动学生上课的主动性,形成有积极创意的课堂氛围。
二、做好试卷分析统计工作
一张精心设计的试卷,不论是单元卷还是综合卷,教师都应该认真评改,然后进行试卷分析,统计正确答案、不正确答案、不全面答案,没有回答及独特见解答案的人数,详细记录“病情”,找出“病源”,为上好试卷讲评课做好课前准备。
三、教给学生科学有效的订正方法
留意平时的考试就会发现,对于某些试题,多次考查也多次讲评后再考查,学生还是存在错答或不会解答的现象,学生常说“许多题目似曾相识,但百思不得其解”,究其原因主要是学生在试卷讲评课上只习惯于将错误的答案改为正确的就了事。因此,讲评课上要教给学生科学的订正方法:一要用不同于考试的色笔订正;二要准备错题订正本,将自己的错误解法与正确解法并列抄录,找出病因及医治方法;三要用简单扼要且醒目的字眼在错处注明对错误的原因。如:单位要统一;审题要准、全等,把纯粹“纠错”变为“究错”。这样,在今后的复习中翻阅就会省时、高效,避免重蹈覆辙。
四、引导学生明确试题考查的目的及知识点
讲评试卷,切忌就题解题,应引导学生明确每一道试题考查的目的及知识点。例如,已知方程的解为非负数,求a的取值范围。该题考查的知识点有方程的解的定义、方程的解法、非负数的式子表示及不等式的解法,讲评时,教师要引导学生归纳出这类题的解题思路,以点带面,使讲评达到进一步复习知识及运用知识解题的作用。
五、恰当运用试卷讲评的方法
在平时教学中,大多数教师尤其是青年教师认为试卷讲评就是对对答案,再根据自己的理解,把试卷逐题讲评一遍,学生处于被动接受的境地,深层自主思考能力被埋没,教师还一直抱怨学生不用心,认识问题不求其解,考过的题型仍不会,总是一错再错,把讲评课变成批评课,前述问题的症结在于教师所采用的讲评方法上。因此,为提高讲评质量,可采用以下几种方法:
1.教师设疑,指定学生介入求是的诊断性讲评
教师在批改试卷的过程中,可以了解并选择合适的学生讲解试题。具体做法是:难题请做对的学生谈怎样入手,在哪儿受阻,如何拨开荆棘寻求突破,易错题由做错的学生讲错在哪里,为什么错,如何避免,选择、填空题请做得快而准的学生介绍如何既准又快地收集、处理信息。
2.板书错例,要求学生究根溯源的解剖性讲评
教师先把典型错例写在黑板上,如:3x+3y=6xy,7x-5x=2x2,16y2-7y2=9等,尽可能让学生自己发现错误,弄清产生错误的原因,再从正错的比较中纠正错误,从中提高学生观察、分析、比较、判断等能力。
3.收集不同解法,引导学生考后再思考的发散性讲评
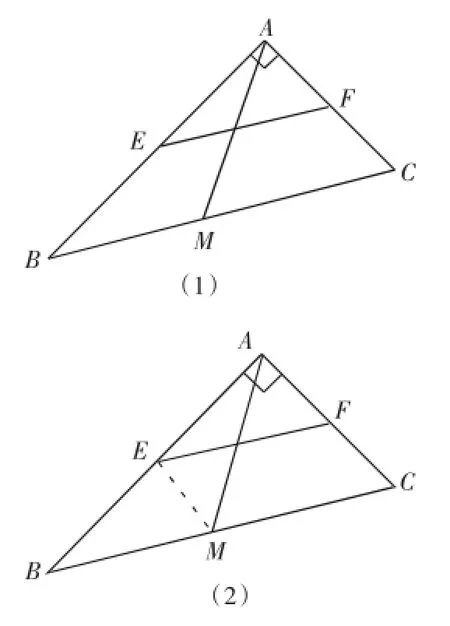
发现问题和解决问题是科学研究的起点。教师在改卷时要注意收集各种不同的解法,并加以对比研究,在讲评课中应舍得花时间介绍各种解法。如一道试题:如图(1):在△ABC中,∠A= 90°,M、F、E分别为BC、CA、AB的中点,求证:EF=AM。大部分学生的BM解法是:由E、F分别是AB、AC的中点得(1),又∠A=90°,M为BC中点得,从而证得EF=AM。以“第三条线段”为媒介,是证明线段相等的基本的、常用的方法。在讲评中不仅要肯定学生的这种常规解法,还要引导学生作多角度的思考。如证法(2)构造全等三角AF形,如图(2),连结EM,由E、M分别为EC、AB、BC的中点得,EM∥AC。由∠A=90°得∠MEA=∠FAE=90°,显然Rt△MEA≌Rt△FAE,可得EF=AM。又如证法(3),构造平行四边形,把一条线段“推”到恰当处,与另一条线段构成等腰三角形。过程是:如图(2),连结EM,由E、M分别是AB、BC中点得EM=AC,EM∥AC,又F为AC中点,可得EM= FC,EM∥FC,得四边形EMCF为平行四边形,有EF=MC,由∠A= 90°,M为BC中点可知,从而证得EF=AM。如此“借题发挥”,鼓励解法新颖思路简捷的学生,多角度、全方位地分析问题,以点带面复习,巩固所学知识,就会收到较好的讲评效果。
4.注重内涵,提示学生寻根究底的探索性讲评
一般地,一份试卷中,班级有一半左右学生出错或普遍答不出来的试题,教师应详细分析,给学生必要的思考时间,适时进行有效的提示,鼓励学生探索,大胆猜想、比较、验证等积极的智力活动,在求解过程中发现规律,活化相关知识,教给学生探索问题的方法,提高解题能力。
5.开拓外延,巩固讲评效果的延伸性讲评
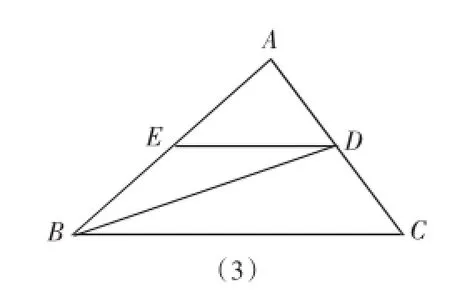
遵循巩固性原则,针对讲评所涉及内容及试卷反馈信息,教师要根据学生的不同程度再设计好巩固作业题,把重点放在题目的延伸上。可以设计些能用多种知识处理同一问题的一题多解型题目,也可以设计些把试题中的题目条件、结论作些改动的变式题。如图(3),已知△ABC中,∠ABC的平分线交AC于D,DE∥BC交AB于E,求证:EB=ED。
讲评时引导学生观察分析这道题的证明,从中发现这道题的实质,由此可以布置以下变式题:
(1)如图(4),△ABC中,∠ABC、∠ACB的平分线交于O,过点O作DE∥BC交AB于D,交AC于E,求证DE=BD+CE。
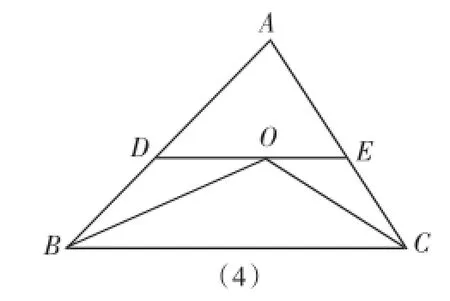
(2)如图(5),△ABC中,过A作BC的平行线,分别交∠B、∠C的外角平分线于D、E,求证:DE=AB+AC。
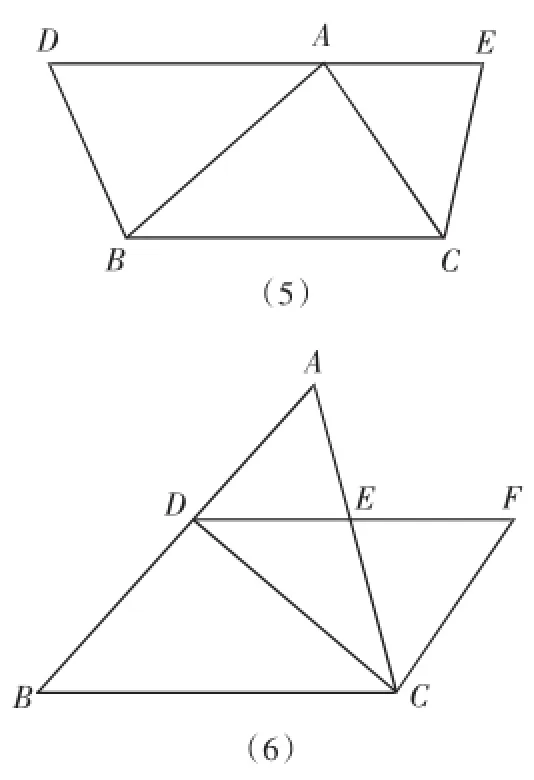
(3)如图(6),已知△ABC中,∠C的平分线交AB于D,过D 作BC的平行线交AC于E,交∠C的外角平分线于F,求证:DE= EF。
通过这样的延伸,从另一角度再现试卷中的薄弱点,有利于学生对知识的归类,深化理解所学知识,使学生顺利地完成讲评,为自己解题能力的提高,不再旧病复发而感到自我成功的喜悦,大大调动了学习的积极性。
综上所述,试卷讲评课中,教师讲前认真分析试卷,讲时启发考后再思考,通过知识组合优化,把问题逐步引申,拓展,使学生动脑、动手探索规律,将使每次考试都有较大的收获,达到新的起点。
张利华.漫谈试卷讲评的四种方法[M].数理化解题研究,2006(8).
·编辑丁可楣
