基于自组织映射神经网络的蛋白质序列分析模型❋

刘珑龙， 马　蒙， 刘毛娟

(中国海洋大学数学科学学院， 山东 青岛 266100)



基于自组织映射神经网络的蛋白质序列分析模型❋

刘珑龙， 马蒙， 刘毛娟

(中国海洋大学数学科学学院， 山东 青岛 266100)

摘要：为了对蛋白质序列进行更精确合理地相似性分析，本文将氨基酸的排列方式与其理化性质相结合，提出了一种基于自组织映射神经网络的聚类模型。首先，采用Wang和Wang的方法把蛋白质序列转化为一条5-字母序列，并将5个字母均匀分布在以原点为圆心的单位圆周上，得到蛋白质序列的位置坐标x，y。然后，结合氨基酸的3个理化指标，进而用一个5-维向量来表示一个氨基酸。最后，运用自组织映射神经网络对不同的蛋白质向量进行聚类分析。本文最后的数值试验部分对9个不同物种的线粒体NADH脱氢酸的蛋白质序列进行了相似性分析，实验结果在一定程度上验证了模型的有效性。

关键词：蛋白质序列； 理化指标； 自组织映射神经网络； 相似性分析

引用格式：刘珑龙，马蒙，刘毛娟.基于自组织映射神经网络的蛋白质序列分析模型[J].中国海洋大学学报(自然科学版), 2016, 46(7):130-135.

LIU Long-Long, MA Meng, LIU Mao-Juan. A model of protein sequences based on SOM neural network[J].Periodical of Ocean University of China, 2016, 46(7):130-135.

随着生物分子数据的迅速增长，对这些数据进行分析得到对人类有用的信息变得越来越重要。尽管DNA序列的图形表示已经被广泛地研究，但是对蛋白质序列的图形表示研究只是近几年的事[1-4]。主要原因是蛋白质序列中氨基酸种类数目远远大于DNA序列中碱基的种类数目(20∶4)。在DNA序列中，4种碱基最多只有4！=24种不同的排列顺序。如果把DNA序列的这些表示方法直接推广到蛋白质序列，则将会有20！种可能的方式，这个数字是难以接受的。这也是蛋白质序列图形表示方法比较少的一个主要原因[4,16]。此外，大多数蛋白质的图形表示存在一定程度的任意性，如将氨基酸对图形顶点进行分配等[10-12]。

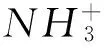
1　网络模型

1.1 蛋白质序列的矩阵表示

从数学角度来说，一个蛋白质序列可以被看做是在20种氨基酸的字母表Ω上的字符串，即Ω= { A，C，D，E，F，G，H，I，K，L，M，N，P，Q，R，S，T，V，W，Y}。根据氨基酸的物理化学性质以及它们之间的相互作用，Wang 和Wang[7]把20种氨基酸分成下面5类: { C，M，F，I，L，V，W，Y} ，{ A，T，H} ，{ G，P} ，{ D，E} 和{ S，N，Q，R，K}。分别取每类中的一种氨基酸I，A，G，E 和K 作为的代表，这样，一条蛋白质序列可以被简化成一条五字母序列的蛋白质序列。例如，Randic[4]文章中的yeast saccharomyces cerevisiae的蛋白质序列为WTFESRNDPAKDPVILWLNGGPGCSSLTGL，其对应的5-字母序列片段为：IAIEKKKEGAKEGIIIIIKGGGGIKKIAGI。Jeffrey将A, C, G, T4个碱基分布在正方形的4个顶点上,最终得到DNA序列对应的图形[9]。受此启发，对于任意一条5-字母序列, 我们将5个字母均匀分布在以原点为圆心的单位圆周上, 并赋予它们坐标:xi0=cos(2iπ/5), yi0=sin(2iπ/5) 其中i=0,1…,4。

设S=S1,S2,…,Sn是一条5-字母序列, 类似于Jeffrey的方法, 我们定义同态δ:δ(S)=δ(S1)δ(S2)…δ(Sn)将S映射到平面上的n个点P1,P2,…Pn。其中δ(Sk)=Pk=(xk,yk)由下述公式得到：

(xk,yk)=

(1)

规定x0=0,y0=0。这样我们就得到了一个表示氨基酸的5维向量的前2个元素x，y。

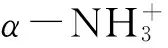
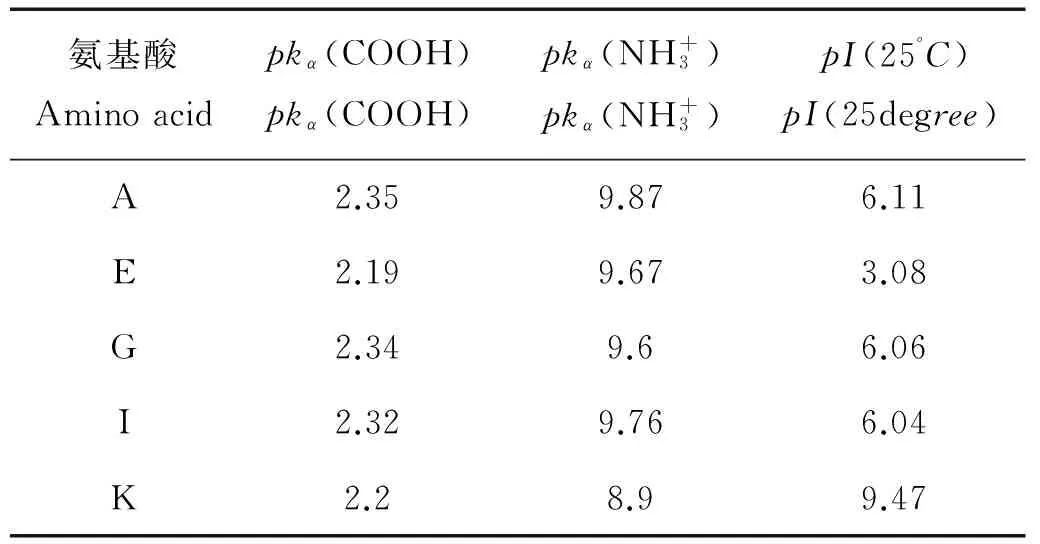
表1　5个氨基酸的3个理化性质

1.2 数值刻画——中心坐标法

(2)若xmin=xmax, 则x′=xmin。

1.3 SOM神经网络

采用有导师学习规则的神经网络要求对所学习的样本给出“正确答案”，以便根据误差的大小改进自身的权值，提高正确解决问题的能力。然而在很多情况下，人在认知过程中没有预知的正确模式。对于这种学习方式，基于有导师学习策略的神经网络是无能无力的。自组织神经网络的无导师学习方式更类似于人类大脑中生物神经网络的学习，能够对外界未知环境进行学习或模拟并对自身的网络结构进行调整，实现对输入模式的自动分类。

1.3.1 SOM神经网络的结构自组织映射(SOM)神经网络是自组织神经网络的一种，是由荷兰学者Teuvo Kohonen于1981年提出的。常用的SOM神经网络模型由输入层和输出层组成；输入层各神经元通过权值向量将外界信息汇集到输出层的各神经元。输出层节点与输入层节点为全连接，输入层、输出层内部节点之间没有连接关系。输出层内的每个神经元与其邻域连接，此链接是相互激励的关系，训练后输出层不同节点代表不同的分类模式。输入层神经元的数量由分类衡量指标的个数决定。输出层可以由一维或二维网络矩阵方式组成。SOM神经网络拓扑结构如图1所示。

图1　 SOM神经网络拓扑结构

图1中，网络上层有m×n=M个输出神经元，按二维形式排列成一个矩阵；输入神经元位于下层，有K个矢量，即K个神经元，并且所有输入神经元到所有输出神经元之间都有权值连接。

SOM神经网络以无导师教学的方式进行网络训练，网络通过自身训练，自动对输入模式进行分类。

1.3.2 SOM神经网络的学习SOM神经网络学习算法包含竞争、合作和更新3个过程。

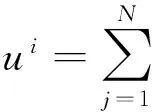
Ⅱ.在合作过程中，确定获胜神经元的加强中心。拓扑邻域的中心就是在竞争过程中得到的获胜神经元，在邻域范围内的神经元称为兴奋神经元，即加强中心。

Ⅲ.在更新过程中，采用Hebb学习规则的改变形式，对网络上获胜神经元拓扑邻域内的神经元进行权值向量的更新。

SOM学习算法的具体步骤如下：

1.网络初始化

用随机数设定输入层和输出层之间权值的初始值。

2.输入向量

把输入向量X=(x1,x2,…，xN)T输入给网络的输入层。

3.计算输出层的权值向量和输入向量的距离

这里，输出层的第j个神经元和输入向量的距离，按下式给出：

(2)

式中ωij：输入层的i神经元和输出层的j神经元之间的连接权值。

4.选择与权值向量的距离最小的神经元

计算并选择使输入向量和权值向量的距离最小的神经元，如dj为最小，将其称为胜出神经元，记为j*，并给出其邻接神经元集合。

5.权值的学习

胜出神经元和其邻接神经元的权值，按下式更新：

Δωij=ηh(j,j*)(xi-ωij)

式中η：一个大于0小于1的常数；h(j,j*)：邻域函数，用下式表示：

(3)

式中σ2随着学习的进行而减小。因此，h(j,j*)的范围，学习初期很宽，随着学习的进行而变窄。也就是说，随着学习的进行从粗调整向微调整变化。这样，邻域函数h(j,j*)可以起到产生有效映射的作用。

6.是否达到预先设定的要求

如达到要求则算法结束；否则，返回到步骤2，进入下一轮学习。

在SOM中，由式(3)可见，胜出神经元和其附近的神经元全部接近当时的输入向量。学习初期，根据邻域函数h(j,j*)，在附近有很多神经元，形成粗略的映射。随着学习的进行，h(j,j*)变窄，胜出神经元附近的神经元数变少，因此，接着继续进行局部微调整，空间分辨调高。

2　数值实验

在本节，首先取9个不同物种的线粒体NADH脱氢酸的蛋白质序列按2.1,2.2进行预处理，得到描述一种蛋白质序列的5维向量L，然后输入到SOM神经网络进行分类，最后进行相似性分析。

2.1 数据来源

以9个不同物种的线粒体NADH脱氢酸为例说明上述模型的有效性。9个不同物种的线粒体NADH脱氢酶相关信息见表2。

表2　9个不同物种的线粒体NADH脱氢酶信息

根据表2提供的序列代码，从NCBI上下载这9个不同物种的线粒体NADH脱氢酶的蛋白质序列。

2.2 9个不同物种的线粒体NADH脱氢酶的蛋白质序列的矩阵表示

现以Human的一段蛋白质序列为例，说明蛋白质序列的向量表示方法。Human的一段长度为10的蛋白质序列:mtmhttmttl对应的五字母序列片段为:iaiaaaiaai，运用公式(1)并结合各理化指标得到相应的向量表示，进而得到一个10×5的矩阵：

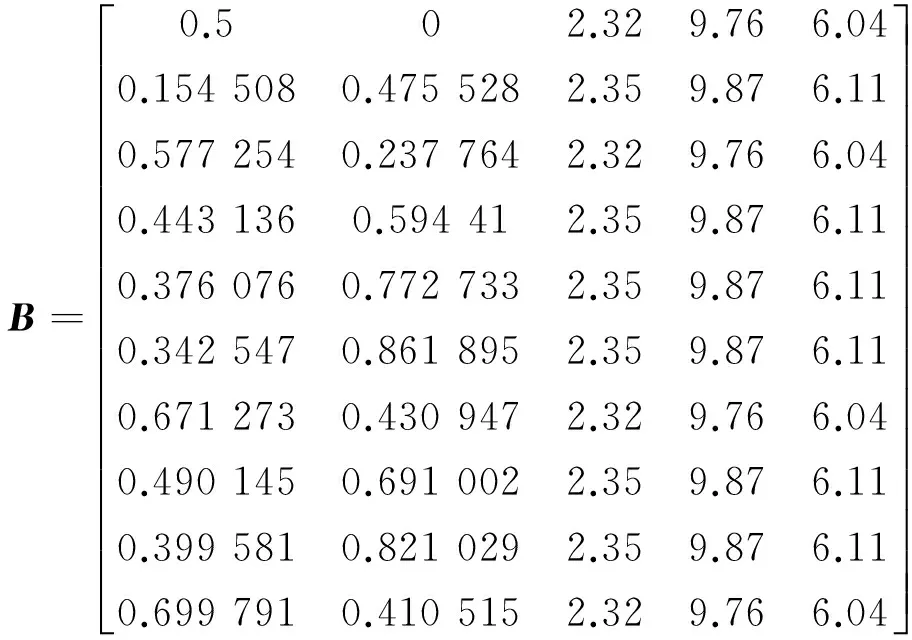
2.3 获取9个不同物种的线粒体NADH脱氢酶的蛋白质序列的中心坐标

为避免数值的大小对实验的影响，对矩阵B的每列进行归一化，得到最终的矩阵：

P=

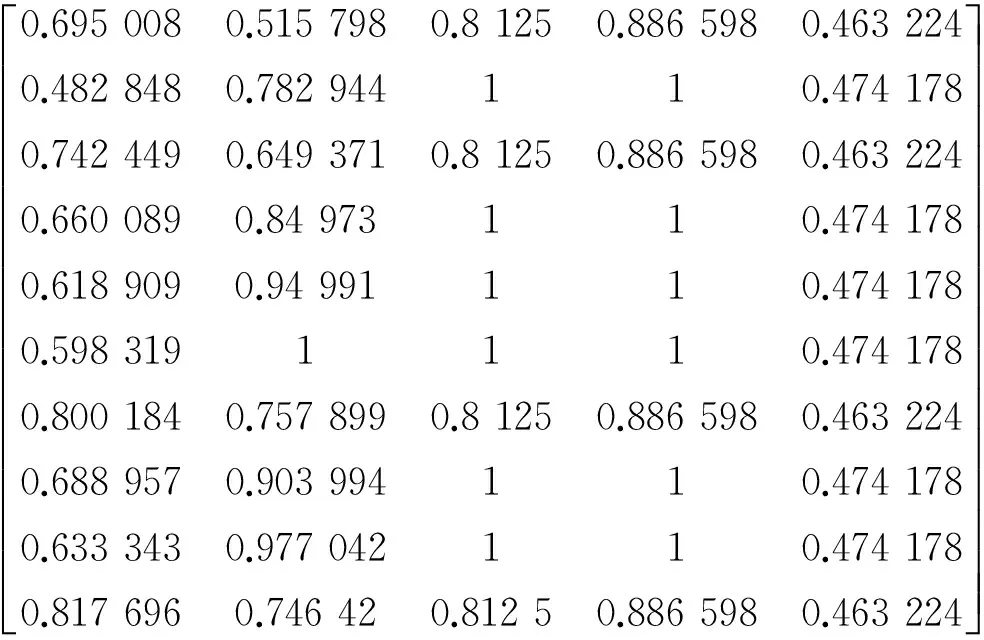
若对整个Human的蛋白质序列进行上述步骤，将会得到一个603×5的矩阵。对该矩阵运用中心坐标法得到一个5维的向量L=(0.6785,0.5291,0.6729,0.6982,0.567)′。

对其他8个不同物种的线粒体NADH脱氢酶的蛋白质序列也做同样的处理。

2.4 建立SOM神经网络

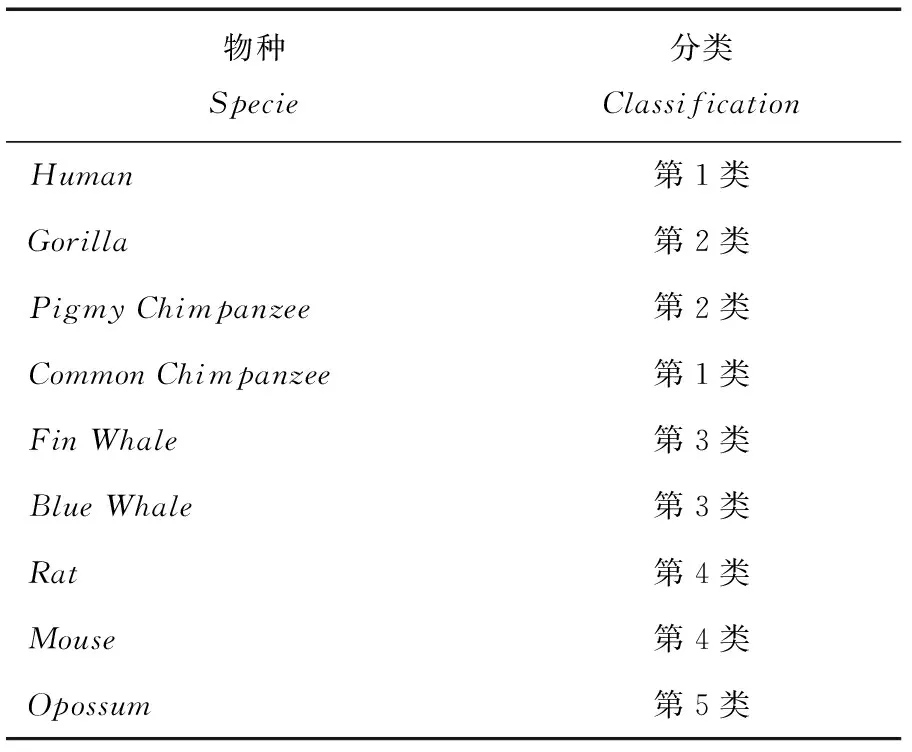
表3　9个物种的线粒体NADH脱氢酶的分类结果表

2.5 网络模型的比较

本节与FenglanBai和TianmingWang在OnGraphicalandNumericalRepresentationofProteinSequences文章中提出的方法进行对比。FenglanBai和TianmingWang首先把20个氨基酸放入正12面体上，在笛卡尔坐标系下表示每个氨基酸的坐标，进而运用不变量方法得到一个对称矩阵。再次求该矩阵前10大特征值，并将其作为一个10维的向量，利用欧氏距离对这10维向量进行比较，最终得到9个不同物种的线粒体NADH脱氢酶的蛋白质序列的相似性结果。表4显示了9个物种的ND5 蛋白质序列的10 维向量间的欧氏距离。其中H、G、P-C、C-C、F-W、B-W、R、M、O分别代表Human、Gorilla、PigmyChimpanzee、CommonChimpanzee、FinWhale、BlueWhale、Rat、Mouse、Opossum这9中不同的物种。

表4　9个物种的ND5 蛋白质序列的10 维向量间的欧氏距离

从表4中可以看出Human-Gorilla，Human-PigmyChimpanzee，Human-CommonChimpanzee，FinWhale-BlueWhale对应的欧氏距离值较小，表明它们之间的相似性较大。而有些数值与生物学的实际情况不大相符。例如Rat-BlueWhale，Mouse-FinWhale，Opossum-Gorilla之间的数值较小，这个结果与文献[3]中的结果不相符合。而本文提出的方法对这9个物种的ND5 蛋白质序列进行了准确的分类，结果与已知的进化事实一致[13-14]。

3　结语

本文提出了一种对蛋白质进行有效分类的模型，所提出的方法是更为直观简单、方便、快捷。结合氨基酸的中心坐标法及其3个理化指标，文章给出了蛋白质序列的5维向量表示，进而建立SOM神经网络对蛋白质序列进行相似性分析。数值试验部分运用新模型对9个物种的线粒体NADH脱氢酶进行了正确合理的分类。当然，在由蛋白质序列转化为5-字母序列的过程中, 可能会有一定信息的丢失。但也正是这种转化, 才使得将DNA序列的图形表示推广到蛋白质序列成为可能。

参考文献：

[1]Randic M, Zupan J, Balaban A T. Unique graphical representation of protein sequences based on nucleotide triplet codons [J]. Chemical Physics Letters, 2004, 397(1): 247-252.

[2]Randic M. 2-D graphical representation of proteins based on physic-chemical properties of amino acids [J]. Chemical Physics Letters, 2007, 440(10): 291-295.

[3]Yao Y H, Dai Q, Li C, et al. Analysis of similarity/ dissimilarity of protein sequences [J]. Proteins, 2008, 73(4): 864-871.

[4]Randic M, Butina D, Zupan J. Novel 2-D graphical representation of proteins [J]. Chemical Physics Letters, 2006, 419 (26): 528-532.

[5]E Hamori, J Ruskin, H curves. A novel method of representation of nucleotide series especially suited for long DNA sequences [J].J Biol Chem, 1983, 258(2): 1318.

[6]Bai F, Wang T. On graphical and numerical representation of protein in sequences [J]. Journal of Biomolecular Structure and Dynamics, 2006, 23(5): 537-546.

[7]Wang J, Wang W. A computational approach to simplifying the protein folding problem [J]. Nat Struct Biol, 1999, 6(11): 1033- 1038.

[8]Wang J, Wang W. Modeling study on the validity of a possibly simplified representation of proteins [J]. Physical Review E, 2000, 61(6): 6981-6986.

[9]Jeffrey H J. Chaos game representation of gene structure [J]. Nucleic Acids Research, 1990, 18(8): 2163-2170.

[10]Ping-an He, Jinzhou Wei, Yuhua Yao, et al. A novel graphical representation of proteins and its application [J]. Statistical Mechanics and its Applications, 2012, 391(1): 93-99.

[11]Tingting Ma, Yuxin Liu, Qi Dai, et al. A graphical representation of protein based on a novel iterated function system[J]. Statistical Mechanics and its Applications, 2014, 403(1): 21-28.

[12]Ping-an He, Dan Li, Yanping Zhang, et al.A 3D graphical representation of protein sequences based on the Gray code [J]. Theoretical Biology, 2012, 304(7): 81-87.

[13]Pavel Duda, Jan Zrzavy.Evolution of life history and behavior in Hominidae: Towards phylogenetic reconstruction of the chimpanzee-human last common ancestor [J]. Human Evolution, 2013, 65(8): 424-446.

[14]Berger W H.Cenozoic cooling, Antarctic nutrient pump, and the evolution of whales [J].Deep-Sea Research, 2007,54(1): 2399-2421.

[15]Jia Wen, YuYan Zhang. A 2D graphical representation of protein sequence and its numerical characterization [J]. Chemical Physics Letters, 2009, 476(4-6): 281-286.

[16]He Xiao-Mei, Qin Zheng, Chen Jun, et al. New method expression of protein sequence and its application for protein sub-cellular localization prediction [J]. Computational and Theoretical Nanoscience, 2014, 11(3): 873-877.

责任编辑陈呈超

基金项目：❋ 国家自然科学基金项目(61303145)；中央高校基本科研业务经费项目(201362031)资助

收稿日期：2014-07-07；

修订日期：2015-05-20

作者简介：刘珑龙(1966-)，女，副教授。E-mail: liulonglong98@hotmail.com

中图法分类号：Q51

文献标志码：A

文章编号：1672-5174(2016)07-130-06

DOI:10.16441/j.cnki.hdxb.20140227

A Model of Protein Sequences Based on SOM Neural Network

LIU Long-Long, MA Meng, LIU Mao-Juan

(School of Mathematical Sciences, Ocean University of China, Qingdao 266100，China)

Abstract:Combined the arrangement of amino acid with its physicochemical properties, we propose a new clustering model based on SOM neural network in the article, which is more accurate and reasonable to similarity analysis on protein sequences. First of all, the protein sequence is stransform into an 5- letter sequence using the method of Wang and Wang. The 5 letters are uniformly distributed in the unit circle centered on the origin, and then we can get two position coordinates of protein sequences x,y. Next, combined with 3 physicochemical indexes of amino acid, a 5- dimensional vector will be got to represent an amino aci. Finally,using SOM neural network to do cluster analysis of different protein vectors. At the end of this paper, numerical test is carry out to similarity analysis of mitochondrial NADH dehydrogenase from 9 different protein sequences. And the experimental results verify validity of the model in a certain extent.

Key words:Protein sequence； physicochemical properties； SOM neural network；similarity analysis

Supported by the National Natural Science Foundation of China(61303145)；and the Fundemental Research Funds for Central Universities(201362031)