斜向水流作用下海底管线周围水动力特性数值研究❋
2016-08-13常留红蒋昌波程永舟
常留红, 蒋昌波, 程永舟
(1.长沙理工大学水利工程学院,湖南 长沙 410004; 2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410004)
斜向水流作用下海底管线周围水动力特性数值研究❋
常留红1,2, 蒋昌波1,2, 程永舟1,2
(1.长沙理工大学水利工程学院,湖南 长沙 410004; 2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410004)
摘要:管线附近的水动力因素是底床局部冲刷形成的主要原因。基于开源程序OpenFOAM和分离涡紊流模拟方法建立三维数值水槽,数值模型的计算结果与同条件的物理实验结果基本一致。在此基础上,对水流作用角为30°、45°、60°和90°及间隙比为0、0.1、0.3、0.5水流作用下,管线周围的流场结构进行分析,探讨水流作用角和间隙比对管线附近三维水流结构的影响规律。结果表明:随着作用角的增大,管前涡流范围逐步缩小至管线附近,管后涡流范围逐步向下游延伸,且管后涡漩尺度、回流范围与尾涡紊动区域逐步增加,尾涡中心逐步远离管线,且轴向水流逐渐减弱;管后尾涡的产生、脱落,涡旋尺度大小受管线与底床间隙比e/D的影响明显, e/D=0时管线后尾涡的脱落形态不明显; e/D>0.3时,类似圆柱扰流,管后尾涡形态变化不明显。
关键词:海底管线; 斜向水流; 水动力特性; 作用角; 间隙比
引用格式:常留红, 蒋昌波, 程永舟. 斜向水流作用下海底管线周围水动力特性数值研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(7): 105-110.
CHANG Liu-Hong, JIANG Chang-Bo, CHENGYong-Zhou. Experimental study on the hydrodynamics around marine pipelines under oblique flows[J].Periodical of Ocean University of China, 2016, 46(7):105-110.
海洋环境复杂多变,管线失效事故时有发生,直接威胁经济发展和海洋生态安全。调查结果表明[1],海床运动和波、流冲刷是海底管线失效的主要原因之一。国内外不少学者对海流作用下管线冲刷机理进行了大量的研究, Mao[2],Sumer[3],Moncada[4],Yang[5-6]等大量研究认为,管线周围的水流结构及其水动力特性是造成海床冲刷的重要因素。因此,探索水流作用下海底管线附近周围水动力特性和局部冲刷机理具有重要的科学意义和工程应用价值。
国内外相关学者对管线附近的水流结构的数值研究开展了广泛的探讨。纵观以往的数值研究,主要可分为四类:一是基于势流理论的数学模型,模拟水流作用下海底管线的底部冲刷,如Li[7],但由于势流模型不能模拟出管线后方形成的尾涡,因而对管线周围水动力特性模拟尚不够准确;第二种是基于k-ε和k-ω模型发展起来的数值方法,如Brørs[8]、Liang[9]、Ong[10];第三种则是利用大涡模拟(LES)方法对海底管线冲刷进行模拟,Li和Cheng[11];第四种则是利用有限差分和VOF法模拟波浪作用下管线水动力变化规律。研究成果大多采用LES或k-ω模型,能模拟管后出现的大尺度尾涡的产生与脱落。实际海洋环境中作用于管线的水流方向复杂多变,管线附近水流结构三维特征明显。当水流方向与管线斜交时,在管线前后沿管轴向产生较小涡旋,而LES模型为网格滤波的紊流模型,虽能够有效捕捉到管线附近水体内部较大的涡动结构,但对于管线前后表面位置较小的涡动结构,由于小于网格尺度而被模型过滤掉,因而,LES不能有效模拟管线表面前后的流场结构。考虑到RANS模型和LES模型优缺点,Speziale[12]和Spalart[13]等提出了混合RANS/LES方法,目前广泛应用的是分离涡方法(Detached Eddy Simulation, DES)即在流动分离区域,采用LES中的亚格子应力尺度模型模拟;而在壁面的边界层区域,采用RANS模型进行模拟,从而结合了RANS在壁面边界层的优势和LES模拟剪切层和分离流动的优点。
因此,本文采用高精度、并行计算稳定且求解方法先进的开源程序包OpenFOAM,建立三维数值水槽,采用分离涡方法进行紊流模拟,通过分析管线周围三维流线和水平及竖直平面水流结构的变化,研究不同水流作用角和间隙比对管线附近水动力特性的影响规律。
1 数值模型
1.1 控制方程
1.1.1 Navier-Stokes方程在笛卡尔坐标体系中,不可压缩流体的连续方程,通过质量守恒定律和根据动量守恒定律,可推导出连续性方程:
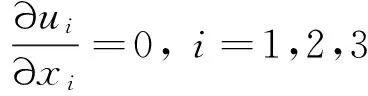
(1)
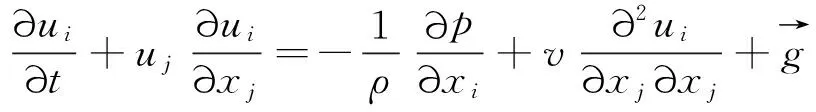
(2)
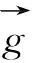
1.1.2 VOF输运方程Berberovi 'c E对经典VOF方法中的体积分数输运方程进行了修正,增加了人工压缩项,使其对自由液面的捕捉更加精确,避免了界面模糊:

(3)
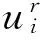
1.2 Spalart-Allmaras DDES
早期DES模型中,由于边界层中LES区域过早地过渡到RANS区域,存在湍动应力损失问题。Spalart[14]修正后的DES版本,即延迟分离涡模型(Delayed Detached Eddy Simulation,简称DDES)。此函数为模型长度尺度与壁面距离的比值。在DDES模型,函数r改写为[15]:
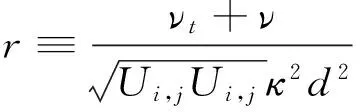
(4)
在对数层r=1,而在靠近边界层边缘逐渐变为0,式(4)分子中ν的存在保证在壁面区域r不为0。并引入了一个新的函数fd,
fd=1-tanh([8rd]3)。
(5)
根据修正后的r和fd,DDES模型重新定义了长度判断函数:
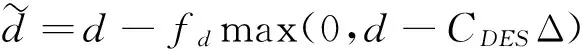
(6)
修正后,特征长度的转换不仅与网格尺度有关,还与涡粘系数的有关。
通过对函数r修改和引入函数fd,保证了DES方法在边界层以内(根据fd判断)区域保持为RANS模型,延迟了DES模型由RANS方法过早的转换为LES方法,避免应力损失。
1.3 数值求解方法
采用有限体积法离散控制方程,保证单元体质量和动量守恒。控制方程中拉普拉斯项采用线性差值计算,梯度项采用高斯线性格式,瞬时项采用逆风差分格式,对流项采用迎风格式。控制方程求解采用压力和速度联合解耦实现,采用PISO算法和SIMPLE算法基础上优化的PIMPLE算法。
1.4 数值水槽
为节省计算资源,数值计算区域仅模拟了部分长度的实验水槽,管线在水流方向上的投影长度为1.4m(见图1a),数值水槽在管线前后长度分别为3和3.7m,以保证数值计算完整地捕捉到管线附近的水动力特性变化。数值水槽宽度为0.8m,竖向高度为静水面以上5cm,数值水槽尺寸为:8.1m×0.8m×0.35m。
数值水槽网格划分采用分区多块结构网格,在水流方向上管线附近的水槽核心区域(-1 图1 水槽实验布置图 数值水槽左右两端分别为速度入口边界和出口边界,上方为自由出流边界,底部、两侧边壁和管线表面为固壁无滑移边界。数值计算中时间步长控制为自适应模式,初始步长为0.001s,最大库郎数为0.25,最大时间步长为0.1s,数值模拟时长为10s。采用高性能计算集群(80 CPUs ,AMD Opteron 6128, 2.0 GHz)进行并行计算。 2.1 物理模型实验布置 实验管线模型采用光滑有机玻璃管制成,外径50mm,壁厚5mm,水流作用角α=45°,直铺于床面。采用多普勒剖面流速仪(ADCP)测量管线附近的流速分布。测量位置如图1b所示。 2.2 模型验证 与物理实验工况条件相一致,对数值模型的可靠性进行验证。图2分别给出了管线上方(1#)、管前(2#)和管后(5#)位置垂直管轴向线方向流速分量u的垂线分布。 图2 管线附近位置垂线流速验证(e/D=0) 由图2可见,3个位置垂线流速分布的数值计算结果和实验结果基本一致。本文建立的斜向流作用下管线附近的三维水动力学模型可以准确的模拟管线附近的水流结构和研究水动力特性的变化规律。 3.1 作用角对管线附近水动力特性的影响 斜向水流作用下,管线周围流线具有明显的三维特性。图3为不同作用角水流作用下管线附近的三维流线,颜色标识为不同位置的涡量值。 由图3可见,与正向流相比(α=90°),斜向流作用下(α=30°~60°)管线附近的三维流线、紊动特性明显不同:(1)管前、管上和管后水流均有较大的沿管轴向下游流动的流速分量,进而导致管表面水流分离位置管轴向流速分量减小,相比正向流作用下此位置紊动强度明显减弱;(2)水流发生分离后,在管后形成大尺度的尾涡结构,并与管后沿管轴向下游水流耦合,形成沿管轴向下游逐渐拉伸的尾涡结构,而正向流作用下沿管轴向尾涡结构尺度基本不变;同时,斜向流作用下管后水体的紊动强度也相对偏弱;(3)斜向流作用下,随作用角的增大,管线阻水作用加强,水流沿管轴向的流速分量逐渐减小,法向流速分量增大,管线附近水流结构的三维特性减弱,管轴向各位置的尾涡结构开始沿管法向拉伸,水流紊动特性增强。 图3 水流作用下管线附近三维流线(e/D=0) 水流作用角的不同,管线中心法向立面的流场特性和涡量值分布呈现角度相关性规律,如图4所示。 建筑企业要考虑到建筑整体设计方案、使用方案、项目特点等多方面因素,进行合理招投标。在招投标时,设置一定的额度标准,对造价成本进行控制,从中选择最合理的方案。另外,还需要相关的管理部门积极参与,将经济方案与建筑方案相结合,选择出最经济实惠的方案,充分发挥其监督职能,明确资金流向。与此同时,建筑企业在对设计公司的选择时,需要询问专家意见,确保设计公司的选择的正确性,避免设计方面出现的不合理,造成建筑企业的经济损失。设计公司的正确选择,可以有助于顺利完成招投标,对建筑工程造价进行诸多方面的监控,有效控制建筑造价的成本控制。 由图4可见,随着作用角的增大(α=30°~60°),尾涡结构逐渐向后拉伸,中心位置随之后移(x/D=2~3),且尾涡在竖向上影响范围也有所扩大(z/D=1.2~1.6),同时管后负向涡量的分布范围和大小均逐渐加大。而在正向流作用下(α=90°),管后未形成完整的大尺度尾涡结构,但在z/D<2范围内出现稳定且较长(x/D>6)的紊流区域。 随着作用角的变化,位置管线附近的平面流场特性和涡量值分布也具有明显的角度相关性,本文重点分析了z/D=0.5的平面流场分布(图5)。 图4 立面水流结构图(e/D=0) 图5 z/D=0.5平面水流结构(e/D=0) 由图5所示,斜向流作用下管前和管后均出现明显的沿管轴向下游水流,管后轴向流范围远大于管前。随着作用角的增大,管前轴向流强度减弱,造成的紊流区域也逐渐缩小;而管后由于水流的管法向流速分量渐增大,管后各位置的尾涡结构加强轴向流虽也是逐渐减弱,紊流区域在上游管后方呈增大趋势。而正向流作用下,管后各位置均出现长度较长(x/D>15)且紊动强度较大的紊流区域,管线附近也未出现轴向流。 3.2 间隙比对水流结构的影响 斜向流作用下管线附近水流结构的三维特征明显,因而不同间隙比条件下管线附近的水动力特性也呈现与正向流作用的差异性。本文对作用角α=45°斜向流作用下不同间隙比e/D=0、0.1、0.3和0.5的管线模型进行计算,研究间隙比对斜向流作用下管线附近水动力特性的影响,如图6~7。 图6为不同间隙比条件下管线中心法向立面位置的流场特性和涡量分布。在e/D=0条件下,管后仅出现一个大尺度较为完整的负向尾涡结构,尾涡与几何边界(底床和管线表面)间的作用以边界层的剪切流作用为主。在间隙比较小条件下(e/D=0.1),管线下表面与底床间隙内形成高速强剪切流水体,以射流形式进入管后区域,对管上表面剪切流形成的尾涡结构造成冲击破坏,因而管后未出现较大尺度的尾涡结构,水流结构与高雷诺数下的圆柱绕流相似,管后形成充分发展的紊流区域。随着间隙继续增加(e/D≥0.3),间隙内管线下表面边界层形成的剪切流脱离底床边界层区域,且间隙流流态不同于较小间隙比条件(e/D=0.1)的射流型式,而是与管上表面的剪切流流态相似。在管线上表面和下表面剪切流的相互作用下,管后水流结构类似于圆柱绕流条件下的卡门涡街,且随着间隙比的增大(e/D=0.3~0.5)此流场结构越趋于明显。 图6 不同间隙比下立面水流结构 图7 不同间隙比下平面水流结构(z/D=0.1) 图7为斜向流作用下不同间隙比内在z/D=0.1位置的平面流场特性和涡量分布。在间隙比存在条件下(e/D=0.1~0.5)管线附近平面流场结构分区特征明显,在管前和管后区域均有明显的轴向流,且紊动强度较大,而在管线正下方约2D宽度范围内水流流向与斜向流的作用角相同,且流速值较大,紊动强度较小(e/D=0.1时平面z/D=0.1位于管线下表面边界层内)。间隙流流向不同于管前后轴向流的原因在于间隙内水体流速值较大、动水压强较小,而管前后水体的流速值相比较小、压强较大,且管前压强大于管后,所以在管前后压强梯度差的作用下间隙水体流向发生逆时针偏转,最终稳定于斜向流的作用角方向。 (1)随着作用角的增大,管线阻水作用加强,附近水流结构的三维特性减弱,尾涡结构逐渐向后拉伸和向上扩展,管后水流结构的紊动特性增强管前涡流范围逐步缩小至管线附近,管后涡流范围逐步向下游延伸,且管后涡漩尺度、回流范围与尾涡紊动区域逐步增加,尾涡中心逐步远离管线,且轴向水流逐渐减弱。 (2)受间隙比影响,管线附近平面流场结构区域特征明显,在管前和管后有明显的轴向流,但在管前后压强梯度差作用下,管下方水流流向保持与水流作用方向相同,流速值较大。 (3)管后尾涡的产生、脱落,涡旋尺度大小受e/D的影响明显。随着间隙比的增大,管线下表面形成的剪切流逐渐脱离底床边界层区域,间隙内射流现象消失,管后水流结构类似于圆柱绕流条件下的卡门涡街。 参考文献: [1]邱大洪, 王永学. 21世纪海岸和近海工程的发展趋势[J]. 自然科学进展, 2000, 11: 24-28. Qiu D H, Wang Y X. The trends of development in coastal and offshore engineering in the 21 century[J]. Progress in Natural Science, 2000, 11: 24-28. [2]Mao Y. The interaction between a pipeline and an erodible bed[J]. Series Paper Technical University of Denmark, 1987 (39): 26-31. [3]Sumer B M, Mao Y, Fredsøe J. Interaction between vibrating pipe and erodible bed[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, ASCE, 1988, 114(1): 81-92. [4]Moncada-M A T, Aguirre-Pe J. Scour below pipeline in river crossings[J]. Journal of Hydraulic Engineering, 1999, 125(9): 953-958. [5]Yang B, Gao F P, Wu Y X. Dimensional analysis and experimental apparatus on interaction between ocean current-pipeline and seabed[J]. Journal of Ship Mechanics, 2006, 10(3): 130-141. [6]Yang B, Gao F P, Jeng D S, et al. Experimental study of vortex-induced vibrations of a pipeline near an erodible sandy seabed[J]. Ocean Engineering, 2008, 35: 301-309. [7]Li F, Cheng L. Numerical model for local scour under offshore pipelines[J]. Journal of Hydraulic Engineering, 1999, 125(4): 400-406. [8]Brørs B. Numerical modeling of flow and scour at pipelines[J]. Journal of Hydraulic Engineering, 1999, 125(5): 511-523. [9]Liang D F, Cheng L. Numerical modeling of flow and scour below a pipeline in currents Part I. Flow simulation[J]. Coastal Engineering, 2005, 52: 25-42. [10]Ong M C, Utnes T, Holmedal L E, et al. Numerical simulation of flow around a circular cylinder close to a flat seabed at high Reynolds numbers using a k-ε model[J]. Coastal Engineering, 2010, 57(10): 931-947. [11]Li F, Cheng L. Predietion of lee-wake seouring of pipelines in currents[J]. J. of Waterway, Port, Coastal, and Oeean Engineering, 2001, 127(2):106-112. [12]Speziale C G. Computing non-equilibrium turbulent flows with time-dependent RANS and VLES[C]//Fifteenth International Conference on Numerical Methods in Fluid Dynamics. Berlin Heidelberg: Springer 1997: 123-129. [13]Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[J]. Advances in DNS/LES, 1997, 1: 4-8. [14]Spalart P R, Deck S, Shur M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and computational fluid dynamics, 2006, 20(3): 181-195. [15]Verhoeven O. Trailing Edge Noise Simulations[D]. Decft: Delft University of Technology, 2011. 责任编辑陈呈超 基金项目:❋ 国家自然科学基金项目(51239001,41176072)、湖南省教育厅科研项目(15C0048)和长沙理工大学人才计划项目 收稿日期:2015-04-10; 修订日期:2015-12-10 作者简介:常留红(1979-),女,讲师,博士。E-mail:claire886@163.com 中图法分类号:TV139.2 文献标志码:A 文章编号:1672-5174(2016)07-105-06 DOI:10.16441/j.cnki.hdxb.20150366 Experimental Study on the Hydrodynamics Around Marine Pipelines Under Oblique Flows CHANG Liu-Hong1, JIANG Chang-Bo1,2, CHENG Yong-Zhou1,2 (1. School of Hydraulic Engineering, Changsha University of Science & Technology; 2. Hunan Province Key Laboratory of Water, Sediment Sciences & Flood Hazard Prevention, Changsha 410004,China) Abstract:The hydrodynamic characteristics around marine pipeline are main causes of scour. A 3D numerical flume was developed based on the open-source software and the turbulence model of detached eddy simulation.The accuracy and reliability of numerical model was validated by laboratory results of velocity profile around pipelines. The influences of flow incident angle (30°、45°、60°and 90°) and the gap ratio (0、0.1、0.3、0.5) on 3D hydrodynamic characteristics around pipeline wereanalyzed.SNumerical results show that3D hydrodynamic characteristics are gradually weakened, trailing vortex extending leeward and upward, and the turbulence region enlarging at upstream with the increase of flow incident angle;with the extension of gap radio, jet flow in the gap is gradually disappeared, fluid structure behind pipeline similar to the one behind cylinder under steady flow; obvious different fluid structure around pipeline is found in different region, distinct axial flow found at seaward and leeward of pipeline, nevertheless, the same flow direction to flow incident anglefound below pipeline. Key words:submarine pipelines; oblique flows;hydrodynamic characteristics;angle of action;gap ratio Supported by the National Natural Science Foundation of China (51239001, 41176072), the Scientific Research Project of Hunan Provincial Department of Education(15C0048) and the Changsha University of Science and Technology Talent Program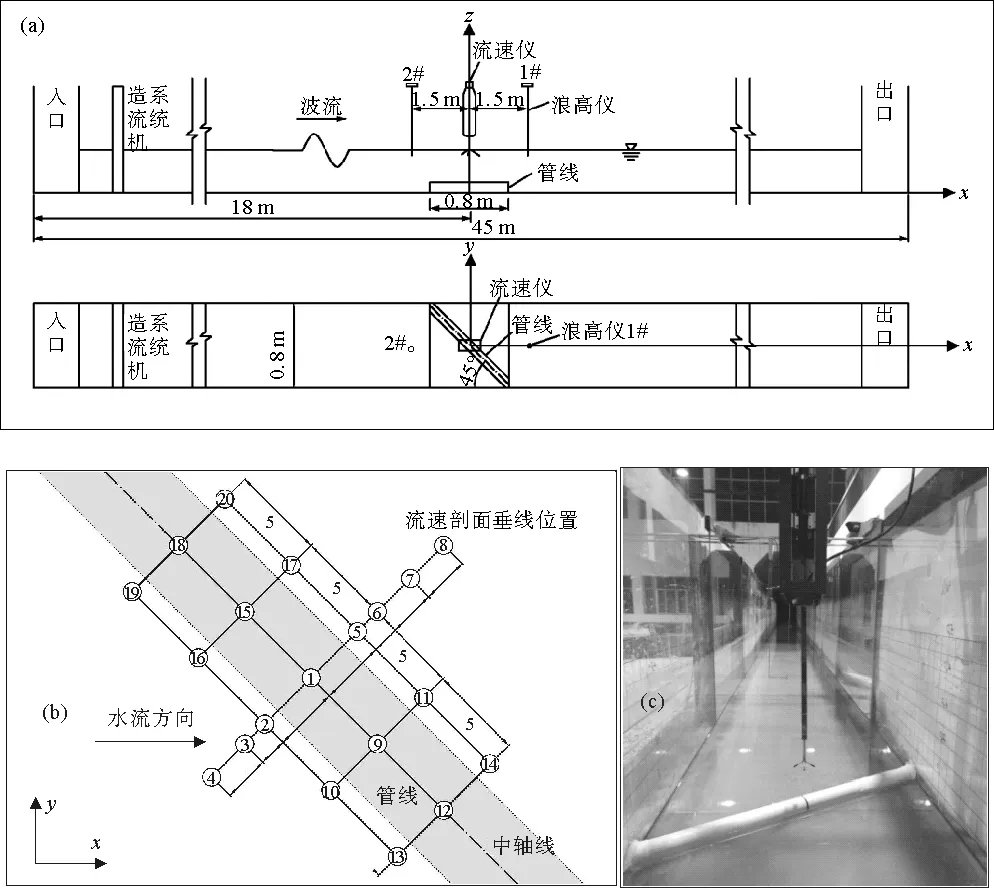
2 模型验证
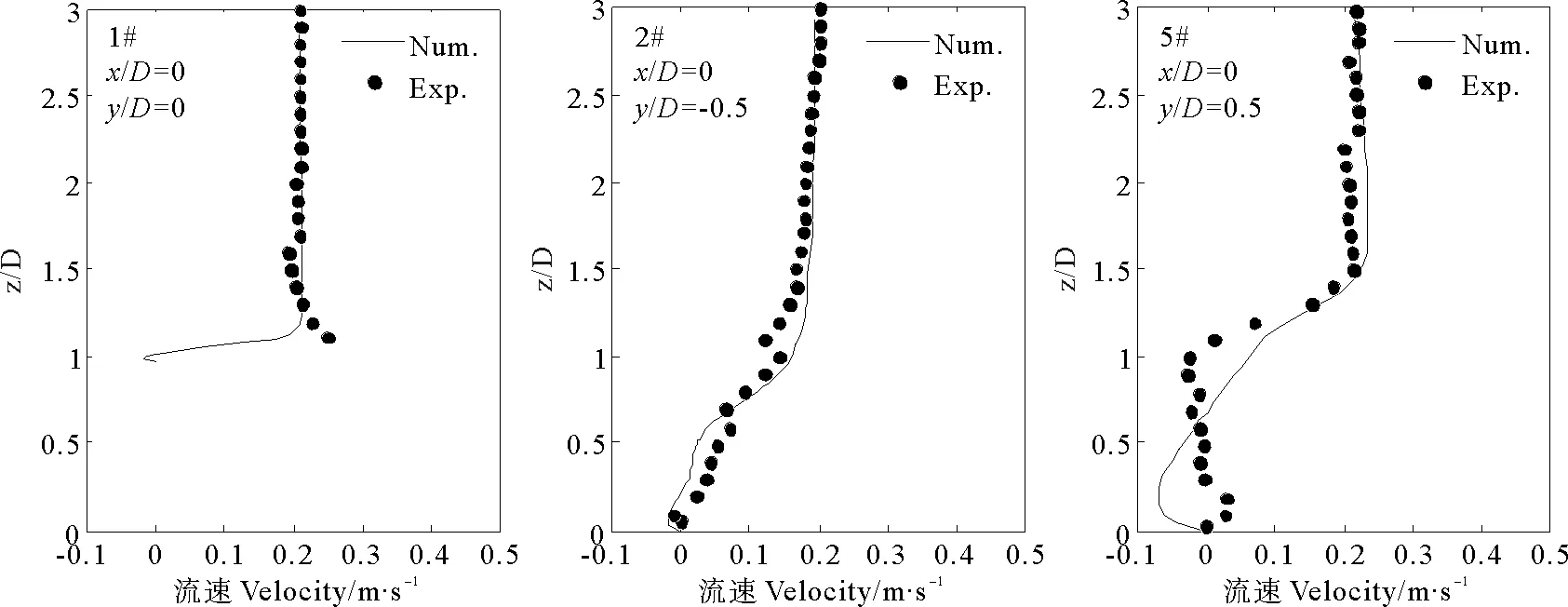
3 结果与分析

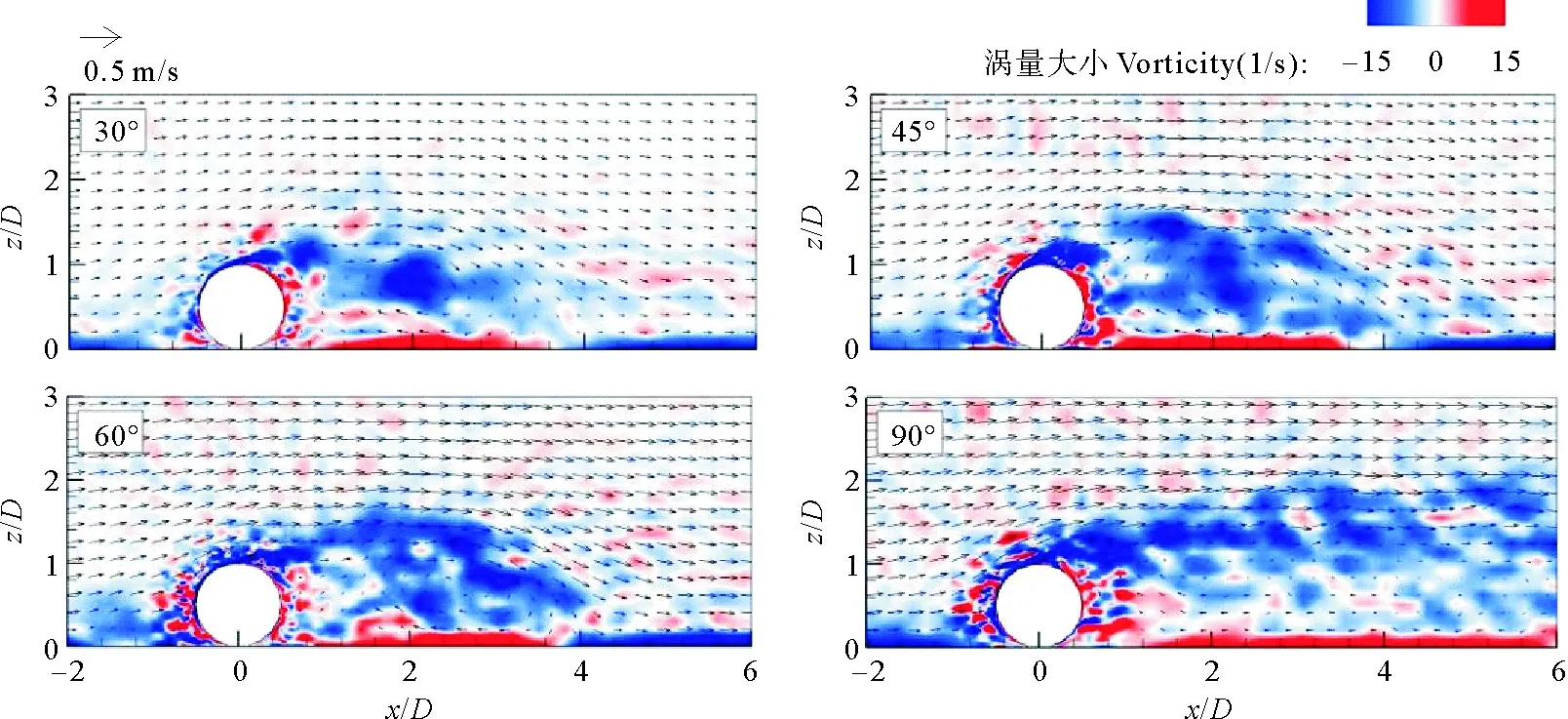
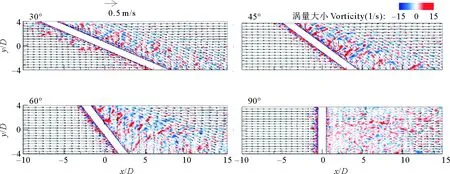
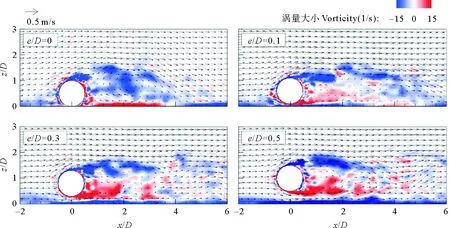
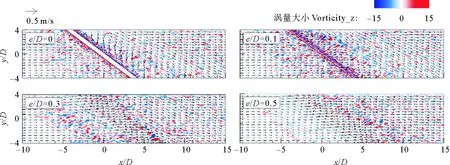
4 结论
