多通道带乘性噪声2-D广义系统状态最优估计算法❋
2016-08-13杨荣荣
张 玲, 刘 川, 杨荣荣
(中国海洋大学工程学院, 山东高校海洋机电装备与仪器重点实验室,山东 青岛 266100)
多通道带乘性噪声2-D广义系统状态最优估计算法❋
张玲, 刘川, 杨荣荣
(中国海洋大学工程学院, 山东高校海洋机电装备与仪器重点实验室,山东 青岛 266100)
摘要:2-D系统及其广义系统在图像处理,电力网络等领域有着广泛的应用,本文基于多通道带乘性噪声的2-D 广义Roesser模型提出一套状态最优估计算法。在以往基于2-D广义系统的研究中乘性噪声因子多假设是一维随机序列,本文的乘性噪声因子是对角矩阵,矩阵对角线上每个元素都是一维随机序列,这意味着系统不仅具有多个观测通道而且每个观测通道都受到不同乘性噪声的影响,更加符合实际情况,能够解决系统在更加复杂环境中的状态估计问题。仿真结果验证了该算法的有效性。
关键词:多通道;乘性噪声;2-D系统;广义系统;最优估计
引用格式:张玲, 刘川, 杨荣荣.多通道带乘性噪声2-D广义系统状态最优估计算法[J].中国海洋大学学报(自然科学版), 2016, 46(7):124-129.
ZHANG Ling, LIU Chuan, YANG Rong-Rong.Optimal state estimation algorithm for 2-D generalized system with multi-channel multiplicative noise[J].Periodical of Ocean University of China, 2016, 46(7):124-129.
广义系统的研究始于上世纪七十年代,与正常系统相比广义系统不仅能够描述对象的动态特性,同时也描述了对象的静态特性,因此有着更加广泛的应用。上世纪八十年代末波兰学者Kaczorek在2-D广义系统研究领域作出了奠基性的贡献,2-D广义系统在电力网络、化学过程、经济系统和生物系统等领域有着广泛的应用[1]。各国专家学者对2-D广义系统的稳定性[2-4]、鲁棒性[5-6]、能控能观性[7]等问题展开了深入的研究,取得了丰富的理论成果,建立起较为完善的2-D广义系统理论。
自卡尔曼滤波提出以来,经过40多年的发展,卡尔曼滤波已经形成了一个比较完整的理论体系。将卡尔曼滤波扩展至2-D系统是一项富有意义的工作,科研人员基于2-D系统状态空间模型提出了不同的状态最优估计算法,比如:斜割支线法[8]、逐行扫描法[9-10]等方法。
然而,上述提到的算法仅适用于受加性噪声干扰的2-D离散系统,实际中的系统往往受到时变性、非线性等因素的干扰,这些因素有时可以近似归结为乘性噪声。乘性噪声存在于通信系统[11],图像处理[12]等诸多领域。本文将2-D广义系统的乘性噪声因子推广至对角随机矩阵,矩阵对角线上每个元素都是一维随机序列[13],这意味着系统不仅具有多个观测通道而且每个观测通道都受到不同乘性噪声的影响,适用于解决在更加复杂环境中的系统状态估计问题。
本文针对多通道带乘性噪声2-D广义Roesser模型,将其等价变换为2个子系统,其中一个子系统可以整理为多通道带乘性噪声的2-D FM-Ⅱ模型[1]。基于投影定理我们通过推导可获得FM-Ⅱ模型的状态最优估计算法并利用其与2-D广义Roesser模型的变换关系,进一步得到多通道带乘性噪声的2-D广义 Roesser模型的状态最优估计算法。上述算法在线性最小方差意义下是最优的。
1 问题描述
考虑以下多通道带乘性噪声2-D广义 Roesser模型:
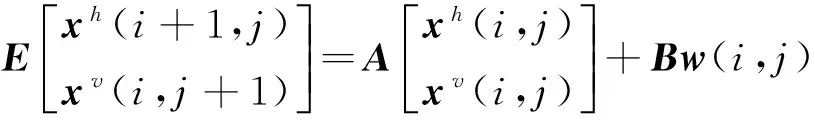
(1)
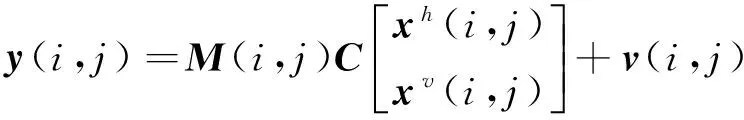
(2)
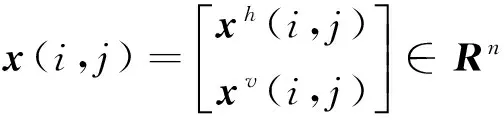
设系统满足以下条件:
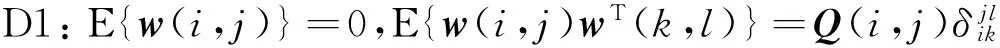
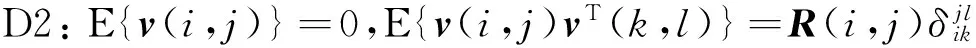
D3:E{M(i,j)}=U(i,j),
M(i,j)=diag(m11(i,j),…,mmm(i,j)),
U(i,j)=diag(u11(i,j),…,umm(i,j)),
N(i,j)=

D4:E{x(0,j)}=0,E{x(0,j)xT(0,l)}=P(0,j)δjl,
E{x(i,0)}=0,E{x(i,0)xT(k,0)}=P(i,0)δik,
E{x(i,0),x(0,j)}=0,(i,j)≠(0,0);
D5:随机序列{x(i,0),x(0,j)}、{w(i,j),v(k,l)}和M(i,j)在统计上相互独立。
上述条件在实际情况中比较容易满足:D1和D2表明w(i,j)和v(i,j)是零均值高斯噪声;D3允许乘性噪声矩阵的每个元素在坐标同一位置统计相关,描述了更加复杂的通道特性;D4表明边界随机变量符合高斯分布并且不同位置的边界随机变量统计不相关;D5表明w(i,j),v(i,j)和M(i,j)在统计上相互独立。
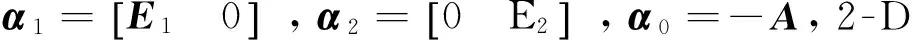
α1x(i+1,j)+α2x(i,j+1)+α0x(i,j)=Bw(i,j)。
(3)
其中:r1=rank(α1);r2=rank(α2);r3=n-r1-r,称系统(3)为2-D广义系统的扩展Roesser模型。
参考文献由[1]知,对于无跳跃模的系统(3),令,存在非奇异矩阵F和H,使系统(2)(3)等价变换为:
(4)
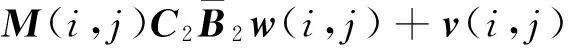
(5)
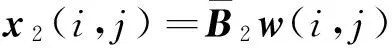
(6)
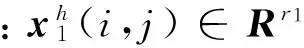
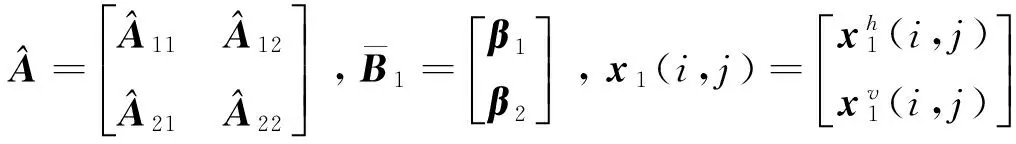
x1(i,j)=A1x1(i,j-1)+A2x1(i-1,j)+
B1w(i,j-1)+B2w(i-1,j)。
(7)

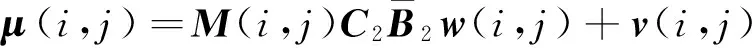
y(i,j)=M(i,j)C1x1(i,j)+μ(i,j)。
(8)
Ω(i,j)=E{μ(i,j)μT(k,l)}=

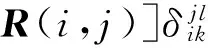
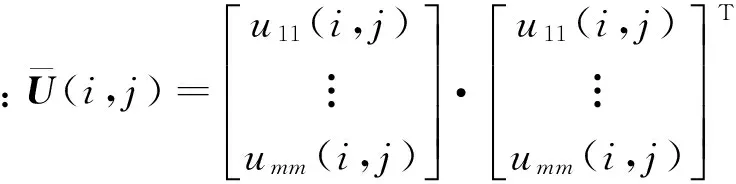
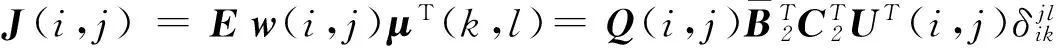
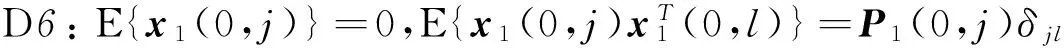

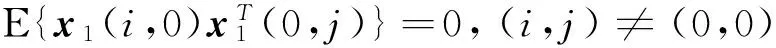
由此可见,多通道2-D广义系统可以通过受限等价变换为一个低阶多通道2-DFM-Ⅱ模型,以及另一个由w(i,j)组成的低阶子系统。多通道2-D广义系统的状态最优估计问题就转化为对动态噪声w(i,j)和多通道2-DFM-Ⅱ模型状态的最优估计问题。
2 状态最优估计算法
系统(6)~(8)可由系统(1)(2)变换得到,首先对系统(6)~(8)进行状态最优估计算法的推导。
为了方便推导,以下结论首先以引理的形式给出。
引理针对系统(6)~(8),有如下结论成立。
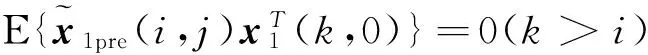
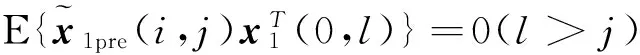

由系统的边界特性易知引理是正确的,此处略去证明。
定理1系统(6)~(8)若满足之前假设条件,则有如下在线性最小方差意义下的状态最优估计算法。
x1(i,j)的估计值
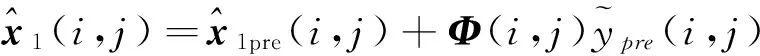
(9)
x1(i,j)的估计预测值

(10)
x1(i,j)的估计误差方差阵
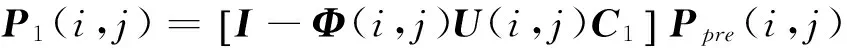
(11)
x1(i,j)的预测误差方差矩阵
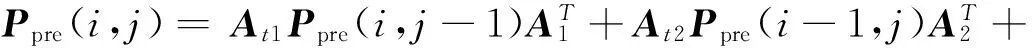
(12)
动态噪声估计值:
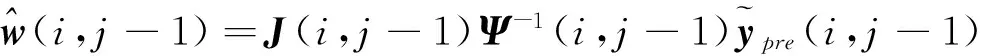
(13)
动态噪声估计误差方差阵
Pw(i,j)=Q(i,j)-J(i,j)Ψ-1(i,j)JT(i,j),
(14)
x2(i,j)的估计值

(15)
x2(i,j)的估计误差方差阵

(16)
其中:
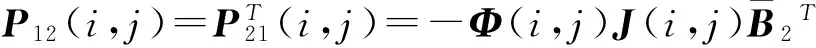
(17)
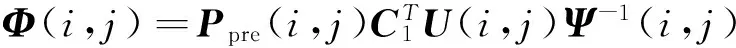
(18)
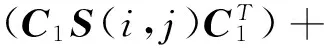
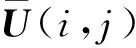
(19)

(20)
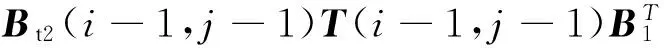
(21)
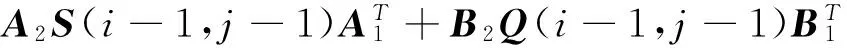
(22)
Bt1(i,j-1)=A1Φ(i,j-1)+B1J(i,j-1)Ψ-1(i,j-1),
At1(i,j-1)=A1-Bt1(i,j-1)U(i,j-1)C1,
Bt2(i-1,j)=A2Φ(i-1,j)+B2J(i-1,j)Ψ-1(i-1,j),
At2(i-1,j)=A2-Bt2(i-1,j)U(i-1,j)C1。
初值:
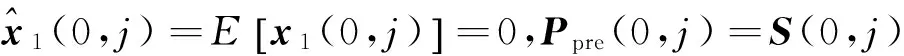

定理1给出了系统(6)(7)(8)的状态最优估计算法,基于上述算法,系统(1)(2)的状态最优估计算法可以相应得到。
证明记Y(i,j)为y(0,0),…,y(0,j);y(1,0),…,y(1,j);y(i,0),…,y(i,j)张成的线性空间,Y-1(i,j)为Y(i,j)去除向量y(i,j)后的所有观测向量张成的空间。
由μ(i,j)的统计特性知:μ(i,j)⊥Y-1(i,j),y(i,j)在线性空间Y-1(i,j)上的投影即观测向量的预测值为:
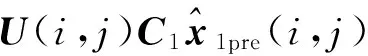
(23)
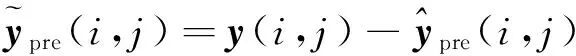

(24)
新息方差阵 :

(25)
把式(24)代入上式可得式(19)。
状态向量的预测值为x1(i,j)在观测序列Y-1(i,j)上的投影

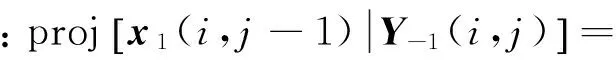
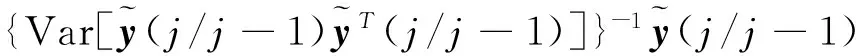
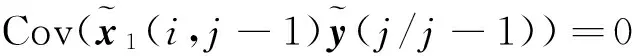
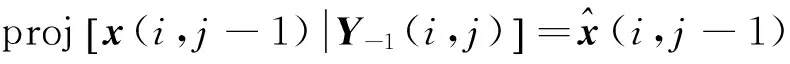
(26)
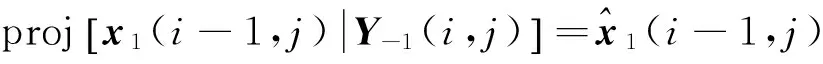
(27)
由w(i,j)的统计特性可得
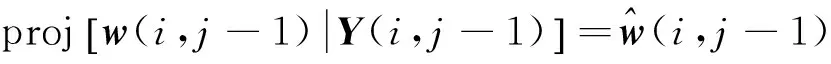
(28)
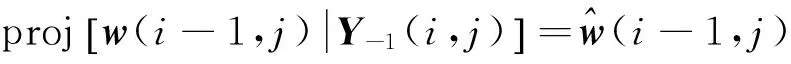
(29)
则由(26)~(29)可得式(10)。
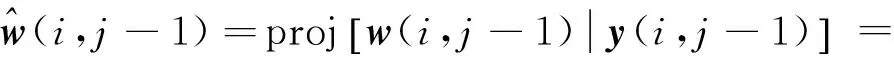
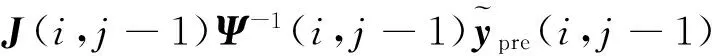
(30)
即式(13)得证。
状态的预测误差为
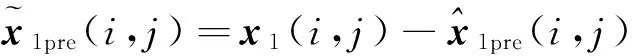
(31)
则由上式和(24)式可得
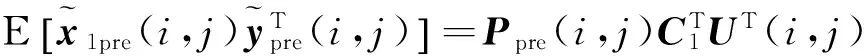
(32)
由投影定理得x1(i,j)的状态估计值:
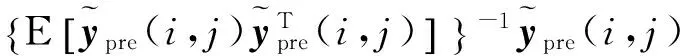
把式(25)和式(32)代入上式,记作
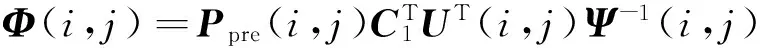
得式(9)和式(18)。
把式(9)、(13)和式(18)代入式(10)可得
Bt2(i-1,j)y(i-1,j),
(33)
则可得
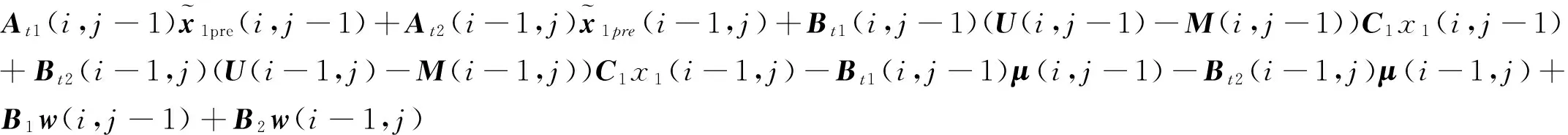
(34)
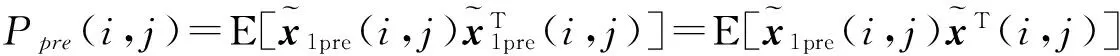
把式(34)和式(7)代入上式得式(12)。同理由式(34)和式(7)也可得式(21)。
(35)


(36)
把式(9)、(24)代入式(35)可得
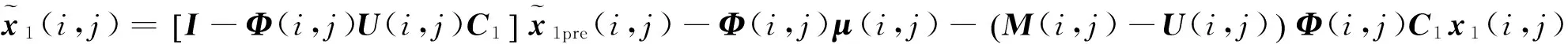
(37)
把上式和式(7)代入式(36),则式(11)得证。
由式(6)可得式(15)。则
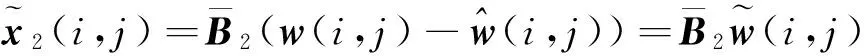
(38)
把式(13)代入上式可得式(14)。
把式(37)和式(38)代入
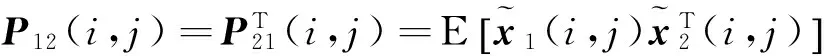
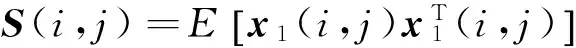
至此定理1得证。
定理2系统(1)(2)若满足假设条件D1~D5,且无跳跃模,则有如下在线性最小方差意义下最优的状态估计算法。
状态最优估计值
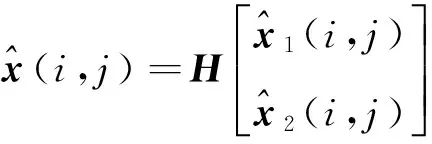
(39)
状态估计误差方差矩阵
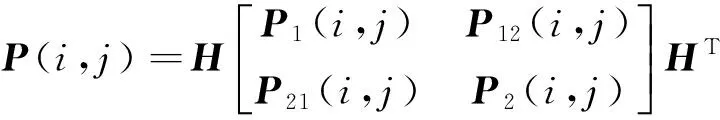
(40)
证明
将(39)代入下式,可得
3 数值仿真
以三阶系统为例,来验证本文提出的状态最优估计算法的有效性。为了计算方便,假设Q,R,U,T统计特性是时不变的。
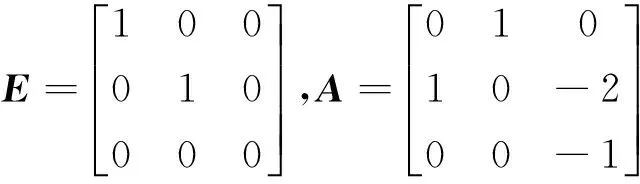
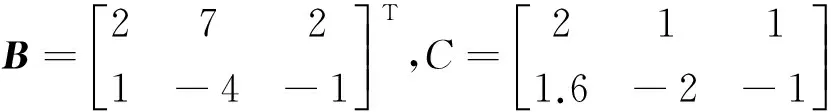
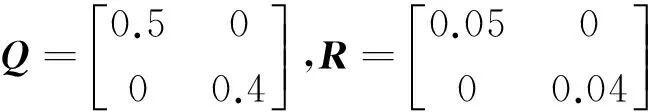
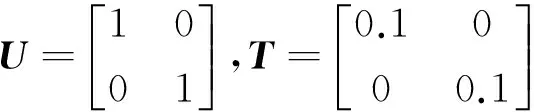
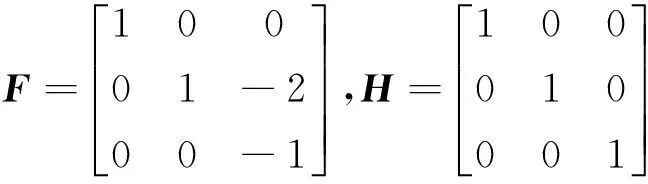
其中:E,A,B及C是相应维数的系统矩阵;Q是动态噪声的方差矩阵;R是观测噪声的方差矩阵;U和T是乘性噪声矩阵的均值及方差矩阵;F和H是系统等价变换的非奇异矩阵。
在此例中,x(i,j)是3维状态向量,x(i,j)第一分量三维理论值和估计值的横截剖面图如图1所示,x(i,j)第一分量三维理论值和估计值横截剖面图的绝对误差如图2所示。
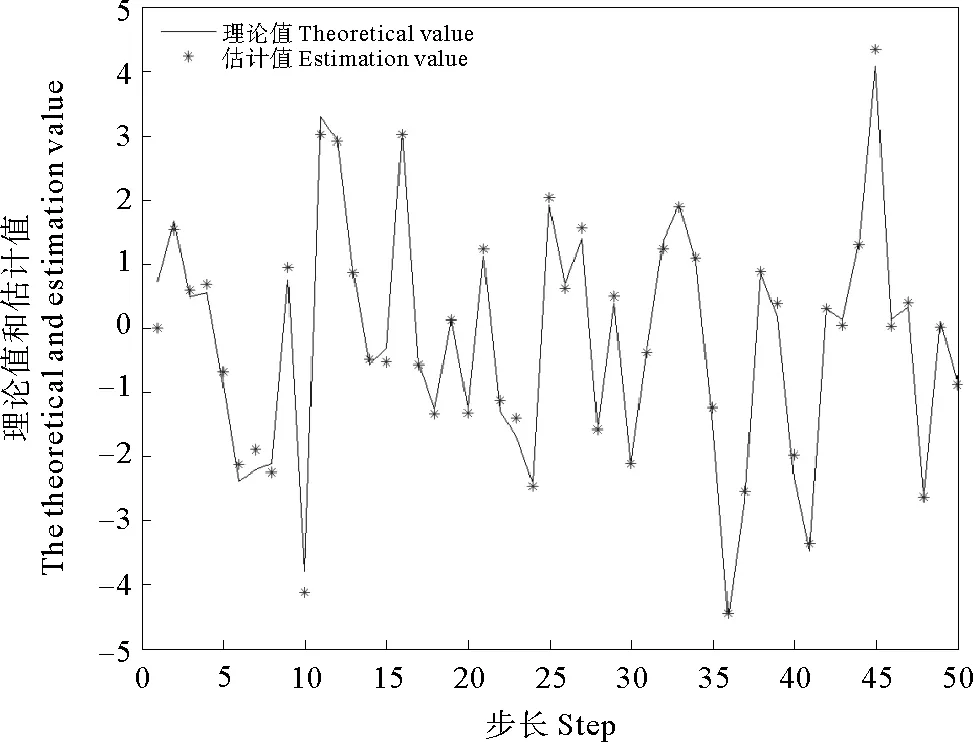
图1 x(i,j)第一分量三维理论值和估计值的横截剖面图
由于系统具有多个观测通道且每个观测通道都受到不同乘性噪声的影响,使2-D广义系统的状态观测受到更加复杂因素的影响,图2表明状态估计值可以较好的跟踪系统状态的理论值。上述仿真结果验证了所提出的多通道2-D广义系统状态最优估计算法的有效性。

图2 x(i,j)第一分量三维理论值和估计值横截剖面绝对误差
4 结语
本文针对多通道带乘性噪声2-D广义系统提出了其状态最优估计算法,首先通过2-D广义系统的受限等价变换得到一个低阶多通道2-D FM-Ⅱ模型,以及另一个由动态噪声组成的低阶子系统,之后推导出以上2个子系统的状态最优估计算法,最后利用2-D模型之间的受限等价变换关系得到2-D广义系统的状态最优估计算法。该算法可以应用到更加复杂的环境中,解决系统在更加复杂环境中的状态估计问题。仿真结果表明系统状态估计值与理论值可以较好地吻合,验证了算法的有效性。
[1]邹云, 王为群, 徐胜元. 2-D奇异系统理论 [M]. 北京: 科学出版社, 2012.
Zou Yun, Wang Weiqun, Xu Yuansheng. 2-D Singular System Theory[M]. Beijing: Science and Technology Publishing House, 2012.
[2]Kaczorek Tadeusz. Stabilization of singular 2-D continuous-discrete systems by state-feedback controllers [J]. IEEE Transactions on Automation Control, 1996, 41(7): 1007-1009.
[3]Zou Yun, Xu Xuiling, Wang Weiqun. Stability for two-dimensional singular discrete systems described by general model [J]. Multidimensional Systems and Signal Processing, 2008, 19(2): 219-229.
[4]Zou Yun, Campbell S L. The jump behavior and stability analysis for 2-D singular systems [J]. Multidimensional Systems and Signal Processing, 2000, 11(4): 339-358.
[5]Zou Yun, Xu Xuiling, Xu Shengyuan et al. Bounded real lemma and robust H∞ control of 2-D singular Roesser models [J]. System&Control Letters, 2005, 54(4): 339-346.
[6]Xu H L, Xu S Y. Robust Stabilization of 2-D Uncertain Singular Roesser Models [C]. IEEE: Control, Automation, Robotics and Vision Conference, 2004, 2: 1476- 1480.
[7]Zou Yun, Wang Weiqun, Xu Xuiling. The state observer and compensator of a large class of 2-D acceptable singular systems [J]. Multidimensional Systems and Signal Processing, 2008, 19(1): 139-155.
[8]陈雪如, 杨成语. 随机2-D FMⅡ模型的状态估计 [J]. 自动化学报, 2001, 27(1): 131-135.
Chen Xueru, Yang Chengyu. The State Estimation of Stochastic 2-D FM Model [J]. ACTA AUTOMATICA SINICA , 2001, 27(1): 131-135.
[9]Zou Yun, Sheng Mei, Zhong Ningfang, et al. A generalized kalman filter for 2-D discrete systems [J]. Circuits Systems Signal Processing, 2004, 23(5): 351-364.
[10]盛梅, 邹云. 广义2-D Roesser模型的状态滤波器 [J]. 兵工学报, 2006, 27(3): 432-436.
Sheng Mei, Zou Yun. The State Filter of Generalized 2-D Roesser Model [J]. Acta Armamentarii, 2006, 27(3): 432-436.
[11]Chu Dongsheng, Gao Shouwan, Guo Lina. State estimation for multi-channel stochastic singular systems with multiplicative noise [J]. Asian Journal of Control, 2010, 12(6): 725-733.
[12]Bioucas-Dias J M, Figueiredo M A T. Multiplicative noise removal using variable splitting and constrained optimization [J]. IEEE Transactions on Image Processing, 2010, 19(7): 1720-1730.
[13]褚东升, 韩慧, 刘滨. 噪声相关时多通道带乘性噪声系统最优滤波 [J]. 青岛海洋大学学报, 2001, 31(5): 782-788.
Chu Dongsheng, Han Hui, Liu Bin. The optimal filter of muti-channel system with multiplicative noise under the circumstance of related Noise [J]. Journal of Ocean University of Qingdao, 2001, 31(5): 782-788.
责任编辑陈呈超
基金项目:❋ 国家自然科学基金项目(41506114; 51279185); 山东省自然科学基金项目(ZR2010DQ003)
收稿日期:2014-10-12;
修订日期:2015-08-10
作者简介:张玲,女,博士,副教授。主要研究方向:智能控制与智能信息处理。E-mail:zljoan@163.com
中图法分类号:TN929.3
文献标志码:A
文章编号:1672-5174(2016)07-124-06
DOI:10.16441/j.cnki.hdxb.20140350
Optimal State Estimation Algorithm for 2-D Generalized System with Multi-Channel Multiplicative Noise
ZHANG Ling, LIU Chuan, YANG Rong-Rong
(College of Engineering, Ocean University of China, Key Laboratory of Marine Mechanical and Electrical Equipment & Instruments of Shandong Provincial Universities, Qingdao 266100,China)
Abstract:The two-dimensional (2-D) system and it’s generalized model are widely used in many fields such as image processing, power grid. The system state of the two-dimensional (2-D) state space model is the function of two independent variables. With the expansion of the scope of study objects for modern control theory, the research achievement based on 2-D state space model is becoming more and more abundant. The multiplicative noise is widely existed in the problems studied in 2-D model, for instance, the salt-and-pepper noise in the territory of image processing. In this paper, a set of optimal state estimation algorithm is proposed for 2-D generalized Roesser model with multi-channel multiplicative noise. In previous research on the 2-D generalized system, the multiplicative noise factor is usually assumed as a scalar stochastic sequence. In this paper, the multiplicative noise factor is a diagonal matrix, whose elements in the diagonal matrix are scalar stochastic sequences, which means the system is not only multi-channel but also each channel is interfered by different multiplicative noises. The system model and the corresponding optimal estimation algorithm can be flexibly applied for the state estimation problem in more complicated environment. The algorithm has recursive structure and can overcome the problem of “dimensional disaster” in previous method by adopting line by line state filtering sequence. The algorithm is convenient for realization on computer due to low computational complexity. The simulation results verified the effectiveness of the proposed algorithm.
Key words:multi-channel; multiplicative noise; 2-D system; generalized system; optimal estimation
Supported by National Natural Science Foundation of China (41506114; 51279185); Natural Science Foundation of Shandong Province (ZR2010DQ003)
