摆线钢球行星传动自由振动分析

杨荣刚　安子军　段利英

燕山大学，秦皇岛，066004



摆线钢球行星传动自由振动分析

杨荣刚安子军段利英

燕山大学，秦皇岛，066004

摘要：为准确反映摆线钢球行星传动的固有特性，建立了平移-扭转耦合动力学模型，求解了载荷作用时各构件相对位移量，并推导出动力学微分方程，获得了自由振动特征方程，得到了系统固有频率及主振型。分析了结构参数对固有频率的影响，并对理论研究进行了验证。结果表明：机构具有系统全振动模态、输出轴静止振动模态与输出轴扭转振动模态，传动比对固有频率的影响具有不确定性，输出轴支承刚度是影响固有频率的重要参数，验证了理论研究的正确性。

关键词：摆线钢球行星传动；自由振动；四点啮合；模态分析；轴向预紧

0引言

摆线钢球行星传动无侧隙啮合副形成的“无侧隙啮合”，使其成为精密传动中非常重要的高性能传动机构。该传动机构具有实时无侧隙传动、啮合效率高、噪声低、结构紧凑、结构易于微型化等突出特性，在航空遥感相机位移补偿传动机构及频繁往复抓取工件的机器人伺服传动机构等高精密传动应用领域有着重要价值和发展前景[1-2]。

文献[3-4]对摆线钢球行星传动进行了较深入的理论研究，并应用于精密机械伺服传动机构。文献[5]在忽略非传力接触点的基础上，利用超静定方法建立啮合副非线性力学模型，对啮合副进行静力学分析。文献[6]将质量较小的活齿简化为无质量的弹簧，建立平移-扭转耦合动力学模型，揭示了系统的固有特性。摆线钢球行星传动在间隙调节机构轴向预紧力作用下，能够实现啮合副无隙啮合传动(啮合副实时四点接触)。同一啮合点在传力与非传力两种状态间转换，法向力曲线连续且光滑，因此建立四点接触力学模型更符合实际情况。对活齿传动机构进行动力学建模时需考虑活齿[7-9]，忽略活齿将会影响固有频率与主振型计算的结果的精确性。因此，建立考虑啮合副四点接触与活齿的新型力学模型，并重新进行固有频率及主振型的求解有一定的实际意义。

在初始轴向预紧力作用下，通过得到的啮合点静态变形量，求解工作载荷作用下的啮合点相对位移量，建立考虑活齿及啮合副四点接触的摆线钢球行星传动平移-扭转耦合动力学模型，推导微分方程组，求解固有频率与模态向量，分析了参数对固有频率的影响，对理论研究进行了试验验证。

1耦合动力学模型建立

摆线钢球传动的结构如图1a所示。图1b所示为等速啮合副环形槽为双圆弧环形槽的结构，该结构能够实现机构的无隙啮合传动。图1中，β1、β2分别为环形槽外侧、内侧啮合点法线与盘平面的夹角，r1、r2分别为环形槽外侧、内侧纵切面曲率半径。

(a)结构简图1.中心盘　2.减速钢球　3.行星盘　4.输入轴　5.输出轴(盘) 　6.等速钢球

(b)双圆弧环形槽结构图图1　摆线钢球行星传动结构图

中心盘右侧加工有外摆线槽，行星盘左侧加工有内摆线槽，内外摆线槽轴向重合位置处放置减速钢球。行星盘右侧与输出轴左侧加工有相同数量的环形槽，环形槽轴向重合位置处安装等速钢球。运转时，输入轴偏心段带动行星盘平动，行星盘挤压减速钢球。钢球在中心盘摆线槽的限制作用下反推行星盘，使行星盘以较低的转速转动，实现转速的变化。行星盘通过等速钢球将转速等速传递给输出轴，实现转速的等速输出。输出轴受到间隙调节结构预紧作用，轴向微移动δx，产生一定轴向预紧力，使减速啮合副与等速啮合副实现实时的四点接触。

1.1耦合动力学模型

借鉴行星齿轮传动振动的研究成果[10-11]，建立摆线钢球行星传动减速啮合副与等速啮合副耦合的平移-扭转耦合动力学模型。分析中假设如下:①忽略运动过程中各构件的轴向振动；②将系统简化为集中参数模型，各轴承及啮合副均简化为无质量线弹簧，其余构件简化为刚体；③钢球与槽之间的啮合力作用在啮合平面内，平面与轴线平行；④不考虑支承轴承对系统施加的外载荷及各构件之间摩擦力的作用，并忽略各处的阻尼。

考虑输入轴、中心盘、行星盘与输出轴的平移、扭转自由度及钢球的平移自由度，建立平移-扭转耦合动力学模型，如图2、图3所示。

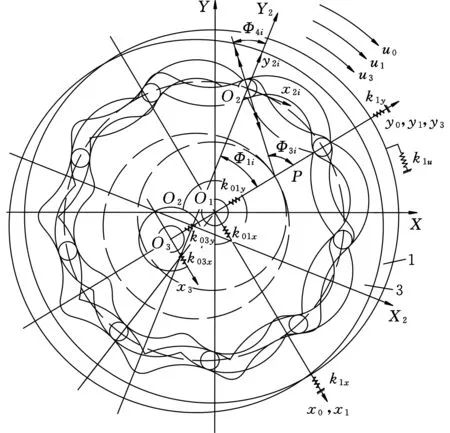
(a)减速啮合副相对位移图

(b)前半周期相对位移(c)后半周期相对位移图2　减速啮合副动力学模型

(a)等速啮合副相对位移

(b)前半周期相对位移(c)后半周期相对位移图图3　等速啮合副动力学模型

图2、图3中，Φ1i为第i个减速钢球绕输入轴坐标系逆时针转过的角度，Φ3i为第i个减速钢球法平面绕输入轴坐标系逆时针转过的角度，Φ4i为第i个减速钢球法平面绕该钢球坐标系逆时针转过的角度，O1XY为固定坐标系，O2X2Y2为与减速钢球系固连的减速钢球坐标系，O1x0y0为与输入轴固连的输入轴坐标系，O3x3y3为与行星盘固连的行星盘坐标系。O2ix2iy2i为第i个减速钢球坐标系，O2ix2iy2i的两坐标轴与O1X2Y2两坐标轴平行。O4jx4jy4j为第j个等速钢球坐标系，O4jx4jy4j的两坐标轴与O1x0y0两坐标轴平行。xi、yi(i=0,1,3,5,21,22,…,2(Z2-1),2Z2,41,42,…, 4(Z4-1),4Z4)为由于振动构件质心偏离理论位置的线位移，u0、u1、u3、u5为由振动产生的角位移。如果不做说明，脚标0、1、3、5、2i与4i均分别指中心盘、输入轴、行星盘、输出轴、第i个减速钢球与第i个等速钢球。Z2、Z4分别为减速与等速钢球个数。φj为第j个等速钢球绕输入轴坐标系y5轴逆时针转过角度。

1.2啮合点相对位移

间隙调节机构产生初始轴向预紧力(未加载工作载荷)时，使行星盘相对于中心盘轴向微移动δ1x，减速啮合副啮合点A1、B1、C1、D1处变形量分别为

式中，k1、k2、k3、k4分别为啮合点A1、B1、C1、D1处的啮合刚度；β为啮合点法线与盘平面夹角。

初始预紧力使输出轴相对于行星盘轴向微移动δ2x。等速啮合副中，啮合点A2与D2、B2与C2变形量相同：

由图2中各构件之间的相对位置关系可知，机构加载工作载荷时，减速啮合副中第i个钢球与摆线槽在啮合点A1、B1、C1、D1处的压缩量分别为

δAi=δ1-(δ2i+u3Z3esinΦ3i+

x3sinΦ3i-y3cosΦ3i)cosβ

δBi=δ2+(δ2i+u3Z3esinΦ3i+

x3sinΦ3i-y3cosΦ3i)cosβ

δCi=δ3-(δ2i+u1Z3esinΦ3i+

x1sinΦ3i-y1cosΦ3i)cosβ

δDi=δ4+(δ2i+u1Z3esinΦ3i+

x1sinΦ3i-y1cosΦ3i)cosβ

δ2i=-x2isinΦ4+y2icosΦ4

式中，Z3为内摆线槽齿数；e为输入轴偏心距一半。

加载工作载荷时，等速啮合副中第j个钢球与环形槽在A2、B2、C2、D2处的相对位移分别为

δdAj=δA+y4jcosβ1-u3Rwsinφjcosβ1-y3cosβ1

δdBj=δB-y4jcosβ2+u3Rwsinφjcosβ2+y3cosβ2

δdCj=δB+y4jcosβ2-u5Rwsinφjcosβ2-y5cosβ2

δdDj=δA-y4jcosβ1+u5Rwsinφjcosβ1+y5cosβ1

式中，Rw为等速钢球所在圆半径。

输入轴偏心段与行星盘相对位移为

δ03x=x0-2eu0-x3

1.3各构件动力学微分方程

由输入轴与中心盘、行星盘之间的相对位移关系，建立输入轴动力学微分方程：

(1)

式中，ωr为输入轴转速；Tr输入轴转矩；k01x、k03x分别为中心盘与输入轴、中心盘与行星盘x方向支承刚度；k01y、k03y分别为中心盘与输入轴、中心盘与行星盘y方向的支承刚度。

由第i个减速钢球与中心盘、行星盘之间的相对位移关系，建立第i个减速钢球动力学微分方程：

(2)

式中，ω2为减速钢球转速。

由中心盘与输入轴、减速钢球之间的位移关系，建立中心盘动力学微分方程：

(3)

式中，k1x、k1y分别为x轴、y轴方向支承刚度；k1u为扭转刚度。

由行星盘与输入轴、减速钢球、等速钢球之间的相对位移关系，建立行星盘动力学微分方程：

(4)

由第j个等速钢球与输出轴、行星盘之间的相对位移关系，建立第j个等速钢球的动力学微分方程：

kdAδdAjcosβ1+kdCδdCjcosβ2=0

(5)

由输出盘与等速钢球之间的相对位移关系，建立输出盘动力学微分方程：

(6)

式中，Tc输出轴转矩；k5y为y轴方向支承刚度。

1.4系统动力学微分方程

输入轴转速ωr与减速钢球转速ω2较小，将动力学微分方程中略去与ωr、ω2有关的项，并由式(1)～式(6)得简化后的动力学微分方程：

(7)

i=1,2,…，2Z2

M=diag[M0,M1,M2,M3,M4,M5]

M0=diag(m0,m0,J0)M1=(m1,m1,J1)

M3=diag(m3,m3,J3)M5=diag(m5,J5)

A1=

K11=k01x+k03xK22=k01y+k03y

A2=

K4xi=-(kC+kD)cos2βsinΦ3isinΦ4i

K4yi=(kC+kD)cos2βsinΦ3icosΦ4i

K5xi=(kC+kD)cos2βcosΦ3isinΦ4i

K5yi=-(kC+kD)cos2βcosΦ3icosΦ4i

K6xi=-(kC+kD)Z3ecos2βsinΦ3isinΦ4i

K6yi=(kC+kD)Z3ecos2βsinΦ3icosΦ4i

i=1，2，…，Z2

A4=diag[K1,K2,…,KZ2]

K7xi=(kA+kB+kC+kD)(cosβsinΦ4i)2

K7yi=-(kA+kB+kC+kD)cos2βsinΦ4icosΦ4i

K8yi=(kA+kB+kC+kD)(cosβcosΦ4i)2

K(2i+5)7=-(kA+kB)cos2βsinΦ4isinΦ3i

K(2i+5)8=(kA+kB)cos2βsinΦ4icosΦ3i

K(2i+5)9=-Z3e(kA+kB)cos2βsinΦ4isinΦ3i

K(2i+6)7=(kA+kB)cos2βsinΦ3icosΦ4i

K(2i+6)8=-(kA+kB)cos2βcosΦ3icosΦ4i

K(2i+6)9=Z3e(kA+kB)cos2βcosΦ4isinΦ3i

t=1,2,…,Z4

A81=diag(K411,K422,…,K4Z4Z4)

K4jj=(kdA+kdD)cos2β1+(kdB+kdC)cos2β2

Kyj=-(kdDcos2β1+kdCcos2β2)

K4uj=-(kdDcos2β1+kdCcos2β2)Rwsinφj

j=1,2,…,Z4

式中，M2为元素是m2的2Z2阶对角阵；M4为元素是m4的Z4阶对角阵。

刚度矩阵K为11+2Z2+Z4维的对称阵，q为系统的广义坐标列阵，质量矩阵M为对角阵。

动力学方程对应的特征方程为

(8)

h=x0,y0,u0,x1,y1,u1,x21,y21,x22,y22,…,x2(Z2-1),y2(Z2-1),x2Z2,y2Z2,x3,y3,u3,x41,y41,x42,y42,…,x4(Z4-1),y4(Z4-1),x4Z4,y4Z4,y5,u5

式中，ωh为系统h阶固有频率；φh为阵型矢量。

2固有特性分析

2.1结果求解与分析

动力学微分方程中的刚度系数如下：kA=8.15×106N/m，kB=8.73×106N/m，kC=kD=kdA=kdD=7.90×106N/m，kdB=kdC=1.90×106N/m，k01x=k01y=k1x=k1y=k5y=6×107N/m，k03x=k03y=7×107N/m，k1u=6×105N·m/rad。样机参数取值参见表1。

表1　计算参数

将刚度系数与表1中的参数代入式(8)，求得各阶固有频率，将各阶固有频率代入式(8)，获得模态振型坐标。将获得的固有频率从小到大依次排列，设为ω1～ω17，各阶固有频率如表2所示，表中，M为重根数。机构减速啮合副与等速啮合副部分振动模态分别如图4、图5所示。

表2　固有频率

由表2及模态振型可以得到如下规律：

(1)由表2可知，自由振动固有频率总数为37，由1个固有频率为0的11重根、1个固有频率为33 679 rad/s的4重根、1个固有频率为49 176 rad/s的8重根、14个单根组成，固有频率为0的重根个数与输入轴、中心盘、行星盘及输出轴的自由度个数相等。

(2)自由振动主要为三种模态：系统全振动模态、输出轴静止振动模态、输出轴扭转振动模态。输出轴静止振动模态可分为减速钢球平移振动、等速钢球直线振动与等速钢球静止振动。减速钢球平移振动与等速钢球直线振动对应的固有频率均存在重根，重根数分别为8和4。

(3)每个单根固有频率对应一种振型。在系统全振动模态对应的振型中，输入轴、中心盘、行星盘与输出轴均存在平移和扭转振动，减速钢球为平移振动，等速钢球为直线振动。

(4)输出轴扭转振动中，输出轴无直线振动；输入轴扭转振动中，输入轴无平移振动。

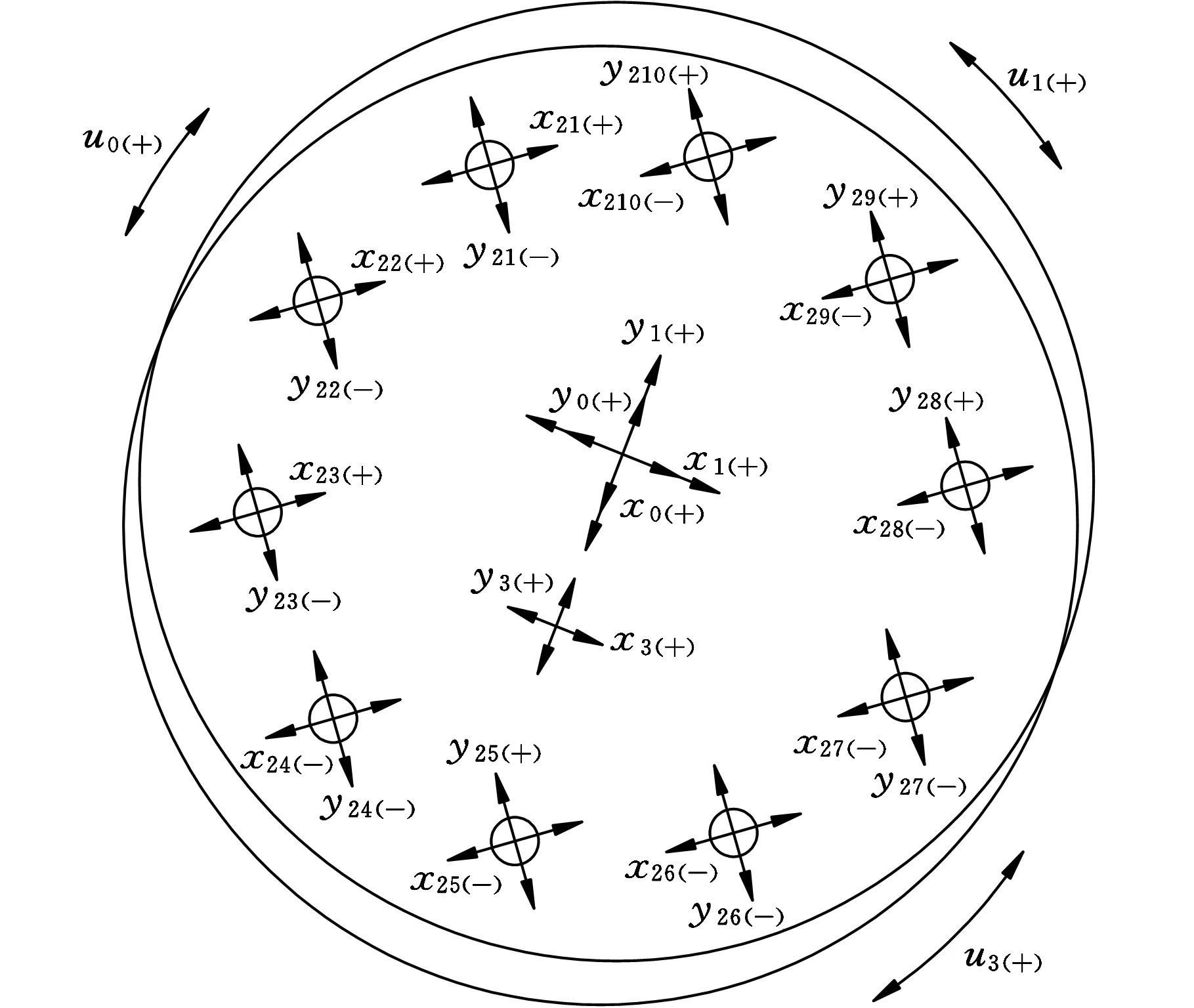
(a)ω3=13 843 rad/s

(b)ω14=65 477 rad/s

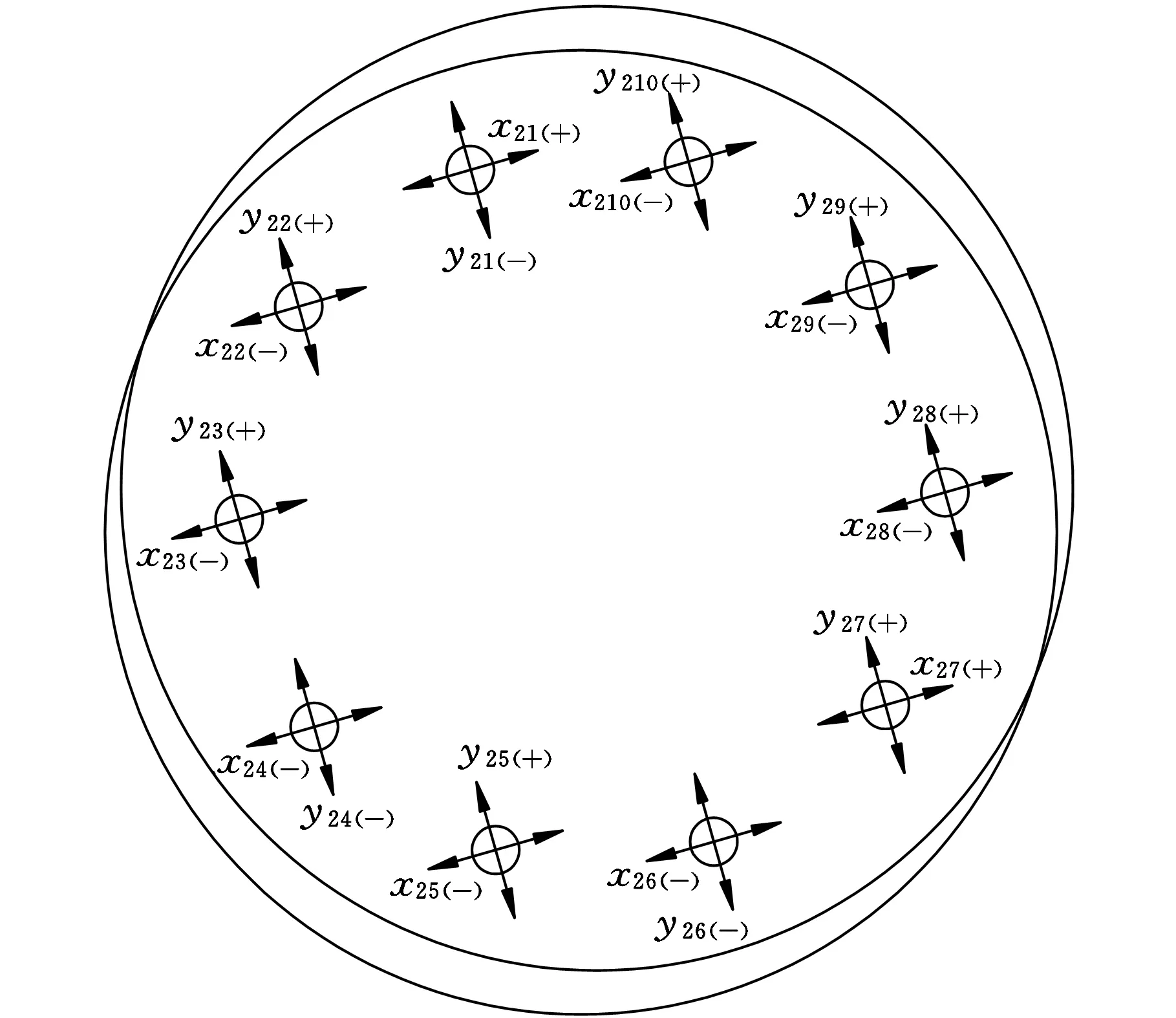
(c)ω6=33 679 rad/s图4　减速啮合副模态振型

(a)ω3=13 843 rad/s

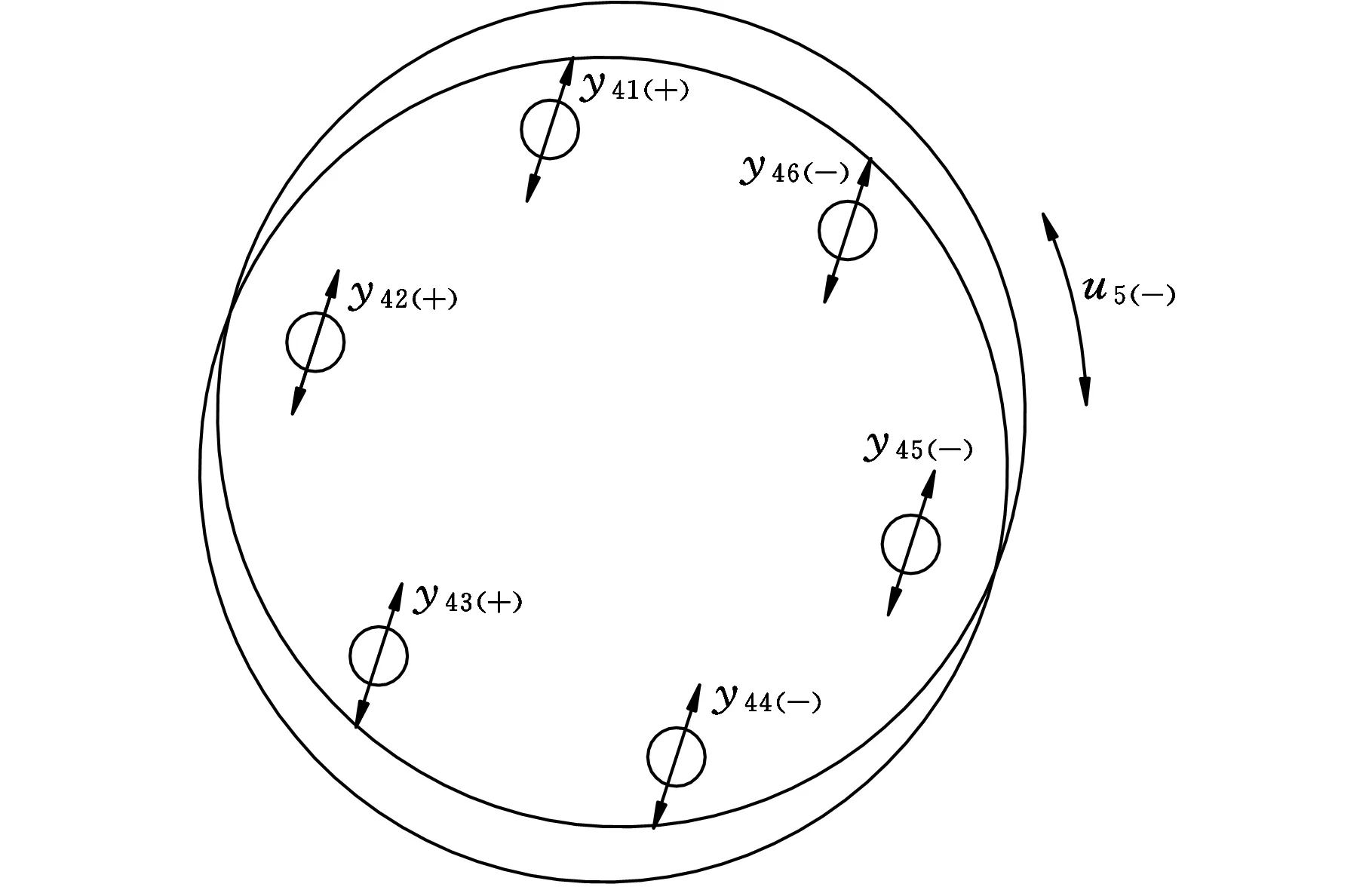
(b)ω14=65 477 rad/s

(c)ω12=49 176 rad/s 图5　等速啮合副模态振型

(5)减速钢球平移振动模态中，只存在减速钢球平移振动；等速钢球直线振动中，只存在等速钢球直线振动；等速钢球静止振动模态中，等速钢球无振动。

将文献[6]中所建模型称为简化模型，在该模型基础上求解得到的固有频率阶数较少且均为单根，仅存在系统全振动模态。该简化模型与新模型相比，固有频率与主振型的研究结果存在较大差异。

2.2参数对固有频率的影响分析

改变系统部分参数值，分析参数变化对系统固有频率的影响。对参数进行分析时，选取短幅系数K、滚圆半径r0、行星盘支撑刚度系数k03x和k03y为自变量，通过数值计算得到固有频率随参数变化的曲线。选取系统全振动模态与输出轴扭转振动模态对应的固有频率进行分析。

系统全振动模态固有频率变化如图6所示。固有频率ω3与ω4随K、r0的增大而增加。r0>4 mm时，ω3曲线斜率发生较大变化；r0>5 mm时，ω4曲线斜率发生较大变化。k03x对ω3与k03y对ω4产生较小影响，k03x对ω4及k03y对ω3不产生影响。

图6　参数对ω3与ω4的影响

输出轴扭转振动模态固有频率变化如图7所示。ω13随K、r0、k03x增加而增大，ω14随K、k03x增加而增大。r0增加时，ω14先减小后增加，存在最小值。k03y<3×107N/m时，ω14随k03y增大而增大；k03y=3×107N/m时，发生模态跃迁；k03y>3×107N/m时，ω14为定值。

图7　参数对ω13与ω14的影响

减速钢球数目变化时，系统固有频率单根数与ω6重根数不发生变化，ω1与ω12重根数发生变化(变化量均与Z2变化量相同) 。如图8所示，ω3、ω4与ω13随Z2增加而增大，ω14随Z2增加而减小。

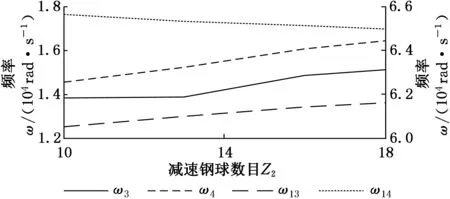
图8　Z2对固有频率的影响

短幅系数K与支承刚度变大，有助于提高系统的固有频率，使系统远离振动频率产生的影响；r0与Z2的变化对固有频率的影响具有不确定性；支承刚度变化时，固有频率会出现模态跃迁，工程设计应避开此类参数敏感点。传动比i与减速钢球数Z2之间的关系为i=(Z2+1)/2，则不同传动比对摆线钢球行星传动固有频率的影响具有不确定性。

将简化模型与新模型研究结果进行对比可知，同一参数的变化对不同模型中固有频率产生的影响不同。简化模型中，支承刚度、传动比与偏心距均主要影响高阶固有频率，固有频率值随参数值增加而变大。

3样机试验

在大多数情况下，系统的基频稳态响应占据主导地位，工程实际中最关注系统的基频稳态响应[11]。因此，采用SZCJ锤击法振动测试系统对摆线钢球行星传动系统固有频率进行测试，采样频率为20 kHz。本实验采用京仪北方测振分公司LC-1型力锤、BZ1124-103加速度传感器、DHF-8型多通道电荷放大器和LMS Test．Lab9A版数据分析软件。

对传动机构进行悬挂测试，测点为输出端面(间隙调解机构处)，采用固定响应点、移动敲击点的测试方法，选取外壳表面圆柱面和行星盘端面为激励点。测试过程中得到的每一条曲线均为单次敲击所测试的结果，振动测试曲线如图9所示，线频率对比如表3所示。角频率ωi(rad/s)与线频率fi(Hz)之间的转换关系为fi=ωi/(2π)。

由于只在一点敲击(激励)，敲击能量分布不均匀，因此测试结果中均在较高阶固有频率处出现了“漏频”现象。对比表3中固有频率的测试值与理论计算值可知，敲击大圆柱面中间敲击点时，“漏频”现象出现在固有频率f10处，绝对误差最大值530 Hz出现在f13处，其余误差相对较小；敲击小圆柱面中间敲击点时，“漏频”现象出现在固有频率f12处，绝对误差最大值446 Hz出现在f13处，相对误差最大值7.3%出现在f4处，其余误差相对较小；敲击中心盘端面敲击点时，“漏频”现象出现在固有频率f9、f10和f12处，相对误差最大值7.5%出现在f2处，其余误差相对较小。在对机构不同点进行敲击时，固有频率理论计算结果与测试结果之间误差较小，从而验证理论推导的正确性。

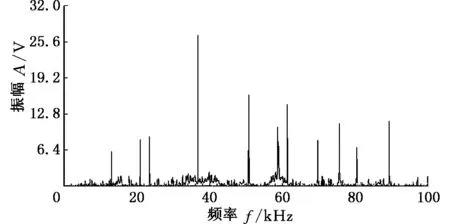
(a)大圆柱面中间敲击点

(b)小圆柱面中间敲击点

(c)中心盘端面敲击点图9　振动测试频率曲线

Hz

4结论

(1)在摆线钢球行星传动平移-扭转耦合动力学模型基础上建立的动力学微分方程能够较全面地揭示摆线钢球行星传动的固有特性，自由振动除有系统全振动模态之外，还有输出轴静止振动模态、输出轴扭转振动模态。

(2)减速钢球数变化时，固有频率单根数目不发生变化，部分重根数增加，传动比变化对固有频率的影响具有不确定性，输出轴支承刚度变化对固有频率产生较大影响。

(3)对摆线钢球行星传动不同点进行敲击时得到的试验结果之间存在较小误差，固有频率理论计算结果与测试结果之间存在较小误差，验证了考虑活齿及啮合副无隙啮合的平移-扭转耦合动力学模型理论推导的正确性。

参考文献：

[1]王国彪，赖一楠，范大鹏，等. 新型精密传动机构设计与制造综述[J]. 中国机械工程，2010 ，21(16)：1891-1897.

WangGuobiao,LaiYinan,FanDapeng,etal.SummaryofNewTypePrecisionTransmissionDesignandManufacture[J].ChinaMechanicalEngineering, 2010, 21(16):1891-1897.

[2]徐盛林，陈耿. 精密超精密定位技术及其应用[J]. 中国机械工程，1997，8(4)；73-75.

XuShenglin,ChenGeng.PrecisionUltra-precisionPositioningTechnologyandItsApplications[J].ChinaMechanicalEngineering, 1997,8(4):73-75.

[3]寺田英嗣, 牧野洋, 今瀬憲司. サイクロイドボール減速機の基礎解析[J]. 精密工学会誌，1995，61(12)：1075-1079.

[4]TeradaH.TheDevelopmentofGearlessReducerswithRollingBalls[J].JournalofMechanicalScienceandTechnology, 2010, 24(1):184-195.

[5]张鹏，安子军，杨作梅. 摆线钢球行星传动啮合副非线性力学性能研究[J]. 工程力学，2010，27(3)：186-192.

ZhangPeng,AnZijun,YangZuomei.ResearchonNonlinearMechanicalPropertiesforEngagementPairofCycloidBallPlanetaryTransmission[J].EngineeringMechanics, 2010, 27(3):186-192.

[6]张鹏，安子军. 摆线钢球行星传动动力学建模与固有特性分析[J]. 中国机械工程，2014，25(2)：157-162.

ZhangPeng,AnZijun.DynamicsModelandNaturalCharacteristicsofCycloidBallPlanetaryTransmission[J].ChinaMechanicalEngineering, 2014, 25(2):157-162.

[7]梁尚明，张均富，徐礼柜，等. 摆动活齿传动系统振动的动力学模型[J]. 振动工程学报，2003，13(3)：285-289.

LiangShangming,ZhangJunfu,XuLiju,etal.DynamicModelofSwingMovableTeethTransmissionSystemVibration[J].JournalofVibrationEngineering, 2003, 13(3):285-289.

[8]梁尚明, 张均富, 徐礼拒. 摆动活齿传动系统的弹性动力学模型的研究[J]. 机械工程学报，2002，38(S)：142-146.

LiangShangming,ZhangJunfu,XuLiju.StudyonElasto-dynamicModelofSwingMovableTeethTransmissionSystem[J].ChineseJournalofMechanicalEngineering, 2002, 38(S):142-146.

[9]李冲, 许立忠, 邢继春. 压电谐波传动系统活齿传动自由振动分析[J]. 中国机械工程,2015，26(1):12-17.

LiChong,XuLizhong,XingJichun.FreeVibrationofOscillatingToothDriveforanElectromechanicalIntegratedHarmonicYiezodriveSystem[J].ChinaMechanicalEngineering, 2015, 26(1):12-17.

[10]XuLizhong,ZhuXuejun.NaturalFrequenciesandVibratingModesforaMagneticPlanetaryGearDrive[J].ShockandVibration, 2012, 19(6):1385-1401.

[11]刘振皓，巫世晶，王晓笋，等. 基于增量谐波平衡法的复合行星齿轮传动系统非线性动力学[J].振动与冲击，2012，31(3)：117-122.

LiuZhenhao,WuShijing,FangXiaosun,etal.NonlinearDynamicsofCompoundPlanetaryGearSetsBasedIncrementalHarmonicBalanceMethod[J].JournalofVibrationandShock, 2012, 31(3):117-122.

(编辑张洋)

收稿日期：2015-09-21

基金项目：国家自然科学基金资助项目(51275440)；河北省自然科学基金资助项目(E2013203085)

中图分类号：TH113.1

DOI：10.3969/j.issn.1004-132X.2016.14.008

作者简介：杨荣刚，男，1988年生。燕山大学机械工程学院博士研究生。主要研究方向为精密机械传动理论与应用。发表论文3篇。安子军(通信作者)，男，1960年生。燕山大学机械工程学院教授、博士研究生导师。段丽英，女，1982年生。燕山大学机械工程学院博士研究生。

Analysis of Free Vibration of Cycloid Ball Planetary Transmission

Yang RonggangAn ZijunDuan Liying

Yanshan University，Qinhuangdao，Hebei，066004

Abstract:In order to reveal the inherent characteristics of cycloid ball planetary transmission accurately, a translational-torsional coupling dynamics model of precision ball transmission was proposed. The relative displacement amount of each component was solved with load. Dynamics of differential equations were deduced, free vibration characteristic equation was given, and the natural frequency and principal modes were obtained. The impacts on the natural frequency of structure parameters was analyzed. Theoretical research was carried out to prove the experiments. The results show that: the mechanism has system-wide vibration mode, the output shaft stationary vibration mode and the output shaft torsional vibration mode; the influence of transmission ratio on natural frequency is uncertain; the output shaft bearing stiffness is a very important parameter of natural frequency that affects the natural frequency; and the correctness of theoretical deduction is verified by experiments.

Key words:cycloid ball planetary transmission; free vibration; four point engagement; modal analysis; axial preload