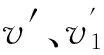微小尺度下平板间气体流动机理及压力特性分析

宁方伟　龙　威　刘　岩

昆明理工大学，昆明，650500



微小尺度下平板间气体流动机理及压力特性分析

宁方伟龙威刘岩

昆明理工大学，昆明，650500

摘要：基于平板间气膜内气体分子运动和碰撞的规律，提出气膜分层理论，将板间气膜内的气体划分为近壁层、稀薄层、连续流层。给出了划分稀薄层和连续流层的依据，建立分层物理模型并提出每层的控制方程，验证了分层理论的合理性。通过大规模原子/分子大型并行模拟器仿真板间气膜内气体流态并计算沿高度方向的压力，得出了如下结论：随着板间气体流速的增大，板间气膜有效压力减小，连续流层的厚度增大，稀薄层的厚度减小；当气体流速到达一定值时，气膜内压力不再分层，速度滑移现象可以忽略。

关键词：微机电系统；微流体；速度滑移；Knudsen数；分子碰撞

0引言

MEMS技术的发展为微流体技术的研究创造了条件。近十几年来，微流体技术在MEMS领域内逐渐成为一个非常大的分支，取得了很大的进展。微流体装置及组件主要包括微泵、微阀、微通道、微喷、微传感器和微混合器等。在这些装置中，微小尺度平行平板间气体流动成为微流体中主要研究内容。

板间气流由于尺度微小，稀薄效应显著，在固体界面上产生速度滑移，进而导致整个气膜内气体流态发生变化[1]。速度边界滑移经历了边界无滑移条件假设[2-3]、线性滑移条件假设、近似滑移本构方程的发展[4-5]。无滑移边界条件在微尺度流动分析中不再适用。Kn数(气体平均自由程与流场特征长度的比值)为0.1是Navier-Stokes方程和一阶速度滑移边界条件的上限[6]。当Kn数增大到1，文献[7-8]中的二阶模型完全失效。通过拟合DSMC(directsimulationofMonteCarlo)速度分布数据得到滑移系数建立新的滑移模型[9]，这种方法对计算机性能要求高。现有理论存在着对于大Kn数模型失效、计算量大、无法指导工程应用等缺陷。为弥补传统速度滑移理论的不足，更有效地结合工程应用，本文根据板间气膜内气体实际流态，提出气膜分层理论，建立相关的物理模型，提出相应的控制方程。根据控制方程，求解相应的宏观量，为研究板间气膜气体流动机理提供理论指导。

1理论分析

如图1所示，本文假设平板边界均为光滑平面，对于气膜中的流动气体，根据气体流态的不同，将气流划分为三层：近壁层，即与平板边界相接触的区域；连续流层，即中心线穿过的气膜中间区域；稀薄层，即近壁层和连续流层之间的区域。

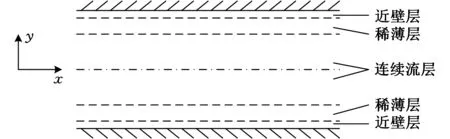
图1　板间气膜示意图

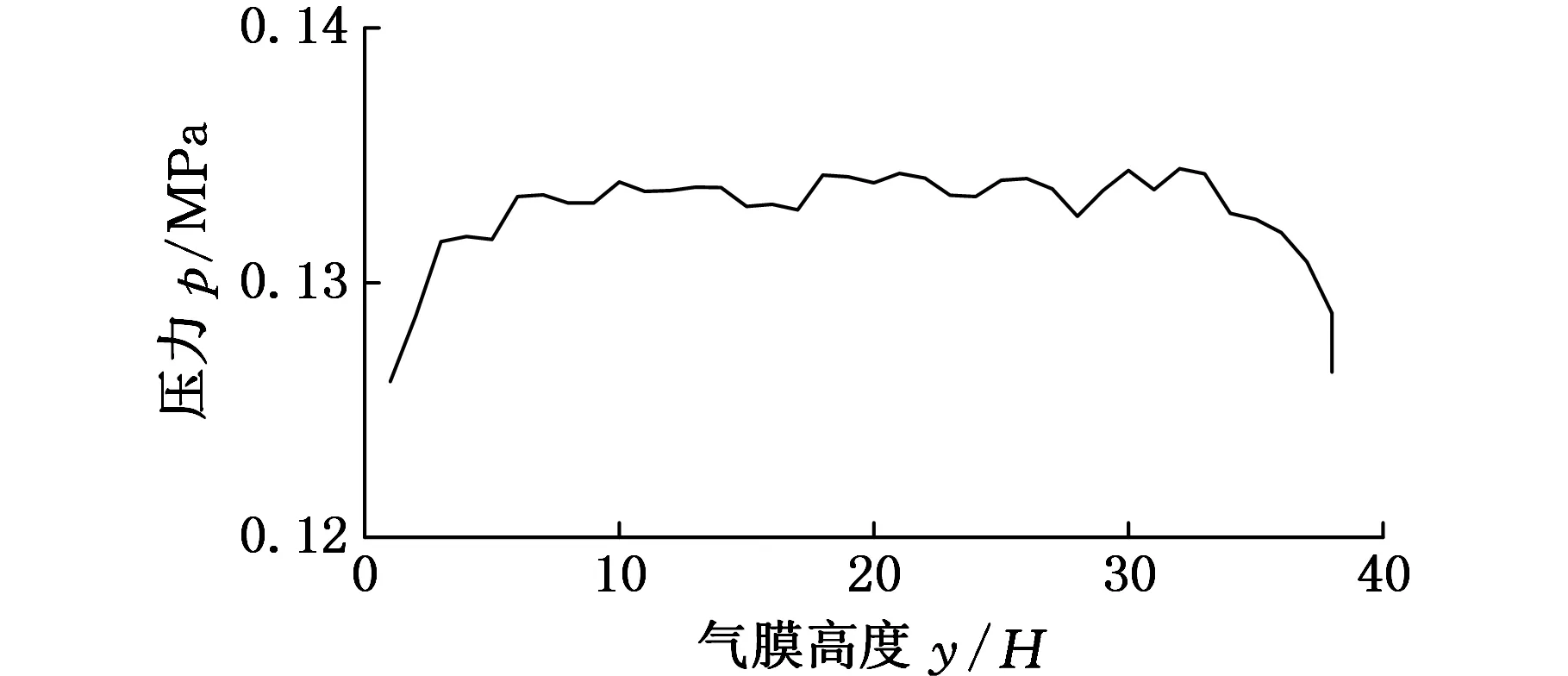
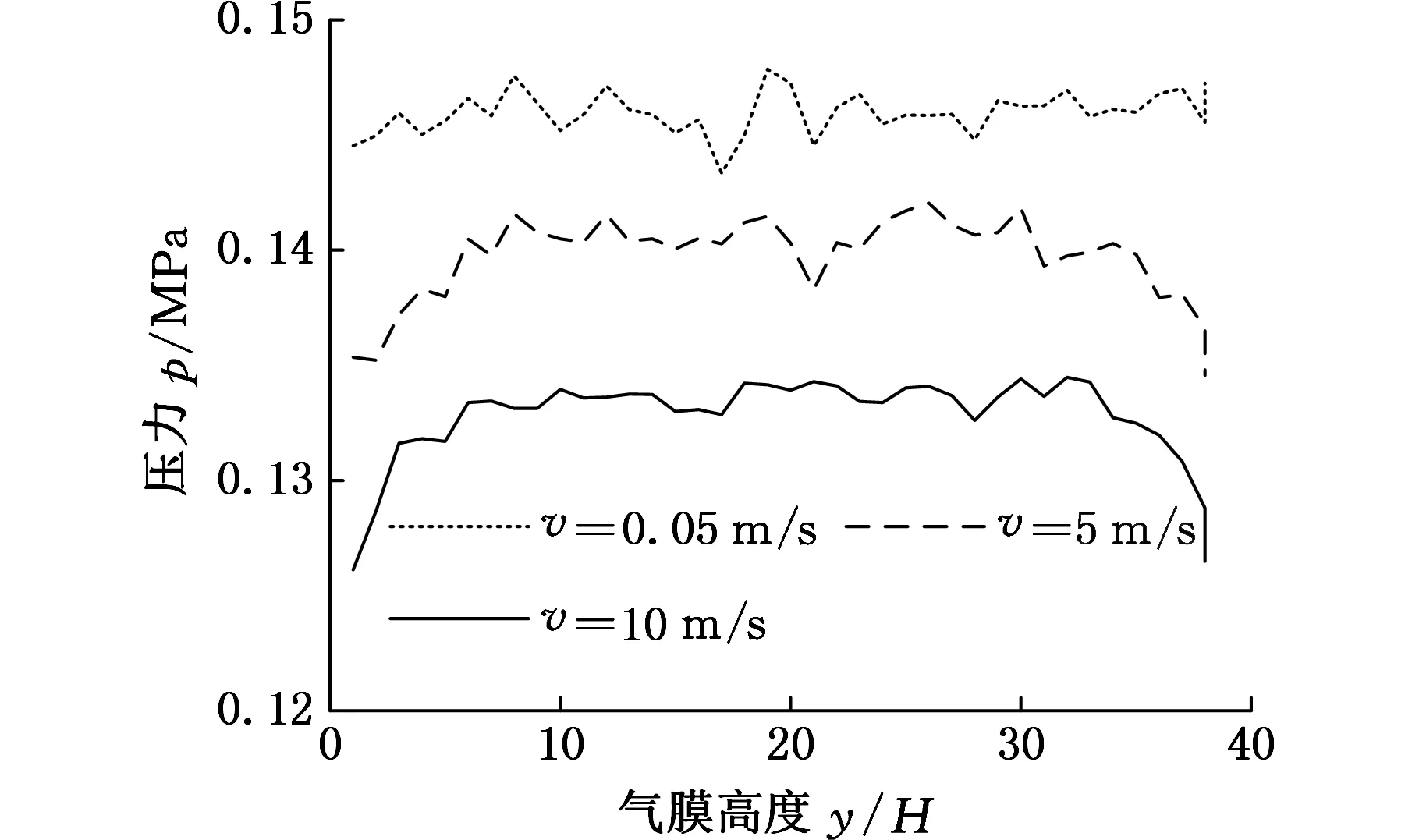
稀薄层中的气流为稀薄气体，气膜厚度为亚微米级，通过估算可得当地Kn*数在0.1～10之间，即气体分子处于过渡区[10]。流体在低雷诺数，即1

(1)

式中，Re为当地雷诺数；λ为分子平均自由程；L为流体特征长度；d为流场特征尺寸；υ为流体的运动黏度；c0为气体宏观运动速度。

Nfw=1为连续流层与稀薄层的分界线；Nfw>1时，当地气体属于连续流层；Nfw<1时，当地气体属于稀薄层。

1.1近壁层

近壁层的厚度为单位分子的平均自由程(工况下，一个气体分子在连续两次碰撞通过的平均距离)，该层内分子与壁面碰撞时按照完全漫反射的边界条件[11]。分别建立分子与固体壁面质量、法向动量与近壁层的关系：

c0=v0+vi

(2)

(3)

(4)

式中，φii(c)、φiiR(c)分别为i组元的质量和入射质量；φiw(c)为i组元的漫反射质量；vi为i组元分子漫发射运动速度；v0为定义量；y为物面法向坐标；fs为近壁层外缘速度分布函数；fw为壁面处Maxwell速度分布函数；下标s、w分别表示近壁层外缘和壁面量。

1.2稀薄层

本文采用变径硬球(variablehardsphere)模型，应用Boltzmann方程对其进行研究，即

(5)

f=f(r,v,t) f′=f(r,v′,t)

基于气体分子碰撞松弛特性，本文采用BGK模型方程，以一个简单的算子代替Boltzmann方程的碰撞项，其表达式(不考虑外力)可以写为

(6)

(7)

1.3连续流层

将这一层中的气流运动看成二维流动，在图1所示的坐标系下，忽略质量力，应用Stokes假设，即可得到相应的二维定常不可压缩Navier-Stokes方程：

(8)

(9)

式中，p为压力；ρ为气体密度；μ为气体动力黏性系数；U为流体质点速度沿X方向的分量；V为流体质点速度沿Y方向的分量。

二阶速度滑移条件：

(10)

2仿真计算

2.1气膜分层现象

利用LAMMPS(large-scaleatomic/molecularmassivelyparallelsimulator)对板间气膜内分子运动情况进行模拟，板间气膜高度h=40nm，Kn=1.5，入口气体流速v=10m/s，环境温度为室温。图2a中，折线表示气体分子在一定时间内的运动轨迹；图2b所示为气膜内气体分子在某一瞬间的分布。以下固体界面为起点，沿气膜高度方向每隔1nm测量每点的压力大小，可得气膜内垂直方向压力分布情况，如图2c所示。

(a)板间气膜内分子运动路径图

(b)板间气膜内分子分布示意图

(c)沿气膜高度方向压力分布图2　板间气膜分层区域仿真图

从图2a、图2b可以看出气膜内有分层现象，稀薄层和连续流层较为明显。稀薄层(0

2.2分层区域的范围

由图3可以看出，随着气体流动速度的增大，稀薄层的厚度减小，连续流层的厚度增加。气膜内稳定压力逐渐降低，同时在稀薄层出现明显的压力梯度。气体流速越大，稀薄层的压差越大，斜率越大，层厚越小。随着气体流速的减小，稀薄层逐渐淡化，压差越小，斜率越小，当气体流速降至0.05m/s以下时，稀薄层的压力基本上和连续流层的压力一致，不再呈现明显的压力变化，此时气膜内的速度滑移现象可以忽略。

(a)路径图v=0.05 m/s

(b)路径图v=5 m/s

(c)路径图v=10 m/s

(d)沿气膜高度方向压力分布图3　不同速度下板间气膜分层区域仿真图

2.3LAMMPS仿真与DSMC计算结果的比较

当气膜的长高比为100，Kn=1.5，量纲一气体流动速度(气体速度与声速之比)Ma=1，计算时，y/H=0表示下壁面位置，y/H=1表示上壁面位置，其中，H为上下壁面的距离。用LAMMPS和DSMC分别计算气膜沿高度方向的压力，如图4所示。从LAMMPS和DSMC计算结果来看，越靠近上下壁面，压力越小，并且出现明显的压力梯度，在支撑气膜中间区域，压力变化不明显。LAMMPS与DSMC计算结果相比较，数值计算结果相近，从LAMMPS仿真结果中还可明显看出气膜分层现象。

图4　LAMMPS和DSMC计算结果

3结论

(1)建立了平板间气膜的物理模型，提出了气膜分层理论，由LAMMPS流态仿真及压力计算可以看出，将板间气膜划分为近壁层、稀薄层、连续流层是有效的，速度滑移边界条件分层理论是可行的。

(2)板间气体流速增加时，气膜的有效压力减小；连续流层的厚度增大，稀薄层的厚度减小；稀薄层内的压差变大，压力梯度增大。板间气体流速减小时，气膜的有效压力增大；连续流层的厚度减小，稀薄层的厚度增大；稀薄层内的压差变小，压力梯度减小。

(3)LAMMPS计算仿真结果与DSMC计算相近，LAMMPS具有可靠性，进一步证明将将板间气膜划分为近壁层、稀薄层、连续流层是可行的。

参考文献：

[1]ZhouJianfeng,GuBoqin,ShaoChunlei.BoundaryVelocitySlipofPressureDrivenLiquidFlowinaMicronPipe[J].ChineseScienceBulletin, 2011,56:1603-1610.

[2]DeGennesPG.OnFluid/wallSlippage.//[M]SimpleViewonCondensedMattcr. 3ed.Singapore：WorldScicntificPublishing, 2003:351-353.

[3]LaugaE,BrennerMP,StoneHA.Microfluidics：TheNo-slipBoundaryCondition[M]//SpringerHandbookofExperimentalFluidMechanics.Berlin:Springer, 2007: 1219-1240.

[4]吴承伟,马国军,周平.流体流动的边界滑移问题研究进展[J].力学进展,2008,38(3) :265-281.

WuChengwei,MaGuojun,ZhouPing.ResearchProgressinBoundarySlipProblemsofFluidFlow[J].AdvancesinMechanics,2008,38(3) :265-281.

[5]赵亚溥.表面与界面物理力学[M].北京:科学出版社, 2012 :306-318.

[6]张忠强.流体在纳米微通道中的流动及传输特性研究[D].大连:大连理工大学,2010.

[7]谢翀,樊菁.Navier-Stokes方程二阶速度滑移边界条件的检验[J].力学学报,2007,39(1):1-6.

XieChong，FanJing，TheTestofSecondOrderVelocitySlipBoundaryConditioninNavier-StokesEquations[J].ChineseJournalofTheoreticalandAppliedMechanics,2007,39(1):1-6.

[8]刘加利,张继业,张卫华.基于格子Boltzmann方法的微气体流动速度滑移边界条件的检验[J].真空科学与技术学报,2013,33(7) :647-653.

LiuJiali，ZhangJiye，ZhangWeihua.TheTestofVelocitySlipBoundaryConditioninMicroGasFlowBasedonLatticeBoltzmannMethod[J].ChineseJournalofVacuumScienceandTechnology, 2013,33(7):647-653.

[9] 龙建清,陈冰冰,郑三龙，等.基于DSMC方法的微槽道流滑移系数研究[J].浙江工业大学学报,2010,38(4):392-395.

LongJianqing，ChenBingbing,ZhengSanlong，etal.SlipCoefficientofMicroChannelFlowsBasedonDSMCMethod[J].JournalofZhejiangUniversityofTechnology, 2010，38(4):392-395.

[10]樊菁.稀薄气体动力学:进展与应用[J].力学进展,2013,43(2):185-201.

FanJing.RarefiedGasDynamics:AdvancesandApplications[J]AdvancesinMechanics, 2013,43 (2): 185-201.

[11]张海军,祝长生,杨琴,等.广义Maxwell速度滑移边界模型[J].中国科学:物理学力学天文学,2013,43(5):662-669.

ZhangHaijun，ZhuChangsheng，YangQin,etal.GeneralizedMaxwellVelocitySlipBoundaryModel[J].ScientiaSinica:Physica,Mechanica&Astronomica, 2013,43(5):662-669.

(编辑张洋)

收稿日期：2015-09-24

基金项目：国家自然科学基金资助项目(51305185)

中图分类号:TH47

DOI：10.3969/j.issn.1004-132X.2016.14.004

作者简介：宁方伟，男，1991年生。昆明理工大学机电工程学院硕士研究生。主要研究方向为静压润滑。发表论文4篇。龙威(通信作者)，女，1981年生。昆明理工大学机电工程学院副教授。刘岩，男，1989年生。昆明理工大学机电工程学院硕士研究生。

Analysis of Gas Flow Mechanism and Pressure Characteristics between Plates in Micro Scale

Ning FangweiLong WeiLiu Yan

Kunming University of Science and Technology,Kunming,650500

Abstract:Stratification theory of the gas film was proposed herein, which was based on molecular motion and collision law of the gas in the film between plates. The film was divided into near wall layer, thin layer, continuous flow layer. And the basis for dividing thin layer and continuous flow layer was also given, in addition, physical model and its corresponding equations were proposed. Flow patterns and pressure distribution in the height direction were simulated and calculated by LAMMPS(large-scale atomic/molecular massively parallel simulator). It is concluded that with increasing gas flow rate, the pressure of gas film is decreased, continuous flow layer thickness is increased, the thickness of the thin layer is decreased. There is no layered pressure in the gas film anymore, velocity slippage may be ignored.

Key words:micro-electro-mechanical system(MEMS); microfluidics; velocity slip; Knudsen number; molecular collision