套期保值比率模型的比较选择研究——基于沪深300指数的分析

黄文彬　郑丽娟　林银瑞

(福州大学经济与管理学院， 福建福州　360116)



套期保值比率模型的比较选择研究
——基于沪深300指数的分析

黄文彬郑丽娟林银瑞

(福州大学经济与管理学院， 福建福州360116)

摘要：以沪深300股指期货4种合约的日频率和15分钟、10分钟、5分钟、1分钟频率的高频数据为对象，检验在1种低频数据和4种高频数据环境下，静态的OLS模型、B-VAR模型、ECM模型和动态的Diagnoal-BEKK模型、CCC-GARCH模型、Diagnoal-VECH模型、DCC-GARCH模型的套期保值绩效，从而选择最优套保模型以及最优的套期保值数据频率类型。实证结果表明：套期保值绩效随着数据频率的提高而降低，日数据是最优套期保值数据频率类型。在日数据下，当月期货合约的最优套保模型为OLS模型，其他三种合约的最优套保模型为CCC-GARCH模型。在日数据下，下月期货合约的套期保值效果最优。

关键词：套期保值; 沪深300; 不同频率; GARCH模型

一、引言

我国期货市场经历了理论研究、试点、发展三个阶段，明确了期货市场具有分散转移风险、保值和预期价格等功能，期货具有风险大、变化快的特点。[1]相比英、美等国的成熟资本市场，我国期货市场存在较大的系统风险。有资料显示，我国股市的平均市场性风险高达40%。[2]

自从我国第一只股指期货——沪深300股指期货合约2010年4月16日在中国金融期货交易所上市后，股指期货市场交易十分活跃。至2014年10月，总成交5.29亿手，总成交金额391.5万亿元，日均成交48.79万手，日均成交金额3606亿元。仅从单个产品的交易量来看，沪深300股指期货已经成为全球第四大股指期货产品。沪深300股指期货与现货高度拟合，价格相关性高达99.9%，收益率相关性也达到94.5%。[3]随着股指期货的上市，我国股市波动率显著降低，沪深300指数在股指期货上市后波动率下降了40%，涨跌幅超过2%的天数下降了59%。沪深300股指期货已经成为我国各类投资者最重要的交易工具之一。投资者利用沪深300股指期货进行套保保值和风险管理将是大势所趋，以基金、保险机构为代表的各类机构投资者和风险管理者更是充分利用沪深300股指期货规避和化解股票市场的系统性风险。

影响套期保值的因素很多，包括交易成本，现货和期货价格间的协整关系、两者间的非线性关系，是否考虑套期保值后的收益情况，是否区分套期保值的买卖方向等。目前套期保值比率研究包括0LS模型、基差逐利套保模型、B-VAR模型、ECM模型等静态模型，以及ARCH模型、GARCH模型等动态模型。除了以上模型外，研究中还运用了一些新方法，包括展期(多期)套期保值法 、下偏矩风险法 、支持向量机(SVM)模型 、岭回归模型 、VecHAR-RVRCOV-J模型 ，以及Copula函数的利用、蒙特卡罗模拟、随机Lagrange方法等。[4][5][6][7][8][9]

针对最优套期保值比率模型，国内外均进行了大量的研究。套期保值比率的计算最早通常是采用静态比率，如普通最小二乘法(OLS)、向量自回归模型(VAR)、向量误差修正模型(VECM)等。早期国外学者如Ederington，Figlewski，Lee等和Benet都证实这3种静态套保模型具有较好的避险效率。[10][11][12][13]但是随着时间序列理论的发展，特别是多变量的条件波动率模型——多元广义自回归条件异方差模型MVGARCH的出现，静态套保比率的方法被认为存在许多缺点。Cecchetti等，Baillie和Myers，Myers，Kroner和Sultan，Park和Switzer以及Choudhry的研究都说明运用MVGARCH模型分析现货和期货间的条件波动率以及条件相关系数，可以更好地构建动态的避险比率获得更好的避险效果。[14][15][16][17][18][19]Lien及付剑茹和张宗成则认为动态套保策略仍存在异议。[20][21]

我国这样一个新兴的金融市场，沪深300股指期货在推出四年后，它的避险效果到底如何呢？是静态套保模型有效还是动态套保模型有效呢？随着网络信息技术的快速发展、高频交易的兴起，金融机构往往也需要在高频环境下即时调整资产的头寸，低频环境下的股指期货套期保值与高频环境下的股指期货套期保值存不存差异？这些问题的研究具有重要的现实意义。本文针对四种不同到期期限的沪深300指数期货合约，利用低频的日数据和最为常见的4种高频数据，基于3种静态模型包括OLS模型、B-VAR模型、ECM模型和4种动态模型包括Diagnoal-BEKK模型、CCC-GARCH模型、Diagnoal-VECH模型、DCC-GARCH模型,对不同期限、不同频率、不同模型的避险效果作较为全面的分析。

二、套保模型和方法

套期保值是指企业为规避商品价格风险、汇率风险、股票价格风险、信用风险等，指定一种或一种以上的套期工具，使套期工具的公允价值或现金流量变动，抵消预期的被套期保值项目全部或部分公允价值或现金流量变动。[22]套期保值的交易原则包括4个，具体是：品种相同或相近原则、月份相同或相近原则、方向相反原则、数量相当原则。

套保理论的发展主要经历了三个阶段，第一阶段为传统的套期保值理论，该理论认为最优套期保值比率为1，即1单位的现货可以用1单位的期货来规避风险[23]；第二阶段为基差逐利型套期保值理论，该理论认为套期保值的核心在于通过观察基差、预测基差变化，而不是通过消除价格波动风险，从而获取最大利润[24]；第三阶段是现代套期保值理论。[25]在现代套期保值理论的研究中，许多学者主要是从如何最小化组合收益风险的角度研究期货市场最小风险套期保值比率，并将最优套期保值比率分为静态套期保值比率和动态套期保值比率。

本文采用的套期保值模型也是基于风险最小化的角度。实证模型包括普通最小二乘法模型(OLS)、二元向量自回归模型(B-VAR)、误差修正模型(ECM)、Diagonal-BEKK(1，1)模型、DVECH-GARCH模型、CCC-GARCH模型、DCC-GARCH模型。

(一)套期保值比率定义

(1)

(2)

(3)

1. 静态套期保值比率法

(1)OLS模型

采用普通最小二乘法，假设估计的模型如下：

(4)

(2)B-VAR模型

考虑普通最小二乘法可以很快得到最优套期保值比率，但是OLS法是根据无条件分布估算的套保比率，而且若回归方程存在残差自相关，估计的回归方程会有偏差。利用向量自回归模型，通过选择合适的滞后阶数，可以解决残差自相关问题。故从理论上的无偏性来说，若回归方程存在残差自相关现象，VAR模型优于OLS模型。本文考虑期货和现货这两个变量之间的关系，利用的是二元向量自回归模型(B-VAR)，模型如下：

(5)

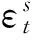
在该模型下，最优套保比率为

(6)

(3)ECM模型

B-VAR模型考虑了滞后期收益率的影响，但若期货与现货价格之间存在协整关系，忽略这种关系估计的最优套期保值比率可能会比实际值偏小。为了进一步提高模型的精度，考虑协整关系，利用误差修正模型进行估计。

为了减少波动的影响，首先对现货和期货取自然对数，并对其进行平稳性检验。若现货和期货价格自然对数序列为不平稳序列，对其取一阶差分，获得对数收益率序列，再对对数收益率序列进行平稳性检验；若其为平稳序列则说明现货和期货自然对数序列之间存在协整关系，且为一阶单整，此时，可以建立现货和期货对数收益率的误差修正模型。

误差修正模型的一般形式如下：

(7)

其中:Zt-1为误差修正项，在误差修正模型下估计的最优套期保值比率为

(8)

2. 动态套期保值比率法

(1)Diagonal-BEKK(1，1)模型

OLS模型、B-VAR模型、ECM模型都是静态模型，即最优套保比率不随时间变动而变动，它不符合现实金融市场时变的特点。因此，从理论上说，动态套期保值模型更能准确估计出时变最优套保比率。目前在动态套期保值比率研究方面，GARCH相关模型已有了较多的理论成果。本文利用Diagonal-BEKK(1，1)法来估计最优套期保值比率。

BEKK(1，1，1)模型如下：

rt=μ+εt

(9)

其中:rt=(rs,t,rf,t)′是现货收益率和期货收益率组成的向量，C为二阶上三角矩阵，A和B为二阶的参数矩阵。

Ht可以展开为如下形式：

(10)

上面的矩阵方程式就是完全BEKK模型。

(2)CCC-GARCH模型

该模型假设不同资产收益率之间的相关关系不会随时间改变，为一个固定的常数，假定恒定条件下的相关系数矩阵如下式：

(11)

方差-协方差结构矩阵如下：

(12)

(13)

(3)Diagonal- VECH模型

多变量向量误差条件异方差模型VECH(p，q)的一般形式为：

(14)其中:Ai(i=0,1,…p)和B(j=1,2,…,q)均为N*N的对称系数矩阵；算子⊗为Hadamard乘积，表示矩阵的对应元素相乘。

最一般的情形是不对系数矩阵再施加任何的限制，每个矩阵都包含N(N+1)/2个参数，这很难保证条件协方差阵是正定的。将A0以外的所有系数矩阵限定为对角阵，得到的模型也被称作DVEC(p，q)模型，此时，Ai(i=0,1,…,p)和B(j=1,2,…,q)均为下三角阵。[26]

(4)DCC-GARCH模型

对于Diagonal-BEKK模型而言，由于它对不同市场之间的波动传达效应缺乏考虑，对于CCC-GARCH模型而言，它的假设前提是各个时间序列之间的相关系数为固定不变的一个常数，这些都不符合现实的经济特征。而DCC-GARCH模型考虑了动态模型的相关系数，同时又比BEKK-GARCH模型更好地描述了不同时间序列之间的波动传递。[27]从这些理论方面来看，DCC-GARCH模型在估计动态套期保值比率方面更有优势。此外，DCC-GARCH模型在计算方面具有较好的优势，较大规模的相关系数矩阵可以用它来进行估计，因此，它可以对多个时间序列的波动情况进行较好的研究。

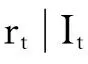
Ht= DtRtDt

Rt= (Q*)-1Qt(Q*)-1

(15)

DCC-GARCH模型可以通过两步骤来估计，首先估计每一资产的单变量GARCH过程，然后通过获得的条件方差标准化残差估计动态相关结构的参数，具体的模型参数估计利用R软件进行估计。

因为收益率存在尖峰厚尾特点，学生t分布更能反映收益率的这个特征，所以4种动态模型在模型设定上，模型的误差项分布均采用多元学生t分布。

(二)套期保值绩效的衡量指标

本文采用的套期保值方法是在方差最小的情况下进行的，目前针对这种方法下的套期保值效果检验主要是估算方差减小的程度，即进行套期保值的组合的方差比未进行套保的现货的方差的减小程度，计算公式如下：

(16)

三、实证结果

(一)样本数据及采用的软件说明

本部分选取沪深300指数(hs300)、沪深300股指期货当月合约(ifl0)、下月合约(ifl1)、下季合约(ifl2)、隔季合约(ifl3)这5个合约的日收盘价、15分钟收盘价、10分钟收盘价、5分钟收盘价、1分钟收盘价。样本期间为2013年1月4日至2014年12月31日，数据来源于通达信数据库，利用Eviews 7.2和R软件对相关模型进行估计。

现货收益率和4种不同到期期限股指期货收益率序列在样本内的基本统计特征列于表1中。对于日数据、15分钟数据、10分钟数据、5分钟数据以及1分钟数据这五种频率数据，从平均收益率来看，样本期间现货收益率和期货收益率的平均值差别不大；从标准差来看，现货收益率的标准差最小，而期货收益率的标准差较大；从偏度来看，偏度值基本都小于零稍微左偏；从峰度值来看，4种不同到期期限的期货收益率的峰度值基本都等于现货收益率的峰度值，期货收益率比现货收益率具有更强烈的尖峰肥尾特征；从J-B统计量来看，现货收益率和4种不同到期期限的期货收益率的J-B统计量在5%的显著性水平下都显著不为0，说明沪深300指数以及4种不同到期期限的期货收益率均不服从正态分布，而且具有一般金融时序数据所特有的尖峰肥尾特征，4种不同到期期限的期货收益率的J-B统计量也明显大于现货收益率的J-B统计量，说明期货的波动性大于现货，这可能是因为期货交易成本相对较小，交易较为频繁，从而使得其市场波动性也较大；从单位根检验的ADF统计量来看，所有收益率的ADF统计量在5%的显著性水平下拒绝存在单位根的原假设，说明沪深300指数以及4种不同到期期限的期货收益率均是平稳的时间序列。

表1　期现货收益率的描述统计量和平稳性检验

(二)最优套期保值比率对比

汇总沪深300股指期货在不同频率、不同模型下的最优套期保值比率，结果如表2所示。

根据表2 数据可知：

(1)除了ifl3在DCC-GARCH模型下的套保比率外，同一期货合约在相同套期保值模型、不同数据频率下，它的套期保值比率不同，并且套期保值比率随着频率的提高而降低。例如，ifl0在OLS模型下日数据的套期保值比率为0.898011，15分钟数据的套期保值比率为0.786897，10分钟数据的套期保值比率为0.776643，5分钟数据的套期保值比率为0.647520，1分钟数据的套期保值比率为0.274535。

表2　沪深300股指期货在不同频率、不同套保模型下的套期保值比率

(2)在日数据下，期货ifl1在Diagnoal-VECH模型下的套期保值比率最大，为0.912637。期货ifl0、ifl2、ifl3在Diagnoal-BEKK模型下的套期保值比率值最大，分别是0.949224、0.909774、0.921736。

(3)在15分钟数据下，期货ifl0、ifl1、ifl2均在CCC-GARCH模型下的套期保值比率最大，分别是0.851104、0.863855、0.875807，期货ifl3在Diagnoal-BEKK模型下的套期保值比率值最大，为0.893392。

(4)在10分钟数据和5分钟数据下，期货ifl0、ifl1、ifl2、ifl3均在CCC-GARCH模型下的套期保值比率最大，对应的套期保值比率分别是0.837559、0.851649、0.861260、0.875518和0.687653、0.696298、0.703499、0.710858。

(5)在1分钟数据下，期货ifl0、ifl1、ifl2、ifl3均在DCC-GARCH模型下的套期保值比率最大，对应的套期保值比率分别是0.310982、0.306182、0.305635、0.333691。

(三)套期保值绩效综合分析

汇总沪深300股指期货不同频率、不同模型下的套期保值效果值，结果如表3 所示。

表3　沪深300股指期货在不同频率、不同模型下的套期保值效果值

续表3

对比表3中的套期保值效果值，主要基于小数点后前6位数的大小，若前六位数字相同，对比第7位或第8位数字，本表主要保留6位有效数字。根据表2可作出如下分析：

1. 同一套保组合在相同频率、不同模型下的套保效果分析

(1)组合A1即当月期货合约在日数据、15分钟数据、10分钟数据、5分钟数据和1分钟数据下的最优套保模型均为OLS模型，对应的套期保值效果值分别是0.891003、0.739301、0.698239、0.519110、0.152555。

(2)组合A2即下月期货合约基于日数据的最优套保模型为CCC-GARCH模型，对应的套保效果值为0.908908。15分钟、10分钟、5分钟数据下的最优套保模型为Diagonal-BEKK模型，对应的套保效果值分别是0.765553 、0.707751、0.531543。1分钟数据下的最优套保模型为B-VAR模型，对应的套保效果值为0.152554。

(3)组合A3即下季期货合约在日数据下的最优套保模型为CCC-GARCH模型，对应的套保效果值为0.898563。15分钟数据下的最优套保模型为DCC-GARCH模型，对应的套保效果值为0.767304。10分钟和1分钟数据的最优套保模型为OLS模型，对应的套保效果值分别为0.701329、0.151505。5分钟数据下的最优套保模型为Diagonal-BEKK模型，对应的套保效果值为0.531508。

(4)组合A4即隔季期货合约在日数据下的最优套保模型为CCC-GARCH模型，对应的套期保值效果值为0.892099。15分钟数据下的最优套保模型为DCC-GARCH模型，对应的套期保值效果值为0.765336。10分钟和5分钟数据下的最优套保模型为Diagonal-BEKK模型，对应的套保效果值分别是0.704853、0.534345。1分钟数据下的最优套期保值模型为OLS模型，对应的套保效果值为0.179049。

(5)通过对同一期货合约在相同模型、不同频率数据的套保效果进行对比，可以发现，同一期货合约在相同模型下，套保效果随频率的增大而降低。例如，当月期货合约在OLS模型下，日数据的套期保值效果值为0.891003，15分钟数据的套保效果值为0.739301，10分钟数据的套保效果值为0.698239，5分钟数据的套保效果值为0.519110，1分钟数据的套保效果值为0.152555。再如，期货ifl2在CCC-GARCH模型下，日数据的套期保值效果值为0.898563，15分钟数据的套保效果值为0.766015，10分钟的套保效果值为0.698137，5分钟数据的套保效果值为0.529478，1分钟数据的套保效果值为0.115623。

2. 不同期货合约在相同频率、相同模型下的套保效果分析

(1)在日数据下，4种期货合约中，下月期货合约ifl1在7个模型下的套期保值效果值均是最好的。

(2)在15分钟数据下，4种期货合约中，除了下月合约ifl1在Diagonal-VECH模型下的套保效果值，隔季期货合约ifl2在其他6种模型下的套期保值效果值均是最好的。

(3)在10分钟数据下，4种期货合约中，除了隔季期货合约ifl3在CCC-GARCH模型和DCC-GARCH模型下的套期保效果值外，下月期货ifl1合约在其他5种模型下的套期保值效果值均为最好的。

(4)在5分钟数据下，4种期货合约中，隔季期货合约ifl3在7种模型下的套期保值效果值均为最好的。

(5)在1分钟数据下，除了下月期货合约ifl1在Diagonal-BEKK模型下的套期保值效果值外，隔季期货合约ifl3在其他6种模型下的套期保值效果值最好。

(6)根据以上5点分析可知，与其他三种合约相比，当月期货合约ifl0在5种数据频率类型和7个套期保值模型下的套期保值效果值均不是最好的。这与市场的一般现象存在差异。一般情况下，当月期货合约与现货的价格较为接近，价格波动风险相对较小，它的套期保值效果应该优于下月、下季、隔季的期货合约。

(7)基于1分钟的数据，利用Diagonal-BEKK模型进行套期保值，期货ifl0、ifl2、ifl3的套期保值绩效均为负值，即套保组合的风险比未进行套保的现货风险更大，说明若采用不合适的套期保值模型和不合适的套保比率，期货不仅没有取得有效的保值效果，反而可能增大现货投资的风险。

3. 同一模型下相同期货合约在不同频率下的套保效果分析

(1)在同一模型下，相同期货合约的最优套期保值效果对应的数据频率均为日。例如，在静态模型OLS模型下，ifl0的日、15分钟、10分钟、5分钟、1分钟数据对应的套保绩效值为降序排列，依次分别是0.891003、0.739301、0.698239、0.519110、0.152555。在OLS模型下，ifl1、ifl2、ifl3合约也均为日数据下的套保效果最好。在其他模型下，上述结论不变。

(2)在日数据频率类型下，同一模型下的4种期货合约中，组合A2即下月期货合约的套期保值效果值最好。

(3)在3种静态模型和4种动态模型中，对现货和期货对数收益率进行套期保值，同一期货合约均是日数据的套保效果最好；其次是15分钟数据；第三是10分钟数据；第四是5分钟数据；第五是1分钟数据。因此，模型的套保效果随着套保数据频率的提高而降低，即日数据套保效果最好，而1分钟数据套保效果最差。故对现货和期货对数收益率进行套期保值应该采用低频数据下的日数据为宜。

(四)研究结论与不足

本文对沪深300股指期货的套保模型作了较为全面的分析，采用静态和动态共7种模型，研究了在低频日数据和4种高频数据环境下，4种不同到期期限期货合约的最优套保比率和套保效果，判断哪种套保模型是最优的套保模型。

本文与已有文献研究的主要区别：目前国内学者关于沪深300股指期货套期保值研究大多采用日数据作为研究对象，如魏宇等的研究只采用15分钟数据[28]，未就高频数据和低频数据的差异性作出分析。本文同时探讨了低频日数据和4种日内高频数据下的沪深300股指期货套期保值情况。通过实证分析发现：

(1)不论是使用静态模型还是动态模型，7种模型下的套期保值基本都可以降低套保组合的风险，套保效果随频率的增大而降低。即最优数据频率类型为日数据，日数据下套保组合收益率的方差相比现货收益率的方差降低了90%左右；其次是15分钟数据，15分钟数据下套保组合收益率的方差相比现货收益率的方差降低了75%左右；第三是10分钟数据，10分钟数据下套保组合收益率的方差相比现货收益率的方差降低了70%左右；第四是5分钟数据，5分钟数据下套保组合收益率的方差相比现货收益率的方差降低了53%左右；第五是1分钟数据，1分钟数据下套保组合收益率的方差相比现货收益率的方差降低了15%左右。

由于模型的套保效果随着套保数据频率的提高而降低，即日数据套保效果最好，而1分钟数据套保效果最差。故对现货和期货对数收益率进行套期保值应该采用低频数据下的日数据为宜。在最优数据频率类型即日数据下，当月期货合约的最优套期保值模型为OLS模型，最优套期保值比率为0.898011，套期保值效果值为0.891003；下月期货合约、下季期货合约、隔季期货合约的最优套期套期保值模型均为CCC-GARCH模型，对应的最优套期保值比率分别是0.907677、0.907221、0.919588，相应的最优套期保值效果值分别是0.908908、0.898563、0.892099。

(2)以往基于日频率数据研究期货套保问题的文献较多。Laws和Thompson针对英国股票市场的研究结果表明伦敦国际金融期货交易所的英国富时100指数(FTSE100)期货和英国富时250指数(FTSE250)期货可以为现货提供87%到98%的套保效率[29]；Kenourgios等对美国股指期货套保的研究证实标准普尔500指数(S&P500)期货的套保效果可以达到97%[30]； Wang和Hsu的研究发现亚洲市场的日经225指数(Nikkei225)期货、香港恒生股指期货和韩国KOSPI200指数期货的套保效率都达到90%以上。[31]本文的分析也证实了在日频率数据下，不论是哪种合约、哪种套保模型，得到的套保效率都高过89%，与上述三个文献的研究结果相同。魏宇等基于15分钟高频环境下的研究发现，沪深300股指期货的避险效率最高仅为70%左右。[32]本文则发现，当使用更高频率5分钟数据时，沪深300股指期货的套保效率又变得更差了，最高仅为56%左右。因此我们认为，当用股指期货对冲现货风险时，日数据下的套保效果反而要比日内高频数据下的套保效果好。

(3)从表3中，我们还可以看出，不管是日频率的低频数据还是4种高频数据，股指期货远期连续合约的套保效果要比近期合约的套保效果好。但传统的期货套保理论却是认为期货的近期合约交易相比远期合约而言应该更加活跃，越能反映现货价格的波动情况，因此期货近期合约的套保效率应该要高于远期合约。表3中的结论却与传统理论有较大差异。魏宇等研究认为：“其原因可能在于股指期货对于我国资本市场的各方参与者而言是新兴的交易工具。早期，由于规则的不熟悉和证监会的风险警示效应等原因，使得在沪深300 股指期货的交易中，更多存在的是投机者而非大量持有股票现货的券商等机构避险者。由于近期合约的成交量大，流动性更好，因此投机者更愿意参与其中，从而造成近期合约的价格信息失真，价格发现能力减弱。 对于券商等机构避险者来讲，由于其持有的股票现货头寸都有相对较长的持有期限，因此，远期合约更能满足其避险期间的需要。由于机构避险者更多地参与，从而可能导致远期合约的价格发现能力更强，其避险效率更高。”[33]

(4)实证表明，理论上较优的套期保值模型在实际表现中并不一定更优，动态模型不一定优于静态模型，如GARCH系列模型不一定优于OLS模型。投资者在做套期保值决策时，可以借鉴本文的实证研究结果，选择低频数据进行套期保值比率研究，同时结合自身的实际需要，选择对应的期货合约品种和套期保值模型，最后确定对应的套期保值比率。

本文通过实证研究发现，样本数据的频率类型对套期保值效果存在较大的影响，但还未分析数据频率类型对套期保值效果产生影响的深层次原因。此外，沪深300指数及其期货的套期保值效果受到诸多因素的影响，如市场摩擦，期货交易保证金、期货与现货价格间的波动关系和引导关系，资产收益的跳跃行为，高频数据的跳跃信息，期货套期保值的资金约束等等，而本文关于沪深300指数的套期保值模型的比较选择研究更多的是基于理想状态，即不考虑上述因素的影响，这与现实的金融市场情况还存在一定的距离。事实上有些因素的定量分析存在较大的难度，如市场摩擦因素，定量刻画市场摩擦因素的影响需要深厚的数学和计量的理论基础作为支撑，目前从市场摩擦的角度，定量研究市场模型下沪深300指数的套期保值模型的选择研究甚少，这可以成为学者以后研究的一个参考方向。

注释：

[1] 常 远：《中国期货市场的发展历程与背景分析》，《中国经济史研究》2007年第4期。

[2] 郑义彬：《中国股市系统风险估值研究》，《武汉理工大学学报》(信息与管理工程版)2007年第1期。

[3] 谢卫群：《股指期货不是“坏孩子”》，《人民日报》 2014年10月30日。

[4] 阳晓晖、伍海军：《多阶段系列展期套期保值研究》，《决策与统计》2007年第8期。

[5] 高 扬、郭晨凯：《我国股指期货套期保值效果的实证分析——基于下侧风险框架的分析》，《价格理论与实务》2011年第7期。

[6] 徐永春：《基于SVM技术的套期保值模型的实证分析》，《统计与决策》2013年第16期。

[7] 薛宏刚、张瑞敏、胡春萍等：《基于岭回归的套期保值方法》，《统计与决策》2012年第5期。

[8] 韩立岩：《基于已实现二阶矩预测的期货套期保值策略及对股指期货的应用》，《系统工程理论与实践》2012年第12期。

[9] 王继莹、郑耀威：《沪深300股指期货模型套期保值效率度量研究——基于沪深300ETF的实证分析》，《成都理工大学学报》2014年第6期。

[10] Ederington L. H.,“The hedging performance of the new futures markets”,TheJournalofFinance, vol.34,no.1(1979),pp. 157-170.

[11] Figlewski S., “Hedging with stock index futures: theory and application in a new market”,JournalofFuturesMarkets, vol.5,no.2(1985), pp. 183-199.

[12] Lee C. F., Bubnys E. L., Lin Y., “Stock index futures hedge ratios: Test on horizon effects and functional form”,AdvancesinFuturesandOptionsResearch,vol.2,no.3( 1987),pp. 291-311.

[13] Benet B. A., “Hedge period length and Ex‐ante futures hedging effectiveness: The case of foreign-exchange risk cross hedges”,JournalofFuturesMarkets, vol.12,no.2(1992), pp. 163-175.

[14] Cecchetti S. G., Cumby R. E., Figlewski S., “Estimation of the optimal futures hedge”,ReviewofEconomicsandStatistics, vol.70(1988),pp. 623-630.

[15] Baillie R. T., Myers R .J., “Bivariate GARCH estimation of the optimal commodity futures hedge”,JournalofAppliedEconometrics, vol.6,no.1(1991),pp. 109-124.

[16] Myers R. J. ,“Estimating time‐varying optimal hedge ratios on futures markets”,JournalofFuturesMarkets, vol.11,no.1(1991),pp. 39-53.

[17] Kroner K. F., Sultan J. ,“Time-varying distributions and dynamic hedging with foreign currency futures”,JournalofFinancialandQuantitativeAnalysis, vol.28,no.4(1993),pp. 535-551.

[18] Park T. H., Switzer L. N. ,“Bivariate GARCH estimation of the optimal hedge ratios for stock index futures: A note”,JournalofFuturesMarkets, vol.15,no.1(1995),pp. 61-67.

[19] Choudhry T. ,“Short-run deviations and optimal hedge ratio: evidence from stock futures”,JournalofMultinationalFinancialManagement, vol.13,no.2(2003),pp. 171-192.

[20] Lien D. ,“A note on the hedging effectiveness of GARCH models”,InternationalReviewofEconomics&Finance, vol.18,no.1(2009),pp. 110-112.

[21] 付剑茹、张宗成：《时变最优套期保值比估计及比较研究——基于卡尔曼滤波在状态空间模型中的应用》，《管理科学学报》 2011年第12期。

[22] 赵 莹：《套期保值应用浅析》，《商业会计》2013年第4期。

[23] Keynes J. M.，ATractonMonetaryReform，C.W，Macmillan, London,1923.

[24] Holdbrook Working，“New concepts concerning futures markets and prices”，AmericanEconomicReview,vol.52(1962),pp.431-459.

[25] 兰 鹏：《期货最优套期保值比率研究评述》，《财经理论研究》2013年第 1期。

[26] 易丹辉：《数据分析与EViews 应用》，北京：中国人民大学出版社，2012年,第263-269页。

[27] 崔百胜、伏开宝、万里欢：《中国股指期货动态保值率估计与套期保值绩效评价研究—基于非对称DCC MVGARCH模型的实证分析》，《金融管理研究》2013年第1期。

[28][32][33]魏 宇、赖晓东、余 江：《沪深300股指期货日内避险模型及效率研究》，《管理科学研究》2013年第3期。

[29] Laws J., Thompson J., “Hedging effectiveness of stock index futures”,EuropeanJournalofOperationalResearch, vol.163,no.1( 2005), pp. 177-191.

[30] Kenourgios D., Samitas A., Drosos P. ,“Hedge ratio estimation and hedging effectiveness: the case of the S&P 500 stock index futures contract”,InternationalJournalofRiskAssessmentandManagement, vol.9,no.1(2008),pp. 121-134.

[31] Wang J., Hsu H. ,“Hedge Ratio Stability and Hedging Effectiveness of Time‐Varying Hedge Ratios in Volatile Index Futures Markets: Evidence from the Asian Financial Crisis”,Asia-PacificJournalofFinancialStudies, vol.39,no.5(2010), pp. 659-686.

[责任编辑：黄艳林]

收稿日期：2015-11-26

基金项目：国家自然科学基金项目“基于已实现测量非参数方法的金融资产跳跃行为研究”(71171056)； 福州大学校科技启动基金“金融市场风险传染检验、传染效应分析及其传染渠道研究”(13SKQ02)。

作者简介：黄文彬， 女， 福建闽清人， 福州大学经济与管理学院副教授，硕士生导师，博士; 郑丽娟， 女， 福建漳平人， 福州大学经济与管理学院硕士研究生；林银瑞， 女， 福建莆田人， 福州大学经济与管理学院硕士研究生。

中图分类号：F830

文献标识码：A

文章编号：1002-3321(2016)03-0038-10