基于R软件的金融时间序列的预测分析

李瑞阁++庄元颖++李聪聪

摘 要 时间序列分析作为股票市场波动预测的重要工具，逐渐成为金融领域较常用的预测方法之一。本文利用R软件对上证综指和深证成指进行如下分析：根据上证指数收盘价的变动情况及其非平稳性和季节性特征建立包含季节因素的S-ARIMA模型，该模型较准确地描述和预测收盘价，实用性较强；对比剖析了上证综指和深证成指的收益率变动情况，针对其统计特性建立了相应的GARCH模型，得出了两指数收益率波动有时变性，簇集性，相关性等特征，模型拟合结果准确率较高。

【关键词】时间序列分析 股票波动预测 S-ARIMA模型 GARCH模型

宏观上，随着经济全球化的社会大背景趋势逐渐加强，股票由最初影响的局部性逐渐向当下的整体性转变。股票市场作为资本市场的核心，其动荡已不再仅仅影响部分企业的盈亏和部分人群的得失，波及面之广已经达到了空前的高度；微观上，股票跌宕起伏的变化与人们的日常生活包括幸福指数，经济状况越来越密切相关，据不完全统计，股市萎靡不振时，人们的幸福指数低且购买欲望低，内需减少，这足以说明股票市场对我国国民的影响力之大。合理正确的利用非平稳时间序列分析方法预测金融市场走势无论对国家的经济管控还是对个人经济状况的改善都具有指导意义。

1 基于季节性的ARIMA模型的上证指数收盘价的研究

指数收盘价指数是在交易所一日内最后一笔交易的成交价格，若当天没有成交，那么收盘价将采用最邻近的一次交易价格。因而可作为当日行情的参考指标，收盘价的走势和动态可用来预测未来的证券交易行情，投资者一般利用收盘价作为其投资的重要参考指标。影响收盘价变动的因素较多，收盘价的序列一般非平稳且具有某种趋势性，可采用理论ARIMA模型对其进行拟合预测。

案例：预测2016年4月底的收盘价。数据采用的是2001年12月11日也即我国加入世界经济贸易组织到2016年3月每月月底的收盘价格（去除掉非交易日的数据），共172个收盘价数据，利用这些数据进行ARIMA建模分析。

1.1 序列平稳性检验

利用时间序列趋势图，单位根检验，自相关（ACF）、偏自相关（PACF）图等检验时间序列平稳性，为识别时间序列的周期性及合适模型提供依据。利用R软件对原始数据做ADF检验，结果如下：ADF=-3.5557，p=0.03936>0.01，接受原假设，原始序列存在单位根且非平稳。通常情况下，对非平稳时间序列，差分可使其趋于平稳。对原始序列做一阶差分，差分后的序列进行ADF检验，结果如下：ADF=-4.5276，p=0.01<0.01，可拒绝原假设，即认为序列不存在单位根，说明差分后序列是平稳的。由差分后的时间序列自相关图一步截尾，偏自相关图拖尾，且偏自相关图可见差分后的时间序列具有某种季节性特征。由此可选用包含季节性因素的S-ARIMA模型预测上证指数收盘价较为合适。

1.2 建立S-ARIMA模型

经过两次差分后的序列已经几乎不再具有自相关性，且该模型可能只在滞后1和12阶上具有自相关的简单模型。对收盘价经一阶和季节差分后的样本自相关图进行分析，滞后1和12的自相关系数明显较大。考虑识别乘法季节ARIMA（0，1，1）*（0，1，1）[12]模型：

1.3 模型拟合

针对收盘价时间序列的模型，结果中给出极大似然估计出的参数值以及其标准误差0.0736，0.0978，所有的系数估计值都是高度显著的，因而所求模型：

1.4 诊断性检验及季节模型预测

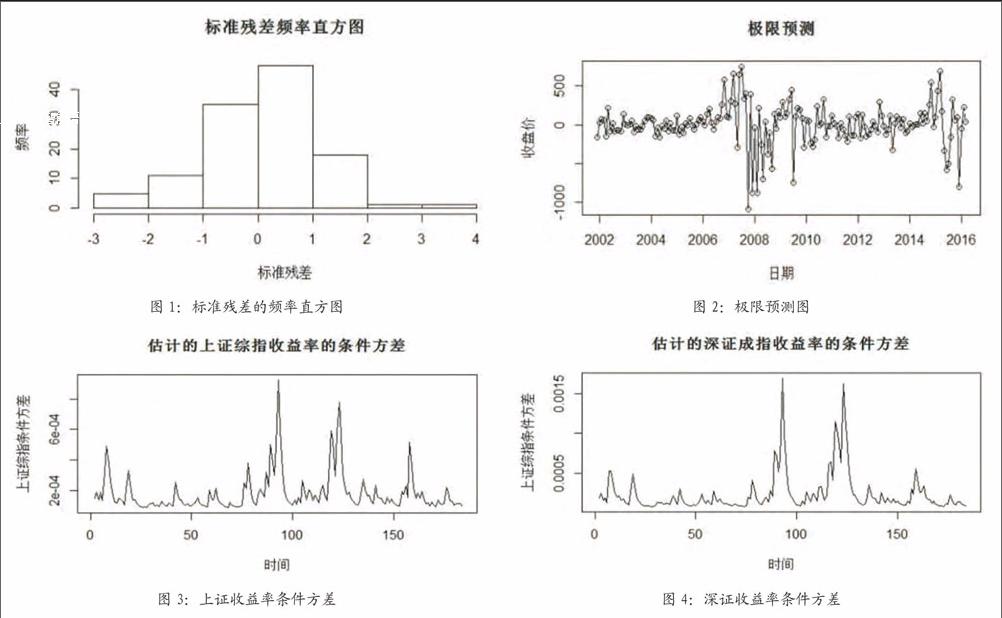
诊断模型的适应性，可借助残差序列来研究误差项的正态性问题。图1为根据残差序列绘制出的该模型的标准残差频率直方图，该图形状像“钟形”，表明模型的适应性良好。

图2的极限预测图可知，2016年4月份的月底收盘价较同年3月份会有所下降。

2 基于GARCH模型的沪深股市风险的波动性分析

在金融领域中，金融资产的条件方差通常具有异方差性，其波动的幅度通常也可作为度量资产风险的一种重要工具。如股票的收益率在波动幅度较大的时期内，相比较价格平稳时通常会有较大的异方差。以下通过建立条件异方差模型预测未来波动。

利用GARCH模型拟合上证综指和深圳成指的收益率序列，研究条件方差的波动对动态风险波动相关性并预测未来波动。样本数据采用1998年1月到2001年11月间所有的周收盘数据，两个指数的样本均为184个。

2.1 ARCH效应检验

设表示某金融资产在t时期的收盘价，那么收益率rt可表示为：

对于收益率序列的研究，只考虑其超过平均值的部分，记为。分别记上海综合指数和深圳成分指数周收盘价格超过平均值的部分为xt和yt。以下对xt和yt进行有关检验。

2.1.1 正态性检验

Jarque-Bera统计量可用来检验一组数据是否符合正态分布的统计量，通过计算偏度系数和峰度系数，建立J-B统计量对大样本进行渐近检验。J-B统计量可知上证综指、深成指J-B检验的P值均很小，拒绝原假设，认为样本不符合正态分布。

2.1.2 自相关检验

自相关图中能够看出时间序列相隔单位时期的观测值之间的相关关系。如果时间序列各个观测值之间没有相关性，那么自相关函数图位于标准差的2倍之间。对上证综指和深成指收益率及平方序列的自相关图进行分析：两指数的收益率序列不存在明显的相关性，收益率的平方序列却存在着直到4阶的自相关性，这说明两指数的收益率序列均存在ARCH效应。

2.1.3 异方差性的LM检验

对两个指数的收益率序列计算拉格朗日乘子LM统计量，两市12阶统计量的检验结果都表明收益率序列具有显著的条件异方差性。

2.2 拟合GARCH模型

对上证综指和深证成指的收益率时间序列进行模型拟合，得到参数显著，分别为4.558e-05，2.816e-01，4.682e-01并且给出了模型残差序列的Box-Ljung检验结果，P值为0.7042>0.05，接受残差序列服从正态分布的原假设，同样残差平方的序列Box-Ljung检验P值0.9681>0.05，接受残差平方序列服从正态分布的原假设。说明模型拟合较优。所以，上证综指收益率时间序列的模型可表示如下：

同理可得深证成指收益率时间序列的模型为：

2.3 模型诊断

残差分析可诊断模型适应性。一般地，若模型被正确识别，则残差序列独立同正态分布。残差的正态性检验通过QQ图检验。事实上，独立同分布序列的非零阶滞后的样本自相关系数也往往呈现独立零均值，方差为1/n正态分布，基于收益率数据不相关前提，相同阶数的GARCH模型生成的残差也是独立同正态分布的，因而上述模型被正确识别。

2.4 风险波动预测

利用所建模型对上证综指和深证成指进行条件方差的多期预测，风险波动预测如图3、图4。

2.5 风险波动（条件方差）的特征分析

从以上条件方差波动预测图可见该样本期内沪深股市的风险波动具有以下特点：

2.5.1 时变性

两指数方差的波动均随时间变化而变化，且变化比较剧烈，其最大值与最小值相差均为十倍以上。这说明沪深股市明显处于波动幅度比较大的时期，具有明显的波动时变性。

2.5.2 簇集性

两指数的方差序列均具有明显的簇集性特征，即波动幅度大的往往在某一时期内，而其余时期波动幅度都比较小。

2.5.3 相关性

对比两方差序列图，可见在同一时期内，两图波动幅度往往相似。即其中一个指数的方差波动总是紧随着另一个指数的上升而上升，下降而下降。

3 研究结果比较

ARIMA是非平稳时间序列，它是条件均值结构模型；GARCH模型存在异方差时的条件方差结构模型。一般地，若某时间序列满足ARIMA模型，任意给定步长的向前预测，其条件方差总为常数。实际问题中，条件方差往往具有时变性，条件方差本身也是一个随机过程，即条件方差过程。ARIMA模型主要研究基于现在和过去的数据预测未来的数据，而GARCH模型主要研究基于现在和过去的数据预测未来的波动。

参考文献

[1]BOX G，JENKINSG.Time series analysis：Forcasting and control（rev.ed.）Holden-Day.San Francisco，1976.

[2]尤作军.时间序列分析在股票中的研究与应用[D].沈阳工业大学，2014.

[3]王振龙，胡永宏.应用时间序列分析[M].北京：科学出版社，2007：3-26.

[4]商安娜.基于SARIMA的电梯交通流递归预测方法的研究[D].天津：天津大学，2007.

[5]ENGLE R.Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation，Econometrica，1982，50（04）：987-1007.

[6]Jonathan D.Cryer，Kung-Silk Chan.Time Series Analysis with APPlications inR（Second Edition）.潘红宇译.时间序列分析及应用（第二版）[M].北京：机械工业出版社，2011，1：218-221.

[7]张锋.中国饲料加工业产业组织研究[D].石河子：石河子大学，2013.

[8]黄欣.光测设备捕获能力检验中目标特性标校[D].中国科学院研究生院（长春光学精密机械与物理研究所），2015.

[9]周俊妍.我国股票市场波动和股票溢价之间的关联机制[D].长春：吉林大学（硕士论文），2009.

[10]林宇.中国股市与国际股市的极值风险传导效应研究[D].成都：成都理工大学，2008.

作者简介

李瑞阁（1964-），女。硕士学位。现为南阳理工学院数学与统计学院教授。主要研究方向为时间序列分析，多元统计等。

作者单位

南阳理工学院数学与统计学院 河南省南阳市 473004