肋环型顶盖屈曲影响因素分析及稳定承载力计算

贾冬云，王　涛，杨 军（安徽工业大学建筑工程学院，安徽马鞍山243032）

肋环型顶盖屈曲影响因素分析及稳定承载力计算

贾冬云，王涛，杨 军
（安徽工业大学建筑工程学院，安徽马鞍山243032）

选取36种结构形式的基本模型，采用弧长法对以第一阶屈曲模态作为初始形态的结构进行非线性屈曲分析，探讨边界条件、初始缺陷、矢跨比和截面尺寸对结构屈曲性能的影响。通过分析曲率半径、等效薄膜厚度和等效弯曲厚度与临界屈曲荷载之间的量化关系，采用最小二乘法拟合肋环型加劲浅球壳临界失稳式，分析并选取安全系数，得到稳定容许承载力标准值计算式。

气柜顶盖；肋环形加劲浅球壳；临界屈曲荷载；有效厚度；稳定承载力

大容量的钢结构储罐随钢铁厂副产二次能源合理利用的要求应运而生。然而，在实际应用中，大型储罐的顶盖稳定性理论研究欠缺，指导设计的相关规范较少，致使在已建成的储罐中，时有顶盖失稳的状况发生［1-2］。环肋形加劲浅球壳是各种储罐拱顶常采用的形式之一，因其用钢量较省、减轻了顶盖的荷载而倍受青睐。此类结构的整体稳定性问题仍是研究热点。采用有限元模型的简化和计算模式使问题的研究有了一定进展。如加大主梁在铺板面内的抗弯模量建立简化模型，以一阶极限荷载值作为结构发生失稳的临界荷载值［3］；将40倍到60倍铺板厚度的板宽计入次肋刚度的计算屈曲荷载的模型［4］；考虑铺板局部屈曲后强度，利用几何非线性弧长法进行全过程分析，研究结构失稳的原因和屈曲过程［5］。本课题以华东某10万m3一段橡胶膜密封气柜的顶盖为背景，建立36种结构模型，采用有限元模拟与理论分析相结合的方法，研究矢跨比、边界条件、初始缺陷等因素对加劲壳的屈曲性能的影响，确定有效薄膜厚度和弯曲厚度的取值，得出相应设计参数，拟合稳定容许承载力计算式。

1　有限元模型的选取与计算

1.1顶盖结构

华东某10万m3肋环型气柜的顶盖由中心环梁、边环梁、经向主肋、环向主肋、经向次肋、顶板组成的浅球形加劲球壳（图1）。经向主肋的数量为32根，截面为槽钢［18a；环向主肋为9道，沿经向圆弧等距离分布，外侧4道的截面为槽钢［18a，内侧5道的截面为槽钢［14a。中心环梁的截面为槽钢［18a。经向主肋与环向主肋构成的骨架构造单元中设有经向次肋，截面为L75×6角钢，数量由外环带向内环带逐步减少；盖板采用4 mm钢板。其他模型几何参数如下：球壳曲率半径为80 810 mm，矢高为6 210 mm，跨度为62 132 mm，矢跨比为1/10，中心角为22.60°，中心环梁半径为1 200 mm。

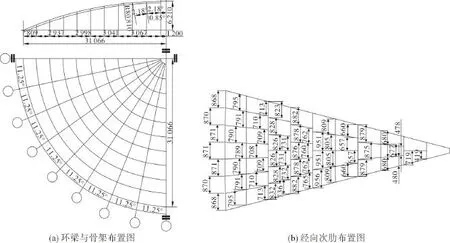
图1　顶盖结构实例示意图Fig.1 Roof structure sketch

1.2有限元模型的选取

根据工程实例，本研究模型保持结构的跨度、主次肋的分布形式和数目不变，改变模型的矢跨比和构件的截面尺寸，得到以矢跨比分组的36种结构形式的基本模型，见表1。其中A，B，C，D组分别对应矢跨比为1/9，1/10，1/11，1/12，即曲率半径为73 384，80 810，88 230，95 975 mm的模型。经向次肋均为角钢L75×6。

1.3有限元模型的临界屈曲荷载计算

在对上述基本模型进行有限元分析的过程中，每个模型的边界条件分别取为固接和铰接，结构的初始缺陷分别取L/200，L/300，L/500，L/800，L/1 000。参照一致缺陷模态法［6-8］，先进行特征值屈曲分析，得到第一阶屈曲模态，以第一阶屈曲模态作为结构的初始形态，定义初始缺陷值；然后采用弧长法对该结构进行非线性屈曲分析，得到顶盖结构的整体失稳时临界屈曲荷载的计算结果。选取经向主肋的竖向位移最大的节点进行研究，以1/300跨度为初始缺陷值、边界条件为固接和铰接所计算的屈曲临界荷载值分别为qcr，F和qcr，P。将36种模型的屈曲临界荷载值列入表1。其中，模型A1初始缺陷为L/300的固接和铰接的屈曲变形图见图2。

表1　36种模型的L/300初始缺陷的屈曲临界荷载Tab.1 Buckling loads of 36 models with L/300 initial imperfection

图2　L/300初始缺陷的A1模型屈曲变形图Fig.2 Buckling deformation of modelA1 with L/300 initial imperfection

2　肋环型加劲浅球壳的屈曲影响因素分析

2.1边界条件

气柜顶盖边缘设有T型截面的边环梁，经向主肋、次肋和板与边环梁可靠连接。在肋环型加劲浅球壳模型的分析过程中，采用固接和铰接两种边界条件来计算顶盖屈曲临界荷载，对不同矢跨比结构的两种计算结果进行比较，见图3。

通过对比可知，固接时的屈曲荷载与铰接时的屈曲荷载最大平均偏差率约为7.1%，因此固接和铰接时结构的屈曲荷载值基本持平。分析其原因在于：大跨度的壳状结构，支座之间的距离较大，临界屈曲波长较小，它仍以特定的临界屈曲波长发生失稳［9］，临界屈曲荷载与塌陷区域处的截面属性直接相关，与远处的支座形式间接相关。因此，固接和铰接形式的支座对屈曲临界荷载的影响较小。

2.2初始缺陷

鉴于边界条件对屈曲荷载影响较小，故选取固接情况下，初始缺陷值分别为结构跨度L的1/1 000，1/800，1/500，1/300和1/200等5种的计算结果，绘制各组结构的屈曲临界荷载随初始缺陷变化的关系见图4。

图3　不同矢跨比的固接和铰接的结构屈曲荷载比较Fig.3 Comparison of buckling loads between fixed and pinned boundary with different rise span ratio

图4　各组结构屈曲节点的临界荷载随初始缺陷变化Fig.4 Buckling loads variation with initial imperfection at buckling nodes for each group

由图4可知：随着结构初始缺陷的增大，结构的屈曲临界荷载呈现出减小的趋势；但是总体上，初始缺陷的变化对结构的屈曲临界荷载值的影响较小；当初始缺陷超过L/300后有一定影响，屈曲荷载的偏差率增大。因此，L/300的初始缺陷可作为结构安装误差的限定值，以控制初始缺陷对结构屈曲荷载的影响。

2.3矢跨比和截面尺寸

基于上述分析结论，边界条件和初始缺陷对模型整体失稳时的屈曲荷载值影响较小，按矢跨比分类，选取在边界条件为固结、初始缺陷为L/300时的模型非线性屈曲计算结果，绘制各组结构屈曲节点的荷载-位移变化曲线图5。

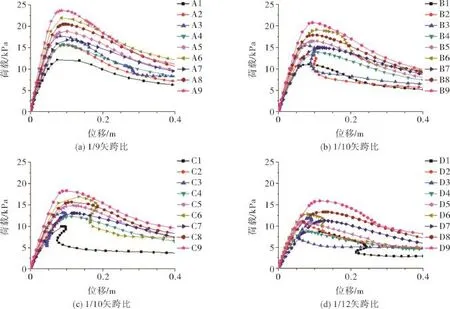
图5　不同矢跨比的结构屈曲节点的荷载-位移曲线Fig.5 Load-displacement curves at buckling nodes of structures with different rise span ratio

由图5可知：结构失稳时，随矢跨比的降低，最大变形值增大，最大临界屈曲荷载值降低；结构的临界荷载值随主肋截面尺寸的增大而增大；在曲线的直线上升段，结构的位移值很小，表明结构处于弹性工作阶段，其刚度较大；达到极值点之前，结构的位移增值比荷载的增值渐渐加大，表明结构处于弹塑性工作阶段，虽然刚度逐渐退化，但仍处于稳定平衡状态；曲线下降段，维持平衡的荷载减小，结构变形加快，表明结构的刚度矩阵为非正定，结构的刚度退化明显，呈现脆性破坏特征，处于不稳定平衡状态，最终结构出现较大范围塌陷，发生整体失稳。因此，顶盖结构的失稳模态为极值点失稳，该极限点对应的荷载可视为结构整体失稳的临界屈曲荷载值，即稳定极限承载力。

3　稳定容许承载力的计算公式拟合

对于各向同性的球面壳状结构，引入分离刚度的概念，以等效弯曲厚度tB和等效薄膜厚度tm分别用于描述构件的惯性矩和面积对结构稳定承载力的贡献，弹性临界法向荷载表示为［10］

式中：C为系数；E为钢材的弹性模量；R为球壳的曲率半径。

3.1肋环形加劲浅球壳的等效弯曲厚度和等效薄膜厚度

肋环形加劲浅球壳的每个计算单元在经向和环向的截面属性不同。由图6可以得出一个计算单元（阴影部分）经向和环向的组合截面属性：lφ，lθ是经向和环向的长度；Aφ，Aθ是经向和环向的截面面积；Iφ，Iθ是经向和环向的截面惯性矩。

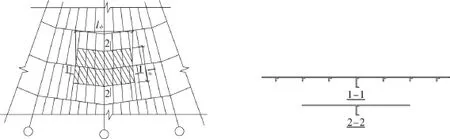
图6　经向和环向的组合截面示意图Fig.6 Sketches of compound section at longitudinal and circumferential ribs

由于肋环加劲球壳的薄膜厚度和弯曲厚度在经向和环向是不同的，借鉴文献［11-12］的等效厚度拟合方式，取顶板、经向和环向的计算厚度在组合截面的权重均为1，得到相应的等效厚度：

3.2稳定承载力公式的拟合

针对36种基本模型的计算结果，选取初始缺陷为L/300、边界条件为固接的临界屈曲荷载计算结果（见表1），分析等效效薄膜厚度和等弯曲厚度与临界屈曲荷载的量化关系，进而拟合肋环型加劲浅球壳整体稳定性的极限承载力计算公式。

参照式（1），可拟定肋环型加劲浅球壳的稳定极限承载力表达式为

式中：α为系数；β为等效薄膜厚度的指数系数；γ为等效弯曲厚度的指数系数。

因为式（4）为非线性多元函数，根据表1中的有限元计算结果，qcr，F和该位移最大点所在计算单元的截面属性R，tm和tB计算值，引入MATLAB中的基于Gauss-Newton算法的最小二乘拟合函数nlinfit函数，对式（4）进行拟合，得出未知系数α，β和γ，从而得到稳定极限承载力计算式为

结构的极限承载力是结构完全破坏前所能承受的外荷载的最大能力。具有一定安全度和不引起超出使用范围的变形的外荷载是容许承载力，它兼顾强度和变形两方面的要求。因此，以结构的极限荷载作为容许承载力是不安全的，安全系数K的选择至关重要［13-14］。

针对本文所分析的肋环形加劲浅球壳结构的安全系数K值确定，应该考虑以下因素：以系数k1=1.4考虑外部作用（施工荷载和半跨荷载）的不确定性可能带来的不利影响因素；以系数k2=1.4考虑结构抗力的不确定性（如部分构件的部分截面在结构达到临界点前进入弹塑性状态，呈现脆性破坏特征）可能带来的不利影响因素；以系数k3=1.3来考虑结构工作条件中的其他不利因素（如低温环境）可能带来的不利影响因素；以系数k4=2来考虑结构稳定性分析中可能的不精确性（如网格尺寸偏大造成模型刚度增大、板和肋的截面刚度相差很大造成变形不协调）可能带来的不利影响因素。因此，对于按弹塑性全过程分析求得的稳定极限承载力，其安全系数K应取为1.4×1.4×1.3×2≈5。

将稳定极限承载力计算式（5）除以安全系数5，则得肋环形加劲浅球壳结构的稳定容许承载力标准值简化算式

4　结　论

1）边界条件采用固接与铰接对顶盖结构整体失稳的临界屈曲荷载值影响较小。

2）初始缺陷的变化对结构的屈曲临界荷载值的有一定影响，但影响较小。L/300的初始缺陷可作为结构安装误差的限定值，以控制初始缺陷对结构屈曲荷载的影响。

3）矢跨比和截面尺寸对临界屈曲荷载值影响明显。临界屈曲荷载值随矢跨比的降低而降低，随截面尺寸的增大而增大。

4）初步设计时，式（6）可以用来估算肋环型加劲浅球壳的容许承载力。

［1］李静波.尺寸超规范的带肋拱顶油罐的设计［J］.山东化工，2007，36（6）:23-24.

［2］黄文霞.渣油罐拱顶失稳分析及修复探讨［J］.石油化工设备技术，2008，29（1）:25-28.

［3］周伟.新型煤气柜的强度和稳定性分析［D］.重庆：重庆大学，2004.

［4］常安果，周圣凯，龚宗宜.环肋型球面壳煤气柜顶盖稳定分析［J］.钢结构，2012，7（27）:1-10.

［5］黄斌，毛文筠.大型煤气柜顶盖的几何非线性全过程分析［J］.武汉理工大学学报，2006，28（4）:63-66.

［6］陈昕，沈世钊.网壳结构的几何非线性分析［J］.土木工程学报，1990，23（3）:47-57.

［7］邓长根，徐忠根.缺陷结构稳定分析的一致缺陷模态近似法［J］.钢结构，2012（增刊）:209-216.

［8］陈绍蕃.钢结构稳定设计指南［M］.3版.北京：中国建筑工业出版社，2013.

［9］BUCHER K P.Buckling of Shell and Shell-like Structures［M］.Columbia:Missouri，1973.

［10］ZIEMIAN R D.Guide to Stability Design Criteria for Metal Structures［M］.New Jersey:John Wiley&Sons，2010.

［11］中国石油天然气集团公司.立式圆筒形钢制焊接油罐设计规范：GB50341—2014［S］.北京：中国计划出版社，2014.

［12］中国建筑科学研究院.钢筋混凝土薄壳结构设计规程：JGJ22—2012［S］.北京：中国建筑工业出版社，2012.

［13］中国建筑科学研究院.网壳技术规程：JGJ61—2003［S］.北京：中国建筑工业出版社，2003.

［14］中国建筑科学研究院.空间网格结构技术规程：JGJ7—2010［S］.北京：中国建筑工业出版社，2010.

责任编辑：丁吉海

Buckle Effect FactorsAnalysis and Stability Bearing Capacity Check of Rib Ring Stiffened Roof

JIADongyun，WANG Tao，YANG Jun
（School of Civil Engineering andArchitecture，Anhui University of Technology，Ma'anshan 243032，China）

Selecting 36 the basic models，the arc length method is used to the nonlinear buckling analysis of the structure with the first order buckling mode as the initial form.The influence of boundary condition，initial defect，rise span ratio and section size on the structure buckling performance is investigated.Through the quantitative analysis of the relationship between the radius of curvature，the equivalent membrane thickness，the equivalent bending thickness and the critical buckling load，fitting the buckling critical formula by using the least square method，analyzing and selecting the safety factor，the calculation formula of characteristic value of stability allowable bearing capacity is obtained.

gasholder roof；rib ring stiffened shallow spherical shell；critical buckling load；equivalent thickness；stability bearing capacity

TU392.6

A

10.3969/j.issn.1671-7872.2016.01.016

1671-7872（2016）-01-0076-07

2015-09-24

安徽工业大学研究生创新研究基金项目（2015053）

贾冬云（1968-），女，安徽合肥人，博士，副教授，主要研究方向为钢结构及组合结构。